2.6直角三角形 同步练习(含答案)2025-2026学年浙教版数学八年级上册
文档属性
| 名称 | 2.6直角三角形 同步练习(含答案)2025-2026学年浙教版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 183.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 20:59:47 | ||
图片预览




文档简介
2.6直角三角形
第 1课时直角三角形的性质
A 掌握基本知识
1.设直角三角形中一个锐角为 另一个锐角为 y°,则y与x的数量关系为 ( )
A. y=180+x B. y=180-x
C. y=90+x D. y=90-x
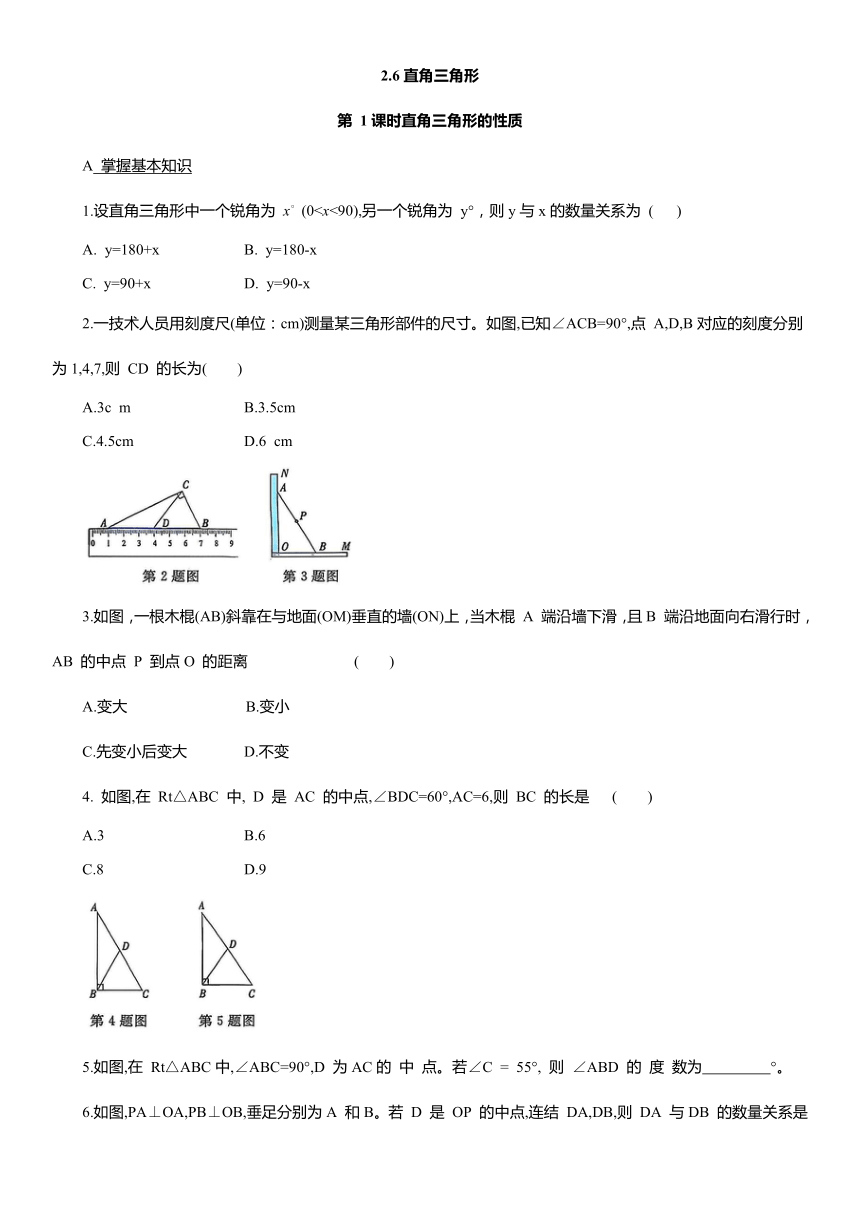
2.一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸。如图,已知∠ACB=90°,点 A,D,B对应的刻度分别为1,4,7,则 CD 的长为( )
A.3c m B.3.5cm
C.4.5cm D.6 cm
3.如图,一根木棍(AB)斜靠在与地面(OM)垂直的墙(ON)上,当木棍 A 端沿墙下滑,且B 端沿地面向右滑行时,AB 的中点 P 到点O 的距离 ( )
A.变大 B.变小
C.先变小后变大 D.不变
4. 如图,在 Rt△ABC 中, D 是 AC 的中点,∠BDC=60°,AC=6,则 BC 的长是 ( )
A.3 B.6
C.8 D.9
5.如图,在 Rt△ABC中,∠ABC=90°,D 为AC的 中 点。若∠C = 55°, 则 ∠ABD 的 度 数为 °。
6.如图,PA⊥OA,PB⊥OB,垂足分别为A 和B。若 D 是 OP 的中点,连结 DA,DB,则 DA 与DB 的数量关系是 。
7.若直角三角形斜边上的高线长与中线长分别为 5 和6,则它的面积为 。
8.如图,在 Rt△ABC中,∠ACB=90°,将边 BC沿斜边上的中线CD 折叠到B'C处。若∠B=50°,则
9.求证:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
已知:如图,在 Rt△ABC中,∠A=30°,∠ACB=90°。
求证:
(1)请用两种方法完成证明。
(2)这个命题的逆命题是 命题(填“真”或“假”)。
提升关键能力
10.如图,在△ABC 中,若 AB=AC=4,∠BAC=150°,则 S△ABC的值为 ( )
A.2 B.3
C.4 D.6
11.如图,在△ABC中,AB=AC,∠BAC=120°,EF 为AB 的垂直平分线,交 AB 于点 E,交BC于点F。若 BF=5,则 FC的长为( )
A.5 B.7
C.10 D.12
12.如图,在 Rt△ABC 中,∠ACB=90°,D 为 AB的中点,DE⊥AC 于点 E。若∠A=30°,DE=4 cm,则AB= cm,CD= cm。
13.如图,在△ABC中,∠C=90°,AB=10,AC=8,BC=6,线段 DE的两个端点 D,E分别在边AC,BC上滑动,且 DE=4。若 M,N 分别是DE,AB 的中点,则MN的最小值为 。
14.如图,在 Rt△ABC中,∠ACB=90°,CD 是AB 边上的中线,DE⊥AB 于点 D,交 AC 于点E。求证:∠AED=∠DCB。
15.如图,△ABC为等边三角形,BD 是AC 边上的高线,延长 BC至点 E,使 CE=CD。
(1)求证:DB=DE。
(2)过点 D 作DF⊥BE,垂足为 F。若CF=3,求△ABC的周长。
发展核心素养
16.[推理能力]如图,在△ABC中,AB=AC,D,E 分别是AB,BC的中点,连结AE,在 AE上取点F,使得 EF=AD,连结 DF 并延长,交AC于点G。
(1)当∠BAC=60°时,求∠AGD 的度数。
(2)设∠BAC=α,∠AGD=β,探究α,β之间的关系。
第 2课时 直角三角形的判定
A掌握基本知识
1.在具备下列条件的△ABC 中,不属于直角三角形的是 ( )
A.∠A+∠B=∠C
B.∠A-∠B=∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=2∠C
2.如果三角形的一个顶点是它的三条高线的交点,那么这个三角形是 ( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
3.如图,在四边形 ABCD 中,AB ∥DC。若∠BAD 的平分线与∠CDA 的平分线相交于点 E,则△AED 的形状一定为 ( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
4.如图,在△ABC 中,AB=AC=6,AD 是角平分线,BE 是中线,则 DE 的长为 ( )
A.3 B.4
C.5 D.6
5.如图,在△ABC 中,CD 是 AB 边上的高线。若∠DCB=∠A,则∠BCA= °。
6.在△ABC中,若 则此三角形是 三角形。
7.如图,CE⊥AD,垂足为 E,∠A=∠C。求证:△ABD 是直角三角形。
8.如图,AD,BF分别是△ABC 的高线与角平分线,BF,AD 相交于点 E,∠1=∠2。求证:△ABC是直角三角形。
9.我们知道定理:直角三角形斜边上的中线等于斜边的一半。请思考:上述定理的逆命题成立吗 若成立,写出其逆命题,并证明;若不成立,试说明理由。
(1)逆命题是: 。
(2)已知: 。
求证: 。
证明:
B提升关键能力
10.如图,在△ABC中,D 是 BC 边上的一点,AD=AB,E,F分别是BD,AC 的中点。若 AC=8,则 EF 的长为 。
11.已知:如图,BD⊥AC,垂足为E,△ABE的中线 EF 的反向延长线交 CD 于点 G,∠B=∠C。
(1)求证:EG是△CDE 的高线。
(2)若 EG 是△CDE 的中线,判断△ABE 的形状,并说明理由。
12.在△ABC中,∠ABC=45°,AD⊥BC,垂足为D,BE⊥AC,垂足为 E,直线 AD 交直线 BE于点 F,连结CF。
(1)如图1,若∠BAC 是锐角,求证:△CDF是等腰直角三角形。
(2)如图2,若∠BAC是钝角,则(1)中的结论是否仍成立 请说明理由。
发展核心素养
13.[模型观念]如图,在△ABC 中,∠C=90°,∠A=30°,AB=4 cm。动点 P,Q分别从A,B两点同时出发,各在 AB,BC 边上匀速移动,它们的速度分别为Vp =2 cm/s,vQ =1 cm/s。当点 P 到达点 B 时,P,Q 两点同时停止运动,设点 P 运动的时间为t(s)。
(1)当t为何值时,△PBQ是等边三角形
(2)当 t为何值时,△PBQ是直角三角形
2.6直角三角形
第1课时 直角三角形的性质
1. D 2. A 3. D 4. A 5.35 6. DA=DB 7.30
8.10 9.(1)略 (2)真 10. C 11. C 12.16 8 13.3
14.略 15.(1)略 (2)36 16.(1)75°
第2课时 直角三角形的判定
1. D 2. B 3. B 4. A 5.90 6.等腰直角 7.略 8.略
9.(1)如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形
(2)在△ABC 中,CD 是 AB 边的中线,且 △ABC是直角三角形,证明略
10.4
11.(1)略 (2)△ABE是等腰直角三角形。理由略
12.(1)略 (2)(1)中的结论仍成立。理由略
13.(1) (2)1或
第 1课时直角三角形的性质
A 掌握基本知识
1.设直角三角形中一个锐角为 另一个锐角为 y°,则y与x的数量关系为 ( )
A. y=180+x B. y=180-x
C. y=90+x D. y=90-x
2.一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸。如图,已知∠ACB=90°,点 A,D,B对应的刻度分别为1,4,7,则 CD 的长为( )
A.3c m B.3.5cm
C.4.5cm D.6 cm
3.如图,一根木棍(AB)斜靠在与地面(OM)垂直的墙(ON)上,当木棍 A 端沿墙下滑,且B 端沿地面向右滑行时,AB 的中点 P 到点O 的距离 ( )
A.变大 B.变小
C.先变小后变大 D.不变
4. 如图,在 Rt△ABC 中, D 是 AC 的中点,∠BDC=60°,AC=6,则 BC 的长是 ( )
A.3 B.6
C.8 D.9
5.如图,在 Rt△ABC中,∠ABC=90°,D 为AC的 中 点。若∠C = 55°, 则 ∠ABD 的 度 数为 °。
6.如图,PA⊥OA,PB⊥OB,垂足分别为A 和B。若 D 是 OP 的中点,连结 DA,DB,则 DA 与DB 的数量关系是 。
7.若直角三角形斜边上的高线长与中线长分别为 5 和6,则它的面积为 。
8.如图,在 Rt△ABC中,∠ACB=90°,将边 BC沿斜边上的中线CD 折叠到B'C处。若∠B=50°,则
9.求证:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
已知:如图,在 Rt△ABC中,∠A=30°,∠ACB=90°。
求证:
(1)请用两种方法完成证明。
(2)这个命题的逆命题是 命题(填“真”或“假”)。
提升关键能力
10.如图,在△ABC 中,若 AB=AC=4,∠BAC=150°,则 S△ABC的值为 ( )
A.2 B.3
C.4 D.6
11.如图,在△ABC中,AB=AC,∠BAC=120°,EF 为AB 的垂直平分线,交 AB 于点 E,交BC于点F。若 BF=5,则 FC的长为( )
A.5 B.7
C.10 D.12
12.如图,在 Rt△ABC 中,∠ACB=90°,D 为 AB的中点,DE⊥AC 于点 E。若∠A=30°,DE=4 cm,则AB= cm,CD= cm。
13.如图,在△ABC中,∠C=90°,AB=10,AC=8,BC=6,线段 DE的两个端点 D,E分别在边AC,BC上滑动,且 DE=4。若 M,N 分别是DE,AB 的中点,则MN的最小值为 。
14.如图,在 Rt△ABC中,∠ACB=90°,CD 是AB 边上的中线,DE⊥AB 于点 D,交 AC 于点E。求证:∠AED=∠DCB。
15.如图,△ABC为等边三角形,BD 是AC 边上的高线,延长 BC至点 E,使 CE=CD。
(1)求证:DB=DE。
(2)过点 D 作DF⊥BE,垂足为 F。若CF=3,求△ABC的周长。
发展核心素养
16.[推理能力]如图,在△ABC中,AB=AC,D,E 分别是AB,BC的中点,连结AE,在 AE上取点F,使得 EF=AD,连结 DF 并延长,交AC于点G。
(1)当∠BAC=60°时,求∠AGD 的度数。
(2)设∠BAC=α,∠AGD=β,探究α,β之间的关系。
第 2课时 直角三角形的判定
A掌握基本知识
1.在具备下列条件的△ABC 中,不属于直角三角形的是 ( )
A.∠A+∠B=∠C
B.∠A-∠B=∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=2∠C
2.如果三角形的一个顶点是它的三条高线的交点,那么这个三角形是 ( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
3.如图,在四边形 ABCD 中,AB ∥DC。若∠BAD 的平分线与∠CDA 的平分线相交于点 E,则△AED 的形状一定为 ( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
4.如图,在△ABC 中,AB=AC=6,AD 是角平分线,BE 是中线,则 DE 的长为 ( )
A.3 B.4
C.5 D.6
5.如图,在△ABC 中,CD 是 AB 边上的高线。若∠DCB=∠A,则∠BCA= °。
6.在△ABC中,若 则此三角形是 三角形。
7.如图,CE⊥AD,垂足为 E,∠A=∠C。求证:△ABD 是直角三角形。
8.如图,AD,BF分别是△ABC 的高线与角平分线,BF,AD 相交于点 E,∠1=∠2。求证:△ABC是直角三角形。
9.我们知道定理:直角三角形斜边上的中线等于斜边的一半。请思考:上述定理的逆命题成立吗 若成立,写出其逆命题,并证明;若不成立,试说明理由。
(1)逆命题是: 。
(2)已知: 。
求证: 。
证明:
B提升关键能力
10.如图,在△ABC中,D 是 BC 边上的一点,AD=AB,E,F分别是BD,AC 的中点。若 AC=8,则 EF 的长为 。
11.已知:如图,BD⊥AC,垂足为E,△ABE的中线 EF 的反向延长线交 CD 于点 G,∠B=∠C。
(1)求证:EG是△CDE 的高线。
(2)若 EG 是△CDE 的中线,判断△ABE 的形状,并说明理由。
12.在△ABC中,∠ABC=45°,AD⊥BC,垂足为D,BE⊥AC,垂足为 E,直线 AD 交直线 BE于点 F,连结CF。
(1)如图1,若∠BAC 是锐角,求证:△CDF是等腰直角三角形。
(2)如图2,若∠BAC是钝角,则(1)中的结论是否仍成立 请说明理由。
发展核心素养
13.[模型观念]如图,在△ABC 中,∠C=90°,∠A=30°,AB=4 cm。动点 P,Q分别从A,B两点同时出发,各在 AB,BC 边上匀速移动,它们的速度分别为Vp =2 cm/s,vQ =1 cm/s。当点 P 到达点 B 时,P,Q 两点同时停止运动,设点 P 运动的时间为t(s)。
(1)当t为何值时,△PBQ是等边三角形
(2)当 t为何值时,△PBQ是直角三角形
2.6直角三角形
第1课时 直角三角形的性质
1. D 2. A 3. D 4. A 5.35 6. DA=DB 7.30
8.10 9.(1)略 (2)真 10. C 11. C 12.16 8 13.3
14.略 15.(1)略 (2)36 16.(1)75°
第2课时 直角三角形的判定
1. D 2. B 3. B 4. A 5.90 6.等腰直角 7.略 8.略
9.(1)如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形
(2)在△ABC 中,CD 是 AB 边的中线,且 △ABC是直角三角形,证明略
10.4
11.(1)略 (2)△ABE是等腰直角三角形。理由略
12.(1)略 (2)(1)中的结论仍成立。理由略
13.(1) (2)1或
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
