第2章 特殊三角形 单元测试卷 (含部分答案)2025-2026学年浙教版数学八年级上册
文档属性
| 名称 | 第2章 特殊三角形 单元测试卷 (含部分答案)2025-2026学年浙教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 267.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 22:43:00 | ||
图片预览


文档简介
第2章特殊三角形 单元测试卷
(满分:120分 时间:120分钟)
一、选择题(本题有10 小题,每小题3分,共30分)
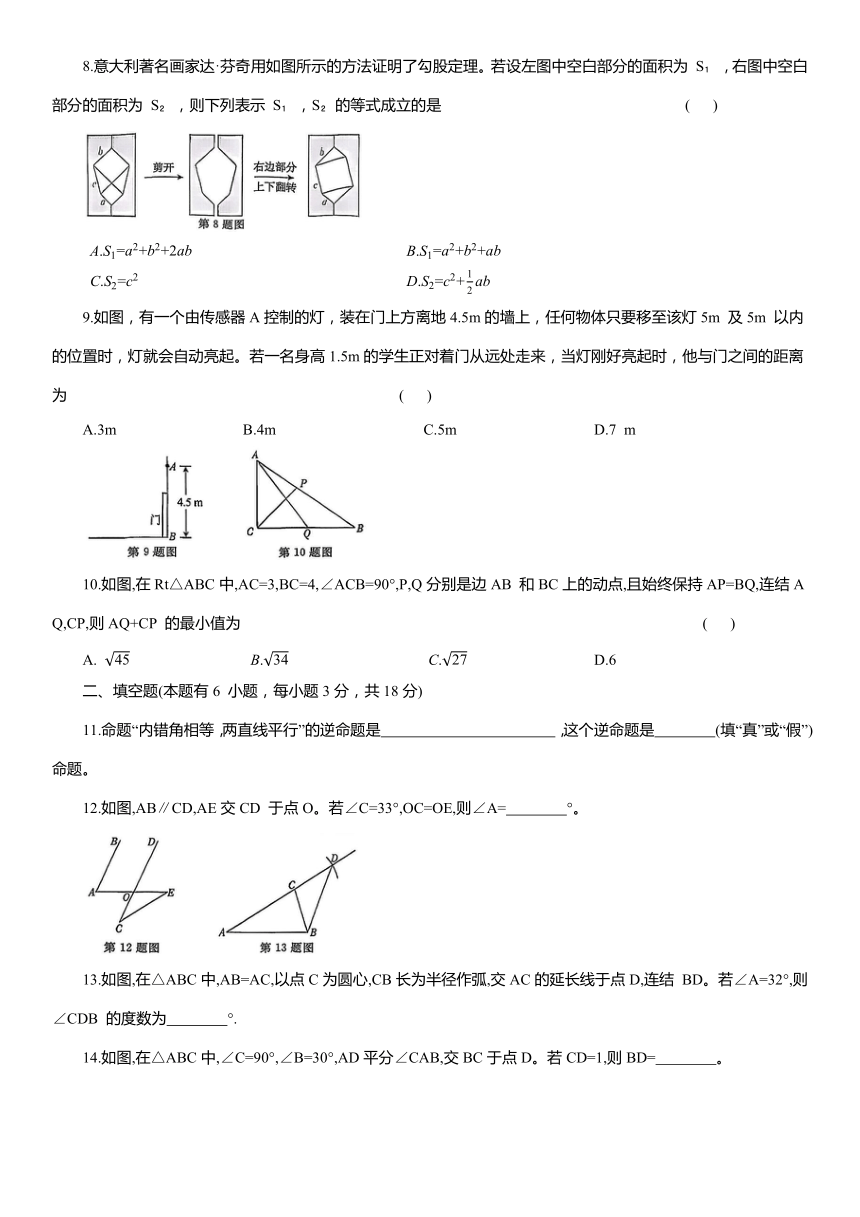
1.下列四个图形中,属于轴对称图形的是 ( )
2.如图,点 E在正方形ABCD 的边AB 上。若EB=1,EC=2,则正方形 ABCD 的面积为 ( )
A. B.3 C. D.5
3.如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线分别交AB,BC于点D,E,连结AE,则∠BAE 的度数为 ( )
A.80° B.60° C.50° D.40°
4.在△ABC中,∠ACB为钝角。用直尺和圆规在边AB上确定一点D,使∠ADC=2∠B,下列作图中,符合要求的是 ( )
5.如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,适当长为半径画弧,分别交AB,AC于点M 和点N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧相交于点 P,连结AP 并延长,交BC于点D。若△ACD 的面积为 8,则△ABD 的面积是 ( )
A.8 B.16 C.12 D.24
6.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E是AB 的中点,CD=DE=a,则AB的长为 ( )
A.2a C.3a
7.如图,在 Rt△ABC中, 点D 在AB 的延长线上,且CD=AB,则 BD 的长是 ( )
8.意大利著名画家达·芬奇用如图所示的方法证明了勾股定理。若设左图中空白部分的面积为 S ,右图中空白部分的面积为 S ,则下列表示 S ,S 的等式成立的是 ( )
9.如图,有一个由传感器A控制的灯,装在门上方离地4.5m的墙上,任何物体只要移至该灯5m 及5m 以内的位置时,灯就会自动亮起。若一名身高1.5m的学生正对着门从远处走来,当灯刚好亮起时,他与门之间的距离为 ( )
A.3m B.4m C.5m D.7 m
10.如图,在Rt△ABC中,AC=3,BC=4,∠ACB=90°,P,Q分别是边AB 和BC上的动点,且始终保持AP=BQ,连结AQ,CP,则AQ+CP 的最小值为 ( )
A. D.6
二、填空题(本题有6 小题,每小题3分,共18分)
11.命题“内错角相等,两直线平行”的逆命题是 ,这个逆命题是 (填“真”或“假”)命题。
12.如图,AB∥CD,AE交CD 于点O。若∠C=33°,OC=OE,则∠A= °。
13.如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径作弧,交AC的延长线于点D,连结 BD。若∠A=32°,则∠CDB 的度数为 °.
14.如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D。若CD=1,则BD= 。
15.如图,在△ABC中,∠ACB=90°,点D,E在AB上。若 BD=BC,AE=AC,则∠DCE的度数为 °。
16.如图,在△ACD中,AC=DC=2,∠ACD=90°。分别以△ACD的边AD,AC,CD 为直径画半圆,所得两个月形图案(图中阴影部分)的面积之和为 。
三、解答题(本题有 8 小题,共72 分)
17.(8分)如图,在△ABC中,D 是三角形内一点,连结DA,DB,DC。若∠1=∠2,∠3=∠4,求证:AB=AC。
18.(8分)如图,在等边三角形 ABC 中,点 D 在边 BC 上,点 E 在△ABC 外,AD=AE。若∠BAD=20°,∠DAE=70°,求∠CAE 和∠CDE 的度数。
19.(8分)如图,在 Rt△ABC中, 分别以点A,B为圆心,大于 的长为半径画弧,两弧相交于点 M,N,作直线MN,分别交AB,BC于点D,E,连结CD,AE。求:
(1)CD的长。
(2)△ACE 的周长。
20.(8分)根据下列素材,探索完成任务。
项目背景 我校八年级兴趣小组对“勾股树”展开了研究。
素材一 毕达哥拉斯树,也称“勾股树”,是由毕达哥拉斯根据勾股定理画出来的一个可以无限重复的树形图形(如图1),因为重复数次后的形状好似一棵树,所以被称为毕达哥拉斯树。
素材二 经过小组讨论,同学们对三角形作出相应的限制: 所画的基础三角形周长均为7 cm,其中一条边长固定为2cm 。
素材三 根据规则,三位同学分别画出了不同类型的树形图并进行探究(如图2)。
问题解决
任务一 (1)小明画出了锐角三角形ABC(类型①),AB=AC,BC=2cm,则(
任务二 (2)小金画出了直角三角形 DEF(类型②), ,计算 S 的值,并写出过程。
任务三 (3)小山画出了钝角三角形GHI(类型③),∠GIH=120°,HI=2cm,则
21.(8分)如图,AB=CD,AC与BD 相交于点G,过点D,B分别作DE⊥AC,BF⊥AC,垂足分别为E,F。
(1)如图1,点 E在点 F 的左侧,若AE=CF,求证:G是EF 的中点。
(2)如图2,点E在点F 的右侧,若AE=CF,则(1)中结论是否仍成立 请说明理由。
22.(10分)在 中,AB=AC,P 是BC 上任意一点。
(1)如图1,若点 P 在线段BC上,PF⊥AB 于点 F,PE⊥AC于点E,BD 为△ABC的高线,试探究 PE,PF与BD 之间的数量关系。
(2)如图2,若点 P在BC 的延长线上,PF⊥AB 于点F,PE⊥AC,交 AC 的延长线于点E,CD 是△ABC的高线,试探究 PE,PF 与CD 之间的数量关系。
23.(10分)如图,在△ACB中,∠ACB=90°,高线CD与角平分线AF 相交于点E,N为EF 的中点,过点 N 作AB 的平行线,交AC于点M,已知 BC=20,AB=25。
(1)求证:CE=CF。
(2)求 MN的长。
(3)连结 DN,求2DN 的值。
24.(12 分)【基础巩固】(1)如图1,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE。求证:△AEC≌△ADB。
【尝试应用】(2)如图2,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,B,D,E三点在同一条直线上,AC与BE 相交于点F,且 F 恰好为AC 的中点。
①求∠BEC 的度数。
②若CE=2,求△ACE的面积。
【拓展提高】(3)如图3,在△ABC与△ADE中,AB=AC,DA=DE,∠BAC=∠ADE=90°,BE 与CA 相交于点F,连结DF。若DC=DF,CD⊥DF,△BCF的面积为18,求 AF的长。
1. D 2. B 3. D 4. B 5. B 6. B 7. B 8. B 9. B 10. B
11.两直线平行,内错角相等 真 12.66 13.37 14.2
15.4516.2 17.略 18.∠CAE=30°。∠CDE=25°
19.(1) (2)3 20.(1)6.25 (3)
21.(1)略 (2)(1)中结论仍成立。理由略
22.(1)BD=PE+PF (2)CD=PF-PE
23.(1)略(2)
24.(1)略 (2)①90° ②2 (3)6
(满分:120分 时间:120分钟)
一、选择题(本题有10 小题,每小题3分,共30分)
1.下列四个图形中,属于轴对称图形的是 ( )
2.如图,点 E在正方形ABCD 的边AB 上。若EB=1,EC=2,则正方形 ABCD 的面积为 ( )
A. B.3 C. D.5
3.如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线分别交AB,BC于点D,E,连结AE,则∠BAE 的度数为 ( )
A.80° B.60° C.50° D.40°
4.在△ABC中,∠ACB为钝角。用直尺和圆规在边AB上确定一点D,使∠ADC=2∠B,下列作图中,符合要求的是 ( )
5.如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,适当长为半径画弧,分别交AB,AC于点M 和点N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧相交于点 P,连结AP 并延长,交BC于点D。若△ACD 的面积为 8,则△ABD 的面积是 ( )
A.8 B.16 C.12 D.24
6.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E是AB 的中点,CD=DE=a,则AB的长为 ( )
A.2a C.3a
7.如图,在 Rt△ABC中, 点D 在AB 的延长线上,且CD=AB,则 BD 的长是 ( )
8.意大利著名画家达·芬奇用如图所示的方法证明了勾股定理。若设左图中空白部分的面积为 S ,右图中空白部分的面积为 S ,则下列表示 S ,S 的等式成立的是 ( )
9.如图,有一个由传感器A控制的灯,装在门上方离地4.5m的墙上,任何物体只要移至该灯5m 及5m 以内的位置时,灯就会自动亮起。若一名身高1.5m的学生正对着门从远处走来,当灯刚好亮起时,他与门之间的距离为 ( )
A.3m B.4m C.5m D.7 m
10.如图,在Rt△ABC中,AC=3,BC=4,∠ACB=90°,P,Q分别是边AB 和BC上的动点,且始终保持AP=BQ,连结AQ,CP,则AQ+CP 的最小值为 ( )
A. D.6
二、填空题(本题有6 小题,每小题3分,共18分)
11.命题“内错角相等,两直线平行”的逆命题是 ,这个逆命题是 (填“真”或“假”)命题。
12.如图,AB∥CD,AE交CD 于点O。若∠C=33°,OC=OE,则∠A= °。
13.如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径作弧,交AC的延长线于点D,连结 BD。若∠A=32°,则∠CDB 的度数为 °.
14.如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D。若CD=1,则BD= 。
15.如图,在△ABC中,∠ACB=90°,点D,E在AB上。若 BD=BC,AE=AC,则∠DCE的度数为 °。
16.如图,在△ACD中,AC=DC=2,∠ACD=90°。分别以△ACD的边AD,AC,CD 为直径画半圆,所得两个月形图案(图中阴影部分)的面积之和为 。
三、解答题(本题有 8 小题,共72 分)
17.(8分)如图,在△ABC中,D 是三角形内一点,连结DA,DB,DC。若∠1=∠2,∠3=∠4,求证:AB=AC。
18.(8分)如图,在等边三角形 ABC 中,点 D 在边 BC 上,点 E 在△ABC 外,AD=AE。若∠BAD=20°,∠DAE=70°,求∠CAE 和∠CDE 的度数。
19.(8分)如图,在 Rt△ABC中, 分别以点A,B为圆心,大于 的长为半径画弧,两弧相交于点 M,N,作直线MN,分别交AB,BC于点D,E,连结CD,AE。求:
(1)CD的长。
(2)△ACE 的周长。
20.(8分)根据下列素材,探索完成任务。
项目背景 我校八年级兴趣小组对“勾股树”展开了研究。
素材一 毕达哥拉斯树,也称“勾股树”,是由毕达哥拉斯根据勾股定理画出来的一个可以无限重复的树形图形(如图1),因为重复数次后的形状好似一棵树,所以被称为毕达哥拉斯树。
素材二 经过小组讨论,同学们对三角形作出相应的限制: 所画的基础三角形周长均为7 cm,其中一条边长固定为2cm 。
素材三 根据规则,三位同学分别画出了不同类型的树形图并进行探究(如图2)。
问题解决
任务一 (1)小明画出了锐角三角形ABC(类型①),AB=AC,BC=2cm,则(
任务二 (2)小金画出了直角三角形 DEF(类型②), ,计算 S 的值,并写出过程。
任务三 (3)小山画出了钝角三角形GHI(类型③),∠GIH=120°,HI=2cm,则
21.(8分)如图,AB=CD,AC与BD 相交于点G,过点D,B分别作DE⊥AC,BF⊥AC,垂足分别为E,F。
(1)如图1,点 E在点 F 的左侧,若AE=CF,求证:G是EF 的中点。
(2)如图2,点E在点F 的右侧,若AE=CF,则(1)中结论是否仍成立 请说明理由。
22.(10分)在 中,AB=AC,P 是BC 上任意一点。
(1)如图1,若点 P 在线段BC上,PF⊥AB 于点 F,PE⊥AC于点E,BD 为△ABC的高线,试探究 PE,PF与BD 之间的数量关系。
(2)如图2,若点 P在BC 的延长线上,PF⊥AB 于点F,PE⊥AC,交 AC 的延长线于点E,CD 是△ABC的高线,试探究 PE,PF 与CD 之间的数量关系。
23.(10分)如图,在△ACB中,∠ACB=90°,高线CD与角平分线AF 相交于点E,N为EF 的中点,过点 N 作AB 的平行线,交AC于点M,已知 BC=20,AB=25。
(1)求证:CE=CF。
(2)求 MN的长。
(3)连结 DN,求2DN 的值。
24.(12 分)【基础巩固】(1)如图1,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE。求证:△AEC≌△ADB。
【尝试应用】(2)如图2,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,B,D,E三点在同一条直线上,AC与BE 相交于点F,且 F 恰好为AC 的中点。
①求∠BEC 的度数。
②若CE=2,求△ACE的面积。
【拓展提高】(3)如图3,在△ABC与△ADE中,AB=AC,DA=DE,∠BAC=∠ADE=90°,BE 与CA 相交于点F,连结DF。若DC=DF,CD⊥DF,△BCF的面积为18,求 AF的长。
1. D 2. B 3. D 4. B 5. B 6. B 7. B 8. B 9. B 10. B
11.两直线平行,内错角相等 真 12.66 13.37 14.2
15.4516.2 17.略 18.∠CAE=30°。∠CDE=25°
19.(1) (2)3 20.(1)6.25 (3)
21.(1)略 (2)(1)中结论仍成立。理由略
22.(1)BD=PE+PF (2)CD=PF-PE
23.(1)略(2)
24.(1)略 (2)①90° ②2 (3)6
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
