2.5~2.8阶段巩固练(四)(含部分答案)2025-2026学年浙教版数学八年级上册
文档属性
| 名称 | 2.5~2.8阶段巩固练(四)(含部分答案)2025-2026学年浙教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 139.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 09:25:45 | ||
图片预览

文档简介
2.5~2.8阶段巩固练(四)
一、选择题
1.下列各命题的逆命题,属于假命题的是 ( )
A.锐角三角形是等边三角形
B.如果两个三角形全等,那么这两个三角形的对应边相等
C.如果两个三角形全等,那么这两个三角形的对应角相等
D.直角三角形的两个锐角互余
2.能说明命题“若. ,则x≥3”为假命题的一个反例可以是 ( )
A. x=4 B. x=2
C. x=-4 D. x=-2
3.图1是第七届国际数学教育大会(ICME)的会徽,主体图案是由如图 2 的一连串直角三角形演化而成,其中 若 则a的值为 ( )
A. B. C.2 D.1
4.如图,△ABC的三边长为5,12,13,分别以三边为直径向上作半圆,则阴影部分图形的面积为()
A. 1 B.30 C.6013 D.60
5.如图,梯子AB长为2m ,顶端A 靠在墙上,这时梯子下端 B 与墙角C 的距离为1.2m,梯子滑动后停在 DE 的位置上,测得 BD长为0.4m ,则梯子顶端A下落了 ( )
A.0.4m B.0.5m C.0.6m D.0.7 m
6.有下列条件:①∠A+∠B=∠C;②∠A:∠B :∠C=1: 5:6;③∠A=90°-∠B;④∠A=∠B=∠C。其中能确定△ABC是直角三角形的有( )
A.①②③ B.①②④
C.③④ D.②③
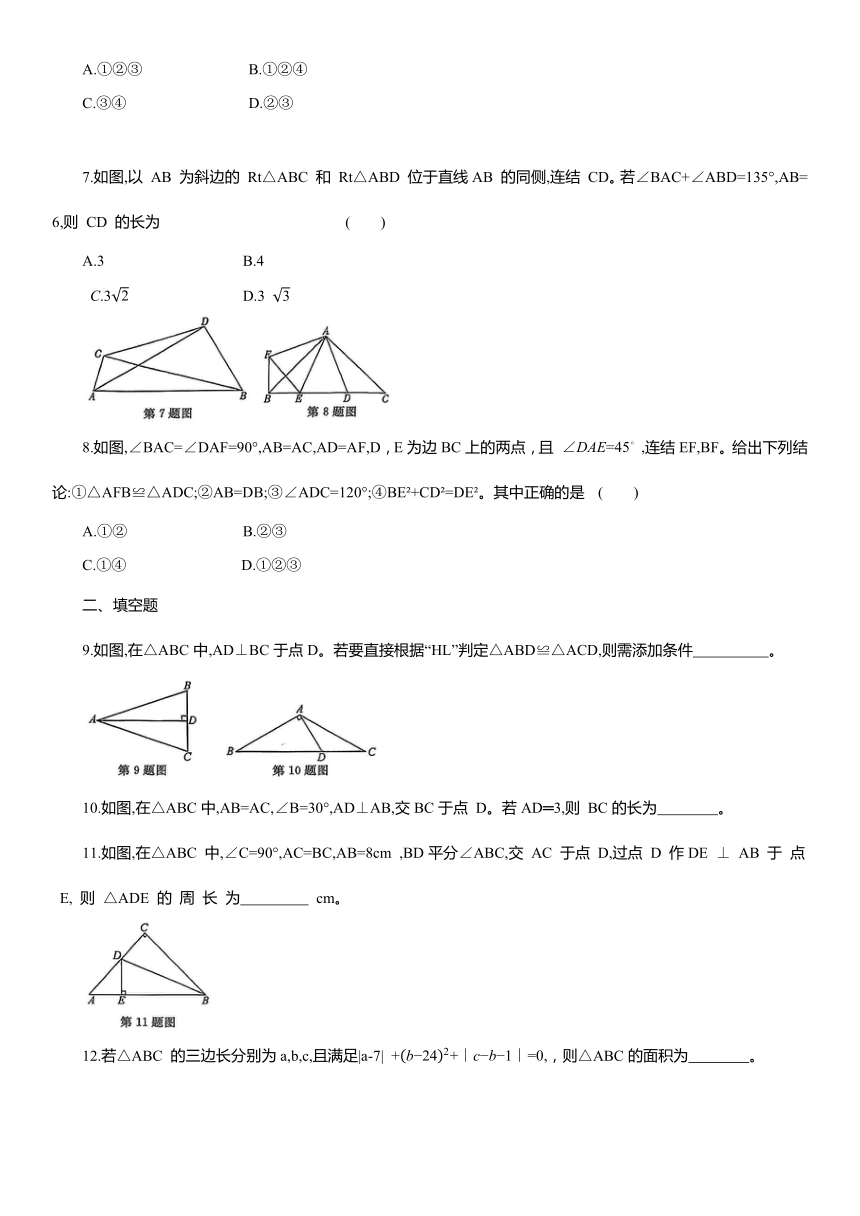
7.如图,以 AB 为斜边的 Rt△ABC 和 Rt△ABD 位于直线AB 的同侧,连结 CD。若∠BAC+∠ABD=135°,AB=6,则 CD 的长为 ( )
A.3 B.4
D.3
8.如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,D,E为边BC上的两点,且 连结EF,BF。给出下列结论:①△AFB≌△ADC;②AB=DB;③∠ADC=120°;④BE +CD =DE 。其中正确的是 ( )
A.①② B.②③
C.①④ D.①②③
二、填空题
9.如图,在△ABC中,AD⊥BC于点D。若要直接根据“HL”判定△ABD≌△ACD,则需添加条件 。
10.如图,在△ABC中,AB=AC,∠B=30°,AD⊥AB,交BC于点 D。若AD═3,则 BC的长为 。
11.如图,在△ABC 中,∠C=90°,AC=BC,AB=8cm ,BD平分∠ABC,交 AC 于点 D,过点 D 作DE ⊥ AB 于 点 E, 则 △ADE 的 周 长 为 cm。
12.若△ABC 的三边长分别为a,b,c,且满足|a-7| ,则△ABC的面积为 。
13.如图,已知 9∠ACD=45°,则 BD= 。
14.如图,CA⊥BC,AC=2 cm,BC=6 cm,射线 BM⊥BQ,动点 P 从点C 出发,以1 cm/s 的速度沿射线 CQ运动,N 为射线BM 上一动点,随着点 P 的运动而运动,且满足 PN=AB。当点 P 的运动时间为 秒时,△BCA 与以 P,N,B 为顶点的三角形全等。
三、解答题
15.如图,在△ABC和△DCB 中,∠A=∠D=90°,AC=BD,AC与BD 相交于点O。
(1)求证:△ABC≌△DCB。
(2)判断△OBC的形状,并说明理由。
16.如图,在四边形ABCD中,AB=BC=DA=1,CD 且AB⊥BC,求∠BAD 的度数。
17.如图1,在△ABC中,∠C=90°,AC=8,BC=6,D是AB 的中点,点 E 在线段AC 上,连结DE,过点D作DF⊥DE交直线BC 于点 F,连结 EF。
【初步尝试】
(1)如图 2,当 AE = 4 时,线段 EF 的长度是 ,线段 BF 的长度是 。
【结论探究】
(2)小宁猜想‘ 但她未能想出证明思路,小静介绍了添加辅助线的方法,如下表所示,请帮小宁完成证明。
如图 3,延长 ED 至点G,使 DG=DE,连结 BG,FG。
【拓展应用】
(3)如图4,当点 E 在线段CA 的延长线上时,连结DE,作DF⊥DE交直线BC 于点F,连结EF。请补全图形,并求出当AE=2时,线段 BF 的长。
阶段巩固练(四)
1. C 2. C 3. A 4. B 5. A 6. A 7. C 8. C
9. AB=AC10.9 11.8 12.84 13.
14.0或4或8或12
15.(1)略 (2)△OBC是等腰三角形。理由略
16.135°17.(1)53 (2)略 (3)补全图形略,BF=11
一、选择题
1.下列各命题的逆命题,属于假命题的是 ( )
A.锐角三角形是等边三角形
B.如果两个三角形全等,那么这两个三角形的对应边相等
C.如果两个三角形全等,那么这两个三角形的对应角相等
D.直角三角形的两个锐角互余
2.能说明命题“若. ,则x≥3”为假命题的一个反例可以是 ( )
A. x=4 B. x=2
C. x=-4 D. x=-2
3.图1是第七届国际数学教育大会(ICME)的会徽,主体图案是由如图 2 的一连串直角三角形演化而成,其中 若 则a的值为 ( )
A. B. C.2 D.1
4.如图,△ABC的三边长为5,12,13,分别以三边为直径向上作半圆,则阴影部分图形的面积为()
A. 1 B.30 C.6013 D.60
5.如图,梯子AB长为2m ,顶端A 靠在墙上,这时梯子下端 B 与墙角C 的距离为1.2m,梯子滑动后停在 DE 的位置上,测得 BD长为0.4m ,则梯子顶端A下落了 ( )
A.0.4m B.0.5m C.0.6m D.0.7 m
6.有下列条件:①∠A+∠B=∠C;②∠A:∠B :∠C=1: 5:6;③∠A=90°-∠B;④∠A=∠B=∠C。其中能确定△ABC是直角三角形的有( )
A.①②③ B.①②④
C.③④ D.②③
7.如图,以 AB 为斜边的 Rt△ABC 和 Rt△ABD 位于直线AB 的同侧,连结 CD。若∠BAC+∠ABD=135°,AB=6,则 CD 的长为 ( )
A.3 B.4
D.3
8.如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,D,E为边BC上的两点,且 连结EF,BF。给出下列结论:①△AFB≌△ADC;②AB=DB;③∠ADC=120°;④BE +CD =DE 。其中正确的是 ( )
A.①② B.②③
C.①④ D.①②③
二、填空题
9.如图,在△ABC中,AD⊥BC于点D。若要直接根据“HL”判定△ABD≌△ACD,则需添加条件 。
10.如图,在△ABC中,AB=AC,∠B=30°,AD⊥AB,交BC于点 D。若AD═3,则 BC的长为 。
11.如图,在△ABC 中,∠C=90°,AC=BC,AB=8cm ,BD平分∠ABC,交 AC 于点 D,过点 D 作DE ⊥ AB 于 点 E, 则 △ADE 的 周 长 为 cm。
12.若△ABC 的三边长分别为a,b,c,且满足|a-7| ,则△ABC的面积为 。
13.如图,已知 9∠ACD=45°,则 BD= 。
14.如图,CA⊥BC,AC=2 cm,BC=6 cm,射线 BM⊥BQ,动点 P 从点C 出发,以1 cm/s 的速度沿射线 CQ运动,N 为射线BM 上一动点,随着点 P 的运动而运动,且满足 PN=AB。当点 P 的运动时间为 秒时,△BCA 与以 P,N,B 为顶点的三角形全等。
三、解答题
15.如图,在△ABC和△DCB 中,∠A=∠D=90°,AC=BD,AC与BD 相交于点O。
(1)求证:△ABC≌△DCB。
(2)判断△OBC的形状,并说明理由。
16.如图,在四边形ABCD中,AB=BC=DA=1,CD 且AB⊥BC,求∠BAD 的度数。
17.如图1,在△ABC中,∠C=90°,AC=8,BC=6,D是AB 的中点,点 E 在线段AC 上,连结DE,过点D作DF⊥DE交直线BC 于点 F,连结 EF。
【初步尝试】
(1)如图 2,当 AE = 4 时,线段 EF 的长度是 ,线段 BF 的长度是 。
【结论探究】
(2)小宁猜想‘ 但她未能想出证明思路,小静介绍了添加辅助线的方法,如下表所示,请帮小宁完成证明。
如图 3,延长 ED 至点G,使 DG=DE,连结 BG,FG。
【拓展应用】
(3)如图4,当点 E 在线段CA 的延长线上时,连结DE,作DF⊥DE交直线BC 于点F,连结EF。请补全图形,并求出当AE=2时,线段 BF 的长。
阶段巩固练(四)
1. C 2. C 3. A 4. B 5. A 6. A 7. C 8. C
9. AB=AC10.9 11.8 12.84 13.
14.0或4或8或12
15.(1)略 (2)△OBC是等腰三角形。理由略
16.135°17.(1)53 (2)略 (3)补全图形略,BF=11
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
