专题5一次函数 专题讲练(含答案) 2025-2026学年浙教版数学八年级上册
文档属性
| 名称 | 专题5一次函数 专题讲练(含答案) 2025-2026学年浙教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 182.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 22:48:53 | ||
图片预览


文档简介
专题5 一次函数
题型归类
题型一 函数的概念及函数图象
【典例1】向如图所示的空容器内匀速注水,从水刚接触底部时开始计时,直至把容器注满。在注水过程中,设容器内底部所受水的压强为y帕,时间为x秒,则y关于x的函数图象大致为( )
【点悟】解这类用函数图象描述事物的变化规律的问题时,关键是正确分析事物的变化过程,理解函数图象的横、纵坐标的含义,同时要注意函数自变量的取值范围。
【变式1】如图所示的图象对应的函数表达式为( )
D. y=1-|x-1|(0≤x≤2)
题型二 一次函数的图象与性质
【典例2】当b<0时,一次函数y=x+b的图象可能是 ( )
【点悟】一次函数y= kx+b(k≠0)的图象与性质和表达式中k,b的关系如下表所示:
k>0 k<0
图象
b>0 b=0 b<0 b>0 b=0 b<0
经过象限 一、二、三 一、三 一、三、四 一、二、四 二、四 二、三、四
增减性 y随x的增大而增大 y随x的增大而减小
【变式2-1】已知一次函数 和 nx+m(mn≠0),则两函数在同一平面直角坐标系中的图象可能是 ( )
【变式2-2】直线 y=-2x-1 向上平移3个单位得到的直线的函数表达式为 。题型三 求一次函数的表达式
【典例3】已知一次函数y= mx+m-1(m≠0)过点(1,3)。
(1)求这个一次函数的表达式。
(2)当-2≤x<1时,求y的取值范围。
【点悟】求一次函数的表达式通常是把已知点的坐标代入表达式,运用待定系数法求出k,b的值。当求与坐标轴的交点坐标时,只要根据坐标轴的坐标特征代入表达式算出符合题意的解即可。
【变式3】已知 y关于x的一次函数y=mx+2-2m(m≠0且m≠1),其图象交x轴于点A,交y轴于点B,O为坐标原点。
(1)若OB=6,求此时m的值。
(2)该函数图象必过一定点,请求出该定点的坐标。
题型四 一次函数与方程(组)、不等式(组)的关系
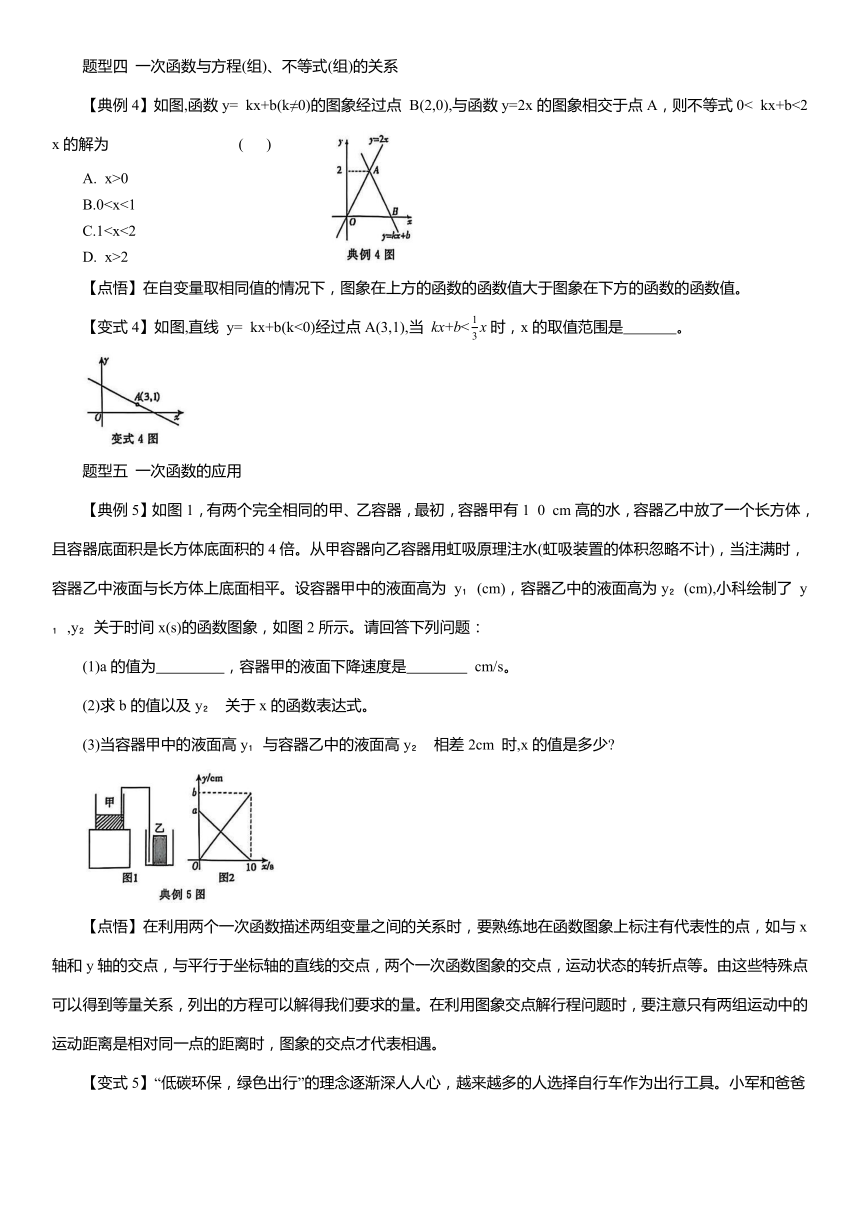
【典例4】如图,函数y= kx+b(k≠0)的图象经过点 B(2,0),与函数y=2x的图象相交于点A,则不等式0< kx+b<2x的解为 ( )
A. x>0
B.0C.1D. x>2
【点悟】在自变量取相同值的情况下,图象在上方的函数的函数值大于图象在下方的函数的函数值。
【变式4】如图,直线 y= kx+b(k<0)经过点A(3,1),当 时,x的取值范围是 。
题型五 一次函数的应用
【典例5】如图1,有两个完全相同的甲、乙容器,最初,容器甲有1 0 cm高的水,容器乙中放了一个长方体,且容器底面积是长方体底面积的4倍。从甲容器向乙容器用虹吸原理注水(虹吸装置的体积忽略不计),当注满时,容器乙中液面与长方体上底面相平。设容器甲中的液面高为 y (cm),容器乙中的液面高为y (cm),小科绘制了 y ,y 关于时间x(s)的函数图象,如图2所示。请回答下列问题:
(1)a的值为 ,容器甲的液面下降速度是 cm/s。
(2)求b的值以及y 关于x的函数表达式。
(3)当容器甲中的液面高y 与容器乙中的液面高y 相差2cm 时,x的值是多少
【点悟】在利用两个一次函数描述两组变量之间的关系时,要熟练地在函数图象上标注有代表性的点,如与x轴和y轴的交点,与平行于坐标轴的直线的交点,两个一次函数图象的交点,运动状态的转折点等。由这些特殊点可以得到等量关系,列出的方程可以解得我们要求的量。在利用图象交点解行程问题时,要注意只有两组运动中的运动距离是相对同一点的距离时,图象的交点才代表相遇。
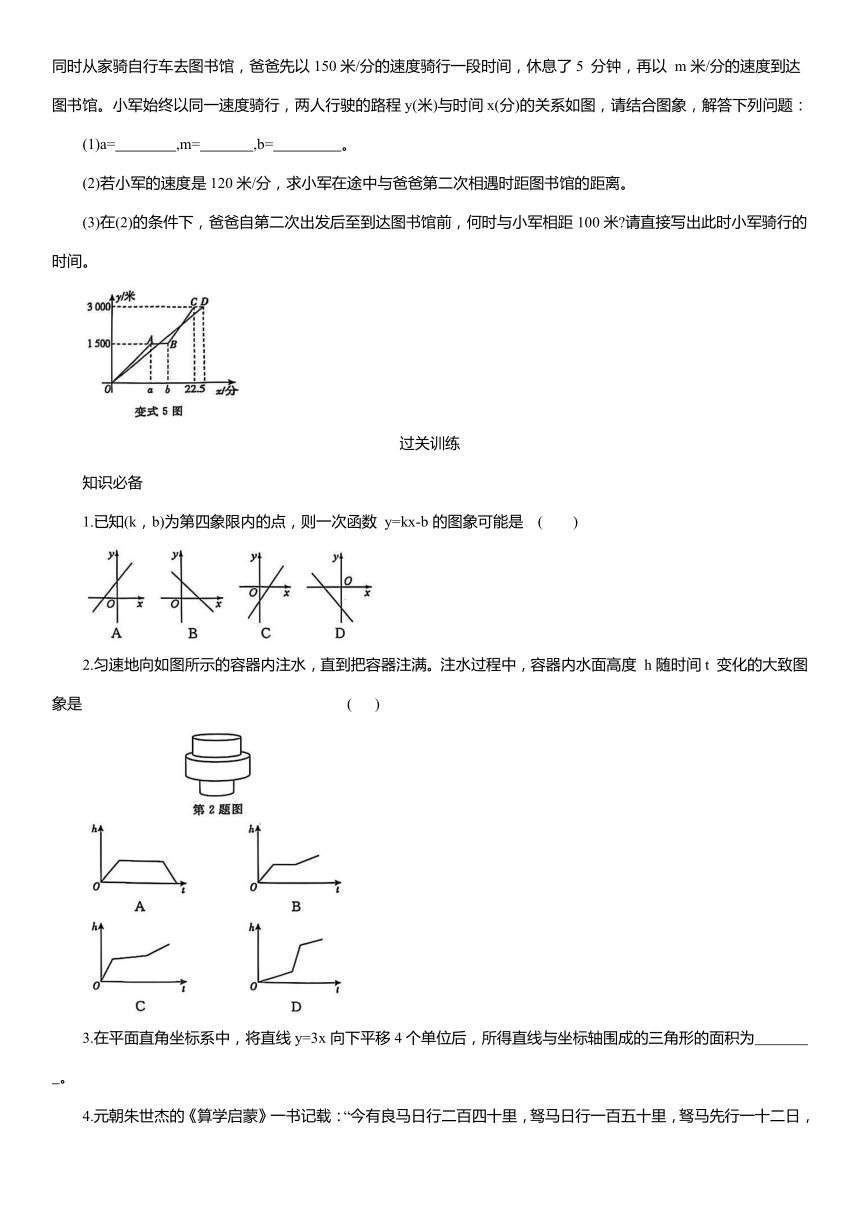
【变式5】“低碳环保,绿色出行”的理念逐渐深人人心,越来越多的人选择自行车作为出行工具。小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5 分钟,再以 m米/分的速度到达图书馆。小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分)的关系如图,请结合图象,解答下列问题:
(1)a= ,m= ,b= 。
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时距图书馆的距离。
(3)在(2)的条件下,爸爸自第二次出发后至到达图书馆前,何时与小军相距100米 请直接写出此时小军骑行的时间。
过关训练
知识必备
1.已知(k,b)为第四象限内的点,则一次函数 y=kx-b的图象可能是 ( )
2.匀速地向如图所示的容器内注水,直到把容器注满。注水过程中,容器内水面高度 h随时间t 变化的大致图象是 ( )
3.在平面直角坐标系中,将直线y=3x向下平移4个单位后,所得直线与坐标轴围成的三角形的面积为 。
4.元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之。”方方想到了用一次函数来解决这个问题,他画出两匹马行走的路程s(里)关于驽马行走的时间. t(日)的函数图象(如图),并说只要求出两图象的交点 P 的坐标就可以了。方方的说法对吗 请你算出点 P 的坐标并写出良马出发后几日追上驽马。
5.如图,直线 y= kx+b(k≠0)过点A(0,5),B(5,0)。
(1)求直线 AB的表达式。
(2)若直线 y=2x-4与直线 AB 相交于点C,求点C的坐标。
(3)根据图象直接写出关于x的不等式2x-4≥kx+b的解。
6.某游泳馆推出了两种收费方式。
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人使用一年,凭卡游泳,每次游泳再付费30元;
方式二:顾客不购买会员卡,每次游泳付费40元。设小亮在一年内来此游泳馆的次数是x,选择方式一的总费用为 y (元),选择方式二的总费用为y (元)。
(1)请分别写出y ,y 与x之间的函数表达式。
(2)小亮一年内在此游泳馆游泳的次数x在什么范围时,选择方式一比方式二省钱
7.甲、乙两位同学周末相约去游玩,沿同一路线从A地出发前往B 地,甲、乙分别以不同的速度匀速前行,乙比甲晚0.5h出发,并且在中途停留1 h后,按原来速度的一半继续前进。在此过程中,甲、乙两人离A地的路程s(km)与甲出发的时间t(h)之间的关系如图所示。有下列说法:①A,B两地相距24 km;②甲比乙晚到B 地1 h;③乙从A 地刚出发时的速度为72km/h;④乙出发 h时与甲第三次相遇。其中正确的是 ( )
A.①② B.③④
C.①②③ D.①②③④
8.印数x的关系如下表:
印数x/千册 1≤x<5 x≥5
彩色/(元/张) 2.2 2.0
黑白/(元/张) 0.7 0.6
(1)印制这批纪念册需制版费多少元
(2)求出 y关于x 的函数表达式。
(3)如果该校希望印数至少为4千册,总费用最多为61 820元,求印数的取值范围。
9.如图1,在平面直角坐标系中,直线 y=x+6与x轴相交于点A,与y轴相交于点B,P为线段BO 上的动点,连结AP,作点 O 关于线段AP 的对称点D,连结AD,DP。
(1)求A,B两点的坐标。
(2)如图2,当点 D落在直线 AB上时,求点 P 的坐标。
(3)如图3,作点A关于y轴的对称点 C,连结 BC,E为BC的中点,连结DE,求线段DE长的最小值。
专题5 一次函数
题型归类
【典例1】B
【变式1】B
【典例2】B
【变式2-1】A
【变式2-2】y=-2x+2
【典例3】(1)y=2x+1 (2)-3≤y<3
【变式3】(1)-2或4 (2)(2,2)
【典例4】C
【变式4】x>3
【典例5】(1)101 (
(3) 或
【变式5】(1)10 15 200 (2)750米 (3)17.5或20分钟过关训练
1. A 2. C 3.
4.方方的说法对。点 P 的坐标为(32,4 800),良马出发后20日追上驽马
5.(1)y=-x+5(2)(3,2) (3)x≥3
6.(1)y =30x+200,y =40x (2)x>207. D
8.(1)1 500元
(3)4≤x≤4.64或5≤x≤5.2
9.(1)点 A(-6,0)。点 B(0,6) (2)点.
题型归类
题型一 函数的概念及函数图象
【典例1】向如图所示的空容器内匀速注水,从水刚接触底部时开始计时,直至把容器注满。在注水过程中,设容器内底部所受水的压强为y帕,时间为x秒,则y关于x的函数图象大致为( )
【点悟】解这类用函数图象描述事物的变化规律的问题时,关键是正确分析事物的变化过程,理解函数图象的横、纵坐标的含义,同时要注意函数自变量的取值范围。
【变式1】如图所示的图象对应的函数表达式为( )
D. y=1-|x-1|(0≤x≤2)
题型二 一次函数的图象与性质
【典例2】当b<0时,一次函数y=x+b的图象可能是 ( )
【点悟】一次函数y= kx+b(k≠0)的图象与性质和表达式中k,b的关系如下表所示:
k>0 k<0
图象
b>0 b=0 b<0 b>0 b=0 b<0
经过象限 一、二、三 一、三 一、三、四 一、二、四 二、四 二、三、四
增减性 y随x的增大而增大 y随x的增大而减小
【变式2-1】已知一次函数 和 nx+m(mn≠0),则两函数在同一平面直角坐标系中的图象可能是 ( )
【变式2-2】直线 y=-2x-1 向上平移3个单位得到的直线的函数表达式为 。题型三 求一次函数的表达式
【典例3】已知一次函数y= mx+m-1(m≠0)过点(1,3)。
(1)求这个一次函数的表达式。
(2)当-2≤x<1时,求y的取值范围。
【点悟】求一次函数的表达式通常是把已知点的坐标代入表达式,运用待定系数法求出k,b的值。当求与坐标轴的交点坐标时,只要根据坐标轴的坐标特征代入表达式算出符合题意的解即可。
【变式3】已知 y关于x的一次函数y=mx+2-2m(m≠0且m≠1),其图象交x轴于点A,交y轴于点B,O为坐标原点。
(1)若OB=6,求此时m的值。
(2)该函数图象必过一定点,请求出该定点的坐标。
题型四 一次函数与方程(组)、不等式(组)的关系
【典例4】如图,函数y= kx+b(k≠0)的图象经过点 B(2,0),与函数y=2x的图象相交于点A,则不等式0< kx+b<2x的解为 ( )
A. x>0
B.0
【点悟】在自变量取相同值的情况下,图象在上方的函数的函数值大于图象在下方的函数的函数值。
【变式4】如图,直线 y= kx+b(k<0)经过点A(3,1),当 时,x的取值范围是 。
题型五 一次函数的应用
【典例5】如图1,有两个完全相同的甲、乙容器,最初,容器甲有1 0 cm高的水,容器乙中放了一个长方体,且容器底面积是长方体底面积的4倍。从甲容器向乙容器用虹吸原理注水(虹吸装置的体积忽略不计),当注满时,容器乙中液面与长方体上底面相平。设容器甲中的液面高为 y (cm),容器乙中的液面高为y (cm),小科绘制了 y ,y 关于时间x(s)的函数图象,如图2所示。请回答下列问题:
(1)a的值为 ,容器甲的液面下降速度是 cm/s。
(2)求b的值以及y 关于x的函数表达式。
(3)当容器甲中的液面高y 与容器乙中的液面高y 相差2cm 时,x的值是多少
【点悟】在利用两个一次函数描述两组变量之间的关系时,要熟练地在函数图象上标注有代表性的点,如与x轴和y轴的交点,与平行于坐标轴的直线的交点,两个一次函数图象的交点,运动状态的转折点等。由这些特殊点可以得到等量关系,列出的方程可以解得我们要求的量。在利用图象交点解行程问题时,要注意只有两组运动中的运动距离是相对同一点的距离时,图象的交点才代表相遇。
【变式5】“低碳环保,绿色出行”的理念逐渐深人人心,越来越多的人选择自行车作为出行工具。小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5 分钟,再以 m米/分的速度到达图书馆。小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分)的关系如图,请结合图象,解答下列问题:
(1)a= ,m= ,b= 。
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时距图书馆的距离。
(3)在(2)的条件下,爸爸自第二次出发后至到达图书馆前,何时与小军相距100米 请直接写出此时小军骑行的时间。
过关训练
知识必备
1.已知(k,b)为第四象限内的点,则一次函数 y=kx-b的图象可能是 ( )
2.匀速地向如图所示的容器内注水,直到把容器注满。注水过程中,容器内水面高度 h随时间t 变化的大致图象是 ( )
3.在平面直角坐标系中,将直线y=3x向下平移4个单位后,所得直线与坐标轴围成的三角形的面积为 。
4.元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之。”方方想到了用一次函数来解决这个问题,他画出两匹马行走的路程s(里)关于驽马行走的时间. t(日)的函数图象(如图),并说只要求出两图象的交点 P 的坐标就可以了。方方的说法对吗 请你算出点 P 的坐标并写出良马出发后几日追上驽马。
5.如图,直线 y= kx+b(k≠0)过点A(0,5),B(5,0)。
(1)求直线 AB的表达式。
(2)若直线 y=2x-4与直线 AB 相交于点C,求点C的坐标。
(3)根据图象直接写出关于x的不等式2x-4≥kx+b的解。
6.某游泳馆推出了两种收费方式。
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人使用一年,凭卡游泳,每次游泳再付费30元;
方式二:顾客不购买会员卡,每次游泳付费40元。设小亮在一年内来此游泳馆的次数是x,选择方式一的总费用为 y (元),选择方式二的总费用为y (元)。
(1)请分别写出y ,y 与x之间的函数表达式。
(2)小亮一年内在此游泳馆游泳的次数x在什么范围时,选择方式一比方式二省钱
7.甲、乙两位同学周末相约去游玩,沿同一路线从A地出发前往B 地,甲、乙分别以不同的速度匀速前行,乙比甲晚0.5h出发,并且在中途停留1 h后,按原来速度的一半继续前进。在此过程中,甲、乙两人离A地的路程s(km)与甲出发的时间t(h)之间的关系如图所示。有下列说法:①A,B两地相距24 km;②甲比乙晚到B 地1 h;③乙从A 地刚出发时的速度为72km/h;④乙出发 h时与甲第三次相遇。其中正确的是 ( )
A.①② B.③④
C.①②③ D.①②③④
8.印数x的关系如下表:
印数x/千册 1≤x<5 x≥5
彩色/(元/张) 2.2 2.0
黑白/(元/张) 0.7 0.6
(1)印制这批纪念册需制版费多少元
(2)求出 y关于x 的函数表达式。
(3)如果该校希望印数至少为4千册,总费用最多为61 820元,求印数的取值范围。
9.如图1,在平面直角坐标系中,直线 y=x+6与x轴相交于点A,与y轴相交于点B,P为线段BO 上的动点,连结AP,作点 O 关于线段AP 的对称点D,连结AD,DP。
(1)求A,B两点的坐标。
(2)如图2,当点 D落在直线 AB上时,求点 P 的坐标。
(3)如图3,作点A关于y轴的对称点 C,连结 BC,E为BC的中点,连结DE,求线段DE长的最小值。
专题5 一次函数
题型归类
【典例1】B
【变式1】B
【典例2】B
【变式2-1】A
【变式2-2】y=-2x+2
【典例3】(1)y=2x+1 (2)-3≤y<3
【变式3】(1)-2或4 (2)(2,2)
【典例4】C
【变式4】x>3
【典例5】(1)101 (
(3) 或
【变式5】(1)10 15 200 (2)750米 (3)17.5或20分钟过关训练
1. A 2. C 3.
4.方方的说法对。点 P 的坐标为(32,4 800),良马出发后20日追上驽马
5.(1)y=-x+5(2)(3,2) (3)x≥3
6.(1)y =30x+200,y =40x (2)x>207. D
8.(1)1 500元
(3)4≤x≤4.64或5≤x≤5.2
9.(1)点 A(-6,0)。点 B(0,6) (2)点.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
