专题 2 特殊三角形专题讲练(含部分答案) 2025-2026学年浙教版数学八年级上册
文档属性
| 名称 | 专题 2 特殊三角形专题讲练(含部分答案) 2025-2026学年浙教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 209.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 09:39:48 | ||
图片预览



文档简介
专题 2 特殊三角形
题型归类
题型一 轴对称及轴对称图形
【典例1】下列表示天气的标志中,属于轴对称图形的是 ( )
【点悟】判断一个图形是否属于轴对称图形的主要依据是轴对称图形的定义,即将图形沿着某条直线折叠,看直线两旁的部分是否能够完全重合,能够完全重合的就是轴对称图形,否则就不是。
【变式1】将一张正方形纸片按如图所示的步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是 ( )
题型二 等腰三角形的性质与判定
【典例2】如图,在△ABC中,AB=AC,点 D 在AC边上(不与A,C重合),连结BD,BD=AB。
(1)设∠C=α,∠ABD=β。
①当α=50°时,求β。
②请求出β与α的数量关系。
(2)若AB=5,BC=6,求AD的长。
【点悟】在求等腰三角形中角的度数或边的长度时,要熟练掌握等腰三角形的底角相等与三线合一的性质。
【变式2】如图,在锐角三角形 ABC中,E是AB边上一点,BE=CE,AD⊥BC于点D,AD与EC 相交于点G。
(1)求证:EA=EG。
(2)若BE=10,CD=3,G为CE中点,求 AG的长。
题型三 等边三角形的性质与判定
【典例3】如图,已知△ABC和△BDE都是等边三角形,其中点 E 在 BC 边上,连结 AE,CD,求证:AE=CD。
【点悟】等边三角形不仅有“三条边都相等”和“三个内角都为 60°”的性质,还拥有等腰三角形的所有性质。
【变式3】在边长为2的等边三角形 ABC中,D为边BC上的任意一点,过点 D作DE⊥AB于点 E,DF⊥AC于点 F,则 DE+DF= 。
题型四 直角三角形与勾股定理
【典例4】如图,在Rt△ABC中,∠ACB=90°,D是AB 的中点,BE⊥CD,交CD的延长线于点E。若AC=3,BC=4,则 BE的长为 。
【点悟】勾股定理的作用是已知直角三角形的任意两边长,求第三边的长,我们要会灵活运用勾股定理的不同形式求解。在 Rt△ABC 中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,勾股定理的不同形式有:
【变式 4-1】如图,在四边形 ABCD 中,∠A=60°,∠B=∠D=90°,BC=3,CD=6,则 AB 的长为 。
【变式4-2】如图,每个小正方形的边长均为1,点A,B,C,D在小正方形的顶点上。
(1)求四边形ABCD 的周长。
(2)求证:∠BCD=90°。
题型五 直角三角形全等的判定
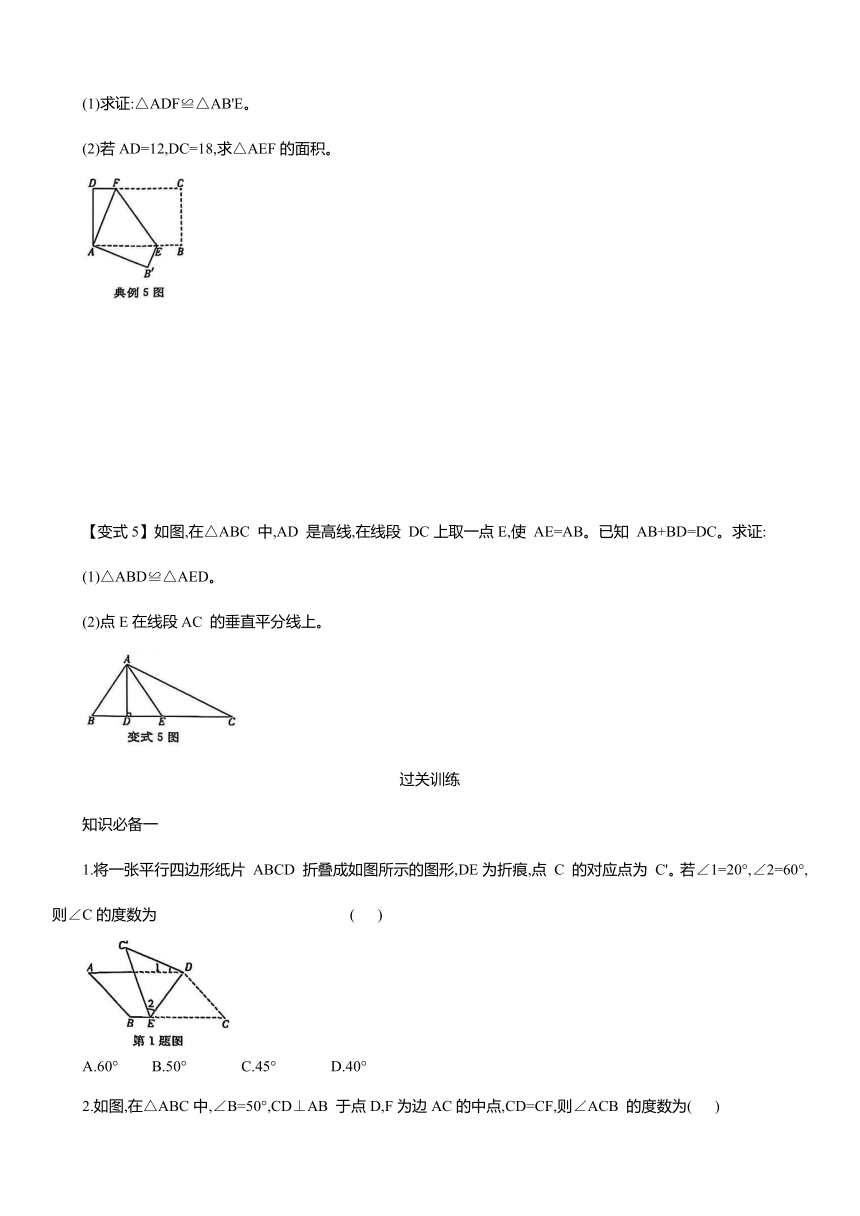
【典例5】如图,将长方形纸片ABCD 折叠,使点C与点A 重合,折痕分别与AB,DC相交于点E,F。
(1)求证:△ADF≌△AB'E。
(2)若AD=12,DC=18,求△AEF的面积。
【变式5】如图,在△ABC 中,AD 是高线,在线段 DC上取一点E,使 AE=AB。已知 AB+BD=DC。求证:
(1)△ABD≌△AED。
(2)点E在线段AC 的垂直平分线上。
过关训练
知识必备一
1.将一张平行四边形纸片 ABCD 折叠成如图所示的图形,DE为折痕,点 C 的对应点为 C'。若∠1=20°,∠2=60°,则∠C的度数为 ( )
A.60° B.50° C.45° D.40°
2.如图,在△ABC中,∠B=50°,CD⊥AB 于点D,F为边AC的中点,CD=CF,则∠ACB 的度数为( )
A.90° B.100°
C.110° D.120°
3.如图,在△ABE中,BA=BE,F为AE 的中点。若∠ABC= 34°,∠C = 50°, 则∠CAE 的度 数为 °。
4.为了比较 与 的大小,可以构造如图所示的图形进行推算,其中∠C=90°,BC=3,点 D 在边BC 上,且 BD=AC=1。通过计算可得, \sqrt{10} (填“>”“<”或“=”)。
5.如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为 D,E,F分别是线段 AD 和AB上的两个动点,连结CE,EF,则CE+EF 的最小值为 。
6.如图1,在3×3的网格中,△ABC三个顶点均在小方格的顶点上,这样的三角形叫作格点三角形。图1中画出了一个格点三角形(阴影部分),它与原△ABC关于某条直线成轴对称。请再在图2、图3、图4中,各画一个和原三角形成轴对称的格点三角形,并将所画的格点三角形涂上阴影(不能重复)。
7.如图,∠ACB=90°,AC=AD,过点 D作DE⊥AB,垂足为 D,交 BC于点E。求证:△CDE 是等腰三角形。
8.如图,在△ABC中,AD 是边 BC 上的高线,CE 是边AB上的中线,DG⊥CE于点G,CD=AE。
(1)求证:CG=EG。
(2)已知 BC=13,CD=5,求△CDG的面积。
能力突破一
9.如图1,四个全等的直角三角形围成一个大正方形,中间是一个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”。在此图形中,连结四条线段得到如图2 所示的图案,记阴影部分的面积为 S ,空白部分的面积为S ,大正方形的边长为m,小正方形的边长为n。若 则n/m的值为 。
10.如图,△ABC 是边长为 6 cm 的等边三角形,点P,Q分别从顶点A,B 同时出发,点 P 沿射线AB运动,点Q沿折线BC-CA 运动,且它们的速度都为1cm/s。当点Q到达点A 时,点 P 随之停止运动。连结 PQ,PC,设点 P 的运动时间为t(s)。
(1)当点 Q 在线段 BC 上运动时,BQ 的长为 cm,BP 的长为 cm(均用含 t的代数式表示)。
(2)当 PQ与△ABC的一条边垂直时,求t的值。
(3)在点 Q 从点 C 运动到点 A 的过程中,连结PQ,直接写出 PQ中点经过的路径长。
11.我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高线长的平方,则称这个三角形为“勾股高三角形”,两边交点为勾股顶点。
特例感知
(1)①等腰直角三角形 “勾股高三角形”(填“是”或者“不是”)。
②如图1,已知△ABC为“勾股高三角形”,其中C为勾股顶点,CD 是 AB 边上的高线。若 BD=2AD=2,试求线段CD的长度。
深入探究
(2)如图2,已知△ABC 为“勾股高三角形”,其中C为勾股顶点且CA>CB,CD 是 AB 边上的高线。试探究线段 AD 与CB 的数量关系,并给予证明。
推广应用
(3)如图3,等腰三角形ABC为“勾股高三角形”,其中AB=AC>BC,CD为AB 边上的高线,过点D作BC 边的平行线,与AC 边相交于点 E。若CE=a,试求线段 DE的长度。
题型归类
【典例1】A
【变式1】A
【典例2】(1)①20° ②β=4a-180° (2)
【变式2】(1)略 (2)8
【典例3】略
【变式3】
【典例4】
【变式
【变式 (2)略
【典例5】(1)略 (2)78
【变式5】略
过关训练
1. D 2. B 3.23 4.> 5. 7 6.略 7.略
8.(1)略(2)
10.(1)t 6-t (2)2或4或8 (3)3c m
11.(1)①是 ② (2)AD=CB。证明略 (3)2a
题型归类
题型一 轴对称及轴对称图形
【典例1】下列表示天气的标志中,属于轴对称图形的是 ( )
【点悟】判断一个图形是否属于轴对称图形的主要依据是轴对称图形的定义,即将图形沿着某条直线折叠,看直线两旁的部分是否能够完全重合,能够完全重合的就是轴对称图形,否则就不是。
【变式1】将一张正方形纸片按如图所示的步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是 ( )
题型二 等腰三角形的性质与判定
【典例2】如图,在△ABC中,AB=AC,点 D 在AC边上(不与A,C重合),连结BD,BD=AB。
(1)设∠C=α,∠ABD=β。
①当α=50°时,求β。
②请求出β与α的数量关系。
(2)若AB=5,BC=6,求AD的长。
【点悟】在求等腰三角形中角的度数或边的长度时,要熟练掌握等腰三角形的底角相等与三线合一的性质。
【变式2】如图,在锐角三角形 ABC中,E是AB边上一点,BE=CE,AD⊥BC于点D,AD与EC 相交于点G。
(1)求证:EA=EG。
(2)若BE=10,CD=3,G为CE中点,求 AG的长。
题型三 等边三角形的性质与判定
【典例3】如图,已知△ABC和△BDE都是等边三角形,其中点 E 在 BC 边上,连结 AE,CD,求证:AE=CD。
【点悟】等边三角形不仅有“三条边都相等”和“三个内角都为 60°”的性质,还拥有等腰三角形的所有性质。
【变式3】在边长为2的等边三角形 ABC中,D为边BC上的任意一点,过点 D作DE⊥AB于点 E,DF⊥AC于点 F,则 DE+DF= 。
题型四 直角三角形与勾股定理
【典例4】如图,在Rt△ABC中,∠ACB=90°,D是AB 的中点,BE⊥CD,交CD的延长线于点E。若AC=3,BC=4,则 BE的长为 。
【点悟】勾股定理的作用是已知直角三角形的任意两边长,求第三边的长,我们要会灵活运用勾股定理的不同形式求解。在 Rt△ABC 中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,勾股定理的不同形式有:
【变式 4-1】如图,在四边形 ABCD 中,∠A=60°,∠B=∠D=90°,BC=3,CD=6,则 AB 的长为 。
【变式4-2】如图,每个小正方形的边长均为1,点A,B,C,D在小正方形的顶点上。
(1)求四边形ABCD 的周长。
(2)求证:∠BCD=90°。
题型五 直角三角形全等的判定
【典例5】如图,将长方形纸片ABCD 折叠,使点C与点A 重合,折痕分别与AB,DC相交于点E,F。
(1)求证:△ADF≌△AB'E。
(2)若AD=12,DC=18,求△AEF的面积。
【变式5】如图,在△ABC 中,AD 是高线,在线段 DC上取一点E,使 AE=AB。已知 AB+BD=DC。求证:
(1)△ABD≌△AED。
(2)点E在线段AC 的垂直平分线上。
过关训练
知识必备一
1.将一张平行四边形纸片 ABCD 折叠成如图所示的图形,DE为折痕,点 C 的对应点为 C'。若∠1=20°,∠2=60°,则∠C的度数为 ( )
A.60° B.50° C.45° D.40°
2.如图,在△ABC中,∠B=50°,CD⊥AB 于点D,F为边AC的中点,CD=CF,则∠ACB 的度数为( )
A.90° B.100°
C.110° D.120°
3.如图,在△ABE中,BA=BE,F为AE 的中点。若∠ABC= 34°,∠C = 50°, 则∠CAE 的度 数为 °。
4.为了比较 与 的大小,可以构造如图所示的图形进行推算,其中∠C=90°,BC=3,点 D 在边BC 上,且 BD=AC=1。通过计算可得, \sqrt{10} (填“>”“<”或“=”)。
5.如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为 D,E,F分别是线段 AD 和AB上的两个动点,连结CE,EF,则CE+EF 的最小值为 。
6.如图1,在3×3的网格中,△ABC三个顶点均在小方格的顶点上,这样的三角形叫作格点三角形。图1中画出了一个格点三角形(阴影部分),它与原△ABC关于某条直线成轴对称。请再在图2、图3、图4中,各画一个和原三角形成轴对称的格点三角形,并将所画的格点三角形涂上阴影(不能重复)。
7.如图,∠ACB=90°,AC=AD,过点 D作DE⊥AB,垂足为 D,交 BC于点E。求证:△CDE 是等腰三角形。
8.如图,在△ABC中,AD 是边 BC 上的高线,CE 是边AB上的中线,DG⊥CE于点G,CD=AE。
(1)求证:CG=EG。
(2)已知 BC=13,CD=5,求△CDG的面积。
能力突破一
9.如图1,四个全等的直角三角形围成一个大正方形,中间是一个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”。在此图形中,连结四条线段得到如图2 所示的图案,记阴影部分的面积为 S ,空白部分的面积为S ,大正方形的边长为m,小正方形的边长为n。若 则n/m的值为 。
10.如图,△ABC 是边长为 6 cm 的等边三角形,点P,Q分别从顶点A,B 同时出发,点 P 沿射线AB运动,点Q沿折线BC-CA 运动,且它们的速度都为1cm/s。当点Q到达点A 时,点 P 随之停止运动。连结 PQ,PC,设点 P 的运动时间为t(s)。
(1)当点 Q 在线段 BC 上运动时,BQ 的长为 cm,BP 的长为 cm(均用含 t的代数式表示)。
(2)当 PQ与△ABC的一条边垂直时,求t的值。
(3)在点 Q 从点 C 运动到点 A 的过程中,连结PQ,直接写出 PQ中点经过的路径长。
11.我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高线长的平方,则称这个三角形为“勾股高三角形”,两边交点为勾股顶点。
特例感知
(1)①等腰直角三角形 “勾股高三角形”(填“是”或者“不是”)。
②如图1,已知△ABC为“勾股高三角形”,其中C为勾股顶点,CD 是 AB 边上的高线。若 BD=2AD=2,试求线段CD的长度。
深入探究
(2)如图2,已知△ABC 为“勾股高三角形”,其中C为勾股顶点且CA>CB,CD 是 AB 边上的高线。试探究线段 AD 与CB 的数量关系,并给予证明。
推广应用
(3)如图3,等腰三角形ABC为“勾股高三角形”,其中AB=AC>BC,CD为AB 边上的高线,过点D作BC 边的平行线,与AC 边相交于点 E。若CE=a,试求线段 DE的长度。
题型归类
【典例1】A
【变式1】A
【典例2】(1)①20° ②β=4a-180° (2)
【变式2】(1)略 (2)8
【典例3】略
【变式3】
【典例4】
【变式
【变式 (2)略
【典例5】(1)略 (2)78
【变式5】略
过关训练
1. D 2. B 3.23 4.> 5. 7 6.略 7.略
8.(1)略(2)
10.(1)t 6-t (2)2或4或8 (3)3c m
11.(1)①是 ② (2)AD=CB。证明略 (3)2a
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
