第2章 特殊三角形 秘题加练 2025-2026学年浙教版数学八年级上册(答案不全)
文档属性
| 名称 | 第2章 特殊三角形 秘题加练 2025-2026学年浙教版数学八年级上册(答案不全) |
|
|
| 格式 | docx | ||
| 文件大小 | 467.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 00:00:00 | ||
图片预览




文档简介
秘题加练17 数学思想——对称补缺
2.1图形的轴对称 打卡日期: 实际用时: 分钟
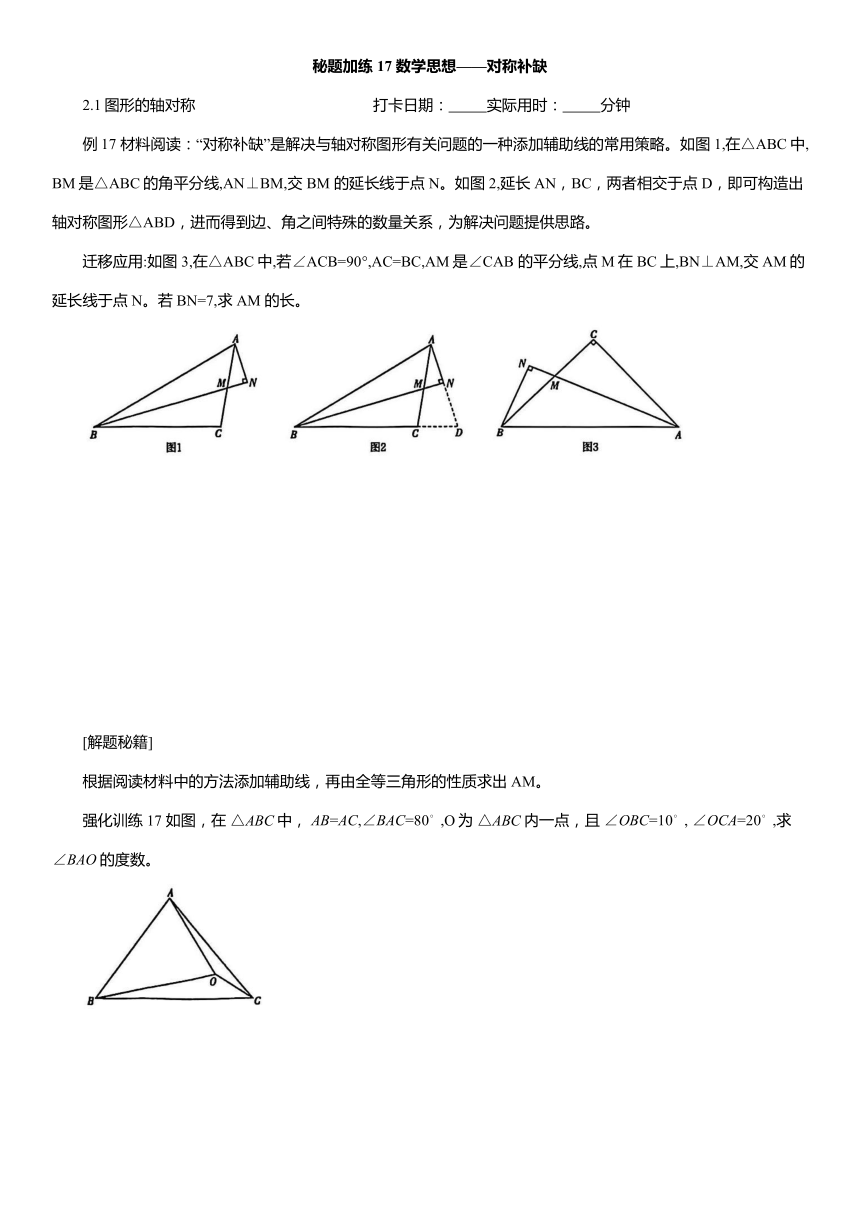
例17 材料阅读:“对称补缺”是解决与轴对称图形有关问题的一种添加辅助线的常用策略。如图1,在△ABC中,BM是△ABC的角平分线,AN⊥BM,交 BM 的延长线于点 N。如图2,延长AN,BC,两者相交于点 D,即可构造出轴对称图形△ABD,进而得到边、角之间特殊的数量关系,为解决问题提供思路。
迁移应用:如图3,在△ABC中,若∠ACB=90°,AC=BC,AM是∠CAB 的平分线,点 M在BC上,BN⊥AM,交AM的延长线于点N。若BN=7,求AM 的长。
[解题秘籍]
根据阅读材料中的方法添加辅助线,再由全等三角形的性质求出AM。
强化训练17 如图,在 中, O为 内一点,且 求 的度数。
秘题加练18 数学思想——等腰三角形中的分类讨论思想
2.2等腰三角形 打卡日期: 实际用时: 分钟
例18 在 中,AB=AC,AC边上的中线BD 把 的周长分成12 cm和15 cm 的两部分,求 各边的长。
[解题秘籍]
由题意可得线段之间的数量关系,进而求出边长。
强化训练18 已知在 中,AB=AC,,AC边上的中线BD 把 分成周长差为 2cm 的两个三角形。已知 的周长为16 cm,求 各边的长。
秘题加练19 等腰三角形的性质
2.3等腰三角形的性质定理 打卡日期: 实际用时: 分钟
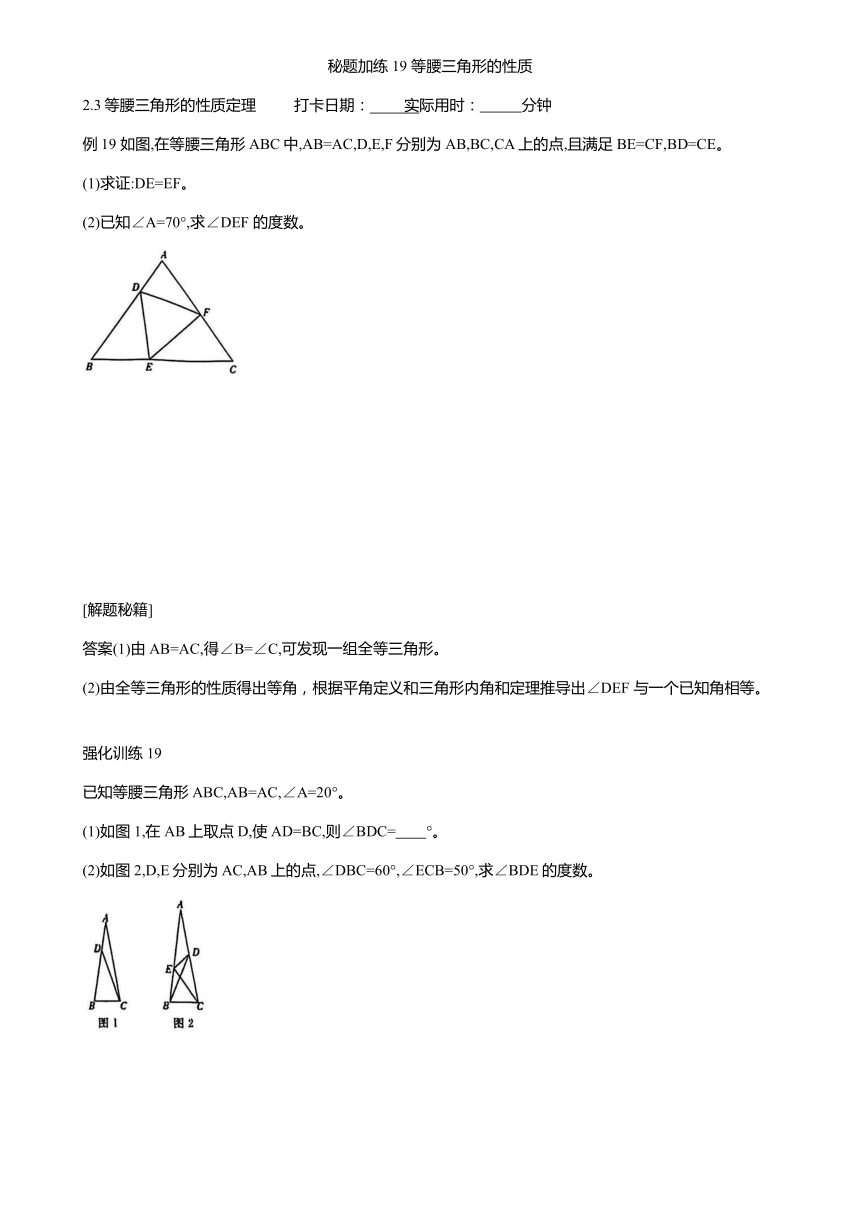
例19 如图,在等腰三角形ABC中,AB=AC,D,E,F分别为AB,BC,CA上的点,且满足BE=CF,BD=CE。
(1)求证:DE=EF。
(2)已知∠A=70°,求∠DEF 的度数。
[解题秘籍]
答案(1)由AB=AC,得∠B=∠C,可发现一组全等三角形。
(2)由全等三角形的性质得出等角,根据平角定义和三角形内角和定理推导出∠DEF 与一个已知角相等。
强化训练19
已知等腰三角形ABC,AB=AC,∠A=20°。
(1)如图1,在AB上取点D,使AD=BC,则∠BDC= °。
(2)如图2,D,E分别为AC,AB上的点,∠DBC=60°,∠ECB=50°,求∠BDE的度数。
秘题加练20 等边三角形的性质与全等三角形的综合
2.3等腰三角形的性质定理 打卡日期: 实际用时: 分钟
例20 (1)如图1,△ABD和△AEC都是等边三角形,求证:BE=DC。
(2)如图2,已知点 F在直线BC 上,∠ABC=60°,以 AF 为边作等边三角形AEF,连结 BE,求证:AB+BF=BE。
[解题秘籍] (1)由等边三角形的性质证明△ADC≌△ABE,即可得到答案。 (2)构造等边三角形,利用(1)中结论可得到答案。
强化训练20 【模型定义】“手拉手模型”是由两个共顶点且顶角相等的等腰三角形构成。在相对位置变化的同时,始终存在一对全等三角形。如果把小等腰三角形的腰看作是小手,大等腰三角形的腰看作大手,两个等腰三角形有公共顶点,类似大手拉着小手。
【模型探究】(1)如图1,若△ACB和△DCE均为等边三角形,点 A,D,E在同一条直线上,连结BE,则∠AEB 的度数为 °,线段BE与AD 之间的数量关系是 。
【模型应用】(2)如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD。
【拓展提高】(3)如图3,在两个等腰直角三角形 ABC和ADE 中,AB=AC,AE=AD,∠BAC=∠DAE=90°,连结BD,CE,两者相交于点 P,则 BD和CE 的数量关系是 ,位置关系是 。
秘题加练21 等腰三角形“三线合一”
2.3等腰三角形的性质定理 打卡日期: 实际用时: 分钟
例21 把下列证明过程补充完整。
已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,CE⊥AB于点E。
求证:∠CAD=∠BCE。
证明:∵AB=AC,
∴∠B=∠ 。
∵AD是BC 边上的中线,
∴AD BC,
∴∠ADC=90°,
∴∠CAD+∠ACB=90°。
∵CE⊥AB,∴∠BEC=90°,
∴∠ +∠B=90°,
∴∠CAD=∠BCE。
[解题秘籍]
在补填证明过程时,要注意由同一个条件可能会推得几个不同的结论,而这些结论都可以用来继续证明,因此为了避免填错,需要结合上下文。
强化训练21 如图,在等腰三角形ABC中,AB=AC=5,AD=4,BC=6。在AB,AC上分别截取AP,AQ,使AP=AQ。再分别以点 P,Q为圆心,以大于 的长为半径作弧,两弧在∠BAC内相交于点 R,作射线 AR,交 BC于点 D。若点 M,N分别是线段AD 和线段AB 上的动点,求BM+MN的最小值。
秘题加练22 等角对等边
2.4等腰三角形的判定定理 打卡日期: 实际用时: 分钟例22 如图,在△ABC中,∠ABC,∠ACB的平分线相交于点F,过点 F作DE∥BC,交AB 于点D,交AC于点E,那么下列结论:①△BDF,△CEF都是等腰三角形;②DE=DB+CE;③AD+DE+AE=AB+AC;④BF=CF。其中所有正确的结论为 (填序号)。
[解题秘籍] 根据角平分线的性质、平行线的性质,借助于等量代换可求出∠DBF=∠DFB,即△BDF是等腰三角形,同理△CEF是等腰三角形,进而利用等腰三角形的性质解答即可。
强化训练22 如图,在△ABC 中,∠BAC的平分线交BC 于点D,P为CA 延长线上一点,过点P 作PE∥AD,分别交AB,BC于F,E两点。
(1)求证:△APF是等腰三角形。
(2)过点C作CH∥AB,交AD的延长线于点H,若CD=DH,请直接写出图中所有的等腰三角形(△APF除外)。
秘题加练23 逆命题与逆定理
2.5逆命题和逆定理 打卡日期: 实际用时: 分钟
例23 如图1,将两个相同的含 30°角的三角尺摆放在一起,可以证得 是等边三角形,于是我们得到:在直角三角形中,如果一个锐角等于 ,那么它所对的直角边等于斜边的一半。交换命题的条件和结论,会得到一个新命题,请写出这个新命题,并判断此命题的真假。若为真命题,请利用图2给出证明(写出已知、求证和证明过程);若为假命题,请说明理由。
[解题秘籍]
参考图1.延长BC至点D,使CD=BC,连结AD,发现 的特殊性,再由 的性质得到结论。
强化训练23 如图,点 分别在等边三角形ABC的三边上,且 求证: 是等边三角形。
小聪在做完课本中的这道题后发现:若把原命题中‘ 的条件与原命题中的 是等边三角形”的结论互换位置,则得到的命题仍是真命题。请你帮助小聪证明他的结论(写出已知、求证和证明过程)。
秘题加练24 与“斜边上的中线”有关的综合题
2.6直角三角形 打卡日期: 实际用时: 分钟
例24 如图,在△ABC中,AD是BC边上的高线,CE是AB 边上的中线,F为CE 的中点,连结DF,已知CD=AE。
(1)若∠BAD=50°,则∠EDB 的度数为 °。
(2)求证:DF⊥CE。
(3)若 求 的值。
[解题秘籍]
答案(1)解在直角三角形中求角度的问题,要能想到斜边上的中线分直角三角形为两个等腰三角形。
(2)发现DF和CE在同一个三角形中,而F又是CE 的中点,容易想到“三线合一”,故想到通过用直角三角形的性质证ED=DC。
(3)利用中线分三角形为面积相等的两部分,找到 和 的面积关系,进而求出 BD与DC之比。
强化训练24 如图1,在锐角三角形ABC中,CD,BE分别是AB,AC边上的高线,M,N分别是线段BC,DE的中点。
(1)求证:
(2)连结 DM,ME。
①若 则
②猜想 与 之间的数量关系,并证明你的猜想。
(3)当 变为钝角时,如图2,上述(1)(2)中的结论是否都成立 若成立,直接回答,不需证明;若不成立,请说明理由。
秘题加练25 直角三角形的判定
2.6直角三角形 打卡日期: 实际用时: 分钟
例25 如图,△ABC是等腰直角三角形,∠ACB=90°,D为AC上一点,延长BC至点E,使CE=CD,连结AE,BD,延长BD交AE 于点F。求证:△BEF是直角三角形。
[解题秘籍]
发现图形中的全等三角形,利用全等三角形的性质证明∠EBF+∠E=90°。
强化训练25
1.如图,在△ABC中,∠A=90°,AB=AC,D为BC 的中点,E,F分别是AB,AC上的点,且BE=AF。求证:△DEF 是等腰直角三角形。
2.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,点E在BC 上,CE=AC,EF⊥CD 于点F。
(1)求证:AD=CF。
(2)连结AE,若G是AE 的中点,连结GD,GF,求证:GD⊥GF。
秘题加练26 勾股定理的应用
2.7探索勾股定理 打卡日期: 实际用时: 分钟
例26 勾股定理有着悠久的历史,它的证明曾引起很多人的兴趣。如图1,以直角三角形的三边为边向外作正方形,西方著名数学家毕达哥拉斯就曾用此图形证明了勾股定理。现把较小的两个正方形纸片按图2所示的方式放置在最大的正方形内,两个较小正方形纸片的重叠部分记为四边形ABCD。若AB=3,求图中阴影部分的面积。
[解题秘籍]
设直角三角形较长直角边长为a,较短直角边长为b,斜边长为 c,由图形可得出阴影部分矩形的长和宽,进而得出阴影部分矩形的面积,再结合勾股定理即可得到结果。本题还可以由勾股定理的面积关系直接看出S田边形ABCD 从而快速得到结果。
强化训练26 阅读理解:
【问题情境】小明用4张全等的直角三角形纸片拼成图1,利用此图可以验证勾股定理吗
【探索新知】从面积的角度思考,不难发现:
大正方形的面积=小正方形的面积-+4个直角三角形的面积。
从而得到等式: 化简证得勾股定理:
【初步运用】(1)如图1,若b=2a,,则小正方形面积:大正方形面积= 。
(2)现将图1中上方的两直角三角形向内折叠,如图2,若(a=4,b=6,,此时空白部分的面积为 。
(3)如图3,将这四个直角三角形紧密地拼接,形成风车状,已知外围轮廓(实线)的周长为24,OC=3,,求该风车状图案的面积。
【迁移运用】(4)如图4,将八个全等的直角三角形紧密地拼接,记图中正方形 ABCD,正方形EF-GH,正方形 MNKT的面积分别为 若 则
秘题加练27 勾股定理的逆定理
2.7探索勾股定理 打卡日期: 实际用时: 分钟
例27 如图,在△ABC中,AB=AC=13cm,,D是边 BC 上一点,BD=5cm,AD=12cm,动点P从点A 出发沿AC以1cm/s的速度向终点C运动,设运动时间为t(s),当BP 的中垂线恰好经过点 D时,求t的值。
[解题秘籍]
利用勾股定理的逆定理得出. 是直角三角形;利用 BP 的中垂线经过点D 及等量代换得到DP=DC,过点D作PC 的垂线DE,利用三角形面积相等得出DE的长,再结合勾股定理即可得到结果。本题应注意分类讨论。
强化训练27 如图,在四边形 ABCD 中, ,试探索以 AB,BC,BD为边,能否组成直角三角形,并说明理由。
秘题加练28 直角三角形全等的判定
2.8直角三角形全等的判定 打卡日期: 实际用时: 分钟
例28 已知AD是△ABC的角平分线, 垂足分别为E,F。
(1)如图1,若BD=CD,求证:BE=CF。
(2)如图2,连结EF,求证:AD垂直平分EF。
[解题秘籍]
(1)先利用角平分线的性质得到DE=DF,再证明
(2)由(1)得点D在EF 的垂直平分线上,再通过证明三角形全等得到点A 在EF 的垂直平分线上,
强化训练28
1.如图,在△ABC中,∠C=90°,D为BC 上一点,E为△ABC外一点,AB=AE,连结AD,DE,DE交AB 于点 F,且 AD平分∠CDE。
(1)用尺规完成以下基本作图:过点A 作DE 的垂线,垂足为 M(不写作法,保留作图痕迹)。
(2)在(1)的条件下,求证:∠BDF=∠EAF(填空)。
证明:∵∠C=90°,∴CA⊥CD。
∵AD平分∠CDE,CA⊥CD,AM⊥DE,
∴ 。
在 Rt△ABC和 Rt△AEM中,
∴Rt△ABC≌Rt△AEM( ),
∴ 。
∵∠BFE=∠B+∠BDF,∠BFE=∠E+∠EAF,
∴∠B+∠BDF= ,
∴∠BDF=∠EAF。
2.如图,在△ABC中,AB=AC,D,E分别是AC,AB上的点,M,N分别是CE,BD上的点,若MA⊥CE,AN⊥BD,AM=AN。求证:
(1)△ABN≌△ACM。
(2)EM=DN。
秘题加练29 再谈截长补短法
第2章 学习任务清单 打卡日期: 实际用时: 分钟
例29 当题目中出现线段的和差关系时,考虑用截长补短法,该类题目中常出现等腰三角形、角平分线等关键词句,要认真留意。
如图,在△ABC中,AD平分∠BAC,交BC于点D,且∠B=2∠C,求证:AB+BD=AC。
截长法:如图1,在 AC上截取AE=AB,连结DE,证明CE=BD即可。
补短法:如图2,延长AB到点 F,使 BF=BD,连结 DF,证明AF=AC即可。
请补全两种方法的证明过程。
[解题秘籍] 在本题中,截长法和补短法的核心都是创造轴对称图形,再利用轴对称带来的众多等量关系进行角度或线段转换,从而解决问题。在三角形中,与轴对称密切相关的就是角平分线。
强化训练29 在△ABC中,∠CAB=2α,且0°<α<30°,AP 平分∠CAB。
(1)如图1,若α=21°,∠ABC=32°,且AP 交BC 于点 P,试探究线段AB,AC与PB 之间的数量关系,并加以证明。
(2)如图2,若∠ABC=60°-α,点 P 在△ABC的内部,且∠CBP=30°,求∠APC 的度数(用含α的代数式表示)。
秘题加练30 几何模型——倍长中线模型
第2章 学习任务清单 打卡日期: 实际用时: 分钟
例30 学习了全等三角形后,我们知道中点在平行线之间的题目通常会用到倍长中线构造“8”字型全等的方法:如图1,已知AB∥CD,连结AD,BC,两者相交于点E,若E为AD的中点,则有△ABE≌△DCE。请利用以上方法解决下列问题。
(1)如图2,为测量河对岸点A 到点B 的距离,过点 B作直线l,并在直线l上依次取点C 和点D,使得AC⊥l,BC=BD。补全图形,指出测量哪条线段就可知道AB的长,并加以证明。
(2)如图3,在△ABC中,D是AC的中点,分别以AB,BC为一条直角边,向外作等腰直角三角形ABE 和BCF,∠ABE=∠CBF=90°,试判断线段 BD与EF 的数量关系并说明理由。
(3)如图4,在 Rt△ABC中,∠ACB=90°,D为AB 的中点,连结CD,过点 D作ED⊥CD,交AC于点E。已知AE=2,BC=5,则CE 的长为 。
[解题秘籍] (1)根据题目中的方法,构造“8”字形全等模型,找到AB的对应边即可。 (2)延长BD至点G,使得. ,连结CG,通过“8”字形全等得到角和边的等量关系,从而发现另一组全等三角形。 (3)延长CD至点 F,使. .连结AF,EF,即可将AE,BC,CE转化到同一个三角形中。
强化训练30 【探索发现】(1)如图1,在 中,D为线段BC 的中点,延长AD至点E,使AD=DE,连结CE。能证明 的依据是 。
【初步应用】(2)如图 2,AD 是 边BC上的中线,E是AC 上一点,BE交AD 于点F。若EF=EA,BF=8,CE=5,求 EF 的长度。
【拓展提升】(3)如图3,在 中,D是BC 的中点, 点E,F分别在AB,AC上,DE 若BE=2,EF=4,求CF 的长。
秘题加练31 等腰三角形中的新定义问题
第2章 学习任务清单 打卡日期: 实际用时: 分钟
例31 在平面内,对于一个等腰三角形,若存在一个点到一条腰两端点的距离相等,且到三角形第三个顶点的距离等于腰长,则我们称这个点为等腰三角形的“双合点”。如图1,在等腰三角形ABC中,AB=AC,且AP=BP,PC=AC,则称点 P 为等腰三角形ABC 的“双合点”。
(1)如图2,在等腰三角形ABC中,AB=AC,请用无刻度的直尺和圆规作出该等腰三角形的一个“双合点”P(保留作图痕迹)。
(2)在等腰三角形 ABC中,AB=AC。
①如图3,当“双合点” P 恰好在边 BC 上,且满足 PC=AC时,求∠BAC的度数。
②当“双合点” P 在边BC 的延长线上时,∠BAC= °。
(3)如图4,在等腰三角形 ABC中,AB=AC,∠BAC=90°,Q为△ABC 内一点,连结 AQ,BQ。当∠CAQ=∠CBQ=15°时,求证:点 Q为等腰三角形ABC 的“双合点”。
[解题秘籍]
(1)根据“双合点”的定义,作一条腰的垂直平分线,以这条腰所对的顶点为圆心,展长为半径画弧交这条腰的垂直平分线于点 P,则点 P 即为所求。
(2)根据“双合点”的定义和等腰三角形的性质,再由等边对等角和三角形的内角和为 解答。
(3)过点 B 作 于点 H,过点 Q作( 于点G,过点 C作( 于点 D,连结 CQ,证明 ,再运用含 角的直角三角形的性质即可解答。
强化训练31
定义:在△ABC中,BC=a,AC=b,AB=c,若a,b,c满足 则称这个三角形为"和谐勾股三角形"。请根据以上定义解决下列问题:
(1)命题“直角三角形都是和谐勾股三角形”是 (填“真”或“假”)命题。
(2)如图1,若等腰三角形ABC 是“和谐勾股三角形”,其中AB=BC,AC>AB,求 的度数。
(3)如图2,在 申,∠B=2∠A,且
①当 时,你能把这个三角形分成两个等腰三角形吗 若能,请在图2中画出分割线,并标注被分割后的两个等腰三角形的顶角度数;若不能,请说明理由。
②请证明 为”和谐勾股三角形”。
秘题加练32 等腰三角形中的探究问题
第2章 学习任务清单 打卡日期: 实际用时: 分钟
例32 综合与实践:小聪与小慧两个同学在学习了“直角三角形全等的判定”后,对数学中重要的学习方法“构造法”展开了课后探究。
【情景再现】如图1,在△ACB 和△A'C'B'中,
下面是用“构造法”证明两个直角三角形全等的部分过程。
证明:如图1,延长BC至点D,使CD=B'C',连结AD。
(已知),∠ACD=Rt∠=∠C',
∴△ADC≌△A'B'C'(SAS),
(全等三角形的对应边相等)。
……
∴△ABC≌△ADC(SSS),
∴△ABC≌△A'B'C'。
【实践解决】(1)请结合“情景再现”的证明过程,把“……”的部分补充完整。
(2)小聪进行了如下的思考:如图2,△ABC和△DCE都是等腰直角三角形,且 连结AD,若. 求AE的长。
(3)小慧结合“构造法”进行了进一步探究:如图3,△MON 是等腰直角三角形, 3是△MON 外一点, 求线段 NP 的长。
[解题秘籍] (1)结合上下文,找到相等的边即可。 (2)由三角形全等证明. ,发现BD在一个直角三角形中。 (3)由(2)中的思路,容易想到在OP 外侧作等腰直角三角形,再利用(2)中的结论易得NP的长。
强化训练32 【教材呈现】如图1 所示为数学教材的部分内容。
【操作发现】(1)如图2,通过作图我们可以发现,此时(即“边边角”对应相等)的两个三角形 全等(填“一定”或“不一定”)。
【探究证明】(2)阅读并补全证明:
已知:如图3,在△ABC和△DEF中,∠B=∠E,AC=DF,∠C+∠F=180°(∠C<∠F)。
求证:AB=DE。
证明:在 BC上取一点G,使AG=AC。
∵AG=AC,∴∠C= 。
又∵∠C+∠F=180°,而∠AGC+∠AGB=180°,
∴∠AGB= 。
∵AC=DF,∴AG= 。
又∵ ,
∴△ABG≌△DEF(AAS),∴AB=DE。
【拓展应用】(3)在△ABC中,AB=AC,点D 在射线BA 上,点E在AC 的延长线上,且BD=CE,连结DE,DE 与BC 边所在的直线相交于点F。
①如图4,当点 D 在线段BA 上时,求证:DF=EF。
②过点 D 作DH⊥BC,交直线 BC 于点 H ,若BC=4,CF=1,则BH的长为 。
【强化训练17】 70°
例18. 10 cm,10 cm,7 cm或8cm ,8cm,1 1 cm
【强化训练18】 6 cm,6 cm,4 cm或
例19. (1)略 (2)55°
【强化训练19】 (1)30 (2)30°
例20. 略
【强化训练20】 (1)60 AD=BE (2)略
(3)BD=CE BD⊥CE
例21. ACB ⊥ BCE
【强化训练21】
例22. ①②③
【强化训练22】 (1)略 (2)△CDH,△ABD,△ACH,△BEF例23.真命题。证明略
【强化训练23】略
例24. (1)40°(2)略 (3)1
【强化训练24】 (1)略
(2)①40 ②猜想: 证明略
(3)结论(1)成立。结论(2)不成立。理由略
例25. 略
【强化训练25】 1.略 2.略
例26. 92
【强化训练26】 (1)5:9 (2)28 (3)24 (4)403
例27. 或13
【强化训练27】以AB,BC,BD为边,能组成直角三角形。理由略
例 28. 略
【强化训练28】
1.(1)略 (2)AC=AM HL ∠B=∠E ∠E+∠EAF
2.略
例29. 略
【强化训练29】 (1)AB-AC=PB。证明略 (2)120°+α例30.(1)补全图形略,测量BM的长就可以知道AB 的长。证明略
理由略
【强化训练30】 (1)SAS (2)3 (
例31. (1)略 (2)①108° ②36 (3)略
【强化训练31】 (1)假 (2)45° (3)①略 ②略
例32. (1)略 (2)3 (3)2
【强化训练32】(1)不一定
(2)∠AGC ∠F DF ∠B=∠E (3)①略 ②1或3
例33. (1)450x+600(15-x)≤7 200
(2)200x+300(15-x)>3200
2.1图形的轴对称 打卡日期: 实际用时: 分钟
例17 材料阅读:“对称补缺”是解决与轴对称图形有关问题的一种添加辅助线的常用策略。如图1,在△ABC中,BM是△ABC的角平分线,AN⊥BM,交 BM 的延长线于点 N。如图2,延长AN,BC,两者相交于点 D,即可构造出轴对称图形△ABD,进而得到边、角之间特殊的数量关系,为解决问题提供思路。
迁移应用:如图3,在△ABC中,若∠ACB=90°,AC=BC,AM是∠CAB 的平分线,点 M在BC上,BN⊥AM,交AM的延长线于点N。若BN=7,求AM 的长。
[解题秘籍]
根据阅读材料中的方法添加辅助线,再由全等三角形的性质求出AM。
强化训练17 如图,在 中, O为 内一点,且 求 的度数。
秘题加练18 数学思想——等腰三角形中的分类讨论思想
2.2等腰三角形 打卡日期: 实际用时: 分钟
例18 在 中,AB=AC,AC边上的中线BD 把 的周长分成12 cm和15 cm 的两部分,求 各边的长。
[解题秘籍]
由题意可得线段之间的数量关系,进而求出边长。
强化训练18 已知在 中,AB=AC,,AC边上的中线BD 把 分成周长差为 2cm 的两个三角形。已知 的周长为16 cm,求 各边的长。
秘题加练19 等腰三角形的性质
2.3等腰三角形的性质定理 打卡日期: 实际用时: 分钟
例19 如图,在等腰三角形ABC中,AB=AC,D,E,F分别为AB,BC,CA上的点,且满足BE=CF,BD=CE。
(1)求证:DE=EF。
(2)已知∠A=70°,求∠DEF 的度数。
[解题秘籍]
答案(1)由AB=AC,得∠B=∠C,可发现一组全等三角形。
(2)由全等三角形的性质得出等角,根据平角定义和三角形内角和定理推导出∠DEF 与一个已知角相等。
强化训练19
已知等腰三角形ABC,AB=AC,∠A=20°。
(1)如图1,在AB上取点D,使AD=BC,则∠BDC= °。
(2)如图2,D,E分别为AC,AB上的点,∠DBC=60°,∠ECB=50°,求∠BDE的度数。
秘题加练20 等边三角形的性质与全等三角形的综合
2.3等腰三角形的性质定理 打卡日期: 实际用时: 分钟
例20 (1)如图1,△ABD和△AEC都是等边三角形,求证:BE=DC。
(2)如图2,已知点 F在直线BC 上,∠ABC=60°,以 AF 为边作等边三角形AEF,连结 BE,求证:AB+BF=BE。
[解题秘籍] (1)由等边三角形的性质证明△ADC≌△ABE,即可得到答案。 (2)构造等边三角形,利用(1)中结论可得到答案。
强化训练20 【模型定义】“手拉手模型”是由两个共顶点且顶角相等的等腰三角形构成。在相对位置变化的同时,始终存在一对全等三角形。如果把小等腰三角形的腰看作是小手,大等腰三角形的腰看作大手,两个等腰三角形有公共顶点,类似大手拉着小手。
【模型探究】(1)如图1,若△ACB和△DCE均为等边三角形,点 A,D,E在同一条直线上,连结BE,则∠AEB 的度数为 °,线段BE与AD 之间的数量关系是 。
【模型应用】(2)如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD。
【拓展提高】(3)如图3,在两个等腰直角三角形 ABC和ADE 中,AB=AC,AE=AD,∠BAC=∠DAE=90°,连结BD,CE,两者相交于点 P,则 BD和CE 的数量关系是 ,位置关系是 。
秘题加练21 等腰三角形“三线合一”
2.3等腰三角形的性质定理 打卡日期: 实际用时: 分钟
例21 把下列证明过程补充完整。
已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,CE⊥AB于点E。
求证:∠CAD=∠BCE。
证明:∵AB=AC,
∴∠B=∠ 。
∵AD是BC 边上的中线,
∴AD BC,
∴∠ADC=90°,
∴∠CAD+∠ACB=90°。
∵CE⊥AB,∴∠BEC=90°,
∴∠ +∠B=90°,
∴∠CAD=∠BCE。
[解题秘籍]
在补填证明过程时,要注意由同一个条件可能会推得几个不同的结论,而这些结论都可以用来继续证明,因此为了避免填错,需要结合上下文。
强化训练21 如图,在等腰三角形ABC中,AB=AC=5,AD=4,BC=6。在AB,AC上分别截取AP,AQ,使AP=AQ。再分别以点 P,Q为圆心,以大于 的长为半径作弧,两弧在∠BAC内相交于点 R,作射线 AR,交 BC于点 D。若点 M,N分别是线段AD 和线段AB 上的动点,求BM+MN的最小值。
秘题加练22 等角对等边
2.4等腰三角形的判定定理 打卡日期: 实际用时: 分钟例22 如图,在△ABC中,∠ABC,∠ACB的平分线相交于点F,过点 F作DE∥BC,交AB 于点D,交AC于点E,那么下列结论:①△BDF,△CEF都是等腰三角形;②DE=DB+CE;③AD+DE+AE=AB+AC;④BF=CF。其中所有正确的结论为 (填序号)。
[解题秘籍] 根据角平分线的性质、平行线的性质,借助于等量代换可求出∠DBF=∠DFB,即△BDF是等腰三角形,同理△CEF是等腰三角形,进而利用等腰三角形的性质解答即可。
强化训练22 如图,在△ABC 中,∠BAC的平分线交BC 于点D,P为CA 延长线上一点,过点P 作PE∥AD,分别交AB,BC于F,E两点。
(1)求证:△APF是等腰三角形。
(2)过点C作CH∥AB,交AD的延长线于点H,若CD=DH,请直接写出图中所有的等腰三角形(△APF除外)。
秘题加练23 逆命题与逆定理
2.5逆命题和逆定理 打卡日期: 实际用时: 分钟
例23 如图1,将两个相同的含 30°角的三角尺摆放在一起,可以证得 是等边三角形,于是我们得到:在直角三角形中,如果一个锐角等于 ,那么它所对的直角边等于斜边的一半。交换命题的条件和结论,会得到一个新命题,请写出这个新命题,并判断此命题的真假。若为真命题,请利用图2给出证明(写出已知、求证和证明过程);若为假命题,请说明理由。
[解题秘籍]
参考图1.延长BC至点D,使CD=BC,连结AD,发现 的特殊性,再由 的性质得到结论。
强化训练23 如图,点 分别在等边三角形ABC的三边上,且 求证: 是等边三角形。
小聪在做完课本中的这道题后发现:若把原命题中‘ 的条件与原命题中的 是等边三角形”的结论互换位置,则得到的命题仍是真命题。请你帮助小聪证明他的结论(写出已知、求证和证明过程)。
秘题加练24 与“斜边上的中线”有关的综合题
2.6直角三角形 打卡日期: 实际用时: 分钟
例24 如图,在△ABC中,AD是BC边上的高线,CE是AB 边上的中线,F为CE 的中点,连结DF,已知CD=AE。
(1)若∠BAD=50°,则∠EDB 的度数为 °。
(2)求证:DF⊥CE。
(3)若 求 的值。
[解题秘籍]
答案(1)解在直角三角形中求角度的问题,要能想到斜边上的中线分直角三角形为两个等腰三角形。
(2)发现DF和CE在同一个三角形中,而F又是CE 的中点,容易想到“三线合一”,故想到通过用直角三角形的性质证ED=DC。
(3)利用中线分三角形为面积相等的两部分,找到 和 的面积关系,进而求出 BD与DC之比。
强化训练24 如图1,在锐角三角形ABC中,CD,BE分别是AB,AC边上的高线,M,N分别是线段BC,DE的中点。
(1)求证:
(2)连结 DM,ME。
①若 则
②猜想 与 之间的数量关系,并证明你的猜想。
(3)当 变为钝角时,如图2,上述(1)(2)中的结论是否都成立 若成立,直接回答,不需证明;若不成立,请说明理由。
秘题加练25 直角三角形的判定
2.6直角三角形 打卡日期: 实际用时: 分钟
例25 如图,△ABC是等腰直角三角形,∠ACB=90°,D为AC上一点,延长BC至点E,使CE=CD,连结AE,BD,延长BD交AE 于点F。求证:△BEF是直角三角形。
[解题秘籍]
发现图形中的全等三角形,利用全等三角形的性质证明∠EBF+∠E=90°。
强化训练25
1.如图,在△ABC中,∠A=90°,AB=AC,D为BC 的中点,E,F分别是AB,AC上的点,且BE=AF。求证:△DEF 是等腰直角三角形。
2.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,点E在BC 上,CE=AC,EF⊥CD 于点F。
(1)求证:AD=CF。
(2)连结AE,若G是AE 的中点,连结GD,GF,求证:GD⊥GF。
秘题加练26 勾股定理的应用
2.7探索勾股定理 打卡日期: 实际用时: 分钟
例26 勾股定理有着悠久的历史,它的证明曾引起很多人的兴趣。如图1,以直角三角形的三边为边向外作正方形,西方著名数学家毕达哥拉斯就曾用此图形证明了勾股定理。现把较小的两个正方形纸片按图2所示的方式放置在最大的正方形内,两个较小正方形纸片的重叠部分记为四边形ABCD。若AB=3,求图中阴影部分的面积。
[解题秘籍]
设直角三角形较长直角边长为a,较短直角边长为b,斜边长为 c,由图形可得出阴影部分矩形的长和宽,进而得出阴影部分矩形的面积,再结合勾股定理即可得到结果。本题还可以由勾股定理的面积关系直接看出S田边形ABCD 从而快速得到结果。
强化训练26 阅读理解:
【问题情境】小明用4张全等的直角三角形纸片拼成图1,利用此图可以验证勾股定理吗
【探索新知】从面积的角度思考,不难发现:
大正方形的面积=小正方形的面积-+4个直角三角形的面积。
从而得到等式: 化简证得勾股定理:
【初步运用】(1)如图1,若b=2a,,则小正方形面积:大正方形面积= 。
(2)现将图1中上方的两直角三角形向内折叠,如图2,若(a=4,b=6,,此时空白部分的面积为 。
(3)如图3,将这四个直角三角形紧密地拼接,形成风车状,已知外围轮廓(实线)的周长为24,OC=3,,求该风车状图案的面积。
【迁移运用】(4)如图4,将八个全等的直角三角形紧密地拼接,记图中正方形 ABCD,正方形EF-GH,正方形 MNKT的面积分别为 若 则
秘题加练27 勾股定理的逆定理
2.7探索勾股定理 打卡日期: 实际用时: 分钟
例27 如图,在△ABC中,AB=AC=13cm,,D是边 BC 上一点,BD=5cm,AD=12cm,动点P从点A 出发沿AC以1cm/s的速度向终点C运动,设运动时间为t(s),当BP 的中垂线恰好经过点 D时,求t的值。
[解题秘籍]
利用勾股定理的逆定理得出. 是直角三角形;利用 BP 的中垂线经过点D 及等量代换得到DP=DC,过点D作PC 的垂线DE,利用三角形面积相等得出DE的长,再结合勾股定理即可得到结果。本题应注意分类讨论。
强化训练27 如图,在四边形 ABCD 中, ,试探索以 AB,BC,BD为边,能否组成直角三角形,并说明理由。
秘题加练28 直角三角形全等的判定
2.8直角三角形全等的判定 打卡日期: 实际用时: 分钟
例28 已知AD是△ABC的角平分线, 垂足分别为E,F。
(1)如图1,若BD=CD,求证:BE=CF。
(2)如图2,连结EF,求证:AD垂直平分EF。
[解题秘籍]
(1)先利用角平分线的性质得到DE=DF,再证明
(2)由(1)得点D在EF 的垂直平分线上,再通过证明三角形全等得到点A 在EF 的垂直平分线上,
强化训练28
1.如图,在△ABC中,∠C=90°,D为BC 上一点,E为△ABC外一点,AB=AE,连结AD,DE,DE交AB 于点 F,且 AD平分∠CDE。
(1)用尺规完成以下基本作图:过点A 作DE 的垂线,垂足为 M(不写作法,保留作图痕迹)。
(2)在(1)的条件下,求证:∠BDF=∠EAF(填空)。
证明:∵∠C=90°,∴CA⊥CD。
∵AD平分∠CDE,CA⊥CD,AM⊥DE,
∴ 。
在 Rt△ABC和 Rt△AEM中,
∴Rt△ABC≌Rt△AEM( ),
∴ 。
∵∠BFE=∠B+∠BDF,∠BFE=∠E+∠EAF,
∴∠B+∠BDF= ,
∴∠BDF=∠EAF。
2.如图,在△ABC中,AB=AC,D,E分别是AC,AB上的点,M,N分别是CE,BD上的点,若MA⊥CE,AN⊥BD,AM=AN。求证:
(1)△ABN≌△ACM。
(2)EM=DN。
秘题加练29 再谈截长补短法
第2章 学习任务清单 打卡日期: 实际用时: 分钟
例29 当题目中出现线段的和差关系时,考虑用截长补短法,该类题目中常出现等腰三角形、角平分线等关键词句,要认真留意。
如图,在△ABC中,AD平分∠BAC,交BC于点D,且∠B=2∠C,求证:AB+BD=AC。
截长法:如图1,在 AC上截取AE=AB,连结DE,证明CE=BD即可。
补短法:如图2,延长AB到点 F,使 BF=BD,连结 DF,证明AF=AC即可。
请补全两种方法的证明过程。
[解题秘籍] 在本题中,截长法和补短法的核心都是创造轴对称图形,再利用轴对称带来的众多等量关系进行角度或线段转换,从而解决问题。在三角形中,与轴对称密切相关的就是角平分线。
强化训练29 在△ABC中,∠CAB=2α,且0°<α<30°,AP 平分∠CAB。
(1)如图1,若α=21°,∠ABC=32°,且AP 交BC 于点 P,试探究线段AB,AC与PB 之间的数量关系,并加以证明。
(2)如图2,若∠ABC=60°-α,点 P 在△ABC的内部,且∠CBP=30°,求∠APC 的度数(用含α的代数式表示)。
秘题加练30 几何模型——倍长中线模型
第2章 学习任务清单 打卡日期: 实际用时: 分钟
例30 学习了全等三角形后,我们知道中点在平行线之间的题目通常会用到倍长中线构造“8”字型全等的方法:如图1,已知AB∥CD,连结AD,BC,两者相交于点E,若E为AD的中点,则有△ABE≌△DCE。请利用以上方法解决下列问题。
(1)如图2,为测量河对岸点A 到点B 的距离,过点 B作直线l,并在直线l上依次取点C 和点D,使得AC⊥l,BC=BD。补全图形,指出测量哪条线段就可知道AB的长,并加以证明。
(2)如图3,在△ABC中,D是AC的中点,分别以AB,BC为一条直角边,向外作等腰直角三角形ABE 和BCF,∠ABE=∠CBF=90°,试判断线段 BD与EF 的数量关系并说明理由。
(3)如图4,在 Rt△ABC中,∠ACB=90°,D为AB 的中点,连结CD,过点 D作ED⊥CD,交AC于点E。已知AE=2,BC=5,则CE 的长为 。
[解题秘籍] (1)根据题目中的方法,构造“8”字形全等模型,找到AB的对应边即可。 (2)延长BD至点G,使得. ,连结CG,通过“8”字形全等得到角和边的等量关系,从而发现另一组全等三角形。 (3)延长CD至点 F,使. .连结AF,EF,即可将AE,BC,CE转化到同一个三角形中。
强化训练30 【探索发现】(1)如图1,在 中,D为线段BC 的中点,延长AD至点E,使AD=DE,连结CE。能证明 的依据是 。
【初步应用】(2)如图 2,AD 是 边BC上的中线,E是AC 上一点,BE交AD 于点F。若EF=EA,BF=8,CE=5,求 EF 的长度。
【拓展提升】(3)如图3,在 中,D是BC 的中点, 点E,F分别在AB,AC上,DE 若BE=2,EF=4,求CF 的长。
秘题加练31 等腰三角形中的新定义问题
第2章 学习任务清单 打卡日期: 实际用时: 分钟
例31 在平面内,对于一个等腰三角形,若存在一个点到一条腰两端点的距离相等,且到三角形第三个顶点的距离等于腰长,则我们称这个点为等腰三角形的“双合点”。如图1,在等腰三角形ABC中,AB=AC,且AP=BP,PC=AC,则称点 P 为等腰三角形ABC 的“双合点”。
(1)如图2,在等腰三角形ABC中,AB=AC,请用无刻度的直尺和圆规作出该等腰三角形的一个“双合点”P(保留作图痕迹)。
(2)在等腰三角形 ABC中,AB=AC。
①如图3,当“双合点” P 恰好在边 BC 上,且满足 PC=AC时,求∠BAC的度数。
②当“双合点” P 在边BC 的延长线上时,∠BAC= °。
(3)如图4,在等腰三角形 ABC中,AB=AC,∠BAC=90°,Q为△ABC 内一点,连结 AQ,BQ。当∠CAQ=∠CBQ=15°时,求证:点 Q为等腰三角形ABC 的“双合点”。
[解题秘籍]
(1)根据“双合点”的定义,作一条腰的垂直平分线,以这条腰所对的顶点为圆心,展长为半径画弧交这条腰的垂直平分线于点 P,则点 P 即为所求。
(2)根据“双合点”的定义和等腰三角形的性质,再由等边对等角和三角形的内角和为 解答。
(3)过点 B 作 于点 H,过点 Q作( 于点G,过点 C作( 于点 D,连结 CQ,证明 ,再运用含 角的直角三角形的性质即可解答。
强化训练31
定义:在△ABC中,BC=a,AC=b,AB=c,若a,b,c满足 则称这个三角形为"和谐勾股三角形"。请根据以上定义解决下列问题:
(1)命题“直角三角形都是和谐勾股三角形”是 (填“真”或“假”)命题。
(2)如图1,若等腰三角形ABC 是“和谐勾股三角形”,其中AB=BC,AC>AB,求 的度数。
(3)如图2,在 申,∠B=2∠A,且
①当 时,你能把这个三角形分成两个等腰三角形吗 若能,请在图2中画出分割线,并标注被分割后的两个等腰三角形的顶角度数;若不能,请说明理由。
②请证明 为”和谐勾股三角形”。
秘题加练32 等腰三角形中的探究问题
第2章 学习任务清单 打卡日期: 实际用时: 分钟
例32 综合与实践:小聪与小慧两个同学在学习了“直角三角形全等的判定”后,对数学中重要的学习方法“构造法”展开了课后探究。
【情景再现】如图1,在△ACB 和△A'C'B'中,
下面是用“构造法”证明两个直角三角形全等的部分过程。
证明:如图1,延长BC至点D,使CD=B'C',连结AD。
(已知),∠ACD=Rt∠=∠C',
∴△ADC≌△A'B'C'(SAS),
(全等三角形的对应边相等)。
……
∴△ABC≌△ADC(SSS),
∴△ABC≌△A'B'C'。
【实践解决】(1)请结合“情景再现”的证明过程,把“……”的部分补充完整。
(2)小聪进行了如下的思考:如图2,△ABC和△DCE都是等腰直角三角形,且 连结AD,若. 求AE的长。
(3)小慧结合“构造法”进行了进一步探究:如图3,△MON 是等腰直角三角形, 3是△MON 外一点, 求线段 NP 的长。
[解题秘籍] (1)结合上下文,找到相等的边即可。 (2)由三角形全等证明. ,发现BD在一个直角三角形中。 (3)由(2)中的思路,容易想到在OP 外侧作等腰直角三角形,再利用(2)中的结论易得NP的长。
强化训练32 【教材呈现】如图1 所示为数学教材的部分内容。
【操作发现】(1)如图2,通过作图我们可以发现,此时(即“边边角”对应相等)的两个三角形 全等(填“一定”或“不一定”)。
【探究证明】(2)阅读并补全证明:
已知:如图3,在△ABC和△DEF中,∠B=∠E,AC=DF,∠C+∠F=180°(∠C<∠F)。
求证:AB=DE。
证明:在 BC上取一点G,使AG=AC。
∵AG=AC,∴∠C= 。
又∵∠C+∠F=180°,而∠AGC+∠AGB=180°,
∴∠AGB= 。
∵AC=DF,∴AG= 。
又∵ ,
∴△ABG≌△DEF(AAS),∴AB=DE。
【拓展应用】(3)在△ABC中,AB=AC,点D 在射线BA 上,点E在AC 的延长线上,且BD=CE,连结DE,DE 与BC 边所在的直线相交于点F。
①如图4,当点 D 在线段BA 上时,求证:DF=EF。
②过点 D 作DH⊥BC,交直线 BC 于点 H ,若BC=4,CF=1,则BH的长为 。
【强化训练17】 70°
例18. 10 cm,10 cm,7 cm或8cm ,8cm,1 1 cm
【强化训练18】 6 cm,6 cm,4 cm或
例19. (1)略 (2)55°
【强化训练19】 (1)30 (2)30°
例20. 略
【强化训练20】 (1)60 AD=BE (2)略
(3)BD=CE BD⊥CE
例21. ACB ⊥ BCE
【强化训练21】
例22. ①②③
【强化训练22】 (1)略 (2)△CDH,△ABD,△ACH,△BEF例23.真命题。证明略
【强化训练23】略
例24. (1)40°(2)略 (3)1
【强化训练24】 (1)略
(2)①40 ②猜想: 证明略
(3)结论(1)成立。结论(2)不成立。理由略
例25. 略
【强化训练25】 1.略 2.略
例26. 92
【强化训练26】 (1)5:9 (2)28 (3)24 (4)403
例27. 或13
【强化训练27】以AB,BC,BD为边,能组成直角三角形。理由略
例 28. 略
【强化训练28】
1.(1)略 (2)AC=AM HL ∠B=∠E ∠E+∠EAF
2.略
例29. 略
【强化训练29】 (1)AB-AC=PB。证明略 (2)120°+α例30.(1)补全图形略,测量BM的长就可以知道AB 的长。证明略
理由略
【强化训练30】 (1)SAS (2)3 (
例31. (1)略 (2)①108° ②36 (3)略
【强化训练31】 (1)假 (2)45° (3)①略 ②略
例32. (1)略 (2)3 (3)2
【强化训练32】(1)不一定
(2)∠AGC ∠F DF ∠B=∠E (3)①略 ②1或3
例33. (1)450x+600(15-x)≤7 200
(2)200x+300(15-x)>3200
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
