第5章 一次函数 秘题加练2025-2026学年浙教版数学八年级上册(答案不全)
文档属性
| 名称 | 第5章 一次函数 秘题加练2025-2026学年浙教版数学八年级上册(答案不全) |

|
|
| 格式 | docx | ||
| 文件大小 | 190.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 00:00:00 | ||
图片预览




文档简介
秘题加练47 常量与变量
5.1常量与变量 打卡日期: 实际用时: 分钟
例 47 某数学兴趣小组在一组课题学习活动中以“钟表上时针与分针的重合时刻”为课题展开了研究。
【问题提出】如图所示为该钟表的简化平面示意图。设时针、分针所在直线在同一平面内,直线l表示钟表的铅垂轴线。在1:00~1:15 之间求时针与分针的重合时刻。
【问题探究】设钟表中心为点O,表示“12”的点为A,表示“1”的点为 B,表示“3”的点为 C,表示“6”的点为 D,下面是小颖同学的研究过程:
解题思路:建立数量关系求解。
(1)设1:00后再经过x(min)(0≤x≤15),时针、分针与OA 所成夹角的度数分别为. 直接写出y ,y 与x之间的关系式。
【问题解决】(2)请按照小颖的思路解答此问题。
【问题拓展】(3)求该钟表在1:15~1:30之间,时针与分针所在直线互相垂直的时刻。
[解题秘籍]
(1)根据分针每分钟转( 时针每分钟转 结合题意列关系式。
(2)令 列方程求解。
(3)根据(1)(2)中的方法求解。
强化训练47 某校门口道路中间的隔离护栏平面示意图如图所示,每根立柱宽为0.2米,立柱间距为3 米。
经测量发现立柱根数与护栏总长度(单位:米)之间的对应数据如下表(不完整):
立柱根数 1 2 3 4 5
护栏总长度/米 0.2 3.4 9.8
(1)将表格补充完整。
(2)设有x根立柱,护栏总长度为y米,则y与x 之间的关系式为 。
(3)求护栏总长度为93米时,立柱的根数。
秘题加练48 动点问题的函数图象
5.2 认识函数 打卡日期: 实际用时: 分钟
例48 如图1,在长方形ABCD中,E 是边AD 上一点,且AE=6 cm,点 P 从点B 出发,沿折线BE-ED-DC匀速运动,运动到点 C停止。已知点 P 的运动速度为2cm/s,运动时间为t(s),△BPC的面积为 y关于t 的函数图象如图2所示,给出下列结论:①a=7;②b=10;③BE=BC;④当t=3时,△PCD 为等腰三角形;⑤当t=10时,y=12。其中正确的是 (填序号)。
[解题秘籍]
先通过r=5,y=40 计算出 BC 的长,则DE的长即可求出,根据DE的长计算a 的值,b的值可以通过整个运动路程除以速度求得,当t=10 时,找到点 P 的位置,计算△BPC的面积即可得到y的值。
强化训练48
1.如图1,在△ABC中,动点 P 从点A 出发,沿折线AB→BC→CA匀速运动至点A 后停止。设点P 的运动路程为x,线段AP的长度为y,图2是y与x的函数关系的大致图象,其中F为曲线 DE的最低点,则△ABC的高线CG 的长为 。
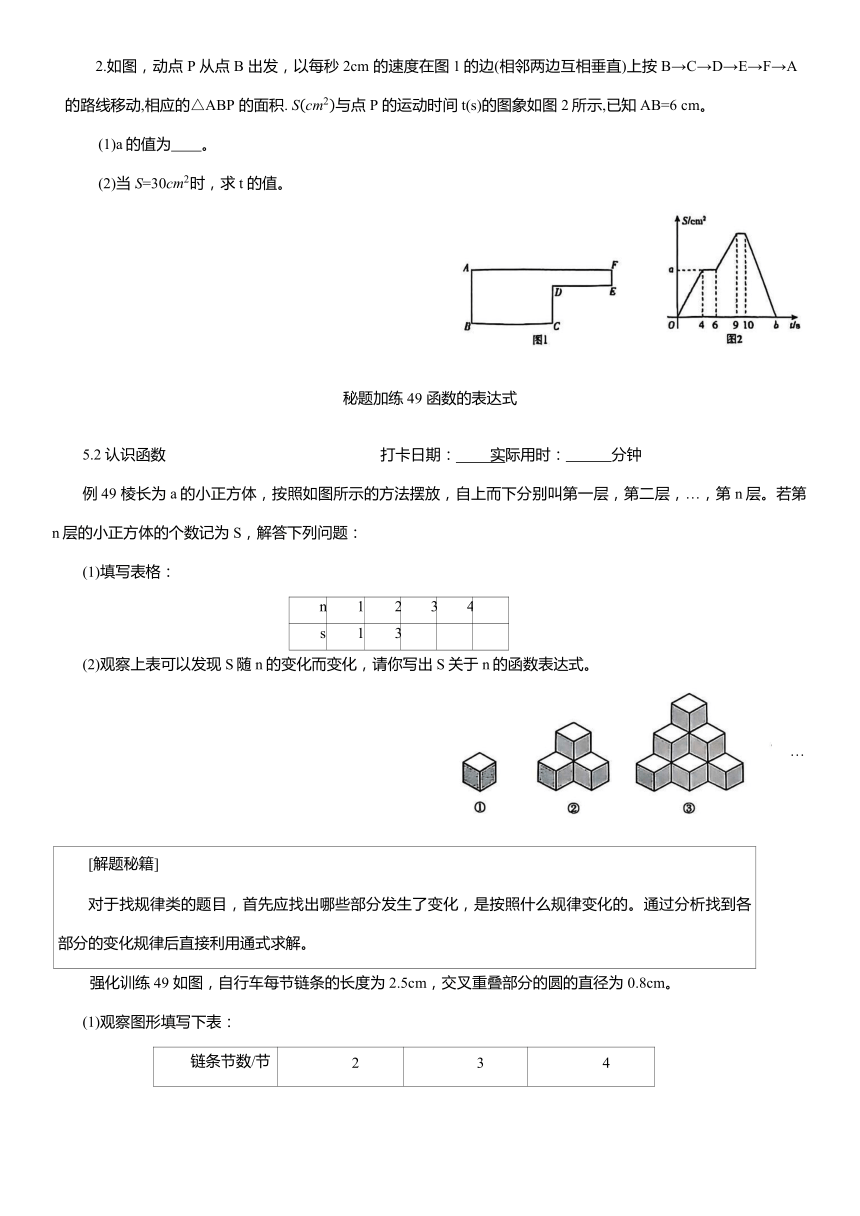
2.如图,动点 P 从点B 出发,以每秒2cm 的速度在图1的边(相邻两边互相垂直)上按 B→C→D→E→F→A 的路线移动,相应的△ABP 的面积. 与点 P 的运动时间t(s)的图象如图2所示,已知AB=6 cm。
(1)a的值为 。
(2)当 时,求t 的值。
秘题加练49 函数的表达式
5.2 认识函数 打卡日期: 实际用时: 分钟
例49 棱长为a的小正方体,按照如图所示的方法摆放,自上而下分别叫第一层,第二层,…,第n层。若第n层的小正方体的个数记为S,解答下列问题:
(1)填写表格:
n 1 2 3 4
s 1 3
(2)观察上表可以发现S随n的变化而变化,请你写出S关于n的函数表达式。
…
[解题秘籍] 对于找规律类的题目,首先应找出哪些部分发生了变化,是按照什么规律变化的。通过分析找到各部分的变化规律后直接利用通式求解。
强化训练49 如图,自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm。
(1)观察图形填写下表:
链条节数/节 2 3 4
链条长度/cm
(2)如果x节链条的总长度是y,求y与x之间的关系式。
(3)如果一辆某种型号自行车的链条(安装前)由80节这样的链条组成,那么这根链条完成连接(安装到自行车上)后,它的周长是多少厘米
秘题加练50 用待定系数法求一次函数的表达式
5.3一次函数的意义 打卡日期: 实际用时: 分钟
例50 已知y是x的一次函数,当x=3时,y=1;当x=-2时,y=-4,,求这个一次函数的表达式。
[解题秘籍]
通过待定系数法求一次函数的表达式。
强化训练50
1.已知y是关于x 的一次函数,且当x=1时,y=-4;当x=2时,y=-6。
(1)求y关于x 的函数表达式。
(2)若-22.已知y-6与2x-3成正比例,且当.x=3时,y=12。求:
(1)y关于x的函数表达式。
(2)当.x=5时,y的值。
3.已知y是关于x 的一次函数,且当.x=3时,y=-2;当x=2时,y=-3。求:
(1)这个一次函数的表达式。
(2)当x=-3时,函数y的值。
(3)当y=2时,自变量x的值。
(4)当y>1时,自变量x的取值范围。
秘题加练51 数形结合——根据图象求一次函数的表达式
5.4一次函数的图象与性质 打卡日期: 实际用时: 分钟
例51 如图,在平面直角坐标系中,一次函数y=kx+5(k≠0)的图象 分别与x轴、y轴相交于A,B两点,正比例函数的图象 与l 相交于点C(2,4)。
(1)求k的值及直线l 的表达式。
(2)若 M是直线l 上一点,连结 OM,当 的面积是 的面积的2倍时,求点 M 的坐标。
[解题秘籍]
(1)直线 与 相交于点C,即点C既在 上,也在 上,利用待定系数法即可求解。
(2)将 和 中的OB边看作底,则点C和点M到OB 的距离,即点 C和点 M 的横坐标的绝对值即为高,再由两个三角形的面积关系求解。
强化训练51 如图,直线y=x+4分别交x轴、y轴于点A,B。直线 经过点B,交x轴于点C。
(1)求b的值和OA,OC的长。
(2)在 BC的延长线上取点 D,使DC=BC,过点 D 作 轴,交AB的延长线于点 E,记 的面积为 的面积为 求 的值。
秘题加练52 分类讨论———一次函数的区间最值问题
5.4一次函数的图象与性质
例52 若一次函数 y= kx+5(k≠0)在-1≤x≤4范围内有最大值17,求k的值。
[解题秘籍] 分两种情况:①若k<0,则当x=-1时,y有最大值17,代入表达式求解;②若k>0,则当x=4时,y有最大值17,代入表达式求解。
强化训练52 已知一次函数y= kx-k+2(k为常数,且k≠0)。
(1)若点(-1,3)在一次函数y= kx-k+2的图象上。
①求k的值。
②设 P=y+x,则当-2≤x≤5时,求 P 的最大值。
(2)若当m-3≤x≤m时,函数有最大值M,最小值 N,且M-N=6,求此时一次函数y的表达式。
秘题加练53 一次函数的应用(一)
5.5一次函数的简单应用 打卡日期: 实际用时: 分钟
例53 某地举办大型活动,该活动纪念品迅速成为热销商品。下表是某商店甲、乙两种活动纪念品的进价和售价:
商品价格 甲 乙
进价/(元/个) 40 100
售价/(元/个) 45 110
(1)该店第一次用3800元购进的甲、乙两种纪念品,售完后共获毛利润400元[毛利润=(售价一进价)×销售量]。该店第一次购进的甲、乙两种纪念品分别为多少个
(2)根据(1)中的销售情况,该店计划第二次进货时,在第一次进货量的基础上增加甲种纪念品的购进量,减少乙种纪念品的购进量,并且甲种纪念品增加的数量是乙种纪念品减少的数量的3倍。已知每种纪念品的进价、售价都不变,设毛利润为w元,乙种纪念品减少的数量为m个。
①求 w关于m 的函数表达式。
②若第二次进货的总资金不超过4000元,则全部销售后获得的最大毛利润是多少
[解题秘籍]
(1)设该店第一次购进的甲种纪念品有x个,乙种纪念品有y个,根据题意列出关于x,y的二元一次方程组。
(2)把题目中陈述的数量关系转化成数学式子即是函数表达式;通过总资金不超过4 000元,求出m 的取伤范围。再由函数的性质求出最值。
强化训练53 杨梅是某地重要的农业经济产品。请根据提供的材料解决问题。
探究杨梅的销售利润
材料一 某商贸公司经销甲、乙两个品种的杨梅,甲品种杨梅的进价为16元/斤,乙品种杨梅的进货总金额y(元)与进货量x(斤)在x≥10时满足的关系如图所示。经过试销,在H市销售甲、乙两个品种杨梅的售价分别定为20元/斤和25元/斤。
材料二 某日,该商贸公司收购了甲、乙两个品种的杨梅共1000斤,其中乙品种的收购量不低于200斤,且不高于500斤。
材料三 杨梅运到 H 市,商场发现顾客对甲、乙两个品种杨梅都很喜欢,于是决定把两种杨梅按同样的价格销售,并适当让利给消费者。
问题解决
任务一 (1)已知E(50,1100),F(100,2 100),求图中直线EF的函数表达式。
任务二 (2)若从收购点运到商场的其他各种费用还需要1800元,收购的杨梅能够全部卖完,设销售完甲、乙两个品种的杨梅所获总利润为w元(利润=销售额一进货金额一其他费用)。求总利润w(元)与乙品种杨梅的进货量x(斤)之间的函数关系式,并为该商贸公司设计出获得最大利润的收购方案。
任务三 (3)在任务二设计的收购方案的基础上,商场把任务二中的最大利润的 让利给消费者。若此时甲、乙两种杨梅的售价均定为每斤a元,求a的值(结果保留整数)。
秘题加练54 数形结合——一次函数与二元一次方程组
5.5一次函数的简单应用 打卡日期: 实际用时: 分钟
例54 如图,已知函数y=x+1和.y=ax+3(a≠0)的图象相交于点 P,点P 的横坐标为1。
(1)关于x,y的方程组 的解是 。
(2)a的值为 。
(3)求出函数y=x+1和y=ax+3的图象与x轴围成的几何图形的面积。
[解题秘籍]
由一次函数与二元一次方程组的联系知,方程组的解就是两个相应的一次函数图象的交点坐标的值。
强化训练54 【了解概念】已知函数 是自变量x的函数,当 时,称函数 为函数y 的“倍差函数”。在平面直角坐标系中,对于函数 y 图象上任意一点A(m,n),称点.B(m,2n-m)为点 A 关于函数. 的“倍差点”,则点 B 在函数y 的“倍差函数”的图象上。
【理解运用】例如:函数 当 时,称函数 是函数 的“倍差函数”。在平面直角坐标系中,函数 图象上任意一点A(m,n),点B(m,2n-m)为点A 关于函数 的“倍差点”,则点 B在函数 的“倍差函数 的图象上。
(1)求函数 的“倍差函数 的表达式。
(2)点 P(m,n)在函数. 的图象上,点P 关于函数 的“倍差点”为Q,若点 Q与点 P 的纵坐标的和为-2,求点 P 的坐标。
【拓展提升】(3)在(2)的条件下, 的“倍差函数”的图象交y轴于点 T,已知点A(t,t),B(t+1,t+2)。若直线AB与 有交点,求t的取值范围。
秘题加练55 一次函数的应用(二)
第5章 学习任务清单 打卡日期: 实际用时: 分钟
例55 小明和小丽相约周末一起去登山锻炼,沿着同一条路线,小丽先开始,并一直匀速登山。5分钟后,小明开始,小明中途休息了两次,每次休息后,登山速度增加5米/分,以便追上小丽,小丽的速度与小明的第一段速度相同。小明和小丽的登山信息如表所示,距离地面的高度y(米)与小丽的登山时间x(分)的函数关系如图所示。
时间 登山阶段 登山速度 登山高度
小丽 8:00至9:00 不分段 v 600米
小明 8:05至8:50 第一段 v 100米
第一次休息
第二段 v+5 200米
第二次休息
第三段 v+10 300米
(1)求小丽的登山速度v。
(2)求小明两次休息时间的总和。
(3)小明第二次休息后,在a 分钟时两人登山高度相等,求a 的值。
[解题秘籍]
(1)小丽的登山速度=小丽的登山路程÷小丽的登山时间。
(2)根据题中朗络的表格中的数据计算由除休息外小明登山的时间及小明竖山忌用时,即可得到小明固次休息时词的总和。
(3)两人登山高度相等,赌相等关系为:小丽昼山的速度×登山的时间a=300+小明第三段昼山的速度×(a一两次休息总用时一推迟出发的S分钟一登第一段山用时一整第二段山用时),把相关数值代入计算即可,
强化训练55 A,B两地相距290 千米,早上9:00,甲货车从 A 地出发匀速将一批物资运往B地,行驶一段路程后出现故障,即刻停车与B地联系。B地收到消息后立即派乙货车从B 地出发匀速去接运甲货车上的物资,乙货车遇到甲货车后,用了30分钟将物资从甲货车搬运到乙货车上,随后开往B地,两辆货车离开各自出发地的路程y(千米)与甲货车出发的时间x(时)的函数关系如图所示。
(1)直接写出甲货车、乙货车的速度。
(2)求乙货车在未遇到甲货车时,它离开出发地的路程y(千米)关于甲货车出发的时间x(时)的函数表达式。
(3)因实际需要,要求乙货车到达B地的时间比甲货车按原来的速度正常到达B 地的时间最多晚1个小时,问乙货车返回B地的速度至少为多少
秘题加练56 一次函数的综合
第5章 学习任务清单 打卡日期: 实际用时: 分钟
例56 如图,直线 y=x+4与x轴、y轴分别相交于点A,B,P 是射线BO上的动点(不与点 B重合),过点 B 作直线AP 的垂线,交x轴于点Q,垂足为C,连结OC。
(1)当点 P 在线段 BO 上时。
①求证:△AOP≌△BOQ。
②若 P 为BO 的中点,求△OCQ 的面积。
(2)在点 P 的运动过程中,是否存在某一位置,使得△OCQ是以OQ 为底的等腰三角形 若存在,求点 P 的坐标;若不存在,请说明理由。
[解题秘籍]
(1)由图象可得出OA=OB,由垂直关系可得出
(2)可求得直线AC和BQ 的表达式,进而求得点C 的坐标。
答案(3)当点 P 在线段OB 上时,可推出OC=BC=CQ,此时C是BQ 的中点,进而得出AQ=AB. 当点 P 在 BO的延长线上时,同理得出结果。
强化训练56 如图1,直线y=kx+1(k>0)分别与x轴,y轴相交于A,B两点,直线 分别与x轴,y轴相交于C,D两点,两条直线相交于点 E。
(1)点C的坐标为 ,点A 的坐标为 (点A 的坐标用含k 的代数式表示)。
(2)若点 A 关于 y轴的对称点.A'恰好落在 的内部,求k的取值范围。
(3)如图2,若D为CE 的中点,Q为直线AB 上一点,连结 DQ,记点 E关于直线DQ 的对称点为 请问:是否存在点Q,使得点E'恰好落在直线CD 上方的坐标轴上 若存在,请求出点 Q 的坐标;若不存在,请说明理由。
【强化训练47】 (1)6.6 13 (2)y=3.2x-3 (3)30
例48. ①③④
【强化训练48】
2.(1)24(2)7或12
例49.(1)6 10
【强化训练49】(1)4.2 5.9 7.6 (2)y=1.7x+0.8(3)136 cm
例50. y=x-2
【强化训练50】
1.(1)y=-2x-2 (2)-102.(1)y=4x (2)20
3.(1)y=x-5 (2)-8 (3)7 (4)x>6
例51.
(2)(4,3)或(-4,7)
【强化训练51】(1)b=4,OA=4,OC=3 (2)
例52. — 12或3
【强化训练52】(1)①- ②5(2)y=2x或y=-2x+4
例53.(1)甲种纪念品20个,乙种纪念品30个
(2)①w=5m+400(m>0且m为整数) ②450元
【强化训练53】 (1)y=20x+100
(2)w=x+2 100(200≤x≤500) (3)22
例54.(1)(t)y=2(2)-1 (3)4
【强化训练54】((1)y =x-4 (2)(2,0) (3)-4例55. (1)10 米/分(2) 分钟 (3)40
【强化训练55】
(1)甲货车的速度是60千米/时,乙货车的速度是100 千米/时
(2)y=100x-150(1.5≤x≤3.5) 千米/时
例56.(1)①略②
(2)存在。点 P 的坐标为(0,4 -4)或(
【强化训练56】(1)(4,0) (- ,0) (2)k>
(3)存在。点Q的坐标为 或
5.1常量与变量 打卡日期: 实际用时: 分钟
例 47 某数学兴趣小组在一组课题学习活动中以“钟表上时针与分针的重合时刻”为课题展开了研究。
【问题提出】如图所示为该钟表的简化平面示意图。设时针、分针所在直线在同一平面内,直线l表示钟表的铅垂轴线。在1:00~1:15 之间求时针与分针的重合时刻。
【问题探究】设钟表中心为点O,表示“12”的点为A,表示“1”的点为 B,表示“3”的点为 C,表示“6”的点为 D,下面是小颖同学的研究过程:
解题思路:建立数量关系求解。
(1)设1:00后再经过x(min)(0≤x≤15),时针、分针与OA 所成夹角的度数分别为. 直接写出y ,y 与x之间的关系式。
【问题解决】(2)请按照小颖的思路解答此问题。
【问题拓展】(3)求该钟表在1:15~1:30之间,时针与分针所在直线互相垂直的时刻。
[解题秘籍]
(1)根据分针每分钟转( 时针每分钟转 结合题意列关系式。
(2)令 列方程求解。
(3)根据(1)(2)中的方法求解。
强化训练47 某校门口道路中间的隔离护栏平面示意图如图所示,每根立柱宽为0.2米,立柱间距为3 米。
经测量发现立柱根数与护栏总长度(单位:米)之间的对应数据如下表(不完整):
立柱根数 1 2 3 4 5
护栏总长度/米 0.2 3.4 9.8
(1)将表格补充完整。
(2)设有x根立柱,护栏总长度为y米,则y与x 之间的关系式为 。
(3)求护栏总长度为93米时,立柱的根数。
秘题加练48 动点问题的函数图象
5.2 认识函数 打卡日期: 实际用时: 分钟
例48 如图1,在长方形ABCD中,E 是边AD 上一点,且AE=6 cm,点 P 从点B 出发,沿折线BE-ED-DC匀速运动,运动到点 C停止。已知点 P 的运动速度为2cm/s,运动时间为t(s),△BPC的面积为 y关于t 的函数图象如图2所示,给出下列结论:①a=7;②b=10;③BE=BC;④当t=3时,△PCD 为等腰三角形;⑤当t=10时,y=12。其中正确的是 (填序号)。
[解题秘籍]
先通过r=5,y=40 计算出 BC 的长,则DE的长即可求出,根据DE的长计算a 的值,b的值可以通过整个运动路程除以速度求得,当t=10 时,找到点 P 的位置,计算△BPC的面积即可得到y的值。
强化训练48
1.如图1,在△ABC中,动点 P 从点A 出发,沿折线AB→BC→CA匀速运动至点A 后停止。设点P 的运动路程为x,线段AP的长度为y,图2是y与x的函数关系的大致图象,其中F为曲线 DE的最低点,则△ABC的高线CG 的长为 。
2.如图,动点 P 从点B 出发,以每秒2cm 的速度在图1的边(相邻两边互相垂直)上按 B→C→D→E→F→A 的路线移动,相应的△ABP 的面积. 与点 P 的运动时间t(s)的图象如图2所示,已知AB=6 cm。
(1)a的值为 。
(2)当 时,求t 的值。
秘题加练49 函数的表达式
5.2 认识函数 打卡日期: 实际用时: 分钟
例49 棱长为a的小正方体,按照如图所示的方法摆放,自上而下分别叫第一层,第二层,…,第n层。若第n层的小正方体的个数记为S,解答下列问题:
(1)填写表格:
n 1 2 3 4
s 1 3
(2)观察上表可以发现S随n的变化而变化,请你写出S关于n的函数表达式。
…
[解题秘籍] 对于找规律类的题目,首先应找出哪些部分发生了变化,是按照什么规律变化的。通过分析找到各部分的变化规律后直接利用通式求解。
强化训练49 如图,自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm。
(1)观察图形填写下表:
链条节数/节 2 3 4
链条长度/cm
(2)如果x节链条的总长度是y,求y与x之间的关系式。
(3)如果一辆某种型号自行车的链条(安装前)由80节这样的链条组成,那么这根链条完成连接(安装到自行车上)后,它的周长是多少厘米
秘题加练50 用待定系数法求一次函数的表达式
5.3一次函数的意义 打卡日期: 实际用时: 分钟
例50 已知y是x的一次函数,当x=3时,y=1;当x=-2时,y=-4,,求这个一次函数的表达式。
[解题秘籍]
通过待定系数法求一次函数的表达式。
强化训练50
1.已知y是关于x 的一次函数,且当x=1时,y=-4;当x=2时,y=-6。
(1)求y关于x 的函数表达式。
(2)若-2
(1)y关于x的函数表达式。
(2)当.x=5时,y的值。
3.已知y是关于x 的一次函数,且当.x=3时,y=-2;当x=2时,y=-3。求:
(1)这个一次函数的表达式。
(2)当x=-3时,函数y的值。
(3)当y=2时,自变量x的值。
(4)当y>1时,自变量x的取值范围。
秘题加练51 数形结合——根据图象求一次函数的表达式
5.4一次函数的图象与性质 打卡日期: 实际用时: 分钟
例51 如图,在平面直角坐标系中,一次函数y=kx+5(k≠0)的图象 分别与x轴、y轴相交于A,B两点,正比例函数的图象 与l 相交于点C(2,4)。
(1)求k的值及直线l 的表达式。
(2)若 M是直线l 上一点,连结 OM,当 的面积是 的面积的2倍时,求点 M 的坐标。
[解题秘籍]
(1)直线 与 相交于点C,即点C既在 上,也在 上,利用待定系数法即可求解。
(2)将 和 中的OB边看作底,则点C和点M到OB 的距离,即点 C和点 M 的横坐标的绝对值即为高,再由两个三角形的面积关系求解。
强化训练51 如图,直线y=x+4分别交x轴、y轴于点A,B。直线 经过点B,交x轴于点C。
(1)求b的值和OA,OC的长。
(2)在 BC的延长线上取点 D,使DC=BC,过点 D 作 轴,交AB的延长线于点 E,记 的面积为 的面积为 求 的值。
秘题加练52 分类讨论———一次函数的区间最值问题
5.4一次函数的图象与性质
例52 若一次函数 y= kx+5(k≠0)在-1≤x≤4范围内有最大值17,求k的值。
[解题秘籍] 分两种情况:①若k<0,则当x=-1时,y有最大值17,代入表达式求解;②若k>0,则当x=4时,y有最大值17,代入表达式求解。
强化训练52 已知一次函数y= kx-k+2(k为常数,且k≠0)。
(1)若点(-1,3)在一次函数y= kx-k+2的图象上。
①求k的值。
②设 P=y+x,则当-2≤x≤5时,求 P 的最大值。
(2)若当m-3≤x≤m时,函数有最大值M,最小值 N,且M-N=6,求此时一次函数y的表达式。
秘题加练53 一次函数的应用(一)
5.5一次函数的简单应用 打卡日期: 实际用时: 分钟
例53 某地举办大型活动,该活动纪念品迅速成为热销商品。下表是某商店甲、乙两种活动纪念品的进价和售价:
商品价格 甲 乙
进价/(元/个) 40 100
售价/(元/个) 45 110
(1)该店第一次用3800元购进的甲、乙两种纪念品,售完后共获毛利润400元[毛利润=(售价一进价)×销售量]。该店第一次购进的甲、乙两种纪念品分别为多少个
(2)根据(1)中的销售情况,该店计划第二次进货时,在第一次进货量的基础上增加甲种纪念品的购进量,减少乙种纪念品的购进量,并且甲种纪念品增加的数量是乙种纪念品减少的数量的3倍。已知每种纪念品的进价、售价都不变,设毛利润为w元,乙种纪念品减少的数量为m个。
①求 w关于m 的函数表达式。
②若第二次进货的总资金不超过4000元,则全部销售后获得的最大毛利润是多少
[解题秘籍]
(1)设该店第一次购进的甲种纪念品有x个,乙种纪念品有y个,根据题意列出关于x,y的二元一次方程组。
(2)把题目中陈述的数量关系转化成数学式子即是函数表达式;通过总资金不超过4 000元,求出m 的取伤范围。再由函数的性质求出最值。
强化训练53 杨梅是某地重要的农业经济产品。请根据提供的材料解决问题。
探究杨梅的销售利润
材料一 某商贸公司经销甲、乙两个品种的杨梅,甲品种杨梅的进价为16元/斤,乙品种杨梅的进货总金额y(元)与进货量x(斤)在x≥10时满足的关系如图所示。经过试销,在H市销售甲、乙两个品种杨梅的售价分别定为20元/斤和25元/斤。
材料二 某日,该商贸公司收购了甲、乙两个品种的杨梅共1000斤,其中乙品种的收购量不低于200斤,且不高于500斤。
材料三 杨梅运到 H 市,商场发现顾客对甲、乙两个品种杨梅都很喜欢,于是决定把两种杨梅按同样的价格销售,并适当让利给消费者。
问题解决
任务一 (1)已知E(50,1100),F(100,2 100),求图中直线EF的函数表达式。
任务二 (2)若从收购点运到商场的其他各种费用还需要1800元,收购的杨梅能够全部卖完,设销售完甲、乙两个品种的杨梅所获总利润为w元(利润=销售额一进货金额一其他费用)。求总利润w(元)与乙品种杨梅的进货量x(斤)之间的函数关系式,并为该商贸公司设计出获得最大利润的收购方案。
任务三 (3)在任务二设计的收购方案的基础上,商场把任务二中的最大利润的 让利给消费者。若此时甲、乙两种杨梅的售价均定为每斤a元,求a的值(结果保留整数)。
秘题加练54 数形结合——一次函数与二元一次方程组
5.5一次函数的简单应用 打卡日期: 实际用时: 分钟
例54 如图,已知函数y=x+1和.y=ax+3(a≠0)的图象相交于点 P,点P 的横坐标为1。
(1)关于x,y的方程组 的解是 。
(2)a的值为 。
(3)求出函数y=x+1和y=ax+3的图象与x轴围成的几何图形的面积。
[解题秘籍]
由一次函数与二元一次方程组的联系知,方程组的解就是两个相应的一次函数图象的交点坐标的值。
强化训练54 【了解概念】已知函数 是自变量x的函数,当 时,称函数 为函数y 的“倍差函数”。在平面直角坐标系中,对于函数 y 图象上任意一点A(m,n),称点.B(m,2n-m)为点 A 关于函数. 的“倍差点”,则点 B 在函数y 的“倍差函数”的图象上。
【理解运用】例如:函数 当 时,称函数 是函数 的“倍差函数”。在平面直角坐标系中,函数 图象上任意一点A(m,n),点B(m,2n-m)为点A 关于函数 的“倍差点”,则点 B在函数 的“倍差函数 的图象上。
(1)求函数 的“倍差函数 的表达式。
(2)点 P(m,n)在函数. 的图象上,点P 关于函数 的“倍差点”为Q,若点 Q与点 P 的纵坐标的和为-2,求点 P 的坐标。
【拓展提升】(3)在(2)的条件下, 的“倍差函数”的图象交y轴于点 T,已知点A(t,t),B(t+1,t+2)。若直线AB与 有交点,求t的取值范围。
秘题加练55 一次函数的应用(二)
第5章 学习任务清单 打卡日期: 实际用时: 分钟
例55 小明和小丽相约周末一起去登山锻炼,沿着同一条路线,小丽先开始,并一直匀速登山。5分钟后,小明开始,小明中途休息了两次,每次休息后,登山速度增加5米/分,以便追上小丽,小丽的速度与小明的第一段速度相同。小明和小丽的登山信息如表所示,距离地面的高度y(米)与小丽的登山时间x(分)的函数关系如图所示。
时间 登山阶段 登山速度 登山高度
小丽 8:00至9:00 不分段 v 600米
小明 8:05至8:50 第一段 v 100米
第一次休息
第二段 v+5 200米
第二次休息
第三段 v+10 300米
(1)求小丽的登山速度v。
(2)求小明两次休息时间的总和。
(3)小明第二次休息后,在a 分钟时两人登山高度相等,求a 的值。
[解题秘籍]
(1)小丽的登山速度=小丽的登山路程÷小丽的登山时间。
(2)根据题中朗络的表格中的数据计算由除休息外小明登山的时间及小明竖山忌用时,即可得到小明固次休息时词的总和。
(3)两人登山高度相等,赌相等关系为:小丽昼山的速度×登山的时间a=300+小明第三段昼山的速度×(a一两次休息总用时一推迟出发的S分钟一登第一段山用时一整第二段山用时),把相关数值代入计算即可,
强化训练55 A,B两地相距290 千米,早上9:00,甲货车从 A 地出发匀速将一批物资运往B地,行驶一段路程后出现故障,即刻停车与B地联系。B地收到消息后立即派乙货车从B 地出发匀速去接运甲货车上的物资,乙货车遇到甲货车后,用了30分钟将物资从甲货车搬运到乙货车上,随后开往B地,两辆货车离开各自出发地的路程y(千米)与甲货车出发的时间x(时)的函数关系如图所示。
(1)直接写出甲货车、乙货车的速度。
(2)求乙货车在未遇到甲货车时,它离开出发地的路程y(千米)关于甲货车出发的时间x(时)的函数表达式。
(3)因实际需要,要求乙货车到达B地的时间比甲货车按原来的速度正常到达B 地的时间最多晚1个小时,问乙货车返回B地的速度至少为多少
秘题加练56 一次函数的综合
第5章 学习任务清单 打卡日期: 实际用时: 分钟
例56 如图,直线 y=x+4与x轴、y轴分别相交于点A,B,P 是射线BO上的动点(不与点 B重合),过点 B 作直线AP 的垂线,交x轴于点Q,垂足为C,连结OC。
(1)当点 P 在线段 BO 上时。
①求证:△AOP≌△BOQ。
②若 P 为BO 的中点,求△OCQ 的面积。
(2)在点 P 的运动过程中,是否存在某一位置,使得△OCQ是以OQ 为底的等腰三角形 若存在,求点 P 的坐标;若不存在,请说明理由。
[解题秘籍]
(1)由图象可得出OA=OB,由垂直关系可得出
(2)可求得直线AC和BQ 的表达式,进而求得点C 的坐标。
答案(3)当点 P 在线段OB 上时,可推出OC=BC=CQ,此时C是BQ 的中点,进而得出AQ=AB. 当点 P 在 BO的延长线上时,同理得出结果。
强化训练56 如图1,直线y=kx+1(k>0)分别与x轴,y轴相交于A,B两点,直线 分别与x轴,y轴相交于C,D两点,两条直线相交于点 E。
(1)点C的坐标为 ,点A 的坐标为 (点A 的坐标用含k 的代数式表示)。
(2)若点 A 关于 y轴的对称点.A'恰好落在 的内部,求k的取值范围。
(3)如图2,若D为CE 的中点,Q为直线AB 上一点,连结 DQ,记点 E关于直线DQ 的对称点为 请问:是否存在点Q,使得点E'恰好落在直线CD 上方的坐标轴上 若存在,请求出点 Q 的坐标;若不存在,请说明理由。
【强化训练47】 (1)6.6 13 (2)y=3.2x-3 (3)30
例48. ①③④
【强化训练48】
2.(1)24(2)7或12
例49.(1)6 10
【强化训练49】(1)4.2 5.9 7.6 (2)y=1.7x+0.8(3)136 cm
例50. y=x-2
【强化训练50】
1.(1)y=-2x-2 (2)-10
3.(1)y=x-5 (2)-8 (3)7 (4)x>6
例51.
(2)(4,3)或(-4,7)
【强化训练51】(1)b=4,OA=4,OC=3 (2)
例52. — 12或3
【强化训练52】(1)①- ②5(2)y=2x或y=-2x+4
例53.(1)甲种纪念品20个,乙种纪念品30个
(2)①w=5m+400(m>0且m为整数) ②450元
【强化训练53】 (1)y=20x+100
(2)w=x+2 100(200≤x≤500) (3)22
例54.(1)(t)y=2(2)-1 (3)4
【强化训练54】((1)y =x-4 (2)(2,0) (3)-4
【强化训练55】
(1)甲货车的速度是60千米/时,乙货车的速度是100 千米/时
(2)y=100x-150(1.5≤x≤3.5) 千米/时
例56.(1)①略②
(2)存在。点 P 的坐标为(0,4 -4)或(
【强化训练56】(1)(4,0) (- ,0) (2)k>
(3)存在。点Q的坐标为 或
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
