2.4等腰三角形的判定定理 同步练习(含答案)
文档属性
| 名称 | 2.4等腰三角形的判定定理 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 476.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 19:34:52 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2.4 等腰三角形的判定定理
一、单选题
1.如图,,的平分线相交于D,过点D作,交于E,交于F,那么下列结论中:①;②;③;④的周长,其中正确的有几个( )
A.1个 B.2个 C.3个 D.4个
2.如图在正方形网格中,等于( )
A. B. C. D.
3.如图,在中,,,E为边的中点,交延长线于点D,平分交于点F,连接.下面结论不一定成立的是( )
A. B. C. D.
4.下列说法中,正确的有( )
A.两个全等的三角形一定关于某直线对称
B.等腰三角形的高、中线、角平分线互相重合
C.等腰三角形是轴对称图形,对称轴为等腰三角形的高
D.若三角形一个外角的平分线平行于三角形的一边,则这个三角形为等腰三角形
5.下列说法错误的是( )
A.有两边相等的三角形是等腰三角形
B.直角三角形不可能是等腰三角形
C.有两个角为60°的三角形是等边三角形
D.有一个角为60°的等腰三角形是等边三角形
二、填空题
6.已知点在反比例函数的图象上,点在轴正半轴上,若为等腰直角三角形,则的长为 .
7.如图,若,则的度数为 .
8.已知等腰三角形的一边长为,一个内角为,则它的周长是 ;
9.在中,,,,则的周长为 .
10.如图,已知∠ABC=∠ADE=90°,AB=BC,AD=DE,其中点D是边BC所在射线上一动点(点D不与B,C重合),连接AC,EC,则∠DCE的度数为 .
11.由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小颖同学设计一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图①,衣架杆(O为衣架的固定点):如图②,若衣架收拢时,,则此时A,B两点之间的距离是 cm
三、计算题
12.已知,,是的三边长.
(1)若,,满足,试判断的形状;
(2)化简:
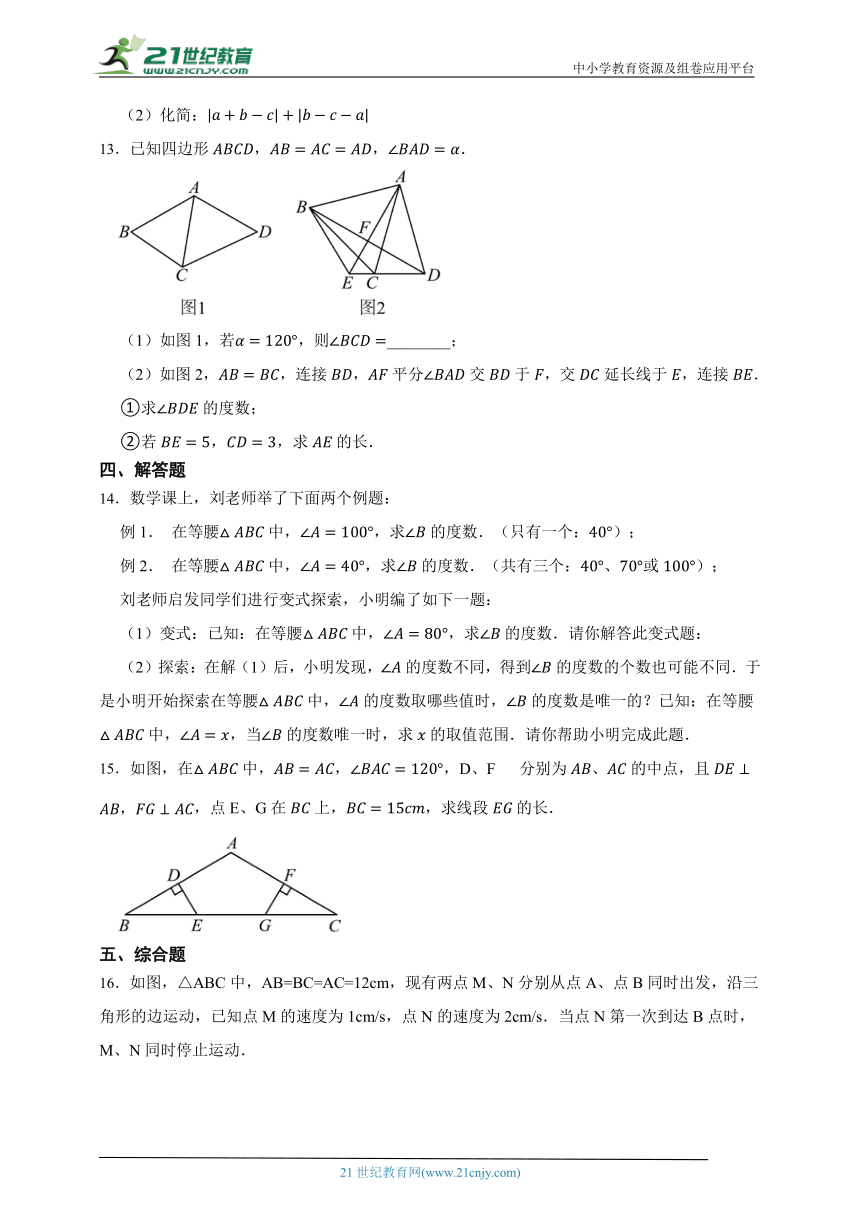
13.已知四边形,,.
(1)如图1,若,则________;
(2)如图2,,连接,平分交于,交延长线于,连接.
①求的度数;
②若,,求的长.
四、解答题
14.数学课上,刘老师举了下面两个例题:
例1. 在等腰中,,求的度数.(只有一个:);
例2. 在等腰中,,求的度数.(共有三个:、或);
刘老师启发同学们进行变式探索,小明编了如下一题:
(1)变式:已知:在等腰中,,求的度数.请你解答此变式题:
(2)探索:在解(1)后,小明发现,的度数不同,得到的度数的个数也可能不同.于是小明开始探索在等腰中,的度数取哪些值时,的度数是唯一的?已知:在等腰中,,当的度数唯一时,求的取值范围.请你帮助小明完成此题.
15.如图,在中,,,D、F 分别为、的中点,且,点E、G在上,,求线段的长.
五、综合题
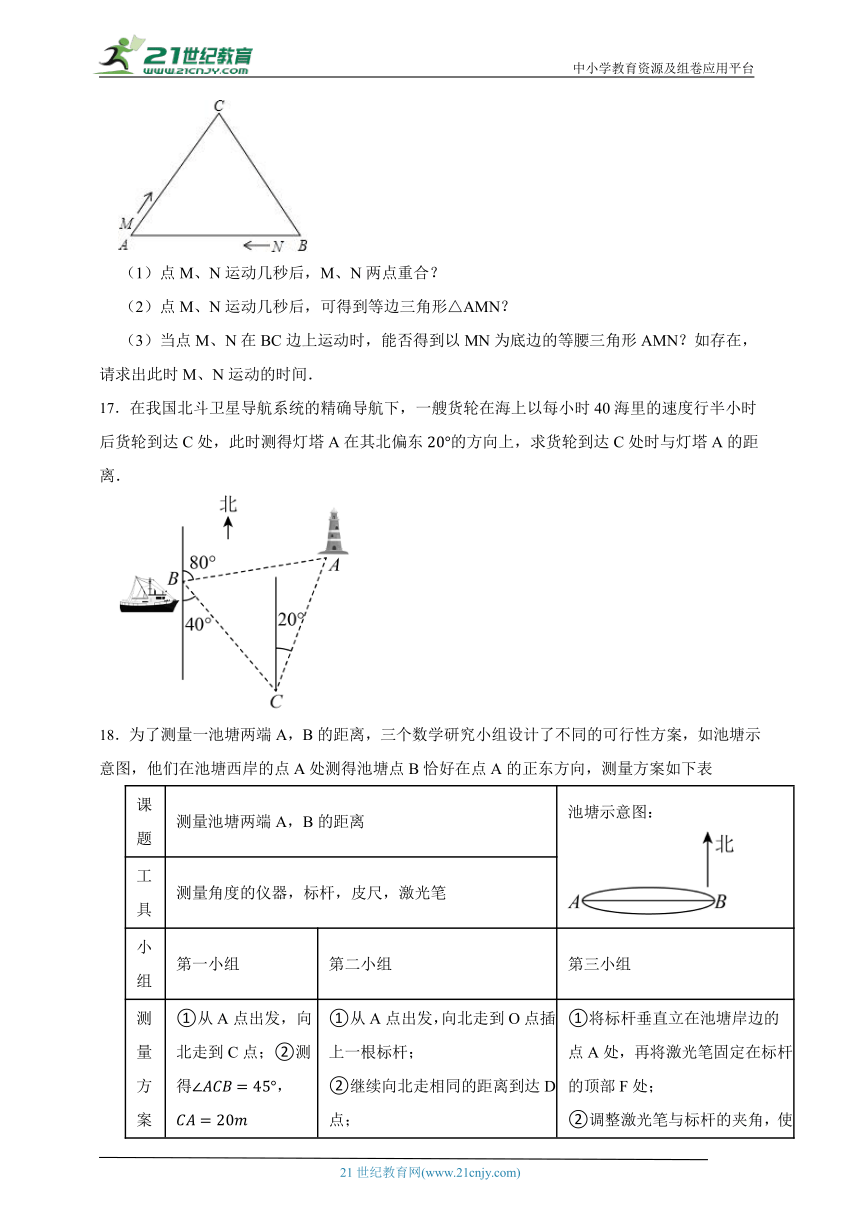
16.如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.
(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.
17.在我国北斗卫星导航系统的精确导航下,一艘货轮在海上以每小时40海里的速度行半小时后货轮到达C处,此时测得灯塔A在其北偏东的方向上,求货轮到达C处时与灯塔A的距离.
18.为了测量一池塘两端A,B的距离,三个数学研究小组设计了不同的可行性方案,如池塘示意图,他们在池塘西岸的点A处测得池塘点B恰好在点A的正东方向,测量方案如下表
课题 测量池塘两端A,B的距离 池塘示意图:
工具 测量角度的仪器,标杆,皮尺,激光笔
小组 第一小组 第二小组 第三小组
测量方案 ①从A点出发,向北走到C点;②测得, ①从A点出发,向北走到O点插上一根标杆; ②继续向北走相同的距离到达D点; ③再向西走到E点,使B,O,E三点共线; ④测得 ①将标杆垂直立在池塘岸边的点A处,再将激光笔固定在标杆的顶部F处; ②调整激光笔与标杆的夹角,使其射出的光线正好落在池塘对岸的点B; ③保持标杆与激光笔的夹角不变,转动标杆,使激光笔射出的光线落在同岸的点G,此时; ④测得:数据1:; 数据2:.
测量示意图
(1)第一小组测得即的距离,证明方法如下:
证明: (转右框) (理由:______)
(2)请用第二小组的方案,求出池塘两端A,B的距离;
(3)其他小组的同学发现,第三小组方案的第④步只用其中一个数据就可以求出池塘两端A,B的距离,请你在第④步中选择一个有效数据求出池塘两端A,B的距离.
答案解析部分
1.【答案】B
【知识点】三角形内角和定理;等腰三角形的判定与性质;内错角的概念
2.【答案】C
【知识点】等腰三角形的判定与性质;三角形全等的判定-SAS
3.【答案】D
【知识点】等腰三角形的判定与性质;三角形全等的判定-SAS
4.【答案】D
【知识点】等腰三角形的判定与性质;轴对称的性质
5.【答案】B
【知识点】等腰三角形的判定;等边三角形的判定
6.【答案】或
【知识点】等腰三角形的判定与性质
7.【答案】
【知识点】三角形外角的概念及性质;等腰三角形的性质;等边三角形的判定与性质
8.【答案】
【知识点】等边三角形的判定与性质
9.【答案】9
【知识点】等边三角形的判定与性质
10.【答案】135°或45°
【知识点】余角、补角及其性质;等腰三角形的判定与性质
11.【答案】16
【知识点】等边三角形的判定与性质
12.【答案】(1)是等边三角形
(2)
【知识点】三角形三边关系;等边三角形的判定;绝对值的非负性;化简含绝对值有理数
13.【答案】(1)
(2)①;②
【知识点】等腰三角形的判定与性质
14.【答案】(1)
(2)或
【知识点】三角形内角和定理;等腰三角形的性质;等边三角形的判定与性质
15.【答案】
【知识点】三角形内角和定理;线段垂直平分线的性质;等腰三角形的性质;等边三角形的判定与性质
16.【答案】(1)解:设点M、N运动x秒后,M、N两点重合,
x×1+12=2x,
解得:x=12
(2)解:设点M、N运动t秒后,可得到等边三角形△AMN,如图①,
AM=t×1=t,AN=AB﹣BN=12﹣2t,
∵三角形△AMN是等边三角形,
∴t=12﹣2t,
解得t=4,
∴点M、N运动4秒后,可得到等边三角形△AMN
(3)解:当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,
由(1)知12秒时M、N两点重合,恰好在C处,
如图②,假设△AMN是等腰三角形,
∴AN=AM,
∴∠AMN=∠ANM,
∴∠AMC=∠ANB,
∵AB=BC=AC,
∴△ACB是等边三角形,
∴∠C=∠B,
在△ACM和△ABN中,
∵ ,
∴△ACM≌△ABN,
∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,
∴CM=y﹣12,NB=36﹣2y,CM=NB,
y﹣12=36﹣2y,
解得:y=16.故假设成立.
∴当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形AMN,此时M、N运动的时间为16秒.
【知识点】等腰三角形的性质;等边三角形的判定与性质
17.【答案】货轮到达处时与灯塔的距离是20海里.
【知识点】等边三角形的判定与性质
18.【答案】(1)等角对等边
(2)A,B的距离为
(3)选择有效数据:,A,B的距离为
【知识点】等腰三角形的判定
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.4 等腰三角形的判定定理
一、单选题
1.如图,,的平分线相交于D,过点D作,交于E,交于F,那么下列结论中:①;②;③;④的周长,其中正确的有几个( )
A.1个 B.2个 C.3个 D.4个
2.如图在正方形网格中,等于( )
A. B. C. D.
3.如图,在中,,,E为边的中点,交延长线于点D,平分交于点F,连接.下面结论不一定成立的是( )
A. B. C. D.
4.下列说法中,正确的有( )
A.两个全等的三角形一定关于某直线对称
B.等腰三角形的高、中线、角平分线互相重合
C.等腰三角形是轴对称图形,对称轴为等腰三角形的高
D.若三角形一个外角的平分线平行于三角形的一边,则这个三角形为等腰三角形
5.下列说法错误的是( )
A.有两边相等的三角形是等腰三角形
B.直角三角形不可能是等腰三角形
C.有两个角为60°的三角形是等边三角形
D.有一个角为60°的等腰三角形是等边三角形
二、填空题
6.已知点在反比例函数的图象上,点在轴正半轴上,若为等腰直角三角形,则的长为 .
7.如图,若,则的度数为 .
8.已知等腰三角形的一边长为,一个内角为,则它的周长是 ;
9.在中,,,,则的周长为 .
10.如图,已知∠ABC=∠ADE=90°,AB=BC,AD=DE,其中点D是边BC所在射线上一动点(点D不与B,C重合),连接AC,EC,则∠DCE的度数为 .
11.由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小颖同学设计一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图①,衣架杆(O为衣架的固定点):如图②,若衣架收拢时,,则此时A,B两点之间的距离是 cm
三、计算题
12.已知,,是的三边长.
(1)若,,满足,试判断的形状;
(2)化简:
13.已知四边形,,.
(1)如图1,若,则________;
(2)如图2,,连接,平分交于,交延长线于,连接.
①求的度数;
②若,,求的长.
四、解答题
14.数学课上,刘老师举了下面两个例题:
例1. 在等腰中,,求的度数.(只有一个:);
例2. 在等腰中,,求的度数.(共有三个:、或);
刘老师启发同学们进行变式探索,小明编了如下一题:
(1)变式:已知:在等腰中,,求的度数.请你解答此变式题:
(2)探索:在解(1)后,小明发现,的度数不同,得到的度数的个数也可能不同.于是小明开始探索在等腰中,的度数取哪些值时,的度数是唯一的?已知:在等腰中,,当的度数唯一时,求的取值范围.请你帮助小明完成此题.
15.如图,在中,,,D、F 分别为、的中点,且,点E、G在上,,求线段的长.
五、综合题
16.如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.
(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.
17.在我国北斗卫星导航系统的精确导航下,一艘货轮在海上以每小时40海里的速度行半小时后货轮到达C处,此时测得灯塔A在其北偏东的方向上,求货轮到达C处时与灯塔A的距离.
18.为了测量一池塘两端A,B的距离,三个数学研究小组设计了不同的可行性方案,如池塘示意图,他们在池塘西岸的点A处测得池塘点B恰好在点A的正东方向,测量方案如下表
课题 测量池塘两端A,B的距离 池塘示意图:
工具 测量角度的仪器,标杆,皮尺,激光笔
小组 第一小组 第二小组 第三小组
测量方案 ①从A点出发,向北走到C点;②测得, ①从A点出发,向北走到O点插上一根标杆; ②继续向北走相同的距离到达D点; ③再向西走到E点,使B,O,E三点共线; ④测得 ①将标杆垂直立在池塘岸边的点A处,再将激光笔固定在标杆的顶部F处; ②调整激光笔与标杆的夹角,使其射出的光线正好落在池塘对岸的点B; ③保持标杆与激光笔的夹角不变,转动标杆,使激光笔射出的光线落在同岸的点G,此时; ④测得:数据1:; 数据2:.
测量示意图
(1)第一小组测得即的距离,证明方法如下:
证明: (转右框) (理由:______)
(2)请用第二小组的方案,求出池塘两端A,B的距离;
(3)其他小组的同学发现,第三小组方案的第④步只用其中一个数据就可以求出池塘两端A,B的距离,请你在第④步中选择一个有效数据求出池塘两端A,B的距离.
答案解析部分
1.【答案】B
【知识点】三角形内角和定理;等腰三角形的判定与性质;内错角的概念
2.【答案】C
【知识点】等腰三角形的判定与性质;三角形全等的判定-SAS
3.【答案】D
【知识点】等腰三角形的判定与性质;三角形全等的判定-SAS
4.【答案】D
【知识点】等腰三角形的判定与性质;轴对称的性质
5.【答案】B
【知识点】等腰三角形的判定;等边三角形的判定
6.【答案】或
【知识点】等腰三角形的判定与性质
7.【答案】
【知识点】三角形外角的概念及性质;等腰三角形的性质;等边三角形的判定与性质
8.【答案】
【知识点】等边三角形的判定与性质
9.【答案】9
【知识点】等边三角形的判定与性质
10.【答案】135°或45°
【知识点】余角、补角及其性质;等腰三角形的判定与性质
11.【答案】16
【知识点】等边三角形的判定与性质
12.【答案】(1)是等边三角形
(2)
【知识点】三角形三边关系;等边三角形的判定;绝对值的非负性;化简含绝对值有理数
13.【答案】(1)
(2)①;②
【知识点】等腰三角形的判定与性质
14.【答案】(1)
(2)或
【知识点】三角形内角和定理;等腰三角形的性质;等边三角形的判定与性质
15.【答案】
【知识点】三角形内角和定理;线段垂直平分线的性质;等腰三角形的性质;等边三角形的判定与性质
16.【答案】(1)解:设点M、N运动x秒后,M、N两点重合,
x×1+12=2x,
解得:x=12
(2)解:设点M、N运动t秒后,可得到等边三角形△AMN,如图①,
AM=t×1=t,AN=AB﹣BN=12﹣2t,
∵三角形△AMN是等边三角形,
∴t=12﹣2t,
解得t=4,
∴点M、N运动4秒后,可得到等边三角形△AMN
(3)解:当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,
由(1)知12秒时M、N两点重合,恰好在C处,
如图②,假设△AMN是等腰三角形,
∴AN=AM,
∴∠AMN=∠ANM,
∴∠AMC=∠ANB,
∵AB=BC=AC,
∴△ACB是等边三角形,
∴∠C=∠B,
在△ACM和△ABN中,
∵ ,
∴△ACM≌△ABN,
∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,
∴CM=y﹣12,NB=36﹣2y,CM=NB,
y﹣12=36﹣2y,
解得:y=16.故假设成立.
∴当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形AMN,此时M、N运动的时间为16秒.
【知识点】等腰三角形的性质;等边三角形的判定与性质
17.【答案】货轮到达处时与灯塔的距离是20海里.
【知识点】等边三角形的判定与性质
18.【答案】(1)等角对等边
(2)A,B的距离为
(3)选择有效数据:,A,B的距离为
【知识点】等腰三角形的判定
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
