2.7探索勾股定理 同步练习(含答案)
文档属性
| 名称 | 2.7探索勾股定理 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 522.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 19:39:28 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2.7 探索勾股定理
一、单选题
1.如图,在中,,,.将折叠,使点A与的中点D重合,则的长是( )
A.4 B.3 C.6 D.5
2.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长.在这个问题中,AC的长为( )
A.4尺 B.尺 C.尺 D.5尺
3.下列数组中,能构成勾股数的是( )
A.1,1, B.0.3,0.4,0.5
C.5,12,13 D.,,
4.若直角三角形的两边长分别是5和12,则它的斜边长是( )
A.13 B.13或 C. D.12或13
5.如图,中,,把沿直线向右平移3个单位长度得到,则四边形的面积是( )
A.22 B.18 C.15 D.24
二、填空题
6.如图,线段 、 ,那么线段 的长度为 .
7.如图,在中,,,是的中线,是的中点,连接,,若,垂足为,则的结果为 .
8.如图,有两棵树,一颗高10米,另一棵高3米,两树相距24米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行 米.
9.在中,若其三条边的长度分别为9、12、15,则这样的三角形的面积是
10.如图,已知线段,分别以点A,B为圆心,大于长为半径画弧,两弧相交于点E,F,作直线交于点D,在直线上取一点C使,连接、,点G为的中点,连接,则的周长是 .
11.如图,小正方形边长为1,连接小正方形的三个顶点,可得,则边上的高是 .
三、计算题
12.从旗杆的顶端系一条绳子,垂到地面还多米,小敏拉起绳子下端绷紧,刚好接触地面,发现绳子下端距离旗杆底部米,小敏马上计算出旗杆的高度,你知道她是如何解的吗?
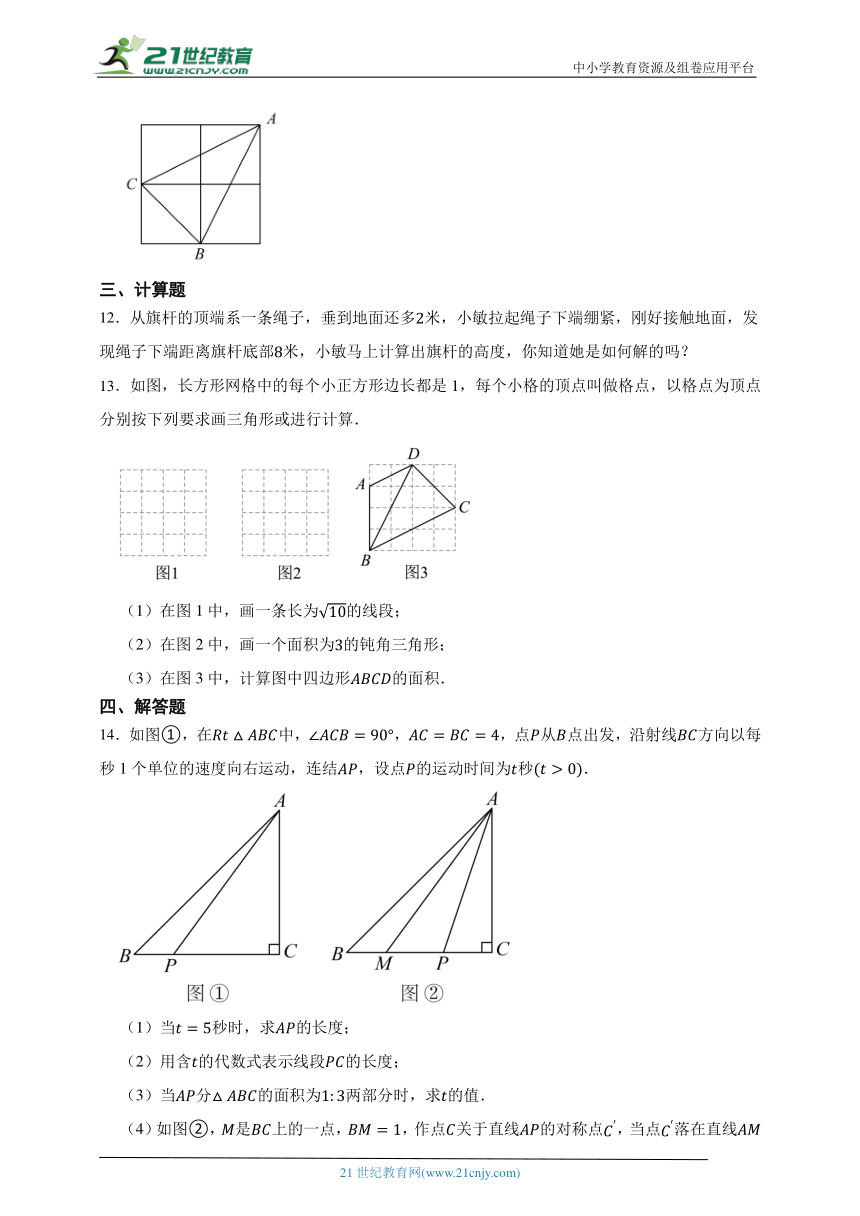
13.如图,长方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形或进行计算.
(1)在图1中,画一条长为的线段;
(2)在图2中,画一个面积为的钝角三角形;
(3)在图3中,计算图中四边形的面积.
四、解答题
14.如图①,在中,,,点从点出发,沿射线方向以每秒1个单位的速度向右运动,连结,设点的运动时间为秒.
(1)当秒时,求的长度;
(2)用含的代数式表示线段的长度;
(3)当分的面积为两部分时,求的值.
(4)如图②,是上的一点,,作点关于直线的对称点,当点落在直线上时,直接写出的值.
15.如图,已知在中,,有一动点P在折线段上运动,速度为2个单位,运动时间t.
(1)当 时,;
(2)若平分,求运动时间t;
(3)当t为何值时,为轴对称图形.
五、综合题
16.阅读并解答问题:
明朝数学家程大位在数学著作《直指算法统宗》中以《西江月》词牌叙述了一道“荡秋千”问题:
原文:平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记,仕女佳人争蹴,终朝笑语欢嬉,良工高士素好奇,算出索有几?
译文:如图,有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,试问绳索有多长?(注古代5尺为1步)
建立数学模型,解决问题:
如图,秋千绳索静止的时候,踏板离地高一尺(尺),将它往前推进两步(尺),此时踏板升高离地五尺(尺),已知于点C,于点D,于点E,,求秋千绳索(或)的长度.
17.一辆轿车从地以的速度向正东方向行驶,同时一辆货车以速度从地向正北方向行驶,2小时后两车同时到达走向公路上的两地.
(1)求两地的距离;
(2)若要从地修建一条最短新路到达公路,求的距离.
18.已知某开发区有一块四边形的空地,如图所示,现计划在空地上种植草皮,经测量,,,,,若每平方米草皮需要200元,问要多少投入?
六、实践探究题
19.阅读材料,解答下面问题:我们新定义一种三角形,两边的平方和等于第三边平方2倍的三角形叫做奇异三角形.
(1)理解并填空:
①根据奇异三角形的定义,请你判断:等边三角形一定 (填“是”或“不是”)奇异三角形;
②若某三角形的三边长分别为1,,2,则该三角形 (填“是”或“不是”)奇异三角形;
(2)探究:在中,两边长分别是a,c,且,,则这个三角形是否是奇异三角形?请说明理由.
答案解析部分
1.【答案】A
【知识点】勾股定理
2.【答案】C
【知识点】勾股定理
3.【答案】C
【知识点】勾股数
4.【答案】D
【知识点】勾股定理
5.【答案】C
【知识点】勾股定理;平移的性质
6.【答案】
【知识点】勾股定理
7.【答案】
【知识点】勾股定理;直角三角形斜边上的中线
8.【答案】25
【知识点】勾股定理的应用
9.【答案】54
【知识点】勾股定理的逆定理
10.【答案】
【知识点】线段垂直平分线的性质;勾股定理;尺规作图-垂直平分线;直角三角形斜边上的中线
11.【答案】
【知识点】三角形的角平分线、中线和高;勾股定理
12.【答案】米.
【知识点】勾股定理;勾股定理的实际应用-旗杆高度问题
13.【答案】(1)图解析;
(2)图解析;
(3)
【知识点】勾股定理
14.【答案】(1)
(2)当时,;当时,
(3)秒或秒
(4)秒或秒
【知识点】勾股定理;一元一次方程的实际应用-几何问题
15.【答案】(1)2
(2)
(3)或或或
【知识点】角平分线的性质;勾股定理;等腰三角形的概念
16.【答案】14.5尺
【知识点】一元一次方程的实际应用-几何问题;勾股定理的实际应用-旗杆高度问题
17.【答案】(1);
(2).
【知识点】垂线段最短及其应用;勾股定理的实际应用-(行驶、航行)方向问题
18.【答案】需要投入元
【知识点】勾股定理;勾股定理的逆定理
19.【答案】(1)①是,②是
(2)解:当c为斜边时,则,
由于,
故不是奇异三角形;
当b为斜边时,,
则有,
所以是奇异三角形.
答:当c为斜边时,不是奇异三角形;当b为斜边时,是奇异三角形.
【知识点】等边三角形的性质;勾股定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.7 探索勾股定理
一、单选题
1.如图,在中,,,.将折叠,使点A与的中点D重合,则的长是( )
A.4 B.3 C.6 D.5
2.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长.在这个问题中,AC的长为( )
A.4尺 B.尺 C.尺 D.5尺
3.下列数组中,能构成勾股数的是( )
A.1,1, B.0.3,0.4,0.5
C.5,12,13 D.,,
4.若直角三角形的两边长分别是5和12,则它的斜边长是( )
A.13 B.13或 C. D.12或13
5.如图,中,,把沿直线向右平移3个单位长度得到,则四边形的面积是( )
A.22 B.18 C.15 D.24
二、填空题
6.如图,线段 、 ,那么线段 的长度为 .
7.如图,在中,,,是的中线,是的中点,连接,,若,垂足为,则的结果为 .
8.如图,有两棵树,一颗高10米,另一棵高3米,两树相距24米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行 米.
9.在中,若其三条边的长度分别为9、12、15,则这样的三角形的面积是
10.如图,已知线段,分别以点A,B为圆心,大于长为半径画弧,两弧相交于点E,F,作直线交于点D,在直线上取一点C使,连接、,点G为的中点,连接,则的周长是 .
11.如图,小正方形边长为1,连接小正方形的三个顶点,可得,则边上的高是 .
三、计算题
12.从旗杆的顶端系一条绳子,垂到地面还多米,小敏拉起绳子下端绷紧,刚好接触地面,发现绳子下端距离旗杆底部米,小敏马上计算出旗杆的高度,你知道她是如何解的吗?
13.如图,长方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形或进行计算.
(1)在图1中,画一条长为的线段;
(2)在图2中,画一个面积为的钝角三角形;
(3)在图3中,计算图中四边形的面积.
四、解答题
14.如图①,在中,,,点从点出发,沿射线方向以每秒1个单位的速度向右运动,连结,设点的运动时间为秒.
(1)当秒时,求的长度;
(2)用含的代数式表示线段的长度;
(3)当分的面积为两部分时,求的值.
(4)如图②,是上的一点,,作点关于直线的对称点,当点落在直线上时,直接写出的值.
15.如图,已知在中,,有一动点P在折线段上运动,速度为2个单位,运动时间t.
(1)当 时,;
(2)若平分,求运动时间t;
(3)当t为何值时,为轴对称图形.
五、综合题
16.阅读并解答问题:
明朝数学家程大位在数学著作《直指算法统宗》中以《西江月》词牌叙述了一道“荡秋千”问题:
原文:平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记,仕女佳人争蹴,终朝笑语欢嬉,良工高士素好奇,算出索有几?
译文:如图,有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,试问绳索有多长?(注古代5尺为1步)
建立数学模型,解决问题:
如图,秋千绳索静止的时候,踏板离地高一尺(尺),将它往前推进两步(尺),此时踏板升高离地五尺(尺),已知于点C,于点D,于点E,,求秋千绳索(或)的长度.
17.一辆轿车从地以的速度向正东方向行驶,同时一辆货车以速度从地向正北方向行驶,2小时后两车同时到达走向公路上的两地.
(1)求两地的距离;
(2)若要从地修建一条最短新路到达公路,求的距离.
18.已知某开发区有一块四边形的空地,如图所示,现计划在空地上种植草皮,经测量,,,,,若每平方米草皮需要200元,问要多少投入?
六、实践探究题
19.阅读材料,解答下面问题:我们新定义一种三角形,两边的平方和等于第三边平方2倍的三角形叫做奇异三角形.
(1)理解并填空:
①根据奇异三角形的定义,请你判断:等边三角形一定 (填“是”或“不是”)奇异三角形;
②若某三角形的三边长分别为1,,2,则该三角形 (填“是”或“不是”)奇异三角形;
(2)探究:在中,两边长分别是a,c,且,,则这个三角形是否是奇异三角形?请说明理由.
答案解析部分
1.【答案】A
【知识点】勾股定理
2.【答案】C
【知识点】勾股定理
3.【答案】C
【知识点】勾股数
4.【答案】D
【知识点】勾股定理
5.【答案】C
【知识点】勾股定理;平移的性质
6.【答案】
【知识点】勾股定理
7.【答案】
【知识点】勾股定理;直角三角形斜边上的中线
8.【答案】25
【知识点】勾股定理的应用
9.【答案】54
【知识点】勾股定理的逆定理
10.【答案】
【知识点】线段垂直平分线的性质;勾股定理;尺规作图-垂直平分线;直角三角形斜边上的中线
11.【答案】
【知识点】三角形的角平分线、中线和高;勾股定理
12.【答案】米.
【知识点】勾股定理;勾股定理的实际应用-旗杆高度问题
13.【答案】(1)图解析;
(2)图解析;
(3)
【知识点】勾股定理
14.【答案】(1)
(2)当时,;当时,
(3)秒或秒
(4)秒或秒
【知识点】勾股定理;一元一次方程的实际应用-几何问题
15.【答案】(1)2
(2)
(3)或或或
【知识点】角平分线的性质;勾股定理;等腰三角形的概念
16.【答案】14.5尺
【知识点】一元一次方程的实际应用-几何问题;勾股定理的实际应用-旗杆高度问题
17.【答案】(1);
(2).
【知识点】垂线段最短及其应用;勾股定理的实际应用-(行驶、航行)方向问题
18.【答案】需要投入元
【知识点】勾股定理;勾股定理的逆定理
19.【答案】(1)①是,②是
(2)解:当c为斜边时,则,
由于,
故不是奇异三角形;
当b为斜边时,,
则有,
所以是奇异三角形.
答:当c为斜边时,不是奇异三角形;当b为斜边时,是奇异三角形.
【知识点】等边三角形的性质;勾股定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
