5.1常量与变量 同步练习(含答案)
文档属性
| 名称 | 5.1常量与变量 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 533.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 19:44:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
5.1 常量与变量
一、单选题
1.某校八年级(4)班用150元购买了某品牌乒乓球个,该品牌乒乓球的单价是元/个,其函数关系式为,在这个问题中,变量是( )
A.150,x B.150,y C.x,y D.,
2.在利用太阳能热水器来加热水的过程中,热水器里的水温会随着太阳照射时间的长短而变化,在这个变化过程中,自变量是( )
A.热水器里的水温 B.太阳光的强弱
C.热水器的容积 D.太阳照射时间的长短
3.甲、乙两地相距50千米,若一辆汽车以50千米/时的速度从甲地到乙地,则汽车距乙地的路程s(千米)与行驶的时间t(时)之间的关系式s=50-50t中,常量的个数为( )
A.1 B.2 C.3 D.4
4.对于圆的周长公式,下列说法正确的是( )
A.C是变量,是常量 B.C是常量,是变量
C.C是变量,是常量 D.C是变量,是常量
5.如图是加油机上的数据显示牌,其中的变量是( )
A.金额 B.单价 C.油量 D.金额和油量
二、填空题
6.某人购进一批苹果,到市场零售,已知卖出苹果数量千克与售价元的关系如下表:
数量千克 2 3 4 5
售价元
用x表示y的关系式可表示为 .
7.某公司制作毕业纪念册的收费标准是:每册收取材料费4元,则总收费y(元)与制作纪念册的册数x (册)之间的关系式为 .
8.某汽车生产厂对其生产的型汽车进行油耗试验(油箱已加满),试验中汽车为匀速行驶,在行驶过程中,油箱的余油量(升)与行驶时间(小时)之间的关系如下表:
(小时) 0 1 2 3
(升) 80 72 64 56
则与之间的关系式为 .
9.我国首辆火星车正式被命名为“祝融”,为应对极限温度环境,火星车使用的是新型隔温材料——纳米气凝胶,该材料导热率与温度的关系如表:
温度 100 150 200 250 300 350 400
导热率
根据表格中两者的对应关系,若导热率为,则温度为 .
10.某水果店卖出的苹果数量(千克)与售价(元)之间的关系如下表:
苹果数量x(千克) 0.5 1 1.5 2 2.5 3 3.5 …
售价y(元) 2.5 5 7.5 10 12.5 15 17.5 …
上表反映了两个变量之间的关系,则与的关系式为
11.将一根长为的铁丝制作成一个长方形,则这个长方形的长y()与宽x()之间的关系式为 .(不用写出自变量x的取值范围)
三、计算题
12.探索计算:弹簧挂上物体后会伸长.已知一弹簧的长度()与所挂物体的质量()之间的关系如下表:
所挂物体的质量/
弹簧的长度/
(1)当所挂物体的质量为时,弹簧的长度是_______________________;
(2)在弹性限度内如果所挂物体的质量为,弹簧的长度为,根据上表直接写出与的关系式_____________;
(3)当所挂物体的质量为时,请求出弹簧的长度;
(4)如果弹簧的最大长度为,那么该弹簧最多能挂质量为多少的物体?
13.果实成熟从树上落到地面,它下落的高度与经过的时间有如下的关系:
时间t/秒 0.5 0.6 0.7 0.8 0.9 …
高度h/米 …
(1)上表反映了哪两个变量之间的关系?其中自变量是什么?因变量是什么?
(2)请你按照表中呈现的规律,列出果子下落的高度(米)与时间(秒)之间的关系式;
(3)现有一颗果子经过2秒后离地面一米,请计算这颗果子开始下落时离地面的高度是多少米?
四、解答题
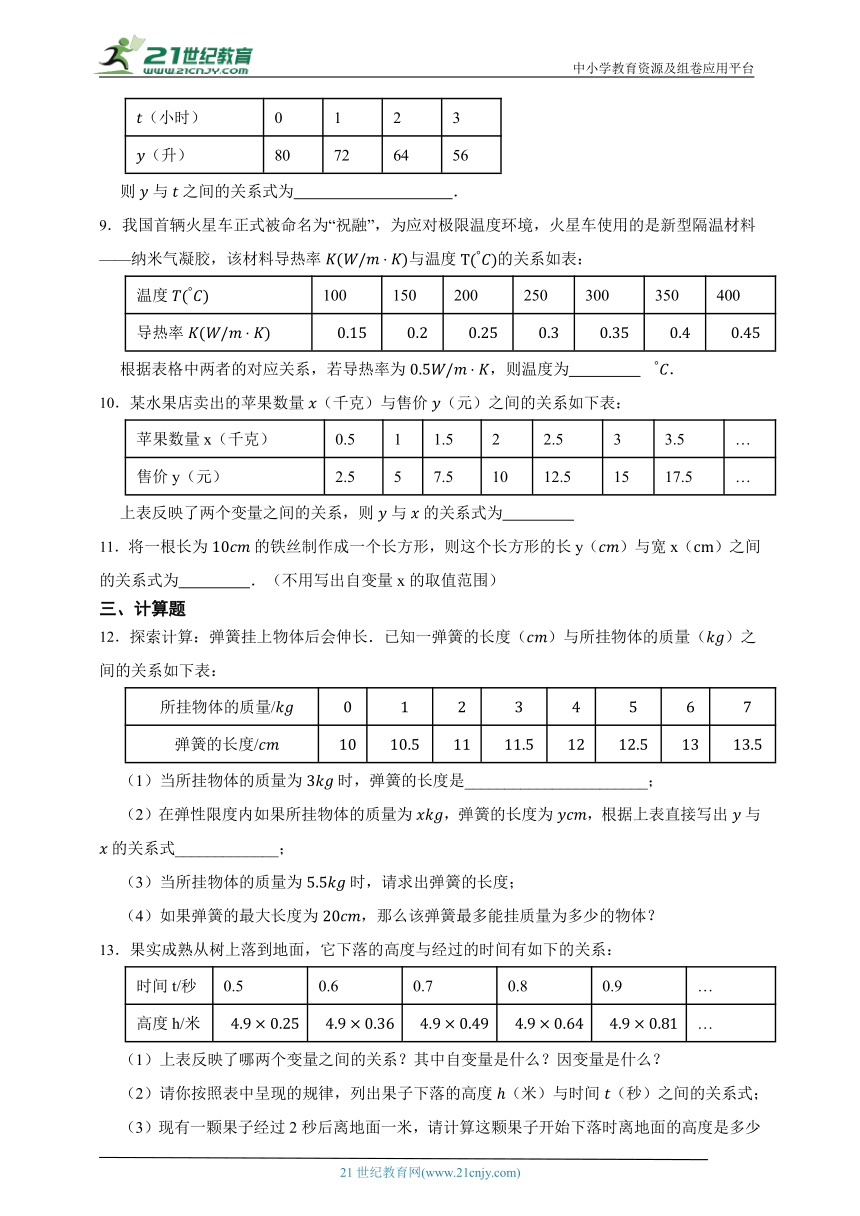
14.全球首次“人机共跑”半程马拉松于年月日在北京完赛,经过时分秒的奔跑,机器人“天工”率先冲过终点拱门,夺得桂冠.受到该项赛事启发,某中学机器人兴趣小组也举办了“机器人竞速比赛”,比赛中甲、乙两台机器人的赛跑路程和赛跑时间之间的关系如图所示,请根据图象信息回答下列问题:
(1)本次比赛全程是___________,机器人___________先到达终点;
(2)机器人甲的平均速度是___________,其路程和时间的关系式是___________;
(3)机器人乙由于故障在途中停留了___________,恢复运行后,机器人乙的速度___________机器人甲的速度.(填“”“”或“”)
15.一个蓄水池有水,打开放水闸门放水,水池里的水和放水时间的关系如表,回答下面问题:
放水时间(分钟) 1 2 3 4 5 …
水池中水量 48 46 42 40 …
(1)如图所示,将表格补充完整; .
(2)根据表格中的数据,说明在放完水前,水池中水量是随放水时间的增长而怎样变化的?
(3)当放水时间为7分钟时,水池中水量是多少立方米?
五、综合题
16.王老师打一篇演讲稿,每分钟打字的个数与所需时间之间的关系如下表:
每分钟打字的个数(个) 120 100 75 60
所需时间(分) 25 30 40 50
(1)这篇演讲稿共有多少字?
(2)所需时间是怎样随着每分钟打字的个数的变化而变化?
(3)用表示所需时间,用表示每分钟打字的个数,用式子表示与的关系.与成什么比例关系?当时,求的值.
17.
(1)地表以下的岩层的温度和它所处的深度有以下关系:
①上表反映了两个变量之间的关系,哪个是自变量?哪个是因变量?
②深度每增加 ,温度增加多少摄氏度?
③估计 深处的岩层温度是多少摄氏度.
(2)已知:如图, 于 , 于G, .
求证: 平分
18.在学习地理时,我们知道:“海拔越高,气温越低”,下表是海拔高度h(千米)与此高度处气温的关系.根据下表,回答以下问题:
海拔高度h(千米) 0 1 2 3 4 5 …
气温 20 14 8 2 …
(1)由表可知,距离地面高度每上升1千米,温度降低________摄氏度.
(2)写出气温t与海拔高度h的关系式;并求出当海拔高度是7千米时,其气温是多少?
(3)某航班飞机在执行飞行任务至一定高度时,驾驶舱突现险情,此时舱外气温为.两名飞行员冷静应对,创造了世界航空史上的奇迹,请你计算出该飞机发生险情时的海拔高度(假设当时所在位置的地面温度为).
六、实践探究题
19.【问题情境】数学活动课上老师提到我们身边很多事物都蕴含着数学知识,班上的数学兴趣小组决定趁着游玩之便对摩天轮进行实地调研.摩天轮位于儿童公园内,摩天轮上均匀分布60个吊舱,顺时针旋转一周需要20分钟.
【实践过程】小组成员使用秒表和手机的测距功能,记录某个吊舱从最低点旋转到不同位置距地面的高度和所用的时间的数据,并绘制图像如图1.
【问题研究】请根据图1中信息回答:
(1)在这个变化过程中,自变量是______,因变量是______;
(2)摩天轮最高点距地面______(米),摩天轮最低点距地面______(米);
【问题解决】
(3)如图2,摩天轮某个吊舱从点A旋转到点B需6分钟,那么请你求出这个吊舱从点顺时针旋转到点所走的路径的长度.(结果保留)
答案解析部分
1.【答案】C
【知识点】用关系式表示变量间的关系
2.【答案】D
【知识点】常量、变量
3.【答案】B
【知识点】常量、变量
4.【答案】D
【知识点】常量、变量
5.【答案】D
【知识点】常量、变量
6.【答案】
【知识点】用关系式表示变量间的关系
7.【答案】
【知识点】用关系式表示变量间的关系
8.【答案】
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
9.【答案】450
【知识点】用表格表示变量间的关系
10.【答案】
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
11.【答案】
【知识点】用关系式表示变量间的关系
12.【答案】(1)
(2)
(3)
(4)
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
13.【答案】(1)下落的角度h与经过的时间t之间的关系,自变量:经过的时间t,因变量:下落的高度h;(2);(3)这颗果子开始下落时离地面高度为20.6m.
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
14.【答案】(1),甲;
(2),
(3)
【知识点】用图象表示变量间的关系
15.【答案】(1)44
(2)解:水池中水量随放水时间的增长而减少.
(3)解:,
答:当放水时间为7分镫时,水池中水量是.
【知识点】用表格表示变量间的关系
16.【答案】(1)3000个字
(2)所需时间随着每分钟打字的个数的减小而增大
(3),
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
17.【答案】(1)解:①根据题意可知,上表反映了岩层的深度与岩层的温度两个变量之间的关系,其中岩层的深度为自变量,岩层的温度为因变量;②观察表格可以发现:深度每增加 ,温度增加35摄氏度;③当h=10km时,t=370℃;
(2)证明:∵ 于 , 于
∴AD∥EG
∴∠E=∠CAD,∠AFE=∠DAB
又∵∠E=∠AFE
∴∠CAD=∠DAB
∴AD平分∠BAC
【知识点】常量、变量;平行线的性质
18.【答案】(1)6
(2)解:气温与海拔高度的关系式:,
当时,,
(3)解:当时,即,
解得:,
答:该飞机发生险情时的海拔高度9.7千米.
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
19.【答案】(1)t,h;(2)108,3;(3)所走的路径的长度是米
【知识点】用图象表示变量间的关系
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.1 常量与变量
一、单选题
1.某校八年级(4)班用150元购买了某品牌乒乓球个,该品牌乒乓球的单价是元/个,其函数关系式为,在这个问题中,变量是( )
A.150,x B.150,y C.x,y D.,
2.在利用太阳能热水器来加热水的过程中,热水器里的水温会随着太阳照射时间的长短而变化,在这个变化过程中,自变量是( )
A.热水器里的水温 B.太阳光的强弱
C.热水器的容积 D.太阳照射时间的长短
3.甲、乙两地相距50千米,若一辆汽车以50千米/时的速度从甲地到乙地,则汽车距乙地的路程s(千米)与行驶的时间t(时)之间的关系式s=50-50t中,常量的个数为( )
A.1 B.2 C.3 D.4
4.对于圆的周长公式,下列说法正确的是( )
A.C是变量,是常量 B.C是常量,是变量
C.C是变量,是常量 D.C是变量,是常量
5.如图是加油机上的数据显示牌,其中的变量是( )
A.金额 B.单价 C.油量 D.金额和油量
二、填空题
6.某人购进一批苹果,到市场零售,已知卖出苹果数量千克与售价元的关系如下表:
数量千克 2 3 4 5
售价元
用x表示y的关系式可表示为 .
7.某公司制作毕业纪念册的收费标准是:每册收取材料费4元,则总收费y(元)与制作纪念册的册数x (册)之间的关系式为 .
8.某汽车生产厂对其生产的型汽车进行油耗试验(油箱已加满),试验中汽车为匀速行驶,在行驶过程中,油箱的余油量(升)与行驶时间(小时)之间的关系如下表:
(小时) 0 1 2 3
(升) 80 72 64 56
则与之间的关系式为 .
9.我国首辆火星车正式被命名为“祝融”,为应对极限温度环境,火星车使用的是新型隔温材料——纳米气凝胶,该材料导热率与温度的关系如表:
温度 100 150 200 250 300 350 400
导热率
根据表格中两者的对应关系,若导热率为,则温度为 .
10.某水果店卖出的苹果数量(千克)与售价(元)之间的关系如下表:
苹果数量x(千克) 0.5 1 1.5 2 2.5 3 3.5 …
售价y(元) 2.5 5 7.5 10 12.5 15 17.5 …
上表反映了两个变量之间的关系,则与的关系式为
11.将一根长为的铁丝制作成一个长方形,则这个长方形的长y()与宽x()之间的关系式为 .(不用写出自变量x的取值范围)
三、计算题
12.探索计算:弹簧挂上物体后会伸长.已知一弹簧的长度()与所挂物体的质量()之间的关系如下表:
所挂物体的质量/
弹簧的长度/
(1)当所挂物体的质量为时,弹簧的长度是_______________________;
(2)在弹性限度内如果所挂物体的质量为,弹簧的长度为,根据上表直接写出与的关系式_____________;
(3)当所挂物体的质量为时,请求出弹簧的长度;
(4)如果弹簧的最大长度为,那么该弹簧最多能挂质量为多少的物体?
13.果实成熟从树上落到地面,它下落的高度与经过的时间有如下的关系:
时间t/秒 0.5 0.6 0.7 0.8 0.9 …
高度h/米 …
(1)上表反映了哪两个变量之间的关系?其中自变量是什么?因变量是什么?
(2)请你按照表中呈现的规律,列出果子下落的高度(米)与时间(秒)之间的关系式;
(3)现有一颗果子经过2秒后离地面一米,请计算这颗果子开始下落时离地面的高度是多少米?
四、解答题
14.全球首次“人机共跑”半程马拉松于年月日在北京完赛,经过时分秒的奔跑,机器人“天工”率先冲过终点拱门,夺得桂冠.受到该项赛事启发,某中学机器人兴趣小组也举办了“机器人竞速比赛”,比赛中甲、乙两台机器人的赛跑路程和赛跑时间之间的关系如图所示,请根据图象信息回答下列问题:
(1)本次比赛全程是___________,机器人___________先到达终点;
(2)机器人甲的平均速度是___________,其路程和时间的关系式是___________;
(3)机器人乙由于故障在途中停留了___________,恢复运行后,机器人乙的速度___________机器人甲的速度.(填“”“”或“”)
15.一个蓄水池有水,打开放水闸门放水,水池里的水和放水时间的关系如表,回答下面问题:
放水时间(分钟) 1 2 3 4 5 …
水池中水量 48 46 42 40 …
(1)如图所示,将表格补充完整; .
(2)根据表格中的数据,说明在放完水前,水池中水量是随放水时间的增长而怎样变化的?
(3)当放水时间为7分钟时,水池中水量是多少立方米?
五、综合题
16.王老师打一篇演讲稿,每分钟打字的个数与所需时间之间的关系如下表:
每分钟打字的个数(个) 120 100 75 60
所需时间(分) 25 30 40 50
(1)这篇演讲稿共有多少字?
(2)所需时间是怎样随着每分钟打字的个数的变化而变化?
(3)用表示所需时间,用表示每分钟打字的个数,用式子表示与的关系.与成什么比例关系?当时,求的值.
17.
(1)地表以下的岩层的温度和它所处的深度有以下关系:
①上表反映了两个变量之间的关系,哪个是自变量?哪个是因变量?
②深度每增加 ,温度增加多少摄氏度?
③估计 深处的岩层温度是多少摄氏度.
(2)已知:如图, 于 , 于G, .
求证: 平分
18.在学习地理时,我们知道:“海拔越高,气温越低”,下表是海拔高度h(千米)与此高度处气温的关系.根据下表,回答以下问题:
海拔高度h(千米) 0 1 2 3 4 5 …
气温 20 14 8 2 …
(1)由表可知,距离地面高度每上升1千米,温度降低________摄氏度.
(2)写出气温t与海拔高度h的关系式;并求出当海拔高度是7千米时,其气温是多少?
(3)某航班飞机在执行飞行任务至一定高度时,驾驶舱突现险情,此时舱外气温为.两名飞行员冷静应对,创造了世界航空史上的奇迹,请你计算出该飞机发生险情时的海拔高度(假设当时所在位置的地面温度为).
六、实践探究题
19.【问题情境】数学活动课上老师提到我们身边很多事物都蕴含着数学知识,班上的数学兴趣小组决定趁着游玩之便对摩天轮进行实地调研.摩天轮位于儿童公园内,摩天轮上均匀分布60个吊舱,顺时针旋转一周需要20分钟.
【实践过程】小组成员使用秒表和手机的测距功能,记录某个吊舱从最低点旋转到不同位置距地面的高度和所用的时间的数据,并绘制图像如图1.
【问题研究】请根据图1中信息回答:
(1)在这个变化过程中,自变量是______,因变量是______;
(2)摩天轮最高点距地面______(米),摩天轮最低点距地面______(米);
【问题解决】
(3)如图2,摩天轮某个吊舱从点A旋转到点B需6分钟,那么请你求出这个吊舱从点顺时针旋转到点所走的路径的长度.(结果保留)
答案解析部分
1.【答案】C
【知识点】用关系式表示变量间的关系
2.【答案】D
【知识点】常量、变量
3.【答案】B
【知识点】常量、变量
4.【答案】D
【知识点】常量、变量
5.【答案】D
【知识点】常量、变量
6.【答案】
【知识点】用关系式表示变量间的关系
7.【答案】
【知识点】用关系式表示变量间的关系
8.【答案】
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
9.【答案】450
【知识点】用表格表示变量间的关系
10.【答案】
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
11.【答案】
【知识点】用关系式表示变量间的关系
12.【答案】(1)
(2)
(3)
(4)
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
13.【答案】(1)下落的角度h与经过的时间t之间的关系,自变量:经过的时间t,因变量:下落的高度h;(2);(3)这颗果子开始下落时离地面高度为20.6m.
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
14.【答案】(1),甲;
(2),
(3)
【知识点】用图象表示变量间的关系
15.【答案】(1)44
(2)解:水池中水量随放水时间的增长而减少.
(3)解:,
答:当放水时间为7分镫时,水池中水量是.
【知识点】用表格表示变量间的关系
16.【答案】(1)3000个字
(2)所需时间随着每分钟打字的个数的减小而增大
(3),
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
17.【答案】(1)解:①根据题意可知,上表反映了岩层的深度与岩层的温度两个变量之间的关系,其中岩层的深度为自变量,岩层的温度为因变量;②观察表格可以发现:深度每增加 ,温度增加35摄氏度;③当h=10km时,t=370℃;
(2)证明:∵ 于 , 于
∴AD∥EG
∴∠E=∠CAD,∠AFE=∠DAB
又∵∠E=∠AFE
∴∠CAD=∠DAB
∴AD平分∠BAC
【知识点】常量、变量;平行线的性质
18.【答案】(1)6
(2)解:气温与海拔高度的关系式:,
当时,,
(3)解:当时,即,
解得:,
答:该飞机发生险情时的海拔高度9.7千米.
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
19.【答案】(1)t,h;(2)108,3;(3)所走的路径的长度是米
【知识点】用图象表示变量间的关系
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
