5.5一次函数的简单应用 同步练习(含答案)
文档属性
| 名称 | 5.5一次函数的简单应用 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 541.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 19:45:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
5.5 一次函数的简单应用
一、单选题
1.一次函数的图像如图所示,当时,x的取值范围是( )
A. B. C. D.
2.如图,直线和相交于点,则不等式的解集为( )
A. B. C. D.
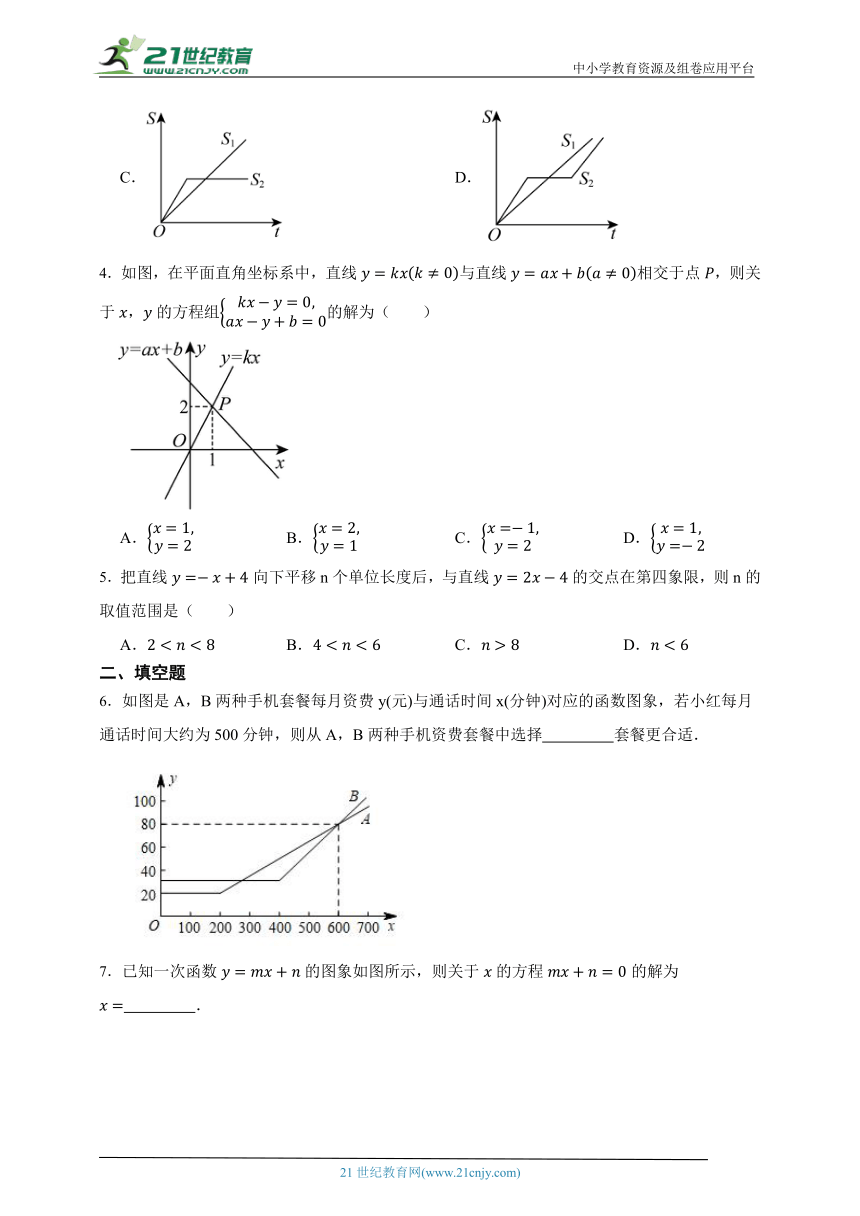
3.兄弟两人沿五四广场的木栈道跑步,领先的哥哥看弟弟跑得慢,就停下来看风景,过了一会发现弟弟跑前面去了,急忙追赶,结果比弟弟提前到达终点.用,分别表示哥哥和弟弟所跑的路程,t为跑步时间,则下列图象与故事情节相吻合的是( )
A. B.
C. D.
4.如图,在平面直角坐标系中,直线与直线相交于点,则关于,的方程组的解为( )
A. B. C. D.
5.把直线向下平移n个单位长度后,与直线的交点在第四象限,则n的取值范围是( )
A. B. C. D.
二、填空题
6.如图是A,B两种手机套餐每月资费y(元)与通话时间x(分钟)对应的函数图象,若小红每月通话时间大约为500分钟,则从A,B两种手机资费套餐中选择 套餐更合适.
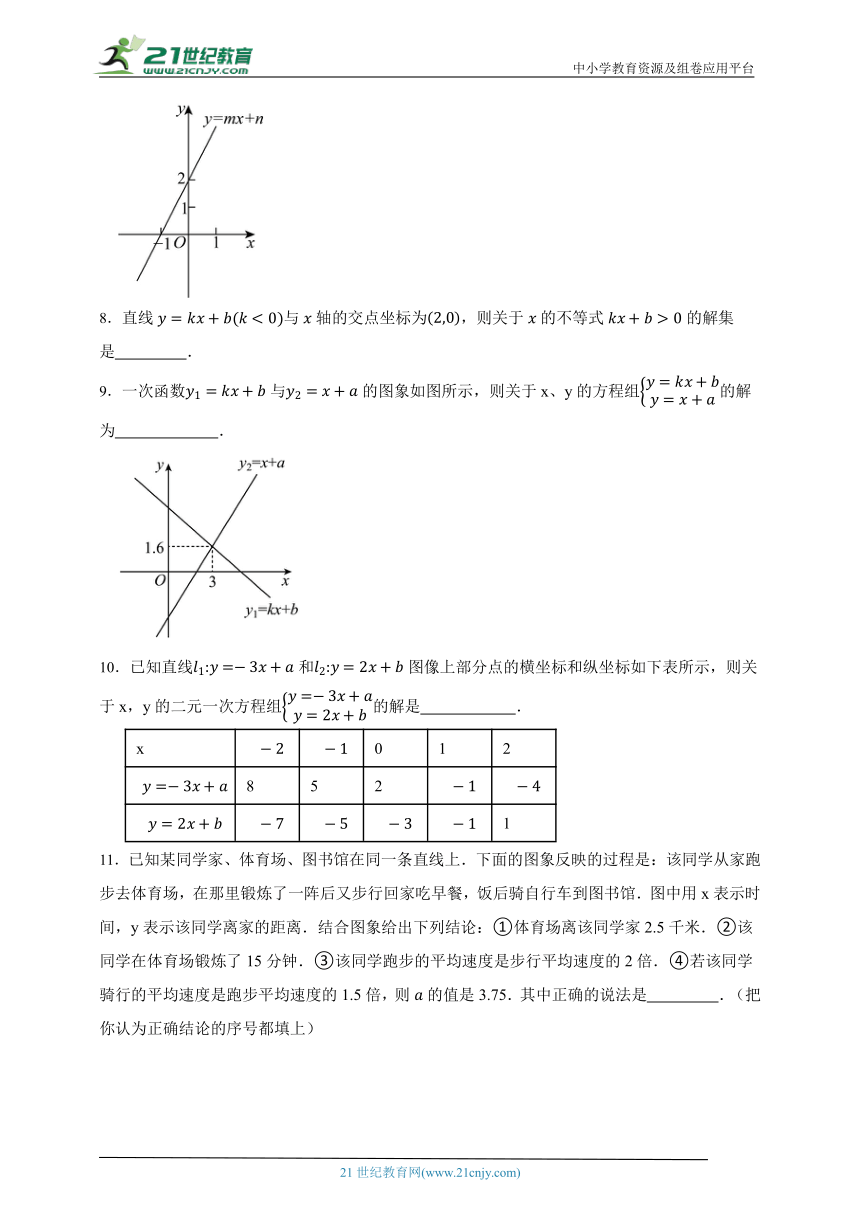
7.已知一次函数的图象如图所示,则关于的方程的解为 .
8.直线与轴的交点坐标为,则关于的不等式的解集是 .
9.一次函数与的图象如图所示,则关于x、y的方程组的解为 .
10.已知直线和图像上部分点的横坐标和纵坐标如下表所示,则关于x,y的二元一次方程组的解是 .
x 0 1 2
8 5 2
1
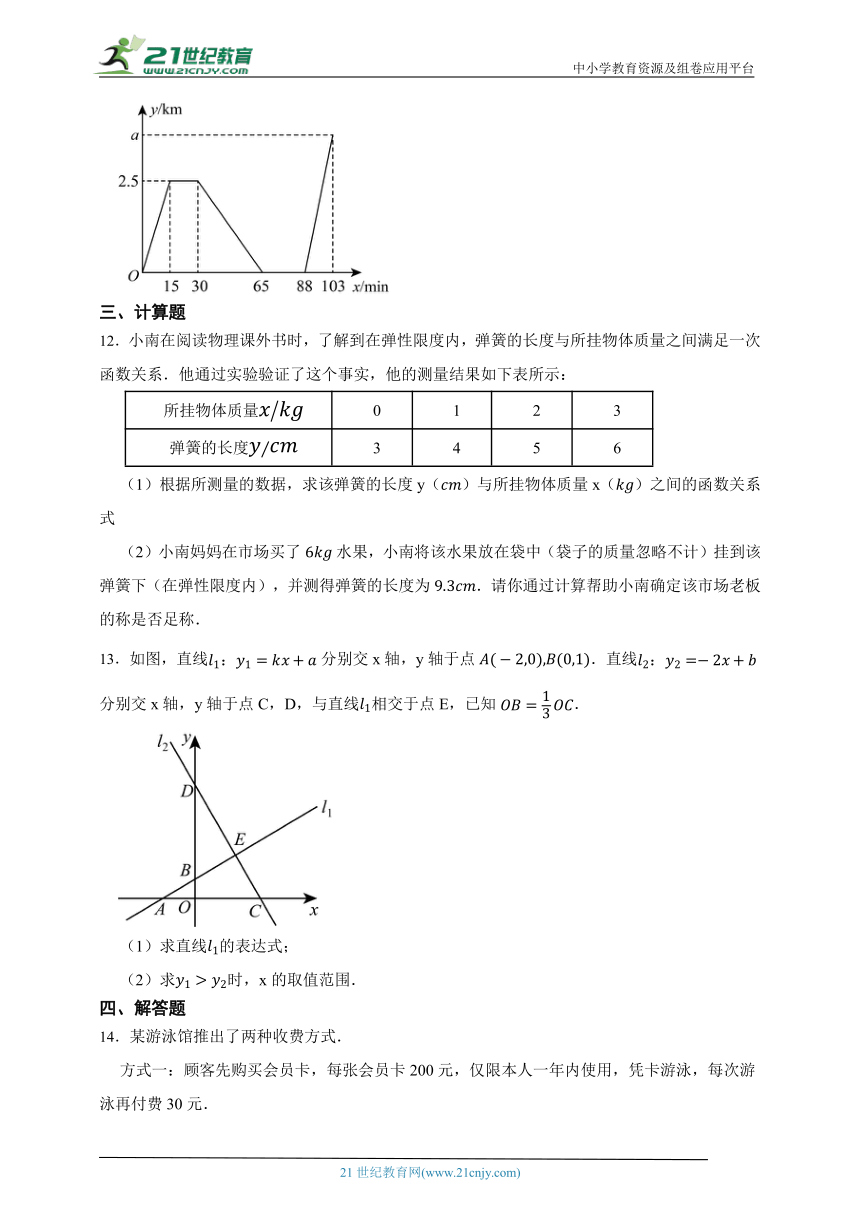
11.已知某同学家、体育场、图书馆在同一条直线上.下面的图象反映的过程是:该同学从家跑步去体育场,在那里锻炼了一阵后又步行回家吃早餐,饭后骑自行车到图书馆.图中用x表示时间,y表示该同学离家的距离.结合图象给出下列结论:①体育场离该同学家2.5千米.②该同学在体育场锻炼了15分钟.③该同学跑步的平均速度是步行平均速度的2倍.④若该同学骑行的平均速度是跑步平均速度的1.5倍,则的值是3.75.其中正确的说法是 .(把你认为正确结论的序号都填上)
三、计算题
12.小南在阅读物理课外书时,了解到在弹性限度内,弹簧的长度与所挂物体质量之间满足一次函数关系.他通过实验验证了这个事实,他的测量结果如下表所示:
所挂物体质量 0 1 2 3
弹簧的长度 3 4 5 6
(1)根据所测量的数据,求该弹簧的长度y()与所挂物体质量x()之间的函数关系式
(2)小南妈妈在市场买了水果,小南将该水果放在袋中(袋子的质量忽略不计)挂到该弹簧下(在弹性限度内),并测得弹簧的长度为.请你通过计算帮助小南确定该市场老板的称是否足称.
13.如图,直线分别交x轴,y轴于点.直线分别交x轴,y轴于点C,D,与直线相交于点E,已知.
(1)求直线的表达式;
(2)求时,x的取值范围.
四、解答题
14.某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.
设小亮在一年内来此游泳馆的次数为x次,选择方式一的总费用为y1(元),选择方式二的总费用为y2(元).
(1)请分别写出y1,y2与x之间的函数表达式.
(2)若小亮一年内来此游泳馆的次数为15次,选择哪种方式比较划算?
(3)若小亮计划拿出1400元用于在此游泳馆游泳,采用哪种付费方式更划算?
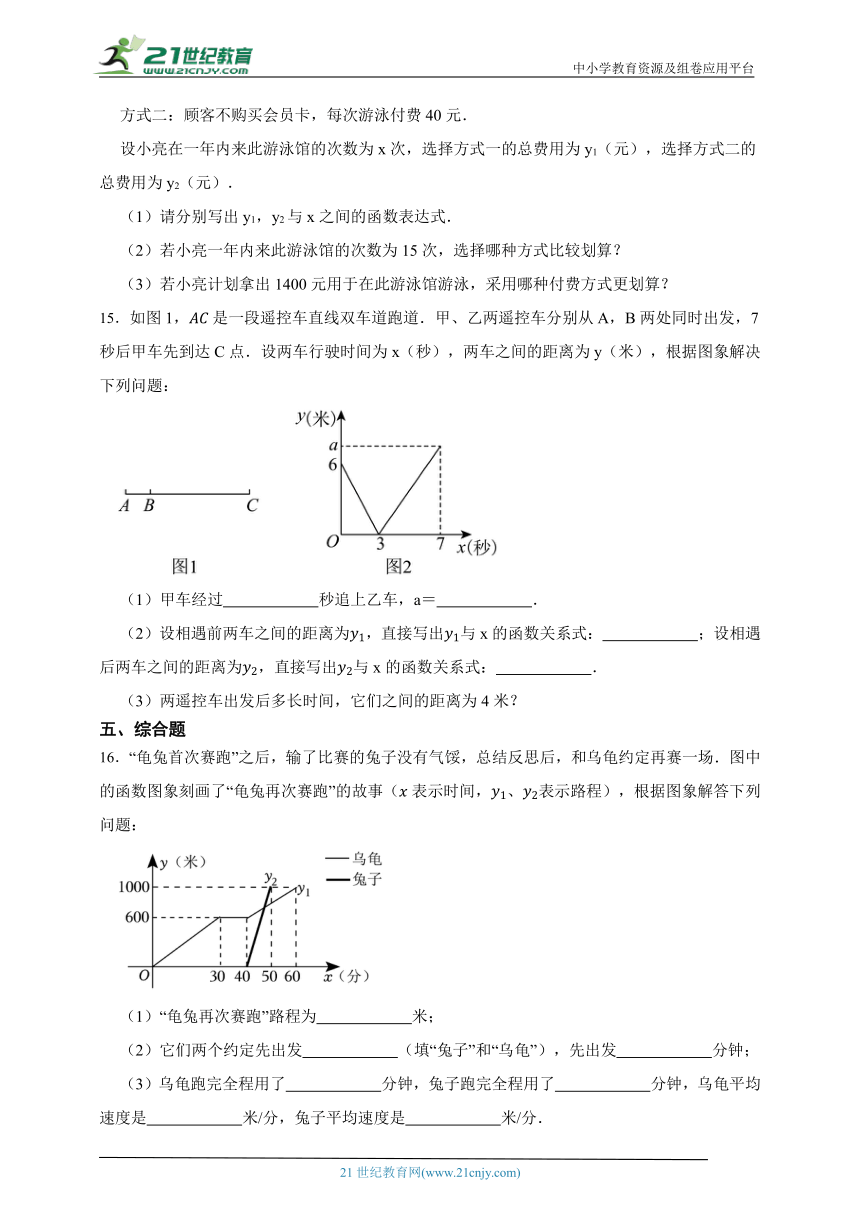
15.如图1,是一段遥控车直线双车道跑道.甲、乙两遥控车分别从A,B两处同时出发,7秒后甲车先到达C点.设两车行驶时间为x(秒),两车之间的距离为y(米),根据图象解决下列问题:
(1)甲车经过 秒追上乙车,a= .
(2)设相遇前两车之间的距离为,直接写出与x的函数关系式: ;设相遇后两车之间的距离为,直接写出与x的函数关系式: .
(3)两遥控车出发后多长时间,它们之间的距离为4米?
五、综合题
16.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(表示时间,、表示路程),根据图象解答下列问题:
(1)“龟兔再次赛跑”路程为 米;
(2)它们两个约定先出发 (填“兔子”和“乌龟”),先出发 分钟;
(3)乌龟跑完全程用了 分钟,兔子跑完全程用了 分钟,乌龟平均速度是 米/分,兔子平均速度是 米/分.
17.为了锻炼身体增强体质,小何同学在某周末上午9时骑自行车离开家去绿道锻炼,15时回家,已知小何离家的距离s(km)与时间t(h)之间的关系如图所示.
根据图象解答下列问题:
(1)写出小何离家的最远距离;
(2)小何途中共休息了几次,每次休息多长时间?
(3)小何由离家最远的地方返回家时的平均速度是多少?
18.下图是小明从家到超市的距离与时间之间关系的图象.
(1)图中反映了哪两个变量之间的关系?
(2)超市离家多远?
(3)小明从超市返回家用了多少时间?
(4)小明从家到超市时的平均速度是多少?
六、实践探究题
19.小明看到一个水龙头因损坏而不断地滴水,为探究其漏水造成的浪费情况,他将一个带有刻度的量筒放在水龙头下面接水,每隔一分钟记录量筒中的总水量,得到如表的一组数据:
时间t(单位:分) 1 2 3 4 5 ……
总水量y(单位:毫升) 5 10 15 20 25 ……
(1)探究:
在这个变化过程中,______是自变量,______是因变量;
(2)应用:
①第6分时量筒中的总水量是______毫升;
②小明查阅资料发现:若儿童年龄在10岁以上,家长需要给儿童每天摄入1800毫升的饮水量,请你帮小明计算这个水龙头一个月(按30天计)的漏水量可供一个儿童饮用约多少天?
答案解析部分
1.【答案】D
【知识点】一次函数与不等式(组)的关系
2.【答案】B
【知识点】一次函数的概念;一次函数与不等式(组)的关系
3.【答案】A
【知识点】通过函数图象获取信息
4.【答案】A
【知识点】一次函数与二元一次方程(组)的关系
5.【答案】A
【知识点】解一元一次不等式组;一次函数与二元一次方程(组)的关系;一次函数图象的平移变换
6.【答案】B
【知识点】一次函数的实际应用;通过函数图象获取信息
7.【答案】
【知识点】一次函数与一元一次方程的关系
8.【答案】
【知识点】一次函数与不等式(组)的关系
9.【答案】
【知识点】一次函数与二元一次方程(组)的关系
10.【答案】
【知识点】一次函数与二元一次方程(组)的关系
11.【答案】①②④
【知识点】通过函数图象获取信息
12.【答案】(1);
(2)该市场老板的称足称.
【知识点】待定系数法求一次函数解析式;一次函数的其他应用
13.【答案】(1)
(2)
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系
14.【答案】(1)方式一费用为y1=30x+200,方式二的费用为y2=40x;(2)方式二划算;(3)采用方式一更划算.
【知识点】一次函数的其他应用
15.【答案】(1)3,8
(2),;
(3)两遥控车出发后1秒或5秒.
【知识点】一次函数的实际应用-行程问题
16.【答案】(1)1000
(2)乌龟,40
(3)60,10,,100
【知识点】通过函数图象获取信息;一次函数的实际应用-行程问题
17.【答案】(1)解:利用图象的纵坐标得出小何骑自行车离家的最远距离是;
(2)根据图象得出有两段时间纵坐标不变,得出途中小何共休息了2次;利用横坐标得出休息时间为:0.5小时和1小时;
(3)解:∵返回时所走路程为,使用时间为2小时,
∴返回时的平均速度为:.
【知识点】通过函数图象获取信息
18.【答案】(1)小明从家到超市的距离和时间
(2)900米
(3)15分钟
(4)米/分
【知识点】通过函数图象获取信息;用图象表示变量间的关系
19.【答案】(1)时间t;总水量y
(2)①30;②120天
【知识点】函数自变量的取值范围;用关系式表示变量间的关系;一次函数的其他应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.5 一次函数的简单应用
一、单选题
1.一次函数的图像如图所示,当时,x的取值范围是( )
A. B. C. D.
2.如图,直线和相交于点,则不等式的解集为( )
A. B. C. D.
3.兄弟两人沿五四广场的木栈道跑步,领先的哥哥看弟弟跑得慢,就停下来看风景,过了一会发现弟弟跑前面去了,急忙追赶,结果比弟弟提前到达终点.用,分别表示哥哥和弟弟所跑的路程,t为跑步时间,则下列图象与故事情节相吻合的是( )
A. B.
C. D.
4.如图,在平面直角坐标系中,直线与直线相交于点,则关于,的方程组的解为( )
A. B. C. D.
5.把直线向下平移n个单位长度后,与直线的交点在第四象限,则n的取值范围是( )
A. B. C. D.
二、填空题
6.如图是A,B两种手机套餐每月资费y(元)与通话时间x(分钟)对应的函数图象,若小红每月通话时间大约为500分钟,则从A,B两种手机资费套餐中选择 套餐更合适.
7.已知一次函数的图象如图所示,则关于的方程的解为 .
8.直线与轴的交点坐标为,则关于的不等式的解集是 .
9.一次函数与的图象如图所示,则关于x、y的方程组的解为 .
10.已知直线和图像上部分点的横坐标和纵坐标如下表所示,则关于x,y的二元一次方程组的解是 .
x 0 1 2
8 5 2
1
11.已知某同学家、体育场、图书馆在同一条直线上.下面的图象反映的过程是:该同学从家跑步去体育场,在那里锻炼了一阵后又步行回家吃早餐,饭后骑自行车到图书馆.图中用x表示时间,y表示该同学离家的距离.结合图象给出下列结论:①体育场离该同学家2.5千米.②该同学在体育场锻炼了15分钟.③该同学跑步的平均速度是步行平均速度的2倍.④若该同学骑行的平均速度是跑步平均速度的1.5倍,则的值是3.75.其中正确的说法是 .(把你认为正确结论的序号都填上)
三、计算题
12.小南在阅读物理课外书时,了解到在弹性限度内,弹簧的长度与所挂物体质量之间满足一次函数关系.他通过实验验证了这个事实,他的测量结果如下表所示:
所挂物体质量 0 1 2 3
弹簧的长度 3 4 5 6
(1)根据所测量的数据,求该弹簧的长度y()与所挂物体质量x()之间的函数关系式
(2)小南妈妈在市场买了水果,小南将该水果放在袋中(袋子的质量忽略不计)挂到该弹簧下(在弹性限度内),并测得弹簧的长度为.请你通过计算帮助小南确定该市场老板的称是否足称.
13.如图,直线分别交x轴,y轴于点.直线分别交x轴,y轴于点C,D,与直线相交于点E,已知.
(1)求直线的表达式;
(2)求时,x的取值范围.
四、解答题
14.某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.
设小亮在一年内来此游泳馆的次数为x次,选择方式一的总费用为y1(元),选择方式二的总费用为y2(元).
(1)请分别写出y1,y2与x之间的函数表达式.
(2)若小亮一年内来此游泳馆的次数为15次,选择哪种方式比较划算?
(3)若小亮计划拿出1400元用于在此游泳馆游泳,采用哪种付费方式更划算?
15.如图1,是一段遥控车直线双车道跑道.甲、乙两遥控车分别从A,B两处同时出发,7秒后甲车先到达C点.设两车行驶时间为x(秒),两车之间的距离为y(米),根据图象解决下列问题:
(1)甲车经过 秒追上乙车,a= .
(2)设相遇前两车之间的距离为,直接写出与x的函数关系式: ;设相遇后两车之间的距离为,直接写出与x的函数关系式: .
(3)两遥控车出发后多长时间,它们之间的距离为4米?
五、综合题
16.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(表示时间,、表示路程),根据图象解答下列问题:
(1)“龟兔再次赛跑”路程为 米;
(2)它们两个约定先出发 (填“兔子”和“乌龟”),先出发 分钟;
(3)乌龟跑完全程用了 分钟,兔子跑完全程用了 分钟,乌龟平均速度是 米/分,兔子平均速度是 米/分.
17.为了锻炼身体增强体质,小何同学在某周末上午9时骑自行车离开家去绿道锻炼,15时回家,已知小何离家的距离s(km)与时间t(h)之间的关系如图所示.
根据图象解答下列问题:
(1)写出小何离家的最远距离;
(2)小何途中共休息了几次,每次休息多长时间?
(3)小何由离家最远的地方返回家时的平均速度是多少?
18.下图是小明从家到超市的距离与时间之间关系的图象.
(1)图中反映了哪两个变量之间的关系?
(2)超市离家多远?
(3)小明从超市返回家用了多少时间?
(4)小明从家到超市时的平均速度是多少?
六、实践探究题
19.小明看到一个水龙头因损坏而不断地滴水,为探究其漏水造成的浪费情况,他将一个带有刻度的量筒放在水龙头下面接水,每隔一分钟记录量筒中的总水量,得到如表的一组数据:
时间t(单位:分) 1 2 3 4 5 ……
总水量y(单位:毫升) 5 10 15 20 25 ……
(1)探究:
在这个变化过程中,______是自变量,______是因变量;
(2)应用:
①第6分时量筒中的总水量是______毫升;
②小明查阅资料发现:若儿童年龄在10岁以上,家长需要给儿童每天摄入1800毫升的饮水量,请你帮小明计算这个水龙头一个月(按30天计)的漏水量可供一个儿童饮用约多少天?
答案解析部分
1.【答案】D
【知识点】一次函数与不等式(组)的关系
2.【答案】B
【知识点】一次函数的概念;一次函数与不等式(组)的关系
3.【答案】A
【知识点】通过函数图象获取信息
4.【答案】A
【知识点】一次函数与二元一次方程(组)的关系
5.【答案】A
【知识点】解一元一次不等式组;一次函数与二元一次方程(组)的关系;一次函数图象的平移变换
6.【答案】B
【知识点】一次函数的实际应用;通过函数图象获取信息
7.【答案】
【知识点】一次函数与一元一次方程的关系
8.【答案】
【知识点】一次函数与不等式(组)的关系
9.【答案】
【知识点】一次函数与二元一次方程(组)的关系
10.【答案】
【知识点】一次函数与二元一次方程(组)的关系
11.【答案】①②④
【知识点】通过函数图象获取信息
12.【答案】(1);
(2)该市场老板的称足称.
【知识点】待定系数法求一次函数解析式;一次函数的其他应用
13.【答案】(1)
(2)
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系
14.【答案】(1)方式一费用为y1=30x+200,方式二的费用为y2=40x;(2)方式二划算;(3)采用方式一更划算.
【知识点】一次函数的其他应用
15.【答案】(1)3,8
(2),;
(3)两遥控车出发后1秒或5秒.
【知识点】一次函数的实际应用-行程问题
16.【答案】(1)1000
(2)乌龟,40
(3)60,10,,100
【知识点】通过函数图象获取信息;一次函数的实际应用-行程问题
17.【答案】(1)解:利用图象的纵坐标得出小何骑自行车离家的最远距离是;
(2)根据图象得出有两段时间纵坐标不变,得出途中小何共休息了2次;利用横坐标得出休息时间为:0.5小时和1小时;
(3)解:∵返回时所走路程为,使用时间为2小时,
∴返回时的平均速度为:.
【知识点】通过函数图象获取信息
18.【答案】(1)小明从家到超市的距离和时间
(2)900米
(3)15分钟
(4)米/分
【知识点】通过函数图象获取信息;用图象表示变量间的关系
19.【答案】(1)时间t;总水量y
(2)①30;②120天
【知识点】函数自变量的取值范围;用关系式表示变量间的关系;一次函数的其他应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
