第1章 三角形的初步知识 章末复习(含答案)
文档属性
| 名称 | 第1章 三角形的初步知识 章末复习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 479.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 19:58:26 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第1章 三角形的初步知识
一、单选题
1.如图,在中,,以为圆心,任意长为半径画弧, 分别交,于点,, 再分别以,,为圆心, 大于 长为半径画弧,两弧交于点,作射线, 交于点. 已知,,的面积为( )
A. B. C. D.
2.下列哪个图形具有稳定性( )
A. B.
C. D.
3.如图,在中,,,,分别是的高线、中线和角平分线,下列结论错误的是( )
A. B.
C. D.
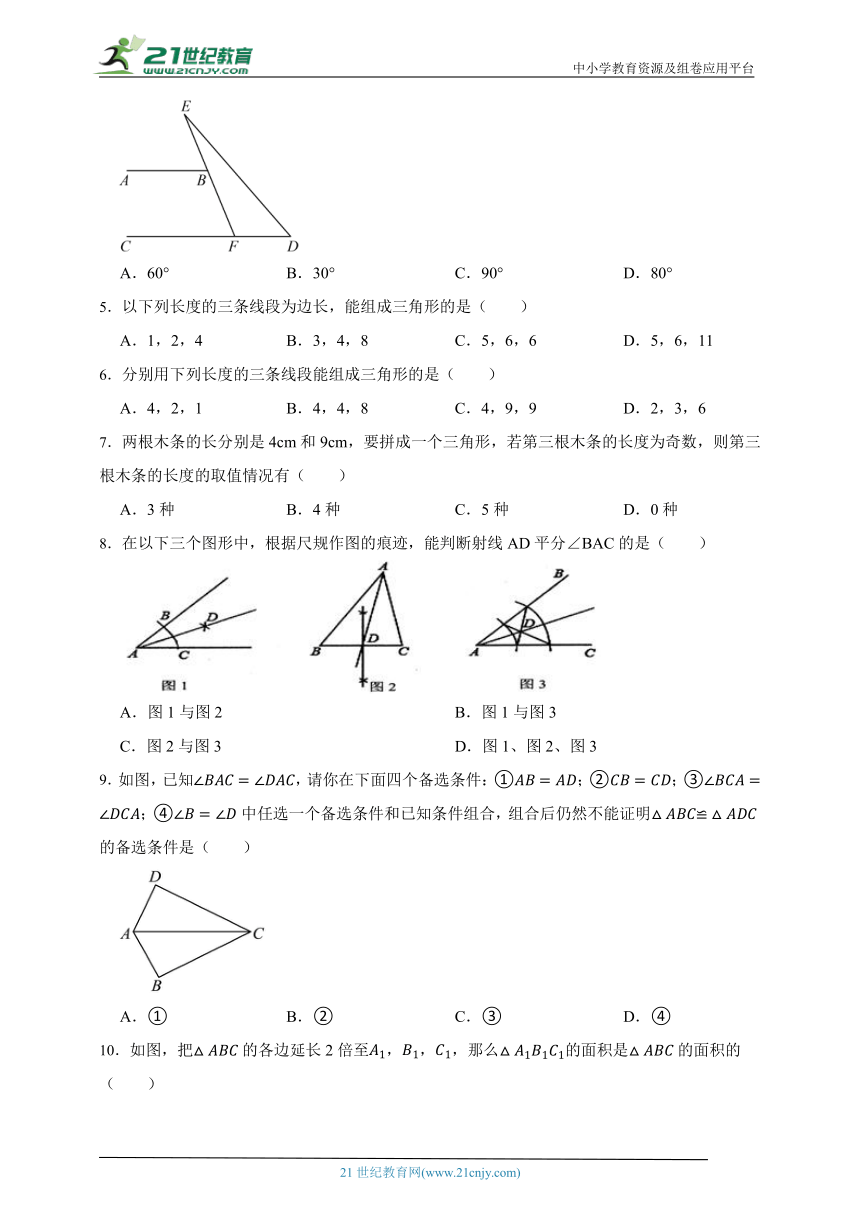
4.如图,在中,点C在的延长线上,点B在上,且,,则的度数为( )
A.60° B.30° C.90° D.80°
5.以下列长度的三条线段为边长,能组成三角形的是( )
A.1,2,4 B.3,4,8 C.5,6,6 D.5,6,11
6.分别用下列长度的三条线段能组成三角形的是( )
A.4,2,1 B.4,4,8 C.4,9,9 D.2,3,6
7.两根木条的长分别是4cm和9cm,要拼成一个三角形,若第三根木条的长度为奇数,则第三根木条的长度的取值情况有( )
A.3种 B.4种 C.5种 D.0种
8.在以下三个图形中,根据尺规作图的痕迹,能判断射线AD平分∠BAC的是( )
A.图1与图2 B.图1与图3
C.图2与图3 D.图1、图2、图3
9.如图,已知,请你在下面四个备选条件:①;②;③;④中任选一个备选条件和已知条件组合,组合后仍然不能证明的备选条件是( )
A.① B.② C.③ D.④
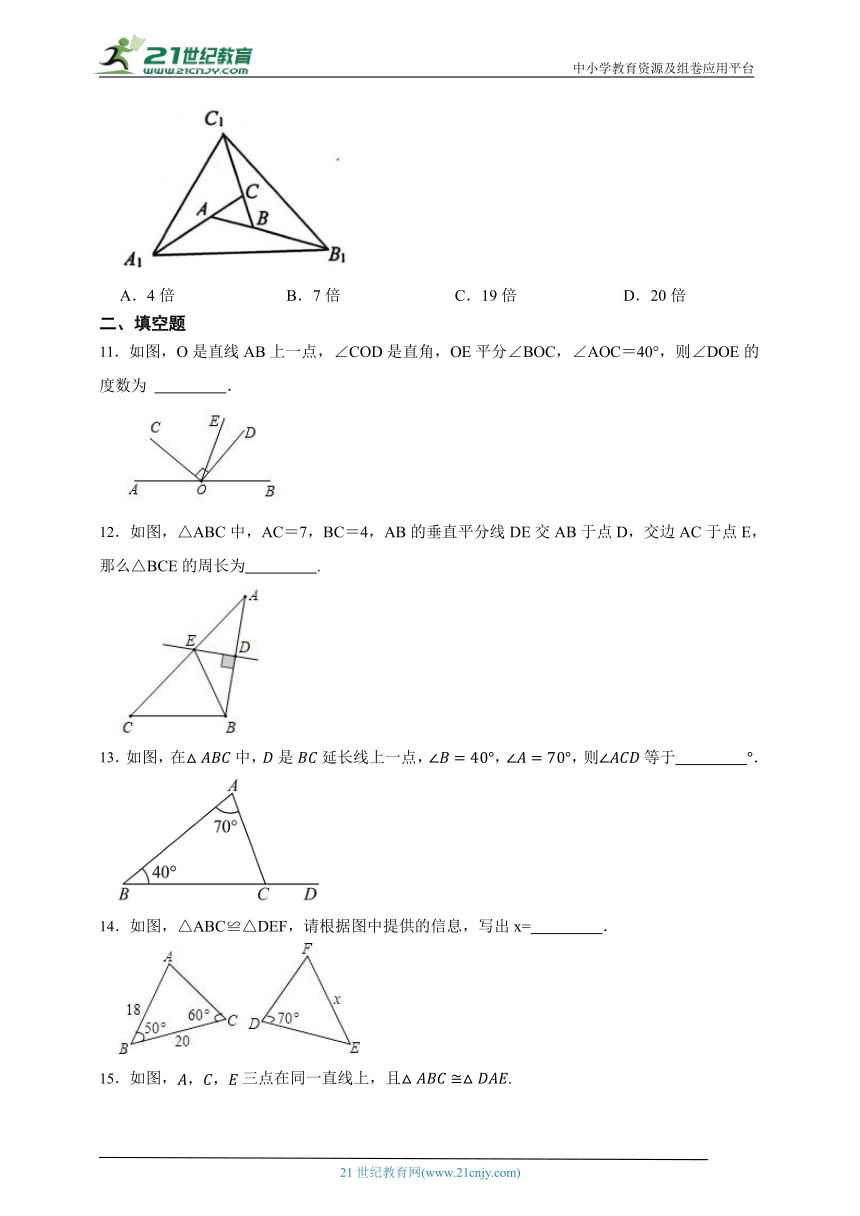
10.如图,把的各边延长2倍至,,,那么的面积是的面积的( )
A.4倍 B.7倍 C.19倍 D.20倍
二、填空题
11.如图,O是直线AB上一点,∠COD是直角,OE平分∠BOC,∠AOC=40°,则∠DOE的度数为 .
12.如图,△ABC中,AC=7,BC=4,AB的垂直平分线DE交AB于点D,交边AC于点E,那么△BCE的周长为 .
13.如图,在中,是延长线上一点,,,则等于 .
14.如图,△ABC≌△DEF,请根据图中提供的信息,写出x= .
15.如图,三点在同一直线上,且.
⑴若,则 ;
⑵当 °时,.
16.容器中有“O、P、Q”三种颗粒,若相同种类的颗粒发生碰撞,则会变成1个“P颗粒;若不同种类的颗粒发生碰撞,则会变成另一种颗粒,例如:一个“O”颗粒和一个“P”颗粒进行碰撞,则会变成一个“Q”颗粒.现有“O”颗粒11个,“P”颗粒10个,“Q”颗粒12个,经过两两碰撞后,最后一个颗粒一定不是 颗粒.
三、计算题
17.(1)已知a、b、c是的三边长,化简:;
(2)已知的三个内角度数之比为1∶1∶2,求这个三角形中最大角的度数.
18. 如图,直线AB//CD,BC平分∠ABD.
(1)若∠ABD=112°,求∠1的度数;
(2)若∠2= x°,求∠ABC的度数(请用含x的代数式表示).
四、解答题
19.如图,BD是△ABC的高线,∠A=60°,∠C=50°.求∠ABD与∠CBD的度数.
20.如图,在△ABC中,∠A=46°,CE是∠ACB的平分线,B,C,D在同一条直线上,DF∥EC,∠D=42°.求∠B的度数.
21.请在方格内画△ABC,使它的顶点都在格点上,且三边长分别为2,2 ,4 ,求①△ABC的面积;②求出最长边上高.
答案解析部分
1.【答案】B
【知识点】角平分线的性质;尺规作图-作角的平分线
2.【答案】C
【知识点】三角形的稳定性
3.【答案】D
【知识点】三角形的角平分线、中线和高;三角形内角和定理
4.【答案】D
【知识点】三角形外角的概念及性质;同位角的概念
5.【答案】C
【知识点】三角形三边关系
6.【答案】C
【知识点】三角形三边关系
7.【答案】A
【知识点】三角形三边关系
8.【答案】B
【知识点】三角形全等的判定-SAS;三角形全等的判定-AAS;尺规作图-作角的平分线
9.【答案】B
【知识点】三角形全等的判定
10.【答案】C
【知识点】三角形的面积
11.【答案】20°
【知识点】余角、补角及其性质;角平分线的性质
12.【答案】11
【知识点】线段垂直平分线的性质
13.【答案】
【知识点】三角形外角的概念及性质
14.【答案】20
【知识点】三角形全等及其性质
15.【答案】4;90
【知识点】平行线的性质;三角形全等及其性质
16.【答案】P
【知识点】推理与论证
17.【答案】(1);(2)这个三角形中最大角的度数为.
【知识点】三角形三边关系;三角形内角和定理;合并同类项法则及应用;化简含绝对值有理数
18.【答案】(1)解:∵BC平分∠ABD,
∴∠ABC=∠ABD=×112°=56°,
∵AB∥CD,
∴∠1=∠ABC=56°
(2)解:∵BC平分∠ABD,
∴∠ABC=∠DBC,
∵AB∥CD,
∴∠1=∠ABC=∠DBC,
∵∠2=∠CDB=180°-∠1-∠DBC=180°-2∠1=x°,
∴
【知识点】三角形内角和定理;角平分线的概念;两直线平行,内错角相等
19.【答案】解:∵BD是三角形ABC的高,
∴BD⊥AC,
∴∠ADB=∠CDB=90°,
又 ∠A=60°,∠C=50°,
∴∠ABD=180°-∠A-∠ADB=30°,∠CBD=180°-∠C-∠CDB=40°.
【知识点】三角形的角平分线、中线和高;三角形内角和定理
20.【答案】解:∵FD∥EC,
∴∠BCE=∠D=42°,
∵CE是∠ACB的平分线,
∴∠ACB=2∠BCE=84°,
∵∠A=46°,
∴∠B=180°-84°-46°=50°.
【知识点】平行线的性质;三角形的角平分线、中线和高;三角形内角和定理
21.【答案】解:①如图∵AC=2,BD=2∴S△ABC= AC×BD=2,②∵最长边AB=2 ,设最长边上的高为h,则S△ABC= AB×h=2,∴h= ,即最长边上高为 .
【知识点】实数在数轴上表示;三角形的面积
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1章 三角形的初步知识
一、单选题
1.如图,在中,,以为圆心,任意长为半径画弧, 分别交,于点,, 再分别以,,为圆心, 大于 长为半径画弧,两弧交于点,作射线, 交于点. 已知,,的面积为( )
A. B. C. D.
2.下列哪个图形具有稳定性( )
A. B.
C. D.
3.如图,在中,,,,分别是的高线、中线和角平分线,下列结论错误的是( )
A. B.
C. D.
4.如图,在中,点C在的延长线上,点B在上,且,,则的度数为( )
A.60° B.30° C.90° D.80°
5.以下列长度的三条线段为边长,能组成三角形的是( )
A.1,2,4 B.3,4,8 C.5,6,6 D.5,6,11
6.分别用下列长度的三条线段能组成三角形的是( )
A.4,2,1 B.4,4,8 C.4,9,9 D.2,3,6
7.两根木条的长分别是4cm和9cm,要拼成一个三角形,若第三根木条的长度为奇数,则第三根木条的长度的取值情况有( )
A.3种 B.4种 C.5种 D.0种
8.在以下三个图形中,根据尺规作图的痕迹,能判断射线AD平分∠BAC的是( )
A.图1与图2 B.图1与图3
C.图2与图3 D.图1、图2、图3
9.如图,已知,请你在下面四个备选条件:①;②;③;④中任选一个备选条件和已知条件组合,组合后仍然不能证明的备选条件是( )
A.① B.② C.③ D.④
10.如图,把的各边延长2倍至,,,那么的面积是的面积的( )
A.4倍 B.7倍 C.19倍 D.20倍
二、填空题
11.如图,O是直线AB上一点,∠COD是直角,OE平分∠BOC,∠AOC=40°,则∠DOE的度数为 .
12.如图,△ABC中,AC=7,BC=4,AB的垂直平分线DE交AB于点D,交边AC于点E,那么△BCE的周长为 .
13.如图,在中,是延长线上一点,,,则等于 .
14.如图,△ABC≌△DEF,请根据图中提供的信息,写出x= .
15.如图,三点在同一直线上,且.
⑴若,则 ;
⑵当 °时,.
16.容器中有“O、P、Q”三种颗粒,若相同种类的颗粒发生碰撞,则会变成1个“P颗粒;若不同种类的颗粒发生碰撞,则会变成另一种颗粒,例如:一个“O”颗粒和一个“P”颗粒进行碰撞,则会变成一个“Q”颗粒.现有“O”颗粒11个,“P”颗粒10个,“Q”颗粒12个,经过两两碰撞后,最后一个颗粒一定不是 颗粒.
三、计算题
17.(1)已知a、b、c是的三边长,化简:;
(2)已知的三个内角度数之比为1∶1∶2,求这个三角形中最大角的度数.
18. 如图,直线AB//CD,BC平分∠ABD.
(1)若∠ABD=112°,求∠1的度数;
(2)若∠2= x°,求∠ABC的度数(请用含x的代数式表示).
四、解答题
19.如图,BD是△ABC的高线,∠A=60°,∠C=50°.求∠ABD与∠CBD的度数.
20.如图,在△ABC中,∠A=46°,CE是∠ACB的平分线,B,C,D在同一条直线上,DF∥EC,∠D=42°.求∠B的度数.
21.请在方格内画△ABC,使它的顶点都在格点上,且三边长分别为2,2 ,4 ,求①△ABC的面积;②求出最长边上高.
答案解析部分
1.【答案】B
【知识点】角平分线的性质;尺规作图-作角的平分线
2.【答案】C
【知识点】三角形的稳定性
3.【答案】D
【知识点】三角形的角平分线、中线和高;三角形内角和定理
4.【答案】D
【知识点】三角形外角的概念及性质;同位角的概念
5.【答案】C
【知识点】三角形三边关系
6.【答案】C
【知识点】三角形三边关系
7.【答案】A
【知识点】三角形三边关系
8.【答案】B
【知识点】三角形全等的判定-SAS;三角形全等的判定-AAS;尺规作图-作角的平分线
9.【答案】B
【知识点】三角形全等的判定
10.【答案】C
【知识点】三角形的面积
11.【答案】20°
【知识点】余角、补角及其性质;角平分线的性质
12.【答案】11
【知识点】线段垂直平分线的性质
13.【答案】
【知识点】三角形外角的概念及性质
14.【答案】20
【知识点】三角形全等及其性质
15.【答案】4;90
【知识点】平行线的性质;三角形全等及其性质
16.【答案】P
【知识点】推理与论证
17.【答案】(1);(2)这个三角形中最大角的度数为.
【知识点】三角形三边关系;三角形内角和定理;合并同类项法则及应用;化简含绝对值有理数
18.【答案】(1)解:∵BC平分∠ABD,
∴∠ABC=∠ABD=×112°=56°,
∵AB∥CD,
∴∠1=∠ABC=56°
(2)解:∵BC平分∠ABD,
∴∠ABC=∠DBC,
∵AB∥CD,
∴∠1=∠ABC=∠DBC,
∵∠2=∠CDB=180°-∠1-∠DBC=180°-2∠1=x°,
∴
【知识点】三角形内角和定理;角平分线的概念;两直线平行,内错角相等
19.【答案】解:∵BD是三角形ABC的高,
∴BD⊥AC,
∴∠ADB=∠CDB=90°,
又 ∠A=60°,∠C=50°,
∴∠ABD=180°-∠A-∠ADB=30°,∠CBD=180°-∠C-∠CDB=40°.
【知识点】三角形的角平分线、中线和高;三角形内角和定理
20.【答案】解:∵FD∥EC,
∴∠BCE=∠D=42°,
∵CE是∠ACB的平分线,
∴∠ACB=2∠BCE=84°,
∵∠A=46°,
∴∠B=180°-84°-46°=50°.
【知识点】平行线的性质;三角形的角平分线、中线和高;三角形内角和定理
21.【答案】解:①如图∵AC=2,BD=2∴S△ABC= AC×BD=2,②∵最长边AB=2 ,设最长边上的高为h,则S△ABC= AB×h=2,∴h= ,即最长边上高为 .
【知识点】实数在数轴上表示;三角形的面积
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
