第2章 特殊三角形 章末复习(含答案)
文档属性
| 名称 | 第2章 特殊三角形 章末复习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 468.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 19:49:31 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第2章 特殊三角形
一、单选题
1.如图,,,,则能直接判定的理由是( )
A. B. C. D.
2.下列四个说法中,①三个角都相等的三角形是等边三角形,②有两个角等于的三角形是等边三角形,③有一个角是的等腰三角形是等边三角形,④有两个角相等的等腰三角形是等边三角形.正确的有( )个
A.个 B.个 C.个 D.个
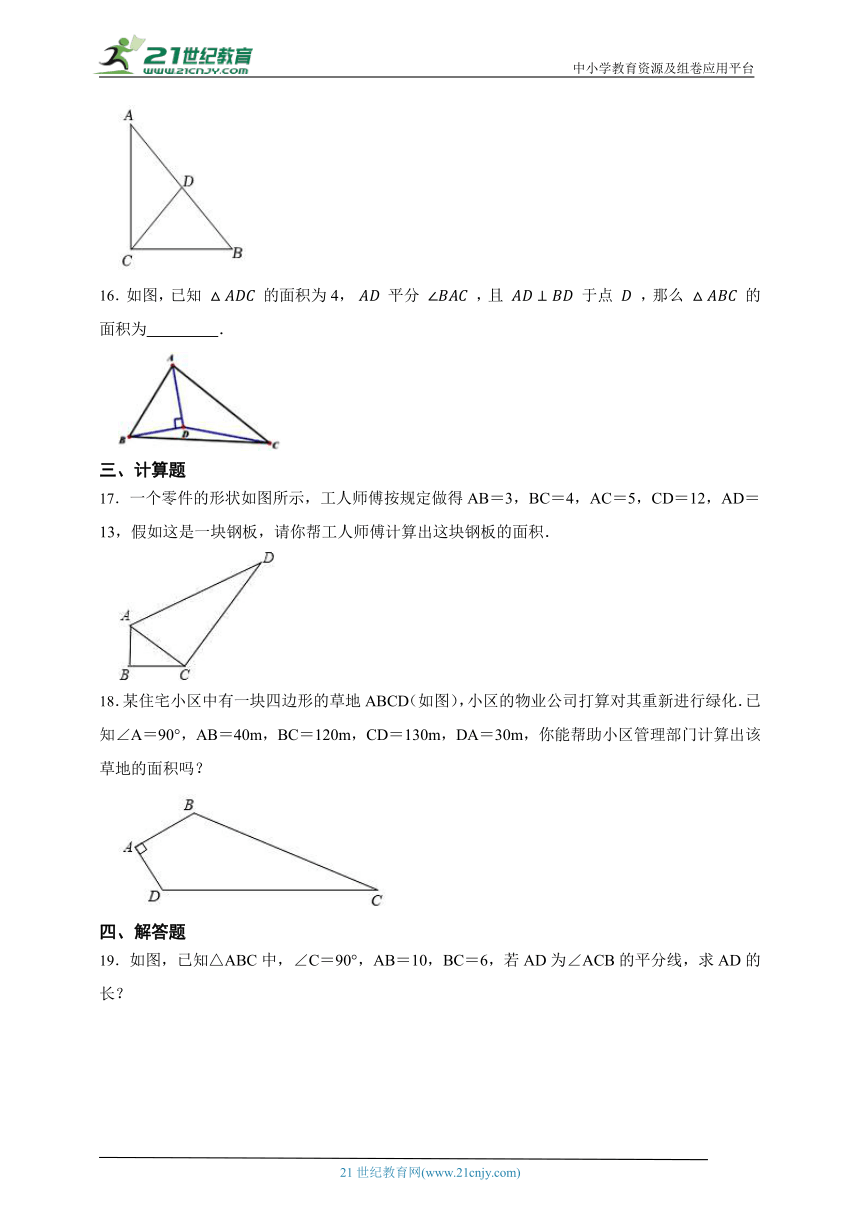
3.一个门框的尺寸如图所示,下列长×宽型号(单位:m)的长方形薄木板能从门框内通过的是( )
A. B. C. D.
4.如图,在中,,是边上的中点,点分别是边上的动点,与相交于点,且.下列个结论:①图中共有对全等三角形;②;③;④.其中正确的结论有( )个.
A.4 B.3 C.2 D.1
5.下列以为三边长的三角形中,是直角三角形的是( )
A. B.
C. D.
6.临汾是帝尧之都,有着尧都之称.尧都华表柱身祥云腾龙,顶蹲冲天吼,底座浮雕长城和黄河壶口瀑布,是中华民族历史悠久、文化灿烂的标志.如图,在底面周长约为6米且带有层层回环不断的云朵石柱上,有一条雕龙从柱底沿立柱表面均匀地盘绕2圈到达柱顶正上方(从点A到点C,B为的中点),每根华表刻有雕龙的部分的柱身高约16米,则雕刻在石柱上的巨龙至少为( )
A.20米 B.25米 C.30米 D.15米
7.如图,在中,的角平分线交于点于点.若,则的周长为( )
A.6 B.12 C.15 D.21
8.如图,在数轴上点A,B所表示得数分别是﹣1,1,CB⊥AB,BC=1,以点A为圆心,AC长为半径画弧,交数轴于点D(点D在点B的右侧),则点D所表示的数是( )
A. B. C. D.2﹣
9.一个直角三角形两条直角边的长分别为6,8,则其斜边上的高为( )
A. B.13 C. D.25
10. 如图所示,AB=AC,∠A=36°,∠1=∠2,且∠ADE 则图中等腰三角形有( )
A.3个 B.4个 C.5个 D.6个
二、填空题
11.如图,是等边三角形的边上的高,,P点是上的动点,Q点是边的中点,则的最小值是 .
12.如图,在直角中,直角边,现要在上找一点D,使得将沿翻折后,点C落在斜边上,则 .
13.如图,点P是外的一点,点M,N分别是两边上的点,点P关于的对称点Q恰好落在线段上,点P关于的对称点R落在的延长线上,若,,,则线段的长为 .
14.已知等腰三角形有一边长为5,一边长为2,则周长为 .
15.如图,在中,,,D为线段AB的中点,则 .
16.如图,已知 的面积为4, 平分 ,且 于点 ,那么 的面积为 .
三、计算题
17.一个零件的形状如图所示,工人师傅按规定做得AB=3,BC=4,AC=5,CD=12,AD=13,假如这是一块钢板,请你帮工人师傅计算出这块钢板的面积.
18.某住宅小区中有一块四边形的草地ABCD(如图),小区的物业公司打算对其重新进行绿化.已知∠A=90°,AB=40m,BC=120m,CD=130m,DA=30m,你能帮助小区管理部门计算出该草地的面积吗?
四、解答题
19.如图,已知△ABC中,∠C=90°,AB=10,BC=6,若AD为∠ACB的平分线,求AD的长?
20.如图,在中,,点是的中点,点在上,,.
(1)求的度数;
(2)求的度数.
21.【再读教材】我们八年级下册数学课本第页介绍了“海伦秦九韶公式”:如果一个三角形的三边长分别为,,,记,那么三角形的面积为.
【解决问题】已知,在中,,,.
(1)请你用“海伦秦九韶公式”求的面积;
(2)除了利用“海伦秦九韶公式”求的面积外,你有其它解法吗?请写出你的解法.
答案解析部分
1.【答案】A
【知识点】直角三角形全等的判定-HL
2.【答案】D
【知识点】等边三角形的判定;等腰三角形的概念
3.【答案】D
【知识点】勾股定理
4.【答案】A
【知识点】三角形外角的概念及性质;三角形全等及其性质;等腰三角形的判定与性质
5.【答案】B
【知识点】三角形三边关系;勾股定理的逆定理
6.【答案】A
【知识点】勾股定理的实际应用-最短路径问题
7.【答案】B
【知识点】直角三角形全等的判定-HL;角平分线的性质
8.【答案】B
【知识点】勾股定理
9.【答案】C
【知识点】三角形的面积;勾股定理
10.【答案】C
【知识点】等腰三角形的判定与性质
11.【答案】8
【知识点】等边三角形的性质;轴对称的性质
12.【答案】3
【知识点】勾股定理
13.【答案】4
【知识点】轴对称的性质
14.【答案】12
【知识点】三角形三边关系;等腰三角形的性质
15.【答案】50°
【知识点】直角三角形斜边上的中线
16.【答案】8
【知识点】三角形的面积;等腰三角形的性质
17.【答案】36
【知识点】勾股定理的逆定理
18.【答案】3600
【知识点】勾股定理;勾股定理的逆定理
19.【答案】
【知识点】角平分线的性质;勾股定理
20.【答案】(1)解:,
∵,
,
,
;
(2)解:点D是的中点,
,
,
∵
.
【知识点】三角形内角和定理;等腰三角形的判定与性质
21.【答案】(1)解:,,,
,
,
即的面积为.
(2)解:,,,
,,,
,
,
.
【知识点】三角形的面积;勾股定理的逆定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第2章 特殊三角形
一、单选题
1.如图,,,,则能直接判定的理由是( )
A. B. C. D.
2.下列四个说法中,①三个角都相等的三角形是等边三角形,②有两个角等于的三角形是等边三角形,③有一个角是的等腰三角形是等边三角形,④有两个角相等的等腰三角形是等边三角形.正确的有( )个
A.个 B.个 C.个 D.个
3.一个门框的尺寸如图所示,下列长×宽型号(单位:m)的长方形薄木板能从门框内通过的是( )
A. B. C. D.
4.如图,在中,,是边上的中点,点分别是边上的动点,与相交于点,且.下列个结论:①图中共有对全等三角形;②;③;④.其中正确的结论有( )个.
A.4 B.3 C.2 D.1
5.下列以为三边长的三角形中,是直角三角形的是( )
A. B.
C. D.
6.临汾是帝尧之都,有着尧都之称.尧都华表柱身祥云腾龙,顶蹲冲天吼,底座浮雕长城和黄河壶口瀑布,是中华民族历史悠久、文化灿烂的标志.如图,在底面周长约为6米且带有层层回环不断的云朵石柱上,有一条雕龙从柱底沿立柱表面均匀地盘绕2圈到达柱顶正上方(从点A到点C,B为的中点),每根华表刻有雕龙的部分的柱身高约16米,则雕刻在石柱上的巨龙至少为( )
A.20米 B.25米 C.30米 D.15米
7.如图,在中,的角平分线交于点于点.若,则的周长为( )
A.6 B.12 C.15 D.21
8.如图,在数轴上点A,B所表示得数分别是﹣1,1,CB⊥AB,BC=1,以点A为圆心,AC长为半径画弧,交数轴于点D(点D在点B的右侧),则点D所表示的数是( )
A. B. C. D.2﹣
9.一个直角三角形两条直角边的长分别为6,8,则其斜边上的高为( )
A. B.13 C. D.25
10. 如图所示,AB=AC,∠A=36°,∠1=∠2,且∠ADE 则图中等腰三角形有( )
A.3个 B.4个 C.5个 D.6个
二、填空题
11.如图,是等边三角形的边上的高,,P点是上的动点,Q点是边的中点,则的最小值是 .
12.如图,在直角中,直角边,现要在上找一点D,使得将沿翻折后,点C落在斜边上,则 .
13.如图,点P是外的一点,点M,N分别是两边上的点,点P关于的对称点Q恰好落在线段上,点P关于的对称点R落在的延长线上,若,,,则线段的长为 .
14.已知等腰三角形有一边长为5,一边长为2,则周长为 .
15.如图,在中,,,D为线段AB的中点,则 .
16.如图,已知 的面积为4, 平分 ,且 于点 ,那么 的面积为 .
三、计算题
17.一个零件的形状如图所示,工人师傅按规定做得AB=3,BC=4,AC=5,CD=12,AD=13,假如这是一块钢板,请你帮工人师傅计算出这块钢板的面积.
18.某住宅小区中有一块四边形的草地ABCD(如图),小区的物业公司打算对其重新进行绿化.已知∠A=90°,AB=40m,BC=120m,CD=130m,DA=30m,你能帮助小区管理部门计算出该草地的面积吗?
四、解答题
19.如图,已知△ABC中,∠C=90°,AB=10,BC=6,若AD为∠ACB的平分线,求AD的长?
20.如图,在中,,点是的中点,点在上,,.
(1)求的度数;
(2)求的度数.
21.【再读教材】我们八年级下册数学课本第页介绍了“海伦秦九韶公式”:如果一个三角形的三边长分别为,,,记,那么三角形的面积为.
【解决问题】已知,在中,,,.
(1)请你用“海伦秦九韶公式”求的面积;
(2)除了利用“海伦秦九韶公式”求的面积外,你有其它解法吗?请写出你的解法.
答案解析部分
1.【答案】A
【知识点】直角三角形全等的判定-HL
2.【答案】D
【知识点】等边三角形的判定;等腰三角形的概念
3.【答案】D
【知识点】勾股定理
4.【答案】A
【知识点】三角形外角的概念及性质;三角形全等及其性质;等腰三角形的判定与性质
5.【答案】B
【知识点】三角形三边关系;勾股定理的逆定理
6.【答案】A
【知识点】勾股定理的实际应用-最短路径问题
7.【答案】B
【知识点】直角三角形全等的判定-HL;角平分线的性质
8.【答案】B
【知识点】勾股定理
9.【答案】C
【知识点】三角形的面积;勾股定理
10.【答案】C
【知识点】等腰三角形的判定与性质
11.【答案】8
【知识点】等边三角形的性质;轴对称的性质
12.【答案】3
【知识点】勾股定理
13.【答案】4
【知识点】轴对称的性质
14.【答案】12
【知识点】三角形三边关系;等腰三角形的性质
15.【答案】50°
【知识点】直角三角形斜边上的中线
16.【答案】8
【知识点】三角形的面积;等腰三角形的性质
17.【答案】36
【知识点】勾股定理的逆定理
18.【答案】3600
【知识点】勾股定理;勾股定理的逆定理
19.【答案】
【知识点】角平分线的性质;勾股定理
20.【答案】(1)解:,
∵,
,
,
;
(2)解:点D是的中点,
,
,
∵
.
【知识点】三角形内角和定理;等腰三角形的判定与性质
21.【答案】(1)解:,,,
,
,
即的面积为.
(2)解:,,,
,,,
,
,
.
【知识点】三角形的面积;勾股定理的逆定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
