1.4全等三角形 同步练习(含答案)
文档属性
| 名称 | 1.4全等三角形 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 487.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 19:31:57 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
1.4 全等三角形
一、单选题
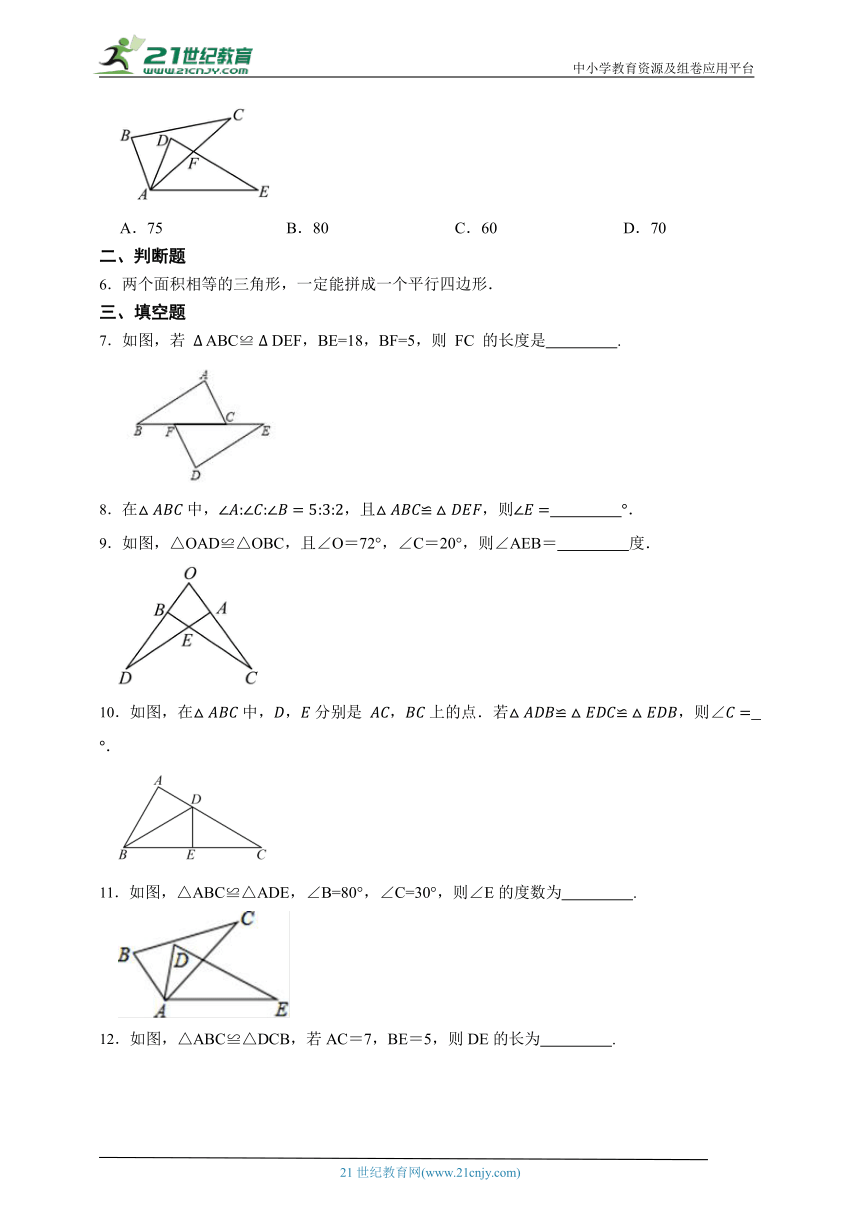
1.如图所示,△ABC≌△DEF,DF和AC,FE和CB是对应边.若∠A=100°,∠F=47°,则∠B的度数是( )
A.33° B.47° C.53° D.100°
2.下列图形中,是全等图形的是( )
A. B.与 C. D.与
3.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )
A.AB=AC B.∠BAE=∠CAD
C.BE=DC D.AD=DE
4.如图,图中的两个三角形全等,则等于( )
A. B. C. D.
5.如图,,若,,,与交于点F,则的度数为( )度
A.75 B.80 C.60 D.70
二、判断题
6.两个面积相等的三角形,一定能拼成一个平行四边形.
三、填空题
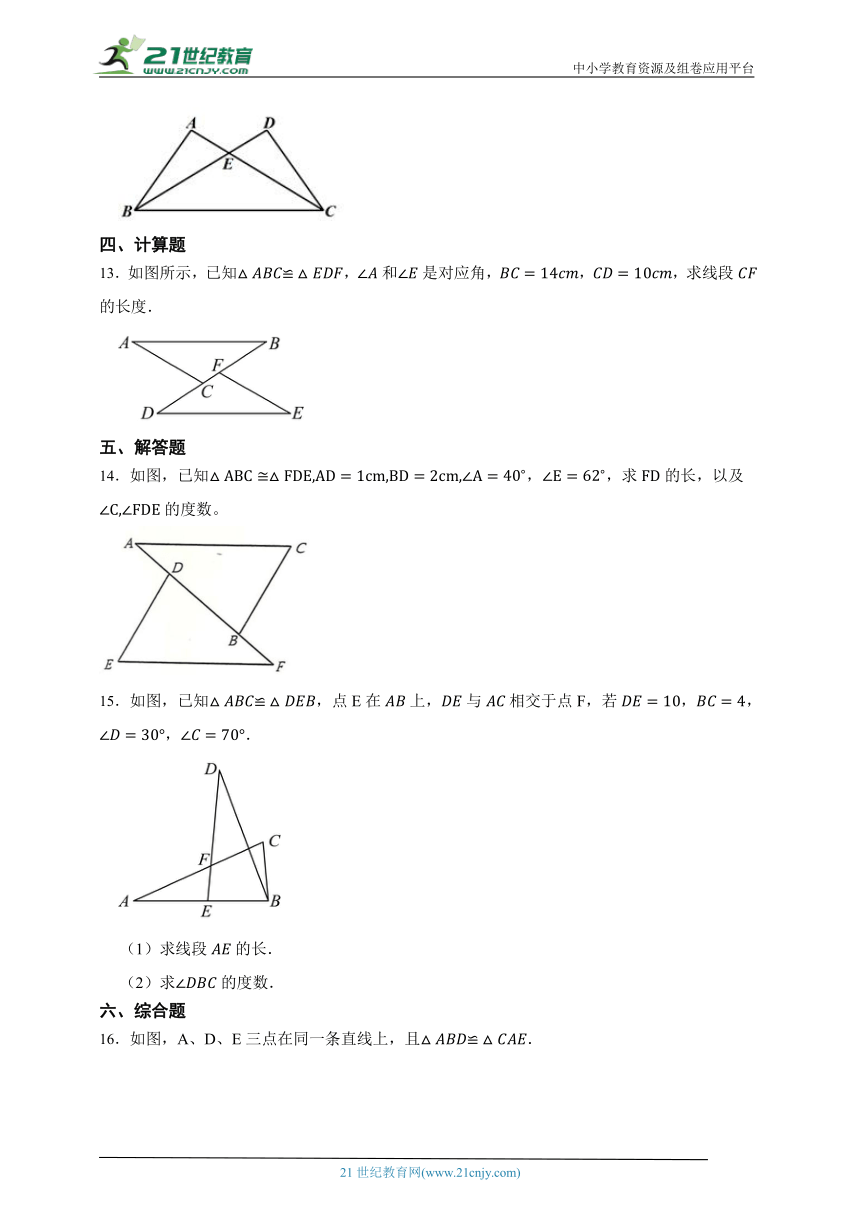
7.如图,若 ABC≌ DEF,BE=18,BF=5,则 FC 的长度是 .
8.在中,,且,则 .
9.如图,△OAD≌△OBC,且∠O=72°,∠C=20°,则∠AEB= 度.
10.如图,在中,,分别是 ,上的点.若,则∠ .
11.如图,△ABC≌△ADE,∠B=80°,∠C=30°,则∠E的度数为 .
12.如图,△ABC≌△DCB,若AC=7,BE=5,则DE的长为 .
四、计算题
13.如图所示,已知,和是对应角,,,求线段的长度.
五、解答题
14.如图,已知,,求的长,以及的度数。
15.如图,已知,点E在上,与相交于点F,若,,,.
(1)求线段的长.
(2)求的度数.
六、综合题
16.如图,A、D、E三点在同一条直线上,且.
(1)若,,求;
(2)若,求.
17.如图,△ABC≌△ADE,其中B与D,C与E对应,
(1)写出对应边和对应角.
(2)∠BAD与∠CAE相等吗?说明理由.
18.如图,已知△ABC≌△EBD,
(1)若BE=6,BD=4,求线段AD的长;
(2)若∠E=30°,∠B=48°,求∠ACE的度数.
答案解析部分
1.【答案】A
【知识点】三角形内角和定理;三角形全等及其性质
2.【答案】D
【知识点】全等图形的概念
3.【答案】D
【知识点】三角形全等及其性质
4.【答案】D
【知识点】三角形内角和定理;三角形全等及其性质
5.【答案】B
【知识点】三角形内角和定理;三角形全等及其性质
6.【答案】错误
【知识点】三角形全等及其性质
7.【答案】8
【知识点】三角形全等及其性质
8.【答案】
【知识点】三角形内角和定理;三角形全等及其性质
9.【答案】112.
【知识点】三角形外角的概念及性质;三角形全等及其性质
10.【答案】
【知识点】三角形内角和定理;三角形全等及其性质
11.【答案】30°
【知识点】三角形全等及其性质
12.【答案】2
【知识点】三角形全等及其性质
13.【答案】
【知识点】三角形全等及其性质
14.【答案】解:∵△ABC≌△FDE,
∴∠C=∠E=62°,∠F=∠A=40°,FD=AB=AD+BD=3(cm),
∴∠FDE=180°-∠E-∠F=180°-62°-40°=78°
【知识点】三角形内角和定理;三角形全等及其性质
15.【答案】(1)
(2)
【知识点】三角形内角和定理;三角形全等及其性质
16.【答案】(1)
(2)
【知识点】三角形全等及其性质;内错角的概念
17.【答案】(1)解:对应边:AB与AD,BC与DE,AC与AE;
对应角:∠BAC与∠DAE,∠B与∠D,∠C与∠E;
(2)解:∠BAD=∠CAE.
理由如下:∵∠BAC=∠DAE,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
即∠BAD=∠CAE.
【知识点】三角形全等及其性质
18.【答案】(1)解:∵△ABC≌△EBD,
∴AB=BE=6,
∵AD=AB-BD,BD=4,
∴AD=6-4=2;
(2)解:∵△ABC≌△EBD,
∴∠A=∠E=30°,
∵∠ACE=∠A+∠B,∠B=48°,
∴∠ACE=30°+48°
=78°.
【知识点】三角形外角的概念及性质;三角形全等及其性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.4 全等三角形
一、单选题
1.如图所示,△ABC≌△DEF,DF和AC,FE和CB是对应边.若∠A=100°,∠F=47°,则∠B的度数是( )
A.33° B.47° C.53° D.100°
2.下列图形中,是全等图形的是( )
A. B.与 C. D.与
3.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )
A.AB=AC B.∠BAE=∠CAD
C.BE=DC D.AD=DE
4.如图,图中的两个三角形全等,则等于( )
A. B. C. D.
5.如图,,若,,,与交于点F,则的度数为( )度
A.75 B.80 C.60 D.70
二、判断题
6.两个面积相等的三角形,一定能拼成一个平行四边形.
三、填空题
7.如图,若 ABC≌ DEF,BE=18,BF=5,则 FC 的长度是 .
8.在中,,且,则 .
9.如图,△OAD≌△OBC,且∠O=72°,∠C=20°,则∠AEB= 度.
10.如图,在中,,分别是 ,上的点.若,则∠ .
11.如图,△ABC≌△ADE,∠B=80°,∠C=30°,则∠E的度数为 .
12.如图,△ABC≌△DCB,若AC=7,BE=5,则DE的长为 .
四、计算题
13.如图所示,已知,和是对应角,,,求线段的长度.
五、解答题
14.如图,已知,,求的长,以及的度数。
15.如图,已知,点E在上,与相交于点F,若,,,.
(1)求线段的长.
(2)求的度数.
六、综合题
16.如图,A、D、E三点在同一条直线上,且.
(1)若,,求;
(2)若,求.
17.如图,△ABC≌△ADE,其中B与D,C与E对应,
(1)写出对应边和对应角.
(2)∠BAD与∠CAE相等吗?说明理由.
18.如图,已知△ABC≌△EBD,
(1)若BE=6,BD=4,求线段AD的长;
(2)若∠E=30°,∠B=48°,求∠ACE的度数.
答案解析部分
1.【答案】A
【知识点】三角形内角和定理;三角形全等及其性质
2.【答案】D
【知识点】全等图形的概念
3.【答案】D
【知识点】三角形全等及其性质
4.【答案】D
【知识点】三角形内角和定理;三角形全等及其性质
5.【答案】B
【知识点】三角形内角和定理;三角形全等及其性质
6.【答案】错误
【知识点】三角形全等及其性质
7.【答案】8
【知识点】三角形全等及其性质
8.【答案】
【知识点】三角形内角和定理;三角形全等及其性质
9.【答案】112.
【知识点】三角形外角的概念及性质;三角形全等及其性质
10.【答案】
【知识点】三角形内角和定理;三角形全等及其性质
11.【答案】30°
【知识点】三角形全等及其性质
12.【答案】2
【知识点】三角形全等及其性质
13.【答案】
【知识点】三角形全等及其性质
14.【答案】解:∵△ABC≌△FDE,
∴∠C=∠E=62°,∠F=∠A=40°,FD=AB=AD+BD=3(cm),
∴∠FDE=180°-∠E-∠F=180°-62°-40°=78°
【知识点】三角形内角和定理;三角形全等及其性质
15.【答案】(1)
(2)
【知识点】三角形内角和定理;三角形全等及其性质
16.【答案】(1)
(2)
【知识点】三角形全等及其性质;内错角的概念
17.【答案】(1)解:对应边:AB与AD,BC与DE,AC与AE;
对应角:∠BAC与∠DAE,∠B与∠D,∠C与∠E;
(2)解:∠BAD=∠CAE.
理由如下:∵∠BAC=∠DAE,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
即∠BAD=∠CAE.
【知识点】三角形全等及其性质
18.【答案】(1)解:∵△ABC≌△EBD,
∴AB=BE=6,
∵AD=AB-BD,BD=4,
∴AD=6-4=2;
(2)解:∵△ABC≌△EBD,
∴∠A=∠E=30°,
∵∠ACE=∠A+∠B,∠B=48°,
∴∠ACE=30°+48°
=78°.
【知识点】三角形外角的概念及性质;三角形全等及其性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
