2.3等腰三角形的性质定理 同步练习(含答案)
文档属性
| 名称 | 2.3等腰三角形的性质定理 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 431.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2.3 等腰三角形的性质定理
一、单选题
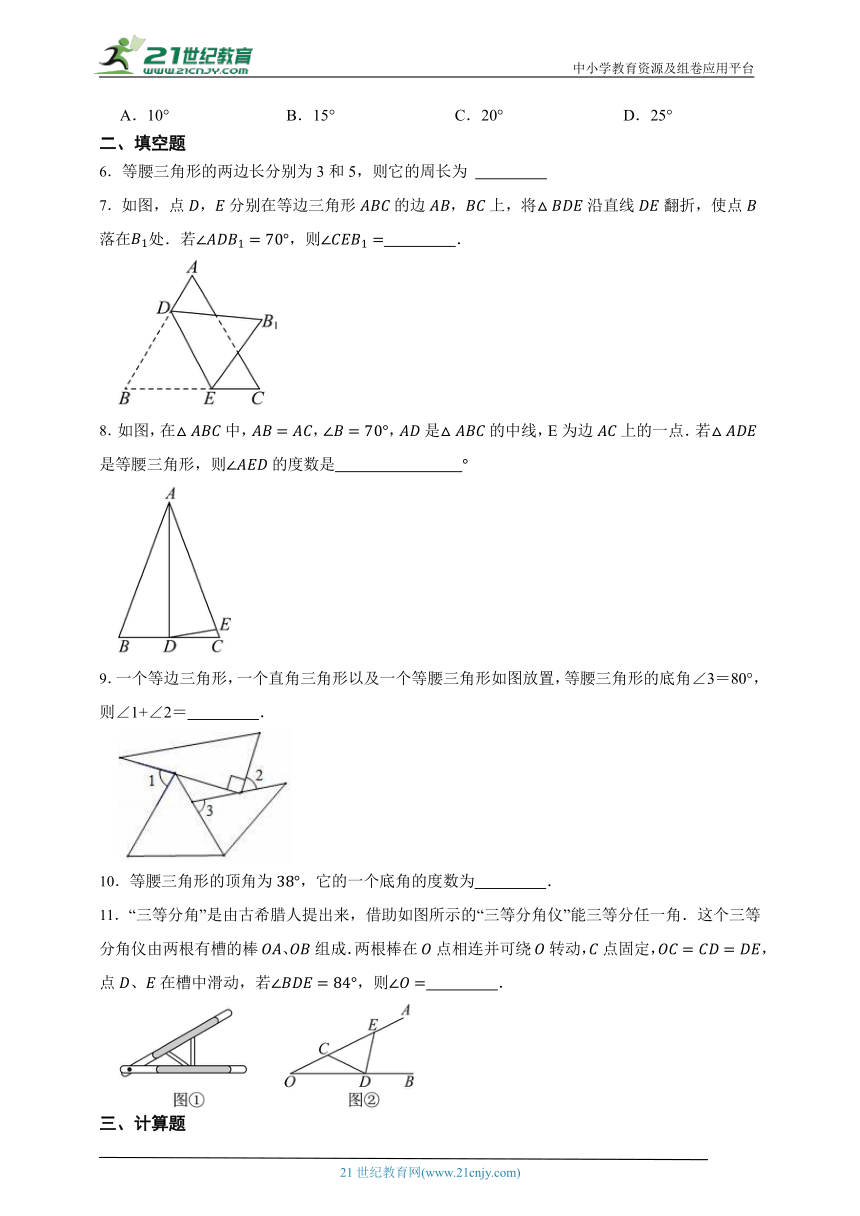
1.已知等边三角形ABC,AB=2,则其周长为( )
A.4 B.5 C.6 D.8
2.如图,A,B两点分别在直线,上,且,,,若,则的度数等于( )
A.30° B.32° C.34° D.36°
3.等腰三角形一边上的高与一腰所夹的锐角是,则该等腰三角形顶角是( )
(1)甲的结果是;(2)乙的结果是;(3)丙的结果是.
A.甲、乙的结果合起来才对
B.乙、丙的结果合起来才对
C.甲、乙、丙的结果合起来才对
D.甲、乙、丙的结果合起来也不对
4.如图,在中,是的平分线,,则的长为( )
A.8 B.7 C.6 D.5
5.如图所示,在等边三角形ABC中,AD⊥BC,E为AD上一点,∠CED=50°,则∠ABE等于( )
A.10° B.15° C.20° D.25°
二、填空题
6.等腰三角形的两边长分别为3和5,则它的周长为
7.如图,点,分别在等边三角形的边,上,将沿直线翻折,使点落在处.若,则 .
8.如图,在中,,,是的中线,E为边上的一点.若是等腰三角形,则的度数是
9.一个等边三角形,一个直角三角形以及一个等腰三角形如图放置,等腰三角形的底角∠3=80°,则∠1+∠2= .
10.等腰三角形的顶角为,它的一个底角的度数为 .
11.“三等分角”是由古希腊人提出来,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒、组成.两根棒在点相连并可绕转动,点固定,,点、在槽中滑动,若,则 .
三、计算题
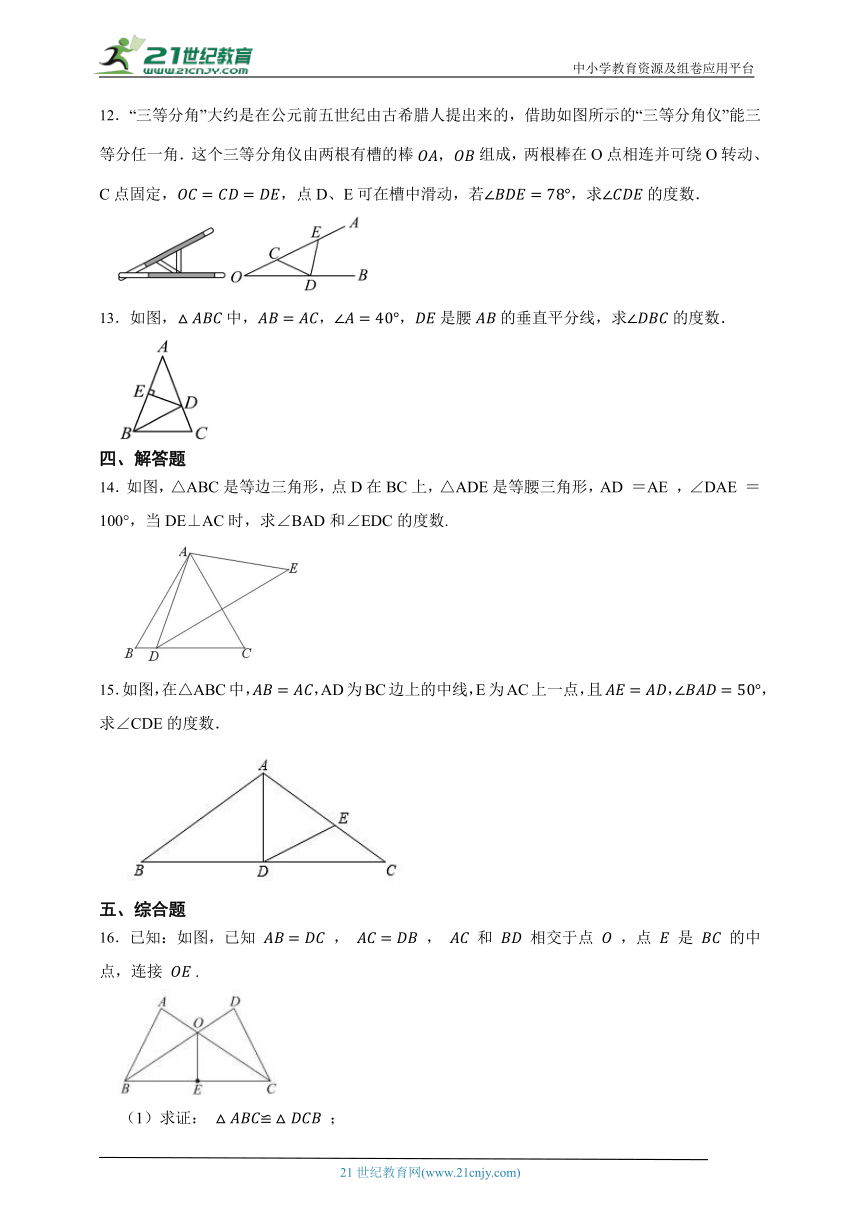
12.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒组成,两根棒在O点相连并可绕O转动、C点固定,,点D、E可在槽中滑动,若,求的度数.
13.如图,中,,,是腰的垂直平分线,求的度数.
四、解答题
14.如图,△ABC是等边三角形,点D在BC上,△ADE是等腰三角形,AD =AE ,∠DAE =100°,当DE⊥AC时,求∠BAD和∠EDC的度数.
15.如图,在△ABC中,,AD为BC边上的中线,E为AC上一点,且,,求∠CDE的度数.
五、综合题
16.已知:如图,已知 , , 和 相交于点 ,点 是 的中点,连接 .
(1)求证: ;
(2)求 的度数.
17.
(1)已知等腰三角形的一边长等于8cm,一边长等于9cm,求它的周长;
(2)等腰三角形的一边长等于6cm,周长等于28cm,求其他两边的长.
18.如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于P.
(1)求证:△ABE≌△CAD;
(2)求∠PBQ的度数.
六、实践探究题
19.【概念学习】
规定①:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“形似三角形”.
规定②:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“形似三角形”,我们把这条线段叫做这个三角形的“等腰分割线”.
(1)【概念理解】
如图1,在△ABC中,∠A=36°,AB=AC,CD平分∠ACB,则△CBD与△ABC (填“是”或“不是”)互为“形似三角形”.
(2)如图2,在△ABC中,CD平分∠ACB,∠A=36°,∠B=48°.求证:CD为△ABC的等腰分割线;
(3)【概念应用】
在△ABC中,∠A=45°,CD是△ABC的等腰分割线,直接写出∠ACB的度数.
答案解析部分
1.【答案】C
【知识点】等边三角形的性质
2.【答案】C
【知识点】三角形内角和定理;等腰三角形的性质;同位角的概念
3.【答案】C
【知识点】等腰三角形的性质;等腰三角形的概念
4.【答案】A
【知识点】三角形外角的概念及性质;等腰三角形的性质
5.【答案】C
【知识点】线段垂直平分线的性质;等边三角形的性质
6.【答案】11或13
【知识点】三角形三边关系;等腰三角形的性质
7.【答案】
【知识点】三角形内角和定理;等边三角形的性质
8.【答案】或
【知识点】三角形内角和定理;等腰三角形的性质
9.【答案】130°
【知识点】角的运算;三角形外角的概念及性质;等边三角形的性质
10.【答案】
【知识点】三角形内角和定理;等腰三角形的性质
11.【答案】
【知识点】三角形外角的概念及性质;等腰三角形的性质
12.【答案】.
【知识点】三角形内角和定理;三角形外角的概念及性质;等腰三角形的性质
13.【答案】
【知识点】三角形内角和定理;线段垂直平分线的性质;等腰三角形的性质
14.【答案】30°
【知识点】三角形外角的概念及性质;等腰三角形的性质;等边三角形的性质
15.【答案】25°
【知识点】三角形内角和定理;等腰三角形的性质
16.【答案】(1)证明:在 和 中,
,
∴
(2)解:∵ ,
∴ ,
∴ .
∵ 是 的中点,
∴ ,
∴
【知识点】等腰三角形的性质;三角形全等的判定-SSS
17.【答案】(1)解:8cm是腰长时,三角形的三边分别为8cm、8cm、9cm,
能组成三角形,周长=8+8+9=25cm,
8cm是底边时,三角形的三边分别为8cm、9cm、9cm,能组成三角形,
周长=8+9+9=26cm,综上所述,周长为25cm或26cm
(2)解:6cm是腰长时,其他两边分别为6cm,16cm,
∵6+6=12<16,
∴不能组成三角形,
6cm是底边时,腰长为 (28-6)=11cm,
三边分别为6cm、11cm、11cm,能组成三角形,
所以,其他两边的长为11cm、11cm
【知识点】三角形三边关系;等腰三角形的性质
18.【答案】(1)证明:∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠C=60°,
在△ABE与△CAD中,
∴△ABE≌△CAD(SAS);
(2)解:由(1)知△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°.
∴∠PBQ=90°-∠BPQ=30°.
【知识点】等边三角形的性质;三角形全等的判定-SAS
19.【答案】(1)是
(2)解:∵∠A=36°,∠B=48°,
∴∠ACB=180°-36°-48°=96°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=∠ACB=48°,
∴∠BCD=∠B=∠ACD,
∴△BCD是等腰三角形,
∴∠ADC=∠BCD+∠B=96°,
在△ABC和△ACD中,
∠A=∠A,∠B=∠ACD,∠ACB=∠ADC,
∴△ABC与△ACD互为“形似三角形”
∴CD为△ABC的等腰分割线.
(3)解:105°或112.5°
【知识点】角的运算;三角形内角和定理;等腰三角形的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.3 等腰三角形的性质定理
一、单选题
1.已知等边三角形ABC,AB=2,则其周长为( )
A.4 B.5 C.6 D.8
2.如图,A,B两点分别在直线,上,且,,,若,则的度数等于( )
A.30° B.32° C.34° D.36°
3.等腰三角形一边上的高与一腰所夹的锐角是,则该等腰三角形顶角是( )
(1)甲的结果是;(2)乙的结果是;(3)丙的结果是.
A.甲、乙的结果合起来才对
B.乙、丙的结果合起来才对
C.甲、乙、丙的结果合起来才对
D.甲、乙、丙的结果合起来也不对
4.如图,在中,是的平分线,,则的长为( )
A.8 B.7 C.6 D.5
5.如图所示,在等边三角形ABC中,AD⊥BC,E为AD上一点,∠CED=50°,则∠ABE等于( )
A.10° B.15° C.20° D.25°
二、填空题
6.等腰三角形的两边长分别为3和5,则它的周长为
7.如图,点,分别在等边三角形的边,上,将沿直线翻折,使点落在处.若,则 .
8.如图,在中,,,是的中线,E为边上的一点.若是等腰三角形,则的度数是
9.一个等边三角形,一个直角三角形以及一个等腰三角形如图放置,等腰三角形的底角∠3=80°,则∠1+∠2= .
10.等腰三角形的顶角为,它的一个底角的度数为 .
11.“三等分角”是由古希腊人提出来,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒、组成.两根棒在点相连并可绕转动,点固定,,点、在槽中滑动,若,则 .
三、计算题
12.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒组成,两根棒在O点相连并可绕O转动、C点固定,,点D、E可在槽中滑动,若,求的度数.
13.如图,中,,,是腰的垂直平分线,求的度数.
四、解答题
14.如图,△ABC是等边三角形,点D在BC上,△ADE是等腰三角形,AD =AE ,∠DAE =100°,当DE⊥AC时,求∠BAD和∠EDC的度数.
15.如图,在△ABC中,,AD为BC边上的中线,E为AC上一点,且,,求∠CDE的度数.
五、综合题
16.已知:如图,已知 , , 和 相交于点 ,点 是 的中点,连接 .
(1)求证: ;
(2)求 的度数.
17.
(1)已知等腰三角形的一边长等于8cm,一边长等于9cm,求它的周长;
(2)等腰三角形的一边长等于6cm,周长等于28cm,求其他两边的长.
18.如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于P.
(1)求证:△ABE≌△CAD;
(2)求∠PBQ的度数.
六、实践探究题
19.【概念学习】
规定①:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“形似三角形”.
规定②:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“形似三角形”,我们把这条线段叫做这个三角形的“等腰分割线”.
(1)【概念理解】
如图1,在△ABC中,∠A=36°,AB=AC,CD平分∠ACB,则△CBD与△ABC (填“是”或“不是”)互为“形似三角形”.
(2)如图2,在△ABC中,CD平分∠ACB,∠A=36°,∠B=48°.求证:CD为△ABC的等腰分割线;
(3)【概念应用】
在△ABC中,∠A=45°,CD是△ABC的等腰分割线,直接写出∠ACB的度数.
答案解析部分
1.【答案】C
【知识点】等边三角形的性质
2.【答案】C
【知识点】三角形内角和定理;等腰三角形的性质;同位角的概念
3.【答案】C
【知识点】等腰三角形的性质;等腰三角形的概念
4.【答案】A
【知识点】三角形外角的概念及性质;等腰三角形的性质
5.【答案】C
【知识点】线段垂直平分线的性质;等边三角形的性质
6.【答案】11或13
【知识点】三角形三边关系;等腰三角形的性质
7.【答案】
【知识点】三角形内角和定理;等边三角形的性质
8.【答案】或
【知识点】三角形内角和定理;等腰三角形的性质
9.【答案】130°
【知识点】角的运算;三角形外角的概念及性质;等边三角形的性质
10.【答案】
【知识点】三角形内角和定理;等腰三角形的性质
11.【答案】
【知识点】三角形外角的概念及性质;等腰三角形的性质
12.【答案】.
【知识点】三角形内角和定理;三角形外角的概念及性质;等腰三角形的性质
13.【答案】
【知识点】三角形内角和定理;线段垂直平分线的性质;等腰三角形的性质
14.【答案】30°
【知识点】三角形外角的概念及性质;等腰三角形的性质;等边三角形的性质
15.【答案】25°
【知识点】三角形内角和定理;等腰三角形的性质
16.【答案】(1)证明:在 和 中,
,
∴
(2)解:∵ ,
∴ ,
∴ .
∵ 是 的中点,
∴ ,
∴
【知识点】等腰三角形的性质;三角形全等的判定-SSS
17.【答案】(1)解:8cm是腰长时,三角形的三边分别为8cm、8cm、9cm,
能组成三角形,周长=8+8+9=25cm,
8cm是底边时,三角形的三边分别为8cm、9cm、9cm,能组成三角形,
周长=8+9+9=26cm,综上所述,周长为25cm或26cm
(2)解:6cm是腰长时,其他两边分别为6cm,16cm,
∵6+6=12<16,
∴不能组成三角形,
6cm是底边时,腰长为 (28-6)=11cm,
三边分别为6cm、11cm、11cm,能组成三角形,
所以,其他两边的长为11cm、11cm
【知识点】三角形三边关系;等腰三角形的性质
18.【答案】(1)证明:∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠C=60°,
在△ABE与△CAD中,
∴△ABE≌△CAD(SAS);
(2)解:由(1)知△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°.
∴∠PBQ=90°-∠BPQ=30°.
【知识点】等边三角形的性质;三角形全等的判定-SAS
19.【答案】(1)是
(2)解:∵∠A=36°,∠B=48°,
∴∠ACB=180°-36°-48°=96°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=∠ACB=48°,
∴∠BCD=∠B=∠ACD,
∴△BCD是等腰三角形,
∴∠ADC=∠BCD+∠B=96°,
在△ABC和△ACD中,
∠A=∠A,∠B=∠ACD,∠ACB=∠ADC,
∴△ABC与△ACD互为“形似三角形”
∴CD为△ABC的等腰分割线.
(3)解:105°或112.5°
【知识点】角的运算;三角形内角和定理;等腰三角形的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
