2.1 直线与圆的位置关系 课件(共20张PPT) 浙教版数学九年级下册
文档属性
| 名称 | 2.1 直线与圆的位置关系 课件(共20张PPT) 浙教版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 30.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 17:14:06 | ||
图片预览


文档简介
(共20张PPT)
浙教版初中数学九年级下册
2.1 直线与圆的位置关系
情境
思考:在图中你能看到哪些学过的几何图形?
小鸟
栖息在线上
太阳
呼唤着它的小名
美好的故事即将开始……
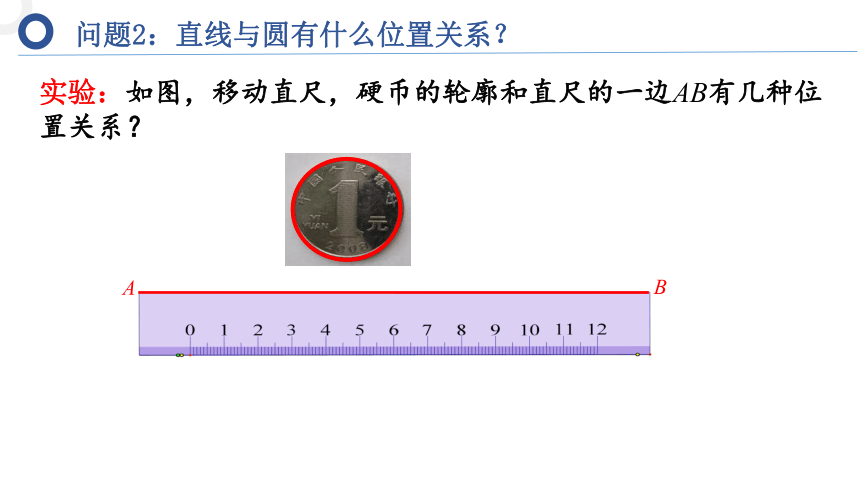
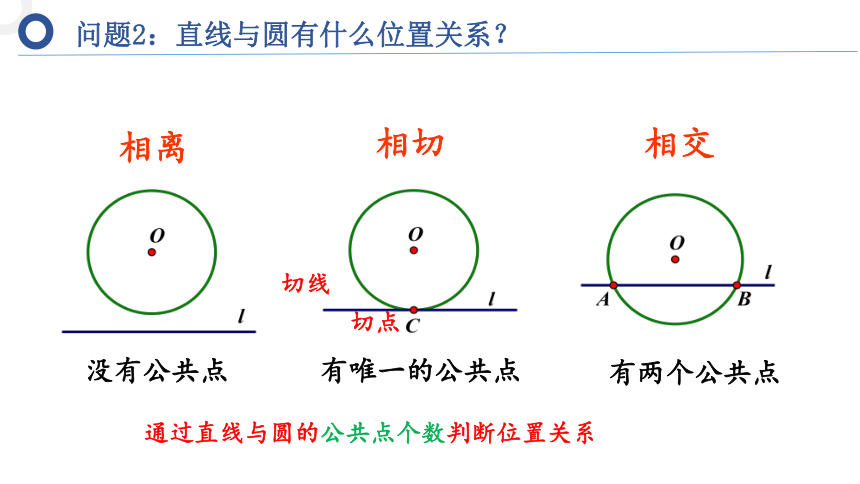
问题2:直线与圆有什么位置关系?
实验:如图,移动直尺,硬币的轮廓和直尺的一边AB有几种位置关系?
A
B
没有公共点
有唯一的公共点
相交
有两个公共点
切点
相切
切线
相离
问题2:直线与圆有什么位置关系?
通过直线与圆的公共点个数判断位置关系
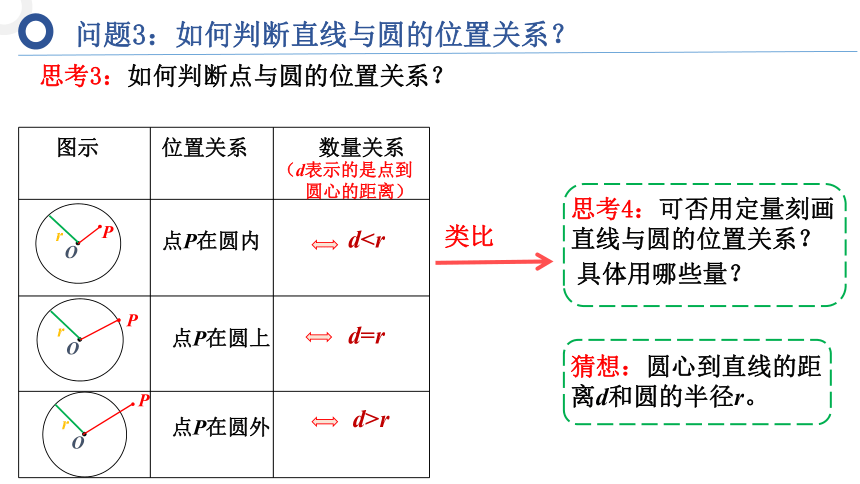
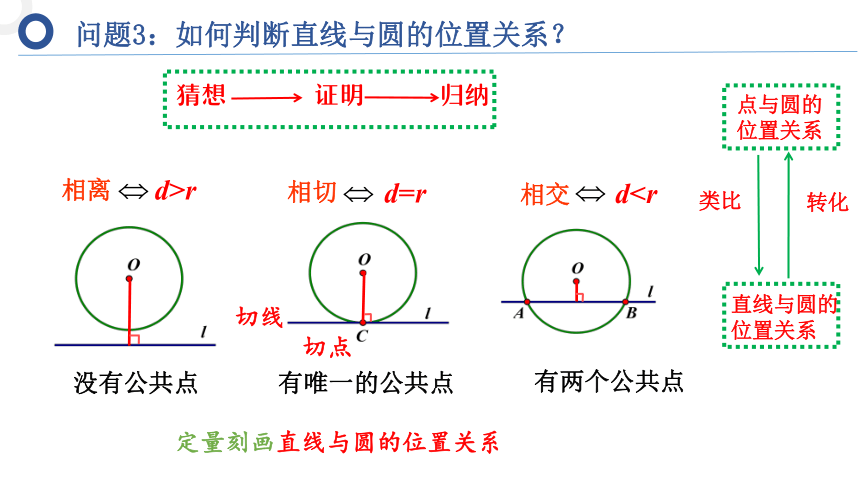
问题3:如何判断直线与圆的位置关系?
思考3:如何判断点与圆的位置关系?
O
r
P
O
r
P
O
r
P
图示
位置关系
点P在圆内
点P在圆上
点P在圆外
d>r
d=r
d数量关系
类比
思考4:可否用定量刻画直线与圆的位置关系?
猜想:圆心到直线的距离d和圆的半径r。
具体用哪些量?
(d表示的是点到
圆心的距离)
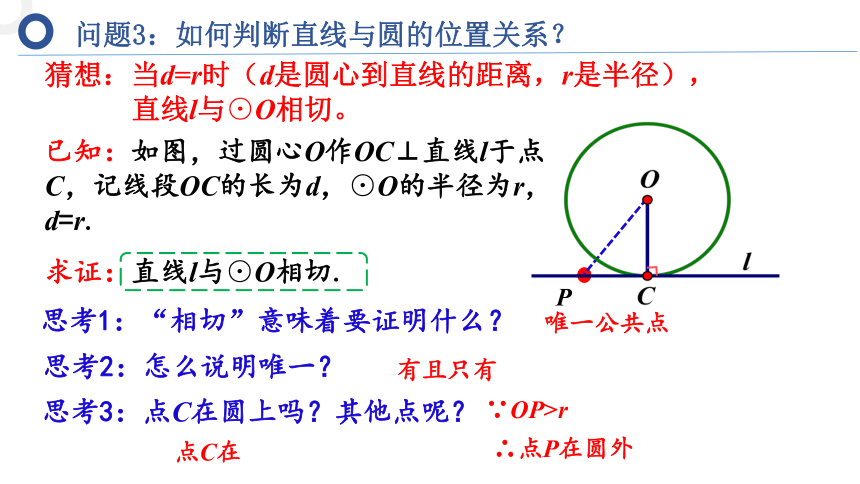
已知:如图,过圆心O作OC⊥直线l于点C,记线段OC的长为d,⊙O的半径为r,d=r.
求证:直线l与⊙O相切.
思考3:点C在圆上吗?其他点呢?
思考1:“相切”意味着要证明什么?
思考2:怎么说明唯一?
P
唯一公共点
猜想:当d=r时(d是圆心到直线的距离,r是半径),
直线l与⊙O相切。
∵OP>r
∴点P在圆外
问题3:如何判断直线与圆的位置关系?
点C在
有且只有
没有公共点
有唯一的公共点
相交
有两个公共点
切点
相切
切线
相离
定量刻画直线与圆的位置关系
d>r
d=r
d猜想 证明 归纳
问题3:如何判断直线与圆的位置关系?
点与圆的
位置关系
转化
直线与圆的位置关系
类比
问题3:如何判断直线与圆的位置关系?
没有公共点
相离
图示
有唯一公共点
有两个公共点
位置关系
相切
相交
数量关系
d>r
d=r
d(d表示的是圆心到直线的距离)
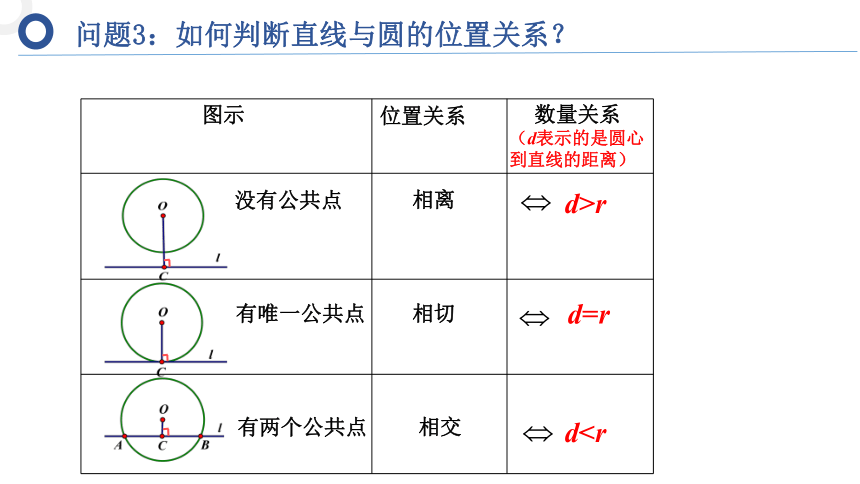
问题3:如何判断直线与圆的位置关系?
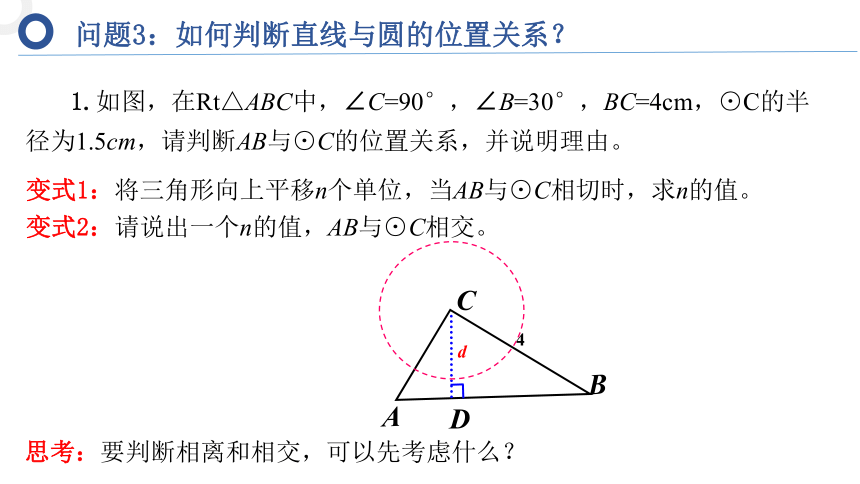
1.如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=4cm,⊙C的半径为1.5cm,请判断AB与⊙C的位置关系,并说明理由。
B
C
A
4
D
d
变式1:将三角形向上平移n个单位,当AB与⊙C相切时,求n的值。
变式2:请说出一个n的值,AB与⊙C相交。
思考:要判断相离和相交,可以先考虑什么?
问题2:如何判断直线与圆的位置关系?
例1 已知:如图,P为∠ABC的角平分线上一点,⊙P与BC相切,求证:⊙P与AB相切.
角平分线上的点到
角两边的距离相等
d1
d2
d1=r
d2=r
d1=d2
思考:如何说明直线与圆相切?
例2 在码头A的北偏东60°方向有一个海岛,离该岛中心P的8海里范围内是一个暗礁区。货船从码头A由西向东方向航行,行驶了10海里到达B,这时岛中心P在北偏东30°方向。若货船不改变航向,问货船会不会进入暗礁区?
北
H
P
A
B
60°
30°
暗礁区
问题3:如何判断直线与圆的位置关系?
任务:根据题意画出示意图,分析思路。
要求:先独立思考,再小组合作。
生活中的问题 数学问题
转化
问题4:本节课你学到了什么?
(1)本节课学了什么?怎么研究的?
(2)在方法上,你有何收获?
(3)接下来会学什么呢?
直线与圆的位置关系
点与圆的位置关系
转化
类比
实验
证明
猜想
圆与圆的
位置关系
作业
(1)基础题:作业本A组
(2)拓展题:作业本B组
问题4:本节课你学到了什么?
图形之间的位置关系
定性描述
定量刻画
研究过程:
思想方法:类比思想,转化思想,分类讨论思想
问题4:本节课你学到了什么?
几何图形的位置关系
分类 位置关系 量化判定方法
点与点 重合 非重合
点与直线 点在直线上 点在直线外
点与圆 点在圆内 点在圆上 点在圆外
直线与直线 平行 相交
直线与圆 相离 相切 相交
圆与圆
点与点之间的距离
点与直线之间的距离
点的坐标与直线解析式
点到圆心的距离与圆的半径之间的关系
同位角(或内错角或同旁内角)之间的数量关系
圆心到直线的距离与圆的半径之间的关系
?
?
(没有公共点)
(2个公共点)
?
思考1:下图中直线与圆有什么位置关系?
思考2:有没有其他方法可以刻画直线与圆的位置关系?
相离
相交
(2个公共点)
相交
问题3:如何判断直线与圆的位置关系?
已知:如图,过圆心O作OC⊥直线l于点C,记线段OC的长为d,⊙O的半径为r,d=r.
求证:直线l与⊙O相切.
P
命题:当d=r时(d是圆心到直线的距离,r是半径),
直线l与⊙O相切。
∵OP>r
问题3:如何判断直线与圆的位置关系?
∴点C(垂足)在圆上
∴P在圆外
N
T
思考1:“相切”意味着要证明什么?
有且只有一个公共点
分析法
∵d=r
问题3:如何判断直线与圆的位置关系?
例1 已知:如图,P为∠ABC的角平分线上一点,⊙P与BC相切,求证:⊙P与AB相切.
问题3:如何判断直线与圆的位置关系?
1.设⊙O的半径为r,圆心O到直线l的距离为d。
根据下列条件判断直线l与⊙O的位置关系。
(1)d=4,r=3;
(2)d= ,r= ;
(3)d=2,r=2。
∵d>r
∴直线l与⊙O相离。
∵d∴直线l与⊙O相交。
∴直线l与⊙O相切。
∵d=r
问题3:如何判断直线与圆的位置关系?
1.设⊙O的半径为r,圆心O到直线l的距离为d。
根据下列条件判断直线l与⊙O的位置关系。
(1)d=4,r=3;
(2)d= ,r= ;
(3)d=2,r=2。
∵d>r
∴直线l与⊙O相离。
∵d∴直线l与⊙O相交。
∴直线l与⊙O相切。
∵d=r
浙教版初中数学九年级下册
2.1 直线与圆的位置关系
情境
思考:在图中你能看到哪些学过的几何图形?
小鸟
栖息在线上
太阳
呼唤着它的小名
美好的故事即将开始……
问题2:直线与圆有什么位置关系?
实验:如图,移动直尺,硬币的轮廓和直尺的一边AB有几种位置关系?
A
B
没有公共点
有唯一的公共点
相交
有两个公共点
切点
相切
切线
相离
问题2:直线与圆有什么位置关系?
通过直线与圆的公共点个数判断位置关系
问题3:如何判断直线与圆的位置关系?
思考3:如何判断点与圆的位置关系?
O
r
P
O
r
P
O
r
P
图示
位置关系
点P在圆内
点P在圆上
点P在圆外
d>r
d=r
d
类比
思考4:可否用定量刻画直线与圆的位置关系?
猜想:圆心到直线的距离d和圆的半径r。
具体用哪些量?
(d表示的是点到
圆心的距离)
已知:如图,过圆心O作OC⊥直线l于点C,记线段OC的长为d,⊙O的半径为r,d=r.
求证:直线l与⊙O相切.
思考3:点C在圆上吗?其他点呢?
思考1:“相切”意味着要证明什么?
思考2:怎么说明唯一?
P
唯一公共点
猜想:当d=r时(d是圆心到直线的距离,r是半径),
直线l与⊙O相切。
∵OP>r
∴点P在圆外
问题3:如何判断直线与圆的位置关系?
点C在
有且只有
没有公共点
有唯一的公共点
相交
有两个公共点
切点
相切
切线
相离
定量刻画直线与圆的位置关系
d>r
d=r
d
问题3:如何判断直线与圆的位置关系?
点与圆的
位置关系
转化
直线与圆的位置关系
类比
问题3:如何判断直线与圆的位置关系?
没有公共点
相离
图示
有唯一公共点
有两个公共点
位置关系
相切
相交
数量关系
d>r
d=r
d
问题3:如何判断直线与圆的位置关系?
1.如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=4cm,⊙C的半径为1.5cm,请判断AB与⊙C的位置关系,并说明理由。
B
C
A
4
D
d
变式1:将三角形向上平移n个单位,当AB与⊙C相切时,求n的值。
变式2:请说出一个n的值,AB与⊙C相交。
思考:要判断相离和相交,可以先考虑什么?
问题2:如何判断直线与圆的位置关系?
例1 已知:如图,P为∠ABC的角平分线上一点,⊙P与BC相切,求证:⊙P与AB相切.
角平分线上的点到
角两边的距离相等
d1
d2
d1=r
d2=r
d1=d2
思考:如何说明直线与圆相切?
例2 在码头A的北偏东60°方向有一个海岛,离该岛中心P的8海里范围内是一个暗礁区。货船从码头A由西向东方向航行,行驶了10海里到达B,这时岛中心P在北偏东30°方向。若货船不改变航向,问货船会不会进入暗礁区?
北
H
P
A
B
60°
30°
暗礁区
问题3:如何判断直线与圆的位置关系?
任务:根据题意画出示意图,分析思路。
要求:先独立思考,再小组合作。
生活中的问题 数学问题
转化
问题4:本节课你学到了什么?
(1)本节课学了什么?怎么研究的?
(2)在方法上,你有何收获?
(3)接下来会学什么呢?
直线与圆的位置关系
点与圆的位置关系
转化
类比
实验
证明
猜想
圆与圆的
位置关系
作业
(1)基础题:作业本A组
(2)拓展题:作业本B组
问题4:本节课你学到了什么?
图形之间的位置关系
定性描述
定量刻画
研究过程:
思想方法:类比思想,转化思想,分类讨论思想
问题4:本节课你学到了什么?
几何图形的位置关系
分类 位置关系 量化判定方法
点与点 重合 非重合
点与直线 点在直线上 点在直线外
点与圆 点在圆内 点在圆上 点在圆外
直线与直线 平行 相交
直线与圆 相离 相切 相交
圆与圆
点与点之间的距离
点与直线之间的距离
点的坐标与直线解析式
点到圆心的距离与圆的半径之间的关系
同位角(或内错角或同旁内角)之间的数量关系
圆心到直线的距离与圆的半径之间的关系
?
?
(没有公共点)
(2个公共点)
?
思考1:下图中直线与圆有什么位置关系?
思考2:有没有其他方法可以刻画直线与圆的位置关系?
相离
相交
(2个公共点)
相交
问题3:如何判断直线与圆的位置关系?
已知:如图,过圆心O作OC⊥直线l于点C,记线段OC的长为d,⊙O的半径为r,d=r.
求证:直线l与⊙O相切.
P
命题:当d=r时(d是圆心到直线的距离,r是半径),
直线l与⊙O相切。
∵OP>r
问题3:如何判断直线与圆的位置关系?
∴点C(垂足)在圆上
∴P在圆外
N
T
思考1:“相切”意味着要证明什么?
有且只有一个公共点
分析法
∵d=r
问题3:如何判断直线与圆的位置关系?
例1 已知:如图,P为∠ABC的角平分线上一点,⊙P与BC相切,求证:⊙P与AB相切.
问题3:如何判断直线与圆的位置关系?
1.设⊙O的半径为r,圆心O到直线l的距离为d。
根据下列条件判断直线l与⊙O的位置关系。
(1)d=4,r=3;
(2)d= ,r= ;
(3)d=2,r=2。
∵d>r
∴直线l与⊙O相离。
∵d
∴直线l与⊙O相切。
∵d=r
问题3:如何判断直线与圆的位置关系?
1.设⊙O的半径为r,圆心O到直线l的距离为d。
根据下列条件判断直线l与⊙O的位置关系。
(1)d=4,r=3;
(2)d= ,r= ;
(3)d=2,r=2。
∵d>r
∴直线l与⊙O相离。
∵d
∴直线l与⊙O相切。
∵d=r
