1.3 绝对值 课件(共14张PPT) 浙教版(2024)数学七年级上册
文档属性
| 名称 | 1.3 绝对值 课件(共14张PPT) 浙教版(2024)数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 548.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-25 00:00:00 | ||
图片预览



文档简介
(共14张PPT)
1.3 绝对值
学习目标
1.借助数轴理解绝对值的意义,体会数形结合的思想方法。
2.掌握求有理数的绝对值的方法。
3.掌握绝对值的性质。
4.会利用绝对值解决简单的问题,培养应用意识。
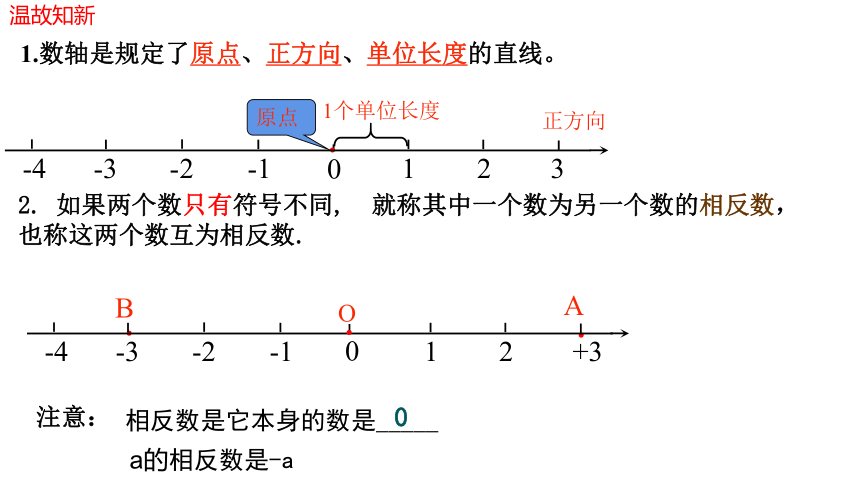
1.数轴是规定了原点、正方向、单位长度的直线。
B
A
-4
-3
-2
-1
+3
2
1
0
O
0
-4
-3
-2
-1
3
2
1
1个单位长度
原点
正方向
2. 如果两个数只有符号不同, 就称其中一个数为另一个数的相反数, 也称这两个数互为相反数.
温故知新
注意:
相反数是它本身的数是_____
0
a的相反数是-a
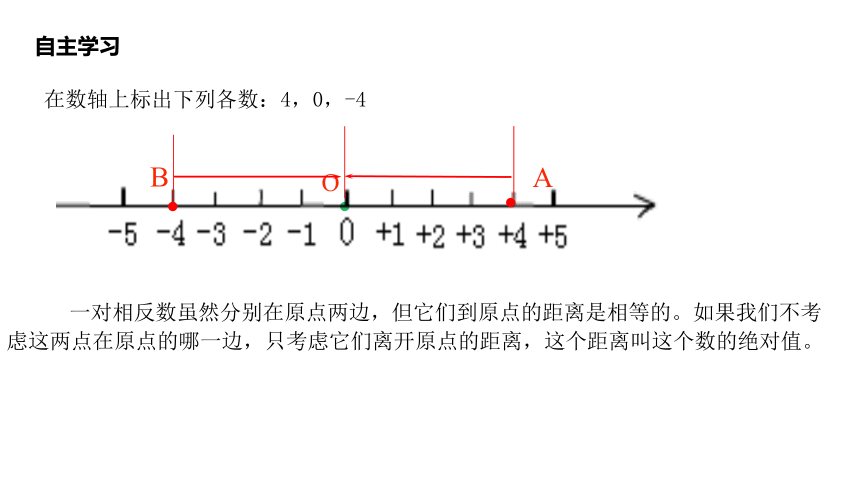
在数轴上标出下列各数:4,0,-4
.
.
.
一对相反数虽然分别在原点两边,但它们到原点的距离是相等的。如果我们不考虑这两点在原点的哪一边,只考虑它们离开原点的距离,这个距离叫这个数的绝对值。
A
O
B
自主学习
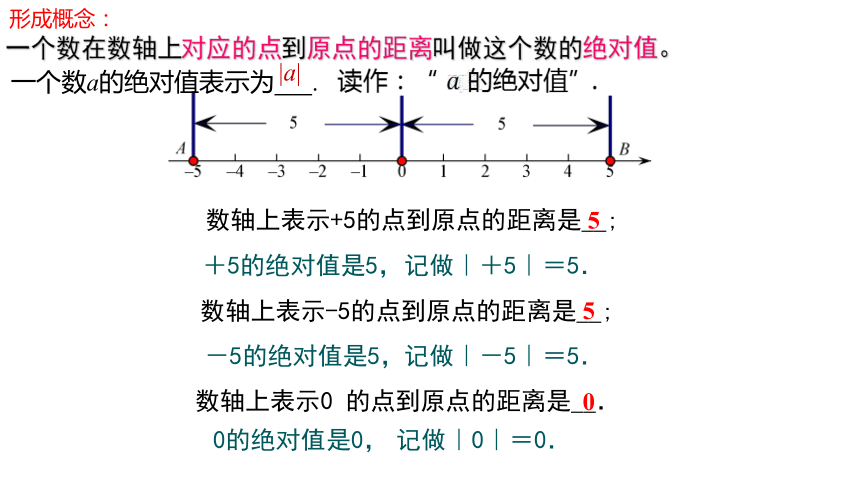
数轴上表示+5的点到原点的距离是__;
数轴上表示-5的点到原点的距离是__;
数轴上表示0 的点到原点的距离是__.
+5的绝对值是5,
记做|+5|=5.
-5的绝对值是5,
记做|-5|=5.
0的绝对值是0,
记做|0|=0.
5
5
0
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值。
一个数a的绝对值表示为 .
|a|
形成概念:
读作:“
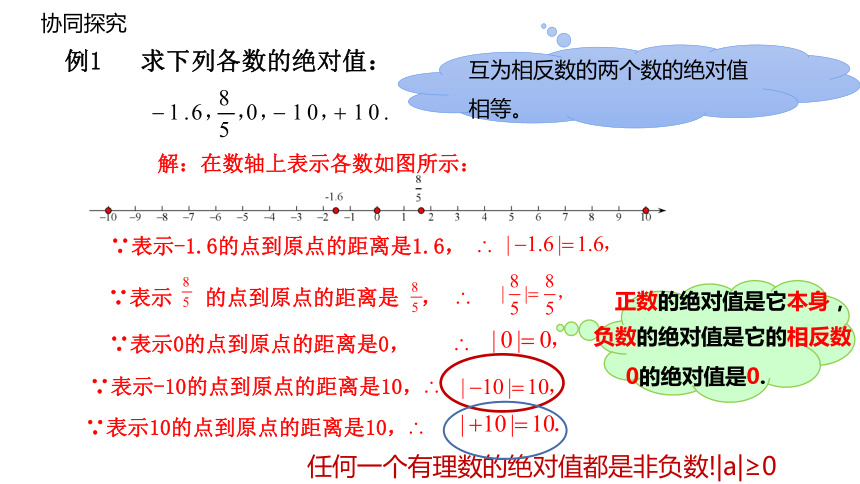
解:在数轴上表示各数如图所示:
∵表示-1.6的点到原点的距离是1.6, ∴
∵表示 的点到原点的距离是 , ∴
∵表示0的点到原点的距离是0, ∴
∵表示-10的点到原点的距离是10,∴
∵表示10的点到原点的距离是10,∴
例1 求下列各数的绝对值:
0的绝对值是0.
协同探究
正数的绝对值是它本身,
负数的绝对值是它的相反数
任何一个有理数的绝对值都是非负数!|a|≥0
互为相反数的两个数的绝对值相等。
知识过关
①一个数在数轴上对应的点到原点的 距离 叫作这个数的绝对值.
②一个正数的绝对值是 它本身 ;一个负数的绝对值是 它的相反数 ;0的绝对值是 0 .
③互为相反数的两个数的绝对值 相等 .
检测评价
距离
它本身
它的相反数
0
相等
考点一: 绝对值的概念
1. -2025的绝对值是( A )
2.已知有理数a,b,c满足|a|>|b|>|c|,这三个数在数轴上对应的点的位置可能是( A )
考点二: 绝对值的性质
[2023·台州](1)已知|a|=|-2|,则a等于( D )
(2)下列说法不正确的是( C )
A. 任意一个有理数的绝对值不一定是正数
B. 负数的绝对值是它的相反数
C. 如果两个数的绝对值相等,那么这两个数相等
D. 0的绝对值是0
考点二: 绝对值的性质
[2024·衢州模拟]用符号语言表述“负数的绝对值等于它的相反数”正确的是( D )
A. |-a|=a
B. |a|=-a
C. |-a|=a(a<0)
D. |a|=-a(a<0)
|x-4|+|y+6|=0,求x+y的值
考点三: 与绝对值有关的计算
已知a=-2,b=1,则|a|+|-b|的值为( A )
A. 3 B. 1 C. 0 D. -1
[教材母题]计算:|-7|+ - ;
考点四: 情境题·生活应用
某出租车司机一日从公司出发,在东西方向的人民路上连续接送5批客人,行驶路程记录如下(规定向东为正,向西为负,单位:km):
第1批 第2批 第3批 第4批 第5批
5 2 -4 -3 10
若该出租车每千米耗油0.08升,那么在这个过程中共耗油多少升?
考点五: 新考法·阅读类比法
同学们都知道,|7-(-1)|表示7与-1之差的绝对值,实际上也可以理解为7与-1两数在数轴上所对应的两点之间的距离.如|x-6|的几何意义是数轴上表示数x的点与表示数6的点之间的距离.试探索:
(1)求|3-(-2)|= ;若|x-(-2)|=3,
则x= ;
(2)|x-1|+|x-(-3)|的最小值是 ;
(3)求当x为何值时,|x-(-1)|+|x-2|+|x-4|的值最小,最小值多少?
课堂总结
1.3 绝对值
学习目标
1.借助数轴理解绝对值的意义,体会数形结合的思想方法。
2.掌握求有理数的绝对值的方法。
3.掌握绝对值的性质。
4.会利用绝对值解决简单的问题,培养应用意识。
1.数轴是规定了原点、正方向、单位长度的直线。
B
A
-4
-3
-2
-1
+3
2
1
0
O
0
-4
-3
-2
-1
3
2
1
1个单位长度
原点
正方向
2. 如果两个数只有符号不同, 就称其中一个数为另一个数的相反数, 也称这两个数互为相反数.
温故知新
注意:
相反数是它本身的数是_____
0
a的相反数是-a
在数轴上标出下列各数:4,0,-4
.
.
.
一对相反数虽然分别在原点两边,但它们到原点的距离是相等的。如果我们不考虑这两点在原点的哪一边,只考虑它们离开原点的距离,这个距离叫这个数的绝对值。
A
O
B
自主学习
数轴上表示+5的点到原点的距离是__;
数轴上表示-5的点到原点的距离是__;
数轴上表示0 的点到原点的距离是__.
+5的绝对值是5,
记做|+5|=5.
-5的绝对值是5,
记做|-5|=5.
0的绝对值是0,
记做|0|=0.
5
5
0
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值。
一个数a的绝对值表示为 .
|a|
形成概念:
读作:“
解:在数轴上表示各数如图所示:
∵表示-1.6的点到原点的距离是1.6, ∴
∵表示 的点到原点的距离是 , ∴
∵表示0的点到原点的距离是0, ∴
∵表示-10的点到原点的距离是10,∴
∵表示10的点到原点的距离是10,∴
例1 求下列各数的绝对值:
0的绝对值是0.
协同探究
正数的绝对值是它本身,
负数的绝对值是它的相反数
任何一个有理数的绝对值都是非负数!|a|≥0
互为相反数的两个数的绝对值相等。
知识过关
①一个数在数轴上对应的点到原点的 距离 叫作这个数的绝对值.
②一个正数的绝对值是 它本身 ;一个负数的绝对值是 它的相反数 ;0的绝对值是 0 .
③互为相反数的两个数的绝对值 相等 .
检测评价
距离
它本身
它的相反数
0
相等
考点一: 绝对值的概念
1. -2025的绝对值是( A )
2.已知有理数a,b,c满足|a|>|b|>|c|,这三个数在数轴上对应的点的位置可能是( A )
考点二: 绝对值的性质
[2023·台州](1)已知|a|=|-2|,则a等于( D )
(2)下列说法不正确的是( C )
A. 任意一个有理数的绝对值不一定是正数
B. 负数的绝对值是它的相反数
C. 如果两个数的绝对值相等,那么这两个数相等
D. 0的绝对值是0
考点二: 绝对值的性质
[2024·衢州模拟]用符号语言表述“负数的绝对值等于它的相反数”正确的是( D )
A. |-a|=a
B. |a|=-a
C. |-a|=a(a<0)
D. |a|=-a(a<0)
|x-4|+|y+6|=0,求x+y的值
考点三: 与绝对值有关的计算
已知a=-2,b=1,则|a|+|-b|的值为( A )
A. 3 B. 1 C. 0 D. -1
[教材母题]计算:|-7|+ - ;
考点四: 情境题·生活应用
某出租车司机一日从公司出发,在东西方向的人民路上连续接送5批客人,行驶路程记录如下(规定向东为正,向西为负,单位:km):
第1批 第2批 第3批 第4批 第5批
5 2 -4 -3 10
若该出租车每千米耗油0.08升,那么在这个过程中共耗油多少升?
考点五: 新考法·阅读类比法
同学们都知道,|7-(-1)|表示7与-1之差的绝对值,实际上也可以理解为7与-1两数在数轴上所对应的两点之间的距离.如|x-6|的几何意义是数轴上表示数x的点与表示数6的点之间的距离.试探索:
(1)求|3-(-2)|= ;若|x-(-2)|=3,
则x= ;
(2)|x-1|+|x-(-3)|的最小值是 ;
(3)求当x为何值时,|x-(-1)|+|x-2|+|x-4|的值最小,最小值多少?
课堂总结
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
