浙教版八上1.5三角形全等的判定(第3课时) 同步教学课件(共26张PPT)
文档属性
| 名称 | 浙教版八上1.5三角形全等的判定(第3课时) 同步教学课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 05:26:45 | ||
图片预览



文档简介
(共26张PPT)
第1章 三角形的初步认识
1.5三角形全等的判定(第3课时)
(浙教版)八年级
上
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
板书设计
01
教学目标
01
02
探索并正确理解三角形全等的判定方法“角边角”和“角角边”.
会用三角形全等的判定方法“角边角”和“角角边”证明两个三角形全等.
02
新知导入
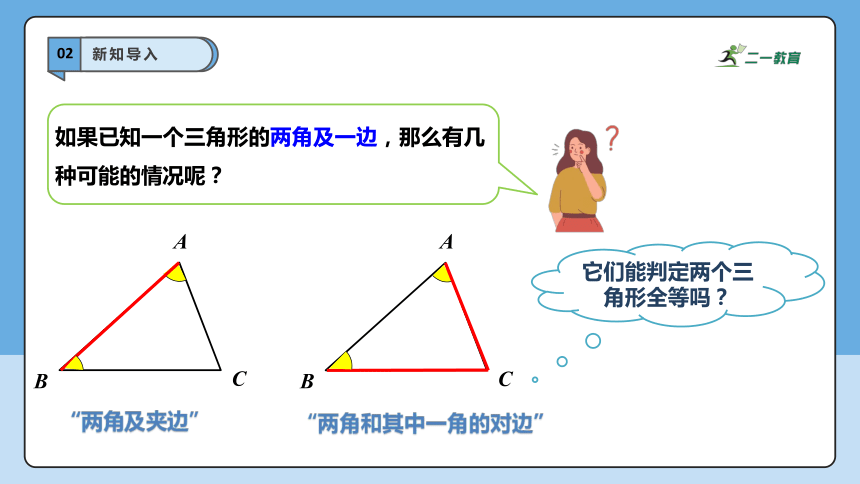
如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
“两角及夹边”
“两角和其中一角的对边”
它们能判定两个三角形全等吗?
A
B
C
03
新知讲解
合作学习
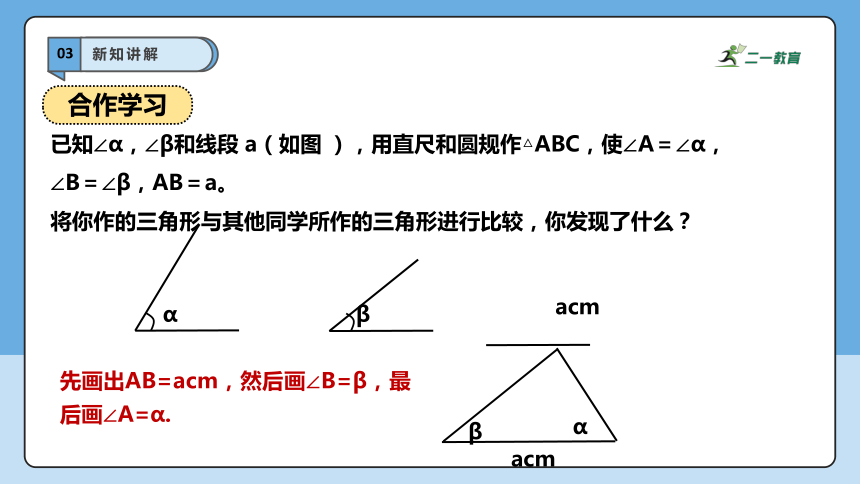
已知∠α,∠β和线段 a(如图 ),用直尺和圆规作△ABC,使∠A=∠α,∠B=∠β,AB=a。
将你作的三角形与其他同学所作的三角形进行比较,你发现了什么?
acm
β
α
先画出AB=acm,然后画∠B=β,最后画∠A=α.
acm
β
α
03
新知探究
三角形全等的判定定理(ASA):
两个角及其夹边分别相等的两个三角形全等
(简写成“角边角”或“ASA”)
在△ABC 与 △ A′B′C′ 中,
∴△ABC ≌△A′B′C′
∠B =∠B′
BC = B′C′
∠C =∠C′
几何语言:
A
B
C
A'
B'
C'
(ASA)
03
新知讲解
做一做
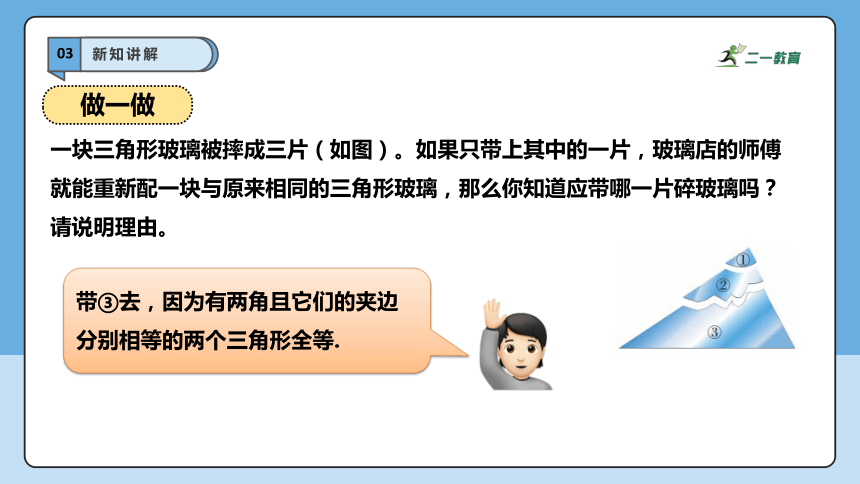
一块三角形玻璃被摔成三片(如图)。如果只带上其中的一片,玻璃店的师傅就能重新配一块与原来相同的三角形玻璃,那么你知道应带哪一片碎玻璃吗?请说明理由。
带③去,因为有两角且它们的夹边分别相等的两个三角形全等.
03
新知讲解
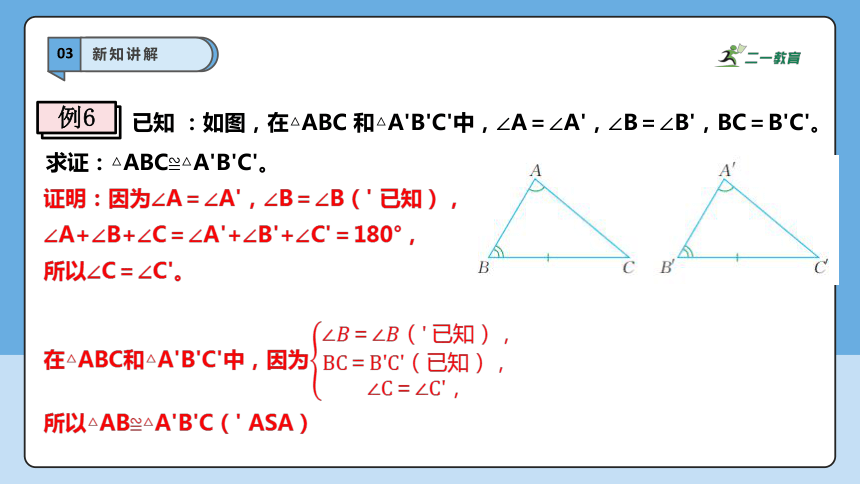
已知 :如图,在△ABC 和△A'B'C'中,∠A=∠A',∠B=∠B',BC=B'C'。求证:△ABC≌△A'B'C'。
例6
证明:因为∠A=∠A',∠B=∠B(' 已知),
∠A+∠B+∠C=∠A'+∠B'+∠C'=180°,
所以∠C=∠C'。
在△ABC和△A'B'C'中,因为
所以△AB≌△A'B'C(' ASA)
03
新知讲解
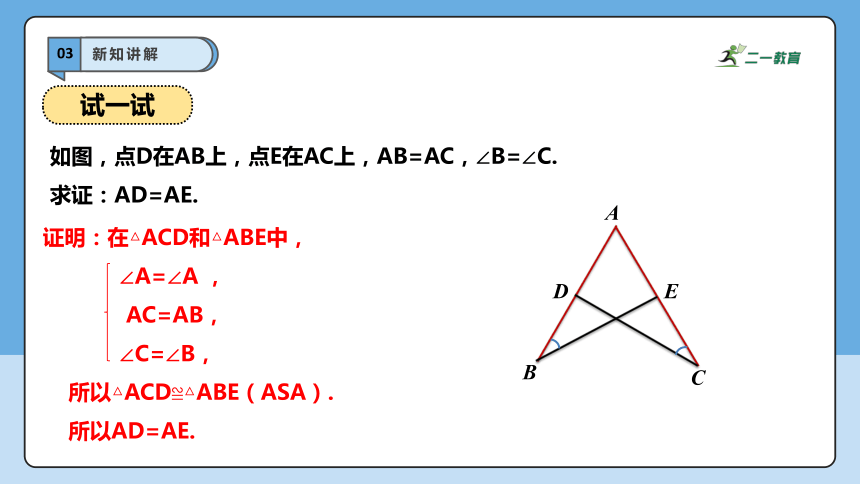
试一试
如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.
求证:AD=AE.
证明:在△ACD和△ABE中,
∠A=∠A ,
AC=AB,
∠C=∠B,
所以△ACD≌△ABE(ASA).
所以AD=AE.
D
E
B
C
A
03
新知讲解
思考
如果两个三角形的两角和其中一组等角的对边分别相等,那么这两个三角形全等吗?
C'
A'
B'
C
A
B
提示:三角形的内角和定理
已知:∠A =∠A′,∠B =∠B′,BC = B′C′.
求证:△ABC ≌△A′B′C′
03
新知探究
在△ABC 中, ∠A +∠B +∠C = 180°
∠B =∠B'
BC = B′C′
∠C = ∠C'
所以△ABC ≌△A′B′C′
证明:
C
A
B
C'
A'
B'
(ASA)
所以∠C = 180° –∠A –∠B
同理∠C' = 180° –∠A' –∠B'
又 ∠A =∠A', ∠B =∠B',
所以∠C = ∠C'
在△ABC 和△A′B′C′ 中,
03
新知探究
三角形全等的判定定理(AAS ):
两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS ”)
在△ABC 与 △ A′B′C′ 中,
∴△ABC ≌△A′B′C′
∠A =∠A′
∠B =∠B′
BC = B′C′
几何语言:
A
B
C
A'
B'
C'
(AAS)
03
新知讲解
已知:如图,AC 与 DB 相交于点 P,∠1=∠2,∠ABC=∠DCB。
求证:AP=DP,BP=CP。
例7
分析:要证 AP=DP,BP=CP,可通过证明△ABP≌△DCP 得到。而在△ABP 和△DCP 中,只有∠APB=∠DPC,还缺两个条件,需要通过证明△ABC △DCB得到。
03
新知讲解
已知:如图,AC 与 DB 相交于点 P,∠1=∠2,∠ABC=∠DCB。
求证:AP=DP,BP=CP。
例7
证明:在△ABC和△DCB中,
因为
所以△ABC △DCB(ASA),
所以AB=DC,∠A=∠D。
在△ABP和△DCP中,
因为
所以△ABP≌△DCP(AAS),
所以AP=DP,BP=CP。
03
新知讲解
试一试
如图,在△ABC和△ADC中,∠B=∠D=90°,∠BAC=∠DAC.
求证:△ABC≌△ADC.
证明:在△ABC和△ADC中,
∠B=∠D,
∠BAC=∠DAC,
AC=AC,
∴△ABC≌△ADC(AAS).
┐
A
B
D
C
┐
04
课堂练习
基础题
1.如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中一定和△ABC全等的图形是( )
A.甲、乙 B.甲、丙
C.乙、丙 D.乙
C
04
课堂练习
基础题
2.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B.AD=AE
C.BD=CE D.BE=CD
D
3. 如图,∠1=∠2,∠C=∠B,则能直接判定△ACD≌△ABD的依据是( A )
A. AAS B. ASA C. SSS D. SAS
A
A. AAS B. ASA C. SSS D. SAS
04
课堂练习
基础题
4. 如图,点A,B,D,E在同一条直线上,AB=DE,AC∥DF,BC∥EF.
求证:△ABC≌△DEF.
证明:因为AC∥DF,所以∠A=∠EDF.
又因为BC∥EF,所以∠ABC=∠E.
在△ABC和△DEF中,因为
所以△ABC≌△DEF(ASA)
04
课堂练习
提升题
1. 如图,在△ABE和△ACD中,点D,E分别在线段AB,AC上,CD与BE相交于点O,AB=AC,现添加下列条件仍不能判定△ABE≌△ACD的是( B )
A. ∠B=∠C B. BE=CD
B
C. BD=CE D. AD=AE
04
课堂练习
提升题
2. 如图,AB∥CD,AB=CD,点B,E,F,D在同一条直线上,∠A=∠C. 有下列结论:① △ABE≌△CDF;② AE=CF;③ BE=DF;④ BF=DE;⑤ AE∥CF. 其中,正确的是 ①②③④⑤ (填序号).
①②③④⑤
04
课堂练习
拓展题
1. 已知CD是经过∠BCA的顶点C的一条直线,CA=CB,E,F是直线CD上两点,且∠BEC=∠CFA=α.若直线CD经过∠BCA的内部,且点E,F在射线CD上,请解决下面两个问题:
(1) 如图①,若∠BCA=90°,α=90°,则BE = CF,EF = |BE-AF|(填“>”“<”或“=”),请说明理由;
=
=
解:(1) 理由:因为∠BCA=90°,α=90°,所以∠BCE+∠ACF=90°,∠BCE+∠CBE=90°.所以∠CBE=∠ACF.
在△BCE和△CAF中,因为 所以△BCE≌△CAF(AAS).所以BE=CF,CE=AF. 所以EF=|CF-CE|=
|BE-AF|.
04
课堂练习
拓展题
(2) 如图②,若0°<∠BCA<180°,添加一个关于α与∠BCA关系的条件: ∠BCA=180°-α ,可以使(1)中的两个结论仍然成立,并加以证明.
∠BCA=180°-α
(2) 因为∠CBE+∠BCE=180°-∠BEC=180°-α,∠BCA=180°-α,所以∠CBE+∠BCE=∠BCA.
因为∠ACF+∠BCE=∠BCA,所以∠CBE=∠ACF.
在△BCE和△CAF中,因为
所以△BCE≌△CAF(AAS).
所以BE=CF,CE=AF. 所以EF=|CF-CE|=|BE-AF|
05
课堂小结
1.三角形全等的判定定理(ASA):
两个角及其夹边分别相等的两个三角形全等
(简写成“角边角”或“ASA”)
2.三角形全等的判定定理(AAS):
两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS ”)
06
板书设计
1.5三角形全等的判定(第3课时)
1.三角形全等的判定定理(ASA):
两个角及其夹边分别相等的两个三角形全等
(简写成“角边角”或“ASA”)
2.三角形全等的判定定理(AAS):
两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS ”)
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第1章 三角形的初步认识
1.5三角形全等的判定(第3课时)
(浙教版)八年级
上
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
板书设计
01
教学目标
01
02
探索并正确理解三角形全等的判定方法“角边角”和“角角边”.
会用三角形全等的判定方法“角边角”和“角角边”证明两个三角形全等.
02
新知导入
如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
“两角及夹边”
“两角和其中一角的对边”
它们能判定两个三角形全等吗?
A
B
C
03
新知讲解
合作学习
已知∠α,∠β和线段 a(如图 ),用直尺和圆规作△ABC,使∠A=∠α,∠B=∠β,AB=a。
将你作的三角形与其他同学所作的三角形进行比较,你发现了什么?
acm
β
α
先画出AB=acm,然后画∠B=β,最后画∠A=α.
acm
β
α
03
新知探究
三角形全等的判定定理(ASA):
两个角及其夹边分别相等的两个三角形全等
(简写成“角边角”或“ASA”)
在△ABC 与 △ A′B′C′ 中,
∴△ABC ≌△A′B′C′
∠B =∠B′
BC = B′C′
∠C =∠C′
几何语言:
A
B
C
A'
B'
C'
(ASA)
03
新知讲解
做一做
一块三角形玻璃被摔成三片(如图)。如果只带上其中的一片,玻璃店的师傅就能重新配一块与原来相同的三角形玻璃,那么你知道应带哪一片碎玻璃吗?请说明理由。
带③去,因为有两角且它们的夹边分别相等的两个三角形全等.
03
新知讲解
已知 :如图,在△ABC 和△A'B'C'中,∠A=∠A',∠B=∠B',BC=B'C'。求证:△ABC≌△A'B'C'。
例6
证明:因为∠A=∠A',∠B=∠B(' 已知),
∠A+∠B+∠C=∠A'+∠B'+∠C'=180°,
所以∠C=∠C'。
在△ABC和△A'B'C'中,因为
所以△AB≌△A'B'C(' ASA)
03
新知讲解
试一试
如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.
求证:AD=AE.
证明:在△ACD和△ABE中,
∠A=∠A ,
AC=AB,
∠C=∠B,
所以△ACD≌△ABE(ASA).
所以AD=AE.
D
E
B
C
A
03
新知讲解
思考
如果两个三角形的两角和其中一组等角的对边分别相等,那么这两个三角形全等吗?
C'
A'
B'
C
A
B
提示:三角形的内角和定理
已知:∠A =∠A′,∠B =∠B′,BC = B′C′.
求证:△ABC ≌△A′B′C′
03
新知探究
在△ABC 中, ∠A +∠B +∠C = 180°
∠B =∠B'
BC = B′C′
∠C = ∠C'
所以△ABC ≌△A′B′C′
证明:
C
A
B
C'
A'
B'
(ASA)
所以∠C = 180° –∠A –∠B
同理∠C' = 180° –∠A' –∠B'
又 ∠A =∠A', ∠B =∠B',
所以∠C = ∠C'
在△ABC 和△A′B′C′ 中,
03
新知探究
三角形全等的判定定理(AAS ):
两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS ”)
在△ABC 与 △ A′B′C′ 中,
∴△ABC ≌△A′B′C′
∠A =∠A′
∠B =∠B′
BC = B′C′
几何语言:
A
B
C
A'
B'
C'
(AAS)
03
新知讲解
已知:如图,AC 与 DB 相交于点 P,∠1=∠2,∠ABC=∠DCB。
求证:AP=DP,BP=CP。
例7
分析:要证 AP=DP,BP=CP,可通过证明△ABP≌△DCP 得到。而在△ABP 和△DCP 中,只有∠APB=∠DPC,还缺两个条件,需要通过证明△ABC △DCB得到。
03
新知讲解
已知:如图,AC 与 DB 相交于点 P,∠1=∠2,∠ABC=∠DCB。
求证:AP=DP,BP=CP。
例7
证明:在△ABC和△DCB中,
因为
所以△ABC △DCB(ASA),
所以AB=DC,∠A=∠D。
在△ABP和△DCP中,
因为
所以△ABP≌△DCP(AAS),
所以AP=DP,BP=CP。
03
新知讲解
试一试
如图,在△ABC和△ADC中,∠B=∠D=90°,∠BAC=∠DAC.
求证:△ABC≌△ADC.
证明:在△ABC和△ADC中,
∠B=∠D,
∠BAC=∠DAC,
AC=AC,
∴△ABC≌△ADC(AAS).
┐
A
B
D
C
┐
04
课堂练习
基础题
1.如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中一定和△ABC全等的图形是( )
A.甲、乙 B.甲、丙
C.乙、丙 D.乙
C
04
课堂练习
基础题
2.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B.AD=AE
C.BD=CE D.BE=CD
D
3. 如图,∠1=∠2,∠C=∠B,则能直接判定△ACD≌△ABD的依据是( A )
A. AAS B. ASA C. SSS D. SAS
A
A. AAS B. ASA C. SSS D. SAS
04
课堂练习
基础题
4. 如图,点A,B,D,E在同一条直线上,AB=DE,AC∥DF,BC∥EF.
求证:△ABC≌△DEF.
证明:因为AC∥DF,所以∠A=∠EDF.
又因为BC∥EF,所以∠ABC=∠E.
在△ABC和△DEF中,因为
所以△ABC≌△DEF(ASA)
04
课堂练习
提升题
1. 如图,在△ABE和△ACD中,点D,E分别在线段AB,AC上,CD与BE相交于点O,AB=AC,现添加下列条件仍不能判定△ABE≌△ACD的是( B )
A. ∠B=∠C B. BE=CD
B
C. BD=CE D. AD=AE
04
课堂练习
提升题
2. 如图,AB∥CD,AB=CD,点B,E,F,D在同一条直线上,∠A=∠C. 有下列结论:① △ABE≌△CDF;② AE=CF;③ BE=DF;④ BF=DE;⑤ AE∥CF. 其中,正确的是 ①②③④⑤ (填序号).
①②③④⑤
04
课堂练习
拓展题
1. 已知CD是经过∠BCA的顶点C的一条直线,CA=CB,E,F是直线CD上两点,且∠BEC=∠CFA=α.若直线CD经过∠BCA的内部,且点E,F在射线CD上,请解决下面两个问题:
(1) 如图①,若∠BCA=90°,α=90°,则BE = CF,EF = |BE-AF|(填“>”“<”或“=”),请说明理由;
=
=
解:(1) 理由:因为∠BCA=90°,α=90°,所以∠BCE+∠ACF=90°,∠BCE+∠CBE=90°.所以∠CBE=∠ACF.
在△BCE和△CAF中,因为 所以△BCE≌△CAF(AAS).所以BE=CF,CE=AF. 所以EF=|CF-CE|=
|BE-AF|.
04
课堂练习
拓展题
(2) 如图②,若0°<∠BCA<180°,添加一个关于α与∠BCA关系的条件: ∠BCA=180°-α ,可以使(1)中的两个结论仍然成立,并加以证明.
∠BCA=180°-α
(2) 因为∠CBE+∠BCE=180°-∠BEC=180°-α,∠BCA=180°-α,所以∠CBE+∠BCE=∠BCA.
因为∠ACF+∠BCE=∠BCA,所以∠CBE=∠ACF.
在△BCE和△CAF中,因为
所以△BCE≌△CAF(AAS).
所以BE=CF,CE=AF. 所以EF=|CF-CE|=|BE-AF|
05
课堂小结
1.三角形全等的判定定理(ASA):
两个角及其夹边分别相等的两个三角形全等
(简写成“角边角”或“ASA”)
2.三角形全等的判定定理(AAS):
两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS ”)
06
板书设计
1.5三角形全等的判定(第3课时)
1.三角形全等的判定定理(ASA):
两个角及其夹边分别相等的两个三角形全等
(简写成“角边角”或“ASA”)
2.三角形全等的判定定理(AAS):
两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS ”)
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
