浙教版九年级下数学《1.1 锐角三角函数》教案
文档属性
| 名称 | 浙教版九年级下数学《1.1 锐角三角函数》教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 167.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-03 00:00:00 | ||
图片预览

文档简介
课题:1.1锐角三角函数(2)
教学目标
(一)教学知识点
1.经历探索30°、45°、60°角的三角函数值的过程,能够进行有关的推理.进一步体会三角函数的意义.
2.能够进行30°、45°、60°角的三角函数值的计算.
3.能够根据30°、45°、60°的三角函数值说明相应的锐角的大小.
(二)思维训练要求
1.经历探索30°、45°、60°角的三角函数值的过程,发展学生观察、分析、发现的能力.
2.培养学生把实际问题转化为数学问题的能力.
(三)情感与价值观要求
1.积极参与数学活动,对数学产生好奇心.培养学生独立思考问题的习惯.
2.在数学活动中获得成功的体验,锻炼克服困难的意志,建立自信心.
教学重点
1.探索30°、45°、60°角的三角函数值.
2.能够进行含30°、45°、60°角的三角函数值的计算.
3.比较锐角三角函数值的大小.
教学难点
进一步体会三角函数的意义.
教学过程
一.讲授新课
探索30°、45°、60°角的三角函数值.
[师]观察一副三角尺,其中有几个锐角?它们分别等于多少度?
[生]一副三角尺中有四个锐角,它们分别是30°、60°、45°、45°.
[师]sin30°等于多少呢?你是怎样得到的?与同伴交流.
[生]sin30°=.
sin30°表示在直角三角形中,30°角的对边与斜边的比值,与直角三角形的大小无关.我们不妨设30°角所对的边为a(如图所示),根据“直角三角形中30°角所对的边等于斜边的一半”的性质,则斜边等于2a.根据勾股定理,可知30°角的邻边为a,所以sin30°=.
[师]cos30°等于多少?tan30°呢?
[生]cos30°= tan30°=
[师]我们求出了30°角的三个三角函数值,还有两个特殊角——60°、45°,它们的三角函数值分别是多少?你是如何得到的?
[生]求60°的三角函数值可以利用求30°角三角函数值的三角形.因为30°角的对边和邻边分别是60°角的邻边和对边.利用上图,很容易求得sin60°=,
cos60°=, tan60°=.
[生]也可以利用上节课我们得出的结论:一锐角的正弦等于它余角的余弦,一锐角的余弦等于它余角的正弦.可知sin60°=cos(90°-60°)=cos30°=cos60°=sin(90°-
60°)=sin30°=.
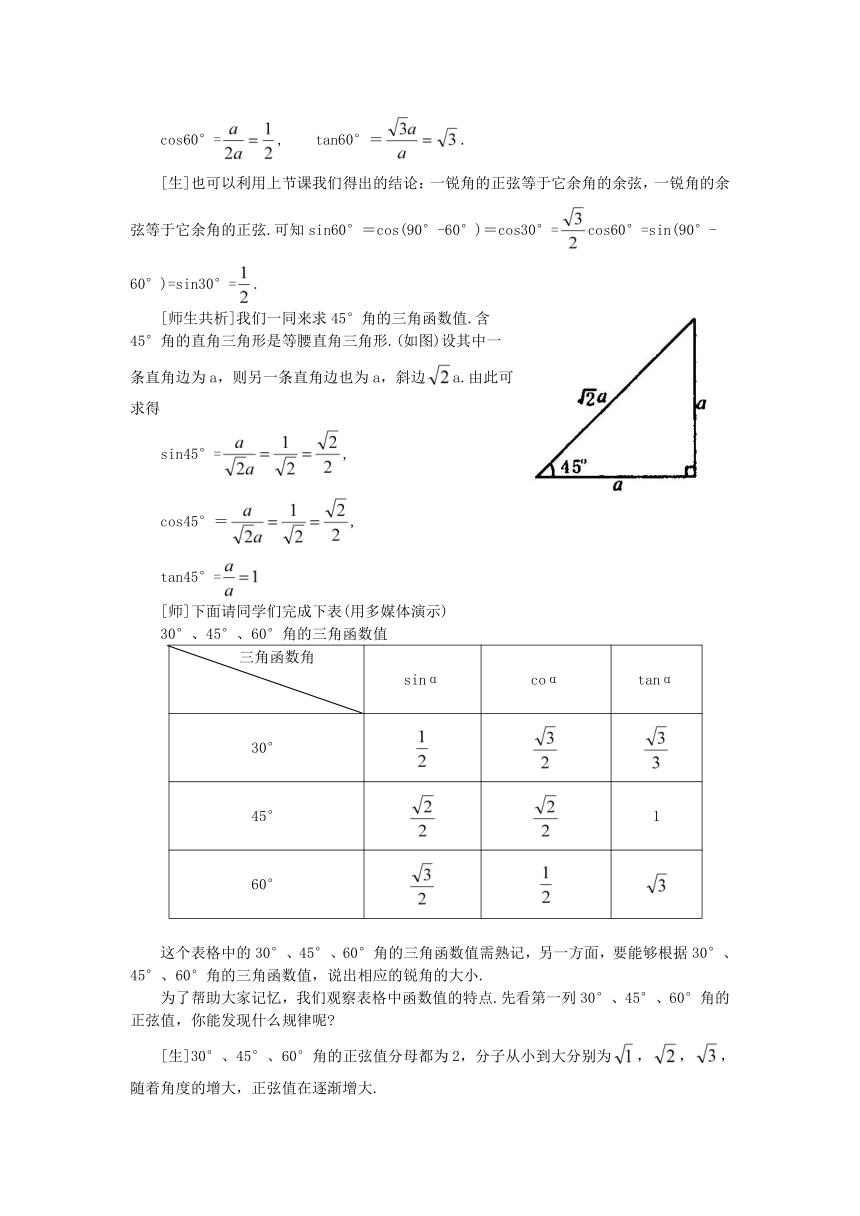
[师生共析]我们一同来求45°角的三角函数值.含
45°角的直角三角形是等腰直角三角形.(如图)设其中一
条直角边为a,则另一条直角边也为a,斜边a.由此可
求得
sin45°=,
cos45°=,
tan45°=
[师]下面请同学们完成下表(用多媒体演示)
30°、45°、60°角的三角函数值
三角函数角
sinα
coα
tanα
30°
45°
1
60°
这个表格中的30°、45°、60°角的三角函数值需熟记,另一方面,要能够根据30°、45°、60°角的三角函数值,说出相应的锐角的大小.
为了帮助大家记忆,我们观察表格中函数值的特点.先看第一列30°、45°、60°角的正弦值,你能发现什么规律呢?
[生]30°、45°、60°角的正弦值分母都为2,分子从小到大分别为,,,随着角度的增大,正弦值在逐渐增大.
[师]再来看第二列函数值,有何特点呢?
[生]第二列是30°,45°、60°角的余弦值,它们的分母也都是2,而分子从大到小分别为,,,余弦值随角度的增大而减小.
[师]第三列呢?
[生]第三列是30°、45°、60°角的正切值,首先45°角是等腰直角三角形中的一个锐角,所以tan45°=1比较特殊.
[师]很好,掌握了上述规律,记忆就方便多了.下面同桌之间可互相检查一下对30°、
45°、60°角的三角函数值的记忆情况.相信同学们一定做得很棒.
二、例题讲解(多媒体演示,师生共同完成)
[例1]计算:
(1)2sin30°-3cos60°;
(2)cos30°-sin45°+tan45°cos60°.
计算:
分析:本题旨在帮助学生巩固特殊角的三角函数值,今后若无特别说明,用特殊角三角函数值进行计算时,一般不取近似值,另外sin260°表示(sin60°)2,cos260°表示
(cos60°)2.
思考:拓展,揭示同一个锐角的三个三角函数的内在关系。
计算:
计算:
例2:如图(见课本),一位同学的手臂长66cm, 当他高举双臂时,指尖高出头顶35cm.问当他的手臂与水平方向成60°角时,指尖高出头顶多少cm(精确到0.1cm)?
分析:审题时注意头部到腋下的不变性,手臂长的已知。
三、随堂练习
应用: 小亮在一倾斜角为30°的斜坡上滑行100米,分别求他沿水平方向和铅垂方向所经过的距离。
分析:100米指的是哪段线段?水平和铅垂距离又指什么?如何应用到三角函数?
(改)某商场有一自动扶梯,其倾斜角为30°.高为7 m,扶梯的长度是多少?
解:扶梯的长度为=14(m),
所以扶梯的长度为14 m.
四、课时小结
本节课总结如下:
(1)探索30°、45°、60°角的三角函数值.
sin30°=,sin45°=,sin60°=;
cos30°=,cos45°= ,cos60°=;
tan30°= ,tan45°=1,tan60°=.
(2)能进行含30°、45°、60°角的三角函数值的计算.
(3)能根据30°、45°、60°角的三角函数值,说出相应锐角的大小.
五、课后作业
如图为住宅区内的两幢楼,它们的高AB=CD=30 m,两楼问的距离AC=24 m,现需了解甲楼对乙楼的采光影响情况.当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高?
(精确到0.1 m,≈1.41,≈1.73)
[过程]根据题意,将实际问题转化为数学问题,当光线从楼顶E,直射到乙楼D点,D点向下便接受不到光线,过D作DB⊥AE(甲楼).在Rt△BDE中.BD=AC=24 m,∠EDB=30°.可求出BE,由于甲、乙楼一样高,所以DF=BE.
[结果]在Kt△BDE中,BE=DB·tan30°=24×=8m.
∵DF=BE,
∴DF=8≈8×1.73=13.84(m).
甲楼的影子在乙楼上的高CD=30-13.84≈16.2(m).
六、板书:
课后反思:
特殊锐角三角函数的得出具有可类比性,学生接受起来较为顺利;
三角函数是种不同于已学过的一次函数、反比例函数、二次函数,它的概念、形式和应用方式都不同,因此在最初学习如何应用时较为“别扭”,学生还处于模仿阶段,既要重视对题目的理解、形成一定的解题思路,也要重视书写格式。
教学目标
(一)教学知识点
1.经历探索30°、45°、60°角的三角函数值的过程,能够进行有关的推理.进一步体会三角函数的意义.
2.能够进行30°、45°、60°角的三角函数值的计算.
3.能够根据30°、45°、60°的三角函数值说明相应的锐角的大小.
(二)思维训练要求
1.经历探索30°、45°、60°角的三角函数值的过程,发展学生观察、分析、发现的能力.
2.培养学生把实际问题转化为数学问题的能力.
(三)情感与价值观要求
1.积极参与数学活动,对数学产生好奇心.培养学生独立思考问题的习惯.
2.在数学活动中获得成功的体验,锻炼克服困难的意志,建立自信心.
教学重点
1.探索30°、45°、60°角的三角函数值.
2.能够进行含30°、45°、60°角的三角函数值的计算.
3.比较锐角三角函数值的大小.
教学难点
进一步体会三角函数的意义.
教学过程
一.讲授新课
探索30°、45°、60°角的三角函数值.
[师]观察一副三角尺,其中有几个锐角?它们分别等于多少度?
[生]一副三角尺中有四个锐角,它们分别是30°、60°、45°、45°.
[师]sin30°等于多少呢?你是怎样得到的?与同伴交流.
[生]sin30°=.
sin30°表示在直角三角形中,30°角的对边与斜边的比值,与直角三角形的大小无关.我们不妨设30°角所对的边为a(如图所示),根据“直角三角形中30°角所对的边等于斜边的一半”的性质,则斜边等于2a.根据勾股定理,可知30°角的邻边为a,所以sin30°=.
[师]cos30°等于多少?tan30°呢?
[生]cos30°= tan30°=
[师]我们求出了30°角的三个三角函数值,还有两个特殊角——60°、45°,它们的三角函数值分别是多少?你是如何得到的?
[生]求60°的三角函数值可以利用求30°角三角函数值的三角形.因为30°角的对边和邻边分别是60°角的邻边和对边.利用上图,很容易求得sin60°=,
cos60°=, tan60°=.
[生]也可以利用上节课我们得出的结论:一锐角的正弦等于它余角的余弦,一锐角的余弦等于它余角的正弦.可知sin60°=cos(90°-60°)=cos30°=cos60°=sin(90°-
60°)=sin30°=.
[师生共析]我们一同来求45°角的三角函数值.含
45°角的直角三角形是等腰直角三角形.(如图)设其中一
条直角边为a,则另一条直角边也为a,斜边a.由此可
求得
sin45°=,
cos45°=,
tan45°=
[师]下面请同学们完成下表(用多媒体演示)
30°、45°、60°角的三角函数值
三角函数角
sinα
coα
tanα
30°
45°
1
60°
这个表格中的30°、45°、60°角的三角函数值需熟记,另一方面,要能够根据30°、45°、60°角的三角函数值,说出相应的锐角的大小.
为了帮助大家记忆,我们观察表格中函数值的特点.先看第一列30°、45°、60°角的正弦值,你能发现什么规律呢?
[生]30°、45°、60°角的正弦值分母都为2,分子从小到大分别为,,,随着角度的增大,正弦值在逐渐增大.
[师]再来看第二列函数值,有何特点呢?
[生]第二列是30°,45°、60°角的余弦值,它们的分母也都是2,而分子从大到小分别为,,,余弦值随角度的增大而减小.
[师]第三列呢?
[生]第三列是30°、45°、60°角的正切值,首先45°角是等腰直角三角形中的一个锐角,所以tan45°=1比较特殊.
[师]很好,掌握了上述规律,记忆就方便多了.下面同桌之间可互相检查一下对30°、
45°、60°角的三角函数值的记忆情况.相信同学们一定做得很棒.
二、例题讲解(多媒体演示,师生共同完成)
[例1]计算:
(1)2sin30°-3cos60°;
(2)cos30°-sin45°+tan45°cos60°.
计算:
分析:本题旨在帮助学生巩固特殊角的三角函数值,今后若无特别说明,用特殊角三角函数值进行计算时,一般不取近似值,另外sin260°表示(sin60°)2,cos260°表示
(cos60°)2.
思考:拓展,揭示同一个锐角的三个三角函数的内在关系。
计算:
计算:
例2:如图(见课本),一位同学的手臂长66cm, 当他高举双臂时,指尖高出头顶35cm.问当他的手臂与水平方向成60°角时,指尖高出头顶多少cm(精确到0.1cm)?
分析:审题时注意头部到腋下的不变性,手臂长的已知。
三、随堂练习
应用: 小亮在一倾斜角为30°的斜坡上滑行100米,分别求他沿水平方向和铅垂方向所经过的距离。
分析:100米指的是哪段线段?水平和铅垂距离又指什么?如何应用到三角函数?
(改)某商场有一自动扶梯,其倾斜角为30°.高为7 m,扶梯的长度是多少?
解:扶梯的长度为=14(m),
所以扶梯的长度为14 m.
四、课时小结
本节课总结如下:
(1)探索30°、45°、60°角的三角函数值.
sin30°=,sin45°=,sin60°=;
cos30°=,cos45°= ,cos60°=;
tan30°= ,tan45°=1,tan60°=.
(2)能进行含30°、45°、60°角的三角函数值的计算.
(3)能根据30°、45°、60°角的三角函数值,说出相应锐角的大小.
五、课后作业
如图为住宅区内的两幢楼,它们的高AB=CD=30 m,两楼问的距离AC=24 m,现需了解甲楼对乙楼的采光影响情况.当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高?
(精确到0.1 m,≈1.41,≈1.73)
[过程]根据题意,将实际问题转化为数学问题,当光线从楼顶E,直射到乙楼D点,D点向下便接受不到光线,过D作DB⊥AE(甲楼).在Rt△BDE中.BD=AC=24 m,∠EDB=30°.可求出BE,由于甲、乙楼一样高,所以DF=BE.
[结果]在Kt△BDE中,BE=DB·tan30°=24×=8m.
∵DF=BE,
∴DF=8≈8×1.73=13.84(m).
甲楼的影子在乙楼上的高CD=30-13.84≈16.2(m).
六、板书:
课后反思:
特殊锐角三角函数的得出具有可类比性,学生接受起来较为顺利;
三角函数是种不同于已学过的一次函数、反比例函数、二次函数,它的概念、形式和应用方式都不同,因此在最初学习如何应用时较为“别扭”,学生还处于模仿阶段,既要重视对题目的理解、形成一定的解题思路,也要重视书写格式。
