1.1认识三角形同步训练

1.1 认识三角形同步训练
一．选择题（共8小题）
1．下列长度的三根小木棒能构成三角形的是（　　）
A．2cm，3cm，5cm B．7cm，4cm，2cm C．3cm，4cm，8cm D．3cm，3cm，4cm
2．下面四个图形中，线段BE是△ABC的高的图是（　　）
A． B． C． D．
3．如图，△ABC中，D为DC上的一点，且S△ABD=S△ACD，则AD为△ABC的（　　）
A．高 B．角平分线 C．中线 D．不能确定
4．如图，共有三角形的个数是（　　）
A．3 B．4 C．5 D．6
5．在△ABC中，若∠A=95°，∠B=40°，则∠C的度数为（　　）
A．35° B．40° C．45° D．50°
6．如图，△ABC中，BO，CO分别是∠ABC，∠ACB的平分线，∠A=50°，
则∠BOC等于（　　）
A．110° B．115° C．120° D．130°
（题3图） （题4图） （题6图）
7．已知△ABC中，∠A=20°，∠B=∠C，那么三角形△ABC是（　　）
A．锐角三角形 B．直角三角形 C．钝角三角形 D．正三角形
8．在△ABC中，∠A：∠B：∠C=3：4：5，则∠C等于（　　）
A．45° B．60° C．75° D．90°
　
二．填空题（共6小题）
9．已知三角形的两边长分别是3cm和7cm，第三边长是偶数，则这个三角形的
周长为　 　　．
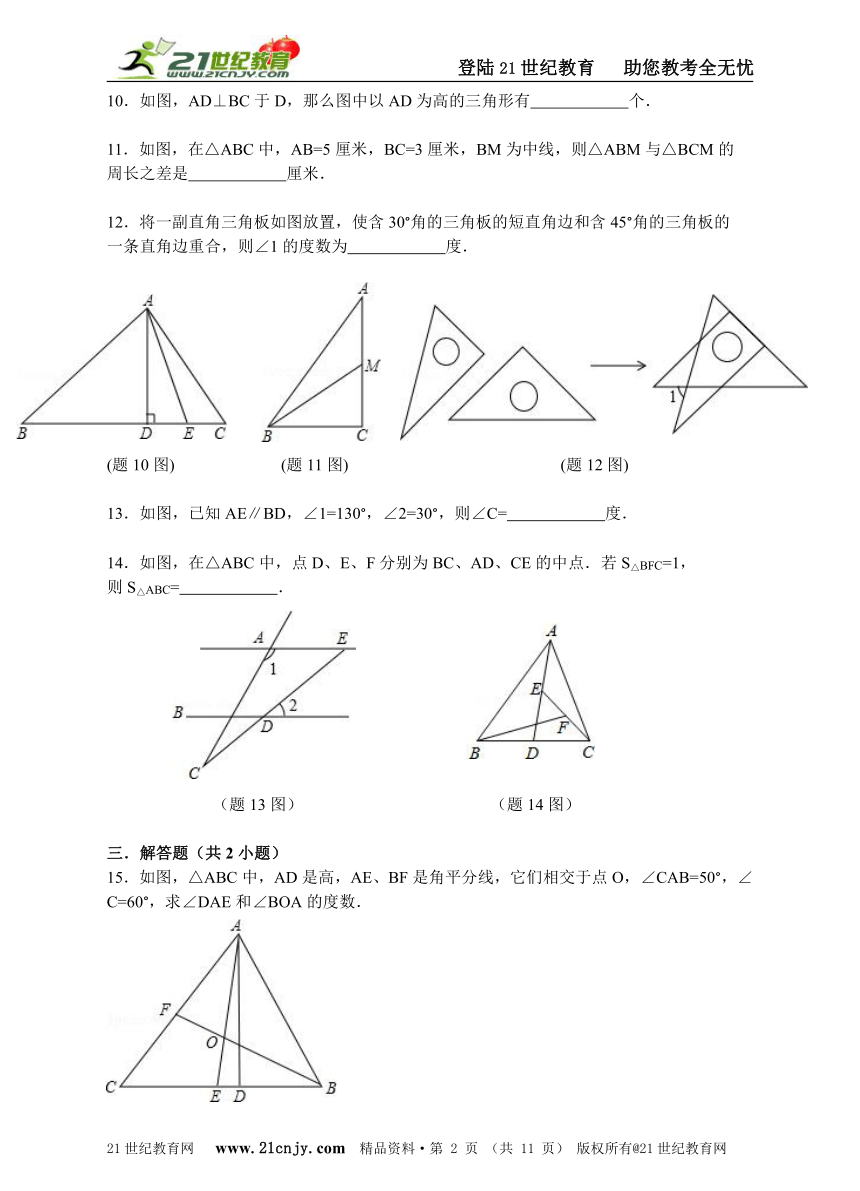
10．如图，AD⊥BC于D，那么图中以AD为高的三角形有　　　　　　个．
11．如图，在△ABC中，AB=5厘米，BC=3厘米，BM为中线，则△ABM与△BCM的
周长之差是　　　　　　厘米．
12．将一副直角三角板如图放置，使含30°角的三角板的短直角边和含45°角的三角板的
一条直角边重合，则∠1的度数为　　　　　　度．
(题10图) (题11图) (题12图)
13．如图，已知AE∥BD，∠1=130°，∠2=30°，则∠C=　　　　　　度．
14．如图，在△ABC中，点D、E、F分别为BC、AD、CE的中点．若S△BFC=1，
则S△ABC=　　　　　　．
　
（题13图） （题14图）
三．解答题（共2小题）
15．如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠CAB=50°，∠C=60°，求∠DAE和∠BOA的度数．21·cn·jy·com
16．图1，线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”．如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试解答下列问题：2-1-c-n-j-y
（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系：　　　　　　；
（2）仔细观察，在图2中“8字形”的个数：　　　　　　个；
（3）图2中，当∠D=50度，∠B=40度时，求∠P的度数．
（4）图2中∠D和∠B为任意角时，其他条件不变，试问∠P与∠D、∠B之间存在着怎样的数量关系．（直接写出结果，不必证明）．　　21*cnjy*com
　

1.1认识三角形同步训练
参考答案与试题解析
　
一．选择题（共8小题）
1．下列长度的三根小木棒能构成三角形的是（　　）
A．2cm，3cm，5cm B．7cm，4cm，2cm C．3cm，4cm，8cm D．3cm，3cm，4cm
【分析】依据三角形任意两边之和大于第三边求解即可．
【解答】解：A、因为2+3=5，所以不能构成三角形，故A错误；
B、因为2+4＜6，所以不能构成三角形，故B错误；
C、因为3+4＜8，所以不能构成三角形，故C错误；
D、因为3+3＞4，所以能构成三角形，故D正确．
故选：D．
【点评】本题主要考查的是三角形的三边关系，掌握三角形的三边关系是解题的关键．
　
2．下面四个图形中，线段BE是△ABC的高的图是（　　）
A． B． C． D．
【分析】根据高的画法知，过点B作AC边上的高，垂足为E，其中线段BE是△ABC的高．
【解答】解：线段BE是△ABC的高的图是D．
故选D．
【点评】三角形的高是指从三角形的一个顶点向对边作垂线，连接顶点与垂足之间的线段．
　
【分析】直接根据三角形的面积公式即可得出结论．
【解答】解：∵S△ABD=S△ACD且△ABD与△ADC同高，
∴BD=CD，即AD为△ABC的中线．
故选C．
【点评】本题考查的是三角形的面积，熟知三角形的面积公式是解答此题的关键．
　
4．如图，共有三角形的个数是（　　）
A．3 B．4 C．5 D．6
【分析】根据三角形的概念：由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形数出三角形的个数．21教育网
【解答】解：图中有：△ABC，△ABD，△ABE，△ACD，△ACE，△ADE，共6个．
故选：D．
【点评】此题主要考查了三角形，关键是掌握三角形的定义，数三角形时，要不重不漏．
　
5．在△ABC中，若∠A=95°，∠B=40°，则∠C的度数为（　　）
A．35° B．40° C．45° D．50°
【分析】在△ABC中，根据三角形内角和是180度来求∠C的度数．
【解答】解：∵三角形的内角和是180°，
又∠A=95°，∠B=40°
∴∠C=180°﹣∠A﹣∠B
=180°﹣95°﹣40°=45°，故选C．
【点评】本题考查了三角形内角和定理，利用三角形内角和定理：三角形内角和是180°是解答此题的关键．
　
【分析】根据三角形的内角和定理和角平分线的定义求出∠OBC+∠OCB的度数，再根据三角形的内角和等于180°即可求出∠BOC的度数．www-2-1-cnjy-com
【解答】解：∵∠A=50°，
∴∠ABC+∠ACB=180°﹣∠A=180°﹣50°=130°，
∵BO，CO分别是∠ABC，∠ACB的平分线，
∴∠OBC=∠ABC，∠OCB=∠ACB，
∴∠OBC+∠OCB=（∠ABC+∠ACB）=×130°=65°，
∴∠BOC=180°﹣（∠OBC+∠OCB）=180°﹣65°=115°．故选B．
【点评】本题主要利用三角形的内角和定理和角平分线的定义，熟练掌握定理和概念是解题的关键．
　
7．已知△ABC中，∠A=20°，∠B=∠C，那么三角形△ABC是（　　）
A．锐角三角形 B．直角三角形 C．钝角三角形 D．正三角形
【分析】根据已知条件和三角形的内角和是180度求得各角的度数，再判断三角形的形状．
【解答】解：∵∠A=20°，
∴∠B=∠C=（180°﹣20°）=80°，
∴三角形△ABC是锐角三角形．
故选A．
【点评】主要考查了三角形的内角和是180度．求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件．21cnjy.com
　
8．在△ABC中，∠A：∠B：∠C=3：4：5，则∠C等于（　　）
A．45° B．60° C．75° D．90°
【分析】首先根据∠A：∠B：∠C=3：4：5，求出∠C的度数占三角形的内角和的几分之几；然后根据分数乘法的意义，用180°乘以∠C的度数占三角形的内角和的分率，求出∠C等于多少度即可．2·1·c·n·j·y
【点评】此题主要考查了三角形的内角和定理，要熟练掌握，解答此题的关键是要明确：三角形的内角和是180°．【来源：21cnj*y.co*m】
　
二．填空题（共6小题）
9．已知三角形的两边长分别是3cm和7cm，第三边长是偶数，则这个三角形的周长为　16cm或18cm　．【出处：21教育名师】
【分析】已知两边，则第三边的长度应是大于两边的差，而小于两边的和，这样就可求出第三边长的范围；
再根据第三边长为偶数，可得出第三边的长，将第三边的长加上另外两边长即可得出周长．
　
10．如图，AD⊥BC于D，那么图中以AD为高的三角形有　6　个．
【分析】由于AD⊥BC于D，图中共有6个三角形，它们都有一边在直线CB上，由此即可确定以AD为高的三角形的个数．【来源：21·世纪·教育·网】
【解答】解：∵AD⊥BC于D，
而图中有一边在直线CB上，且以A为顶点的三角形有6个，
∴以AD为高的三角形有6个．
故答案为：6
【点评】此题主要考查了三角形的高，三角形的高可以在三角形外，也可以在三角形内，所以确定三角形的高比较灵活．【版权所有：21教育】
　
【分析】根据中线的定义可得，△ABM与△BCM的周长之差=AB﹣BC，据此即可求解．
【解答】解：△ABM与△BCM的周长之差=AB﹣BC=5﹣3=2（厘米）．
故答案是：2．
【点评】本题考查了中线的定义，理解△ABM与△BCM的周长之差=AB﹣BC是关键．
　
12．将一副直角三角板如图放置，使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合，则∠1的度数为　75　度．21*cnjy*com
【分析】根据三角形三内角之和等于180°求解．
【解答】解：如图．
∵∠3=60°，∠4=45°，
∴∠1=∠5=180°﹣∠3﹣∠4=75°．
故答案为：75．
【点评】考查三角形内角之和等于180°．
　
13．如图，已知AE∥BD，∠1=130°，∠2=30°，则∠C=　20　度．
【分析】根据平行线的性质和三角形的内角和定理求得．
【解答】解：∵AE∥BD，∠1=130°，∠2=30°，
∴∠CBD=∠1=130°．
∵∠BDC=∠2，
∴∠BDC=30°．
在△BCD中，∠CBD=130°，∠BDC=30°，
∴∠C=180°﹣130°﹣30°=20°．
【点评】本题应用的知识点为：三角形的外角与内角的关系及两直线平行，同位角相等．
　
14．如图，在△ABC中，点D、E、F分别为BC、AD、CE的中点．若S△BFC=1，则S△ABC=　4　．21教育名师原创作品
【分析】根据三角形的中线把三角形分成面积相等的两个三角形用S△ABC表示出△ABD、△ACD、△BDE，△CDE的面积，然后表示出△BCE的面积，再表示出△BEF的面积．
【解答】解：如图，连接BE．
∵点D、E分别为BC、AD的中点，
∴S△ABD=S△ACD=S△ABC，
S△BDE=S△ABD=S△ABC，
S△CDE=S△ACD=S△ABC，
∴S△BCE=S△BDE+S△CDE=S△ABC+S△ABC=S△ABC，
∵F是CE的中点，
【点评】本题考查了三角形的面积，主要利用了三角形的中线把三角形分成面积相等的两个三角形，是此类题目常用的方法，要熟练掌握并灵活运用．21世纪教育网版权所有
　
三．解答题（共2小题）
15．如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠CAB=50°，∠C=60°，求∠DAE和∠BOA的度数．
【分析】先利用三角形内角和定理可求∠ABC，在直角三角形ACD中，易求∠DAC；再根据角平分线定义可求∠CBF、∠EAF，可得∠DAE的度数；然后利用三角形外角性质，可先求∠AFB，再次利用三角形外角性质，容易求出∠BOA．
【解答】解：∵∠A=50°，∠C=60°
∴∠ABC=180°﹣50°﹣60°=70°，
又∵AD是高，
∴∠ADC=90°，
∴∠DAC=180°﹣90°﹣∠C=30°，
∵AE、BF是角平分线，
∴∠CBF=∠ABF=35°，∠EAF=25°，
∴∠DAE=∠DAC﹣∠EAF=5°，
∠AFB=∠C+∠CBF=60°+35°=95°，
∴∠BOA=∠EAF+∠AFB=25°+95°=120°，
∴∠DAC=30°，∠BOA=120°．
故∠DAE=5°，∠BOA=120°．
【点评】本题考查了三角形内角和定理、角平分线定义、三角形外角性质．关键是利用角平分线的性质解出∠EAF、∠CBF，再运用三角形外角性质求出∠AFB．
　
16．图1，线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”．如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试解答下列问题：www.21-cn-jy.com
（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系：　∠A+∠D=∠C+∠B　；
（2）仔细观察，在图2中“8字形”的个数：　6　个；
（3）图2中，当∠D=50度，∠B=40度时，求∠P的度数．
（4）图2中∠D和∠B为任意角时，其他条件不变，试问∠P与∠D、∠B之间存在着怎样的数量关系．（直接写出结果，不必证明）．21·世纪*教育网
【分析】（1）根据三角形内角和定理即可得出∠A+∠D=∠C+∠B；
（2）根据“8字形”的定义，仔细观察图形即可得出“8字形”共有6个；
（3）先根据“8字形”中的角的规律，可得∠DAP+∠D=∠P+∠DCP①，∠PCB+∠B=∠PAB+∠P②，再根据角平分线的定义，得出∠DAP=∠PAB，∠DCP=∠PCB，将①+②，可得2∠P=∠D+∠B，进而求出∠P的度数；
（4）同（3），根据“8字形”中的角的规律及角平分线的定义，即可得出2∠P=∠D+∠B．
【解答】解：（1）∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°，∠AOD=∠BOC，
∴∠A+∠D=∠C+∠B； （2分）
（2）①线段AB、CD相交于点O，形成“8字形”；
②线段AN、CM相交于点O，形成“8字形”；
③线段AB、CP相交于点N，形成“8字形”；
④线段AB、CM相交于点O，形成“8字形”；
⑤线段AP、CD相交于点M，形成“8字形”；
⑥线段AN、CD相交于点O，形成“8字形”；
故“8字形”共有6个； （4分）
（3）∠DAP+∠D=∠P+∠DCP，①
∠PCB+∠B=∠PAB+∠P，②（6分）
∵∠DAB和∠BCD的平分线AP和CP相交于点P，
∴∠DAP=∠PAB，∠DCP=∠PCB，（7分）
①+②得：
∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P，（9分）
即2∠P=∠D+∠B，
又∵∠D=50度，∠B=40度，
∴2∠P=50°+40°，
∴∠P=45°；
【点评】本题主要考查了三角形内角和定理，角平分线的定义及阅读理解与知识的迁移能力．（1）中根据三角形内角和定理得出“8字形”中的角的规律；（2）是考查学生的观察理解能力，需从复杂的图形中辨认出“8字形”；（3）（4）直接运用“8字形”中的角的规律解题．