1.5三角形全等的判定同步训练（三）

登陆21世纪教育 助您教考全无忧
1.5 三角形全等的判定同步训练（三）
　
一．选择题（共5小题）
1．如图，已知∠ABC=∠BAD，添加下列条件还不能判定△ABC≌△BAD的是（　　）
( http: / / www.21cnjy.com )
A．AC=BD B．∠CAB=∠DBA C．∠C=∠D D．BC=AD
2．如图，由∠1=∠2，BC=DC，AC=EC，得△ABC≌△EDC的根据是（　　）
( http: / / www.21cnjy.com )
A．SAS B．ASA C．AAS D．SSS
3．下列关于两个三角形全等的说法：
①三个角对应相等的两个三角形全等；
②三条边对应相等的两个三角形全等；
③有两角和其中一个角的对边对应相等的两个三角形全等；
④有两边和一个角对应相等的两个三角形全等．
正确的说法个数是（　　）
A．1个 B．2个 C．3个 D．4个
4．如图，已知等边△ABC中，BD=CE，AD与BE相交于点P，则∠BPD的度数为（　　）
( http: / / www.21cnjy.com )
A．45° B．55° C．60° D．75°
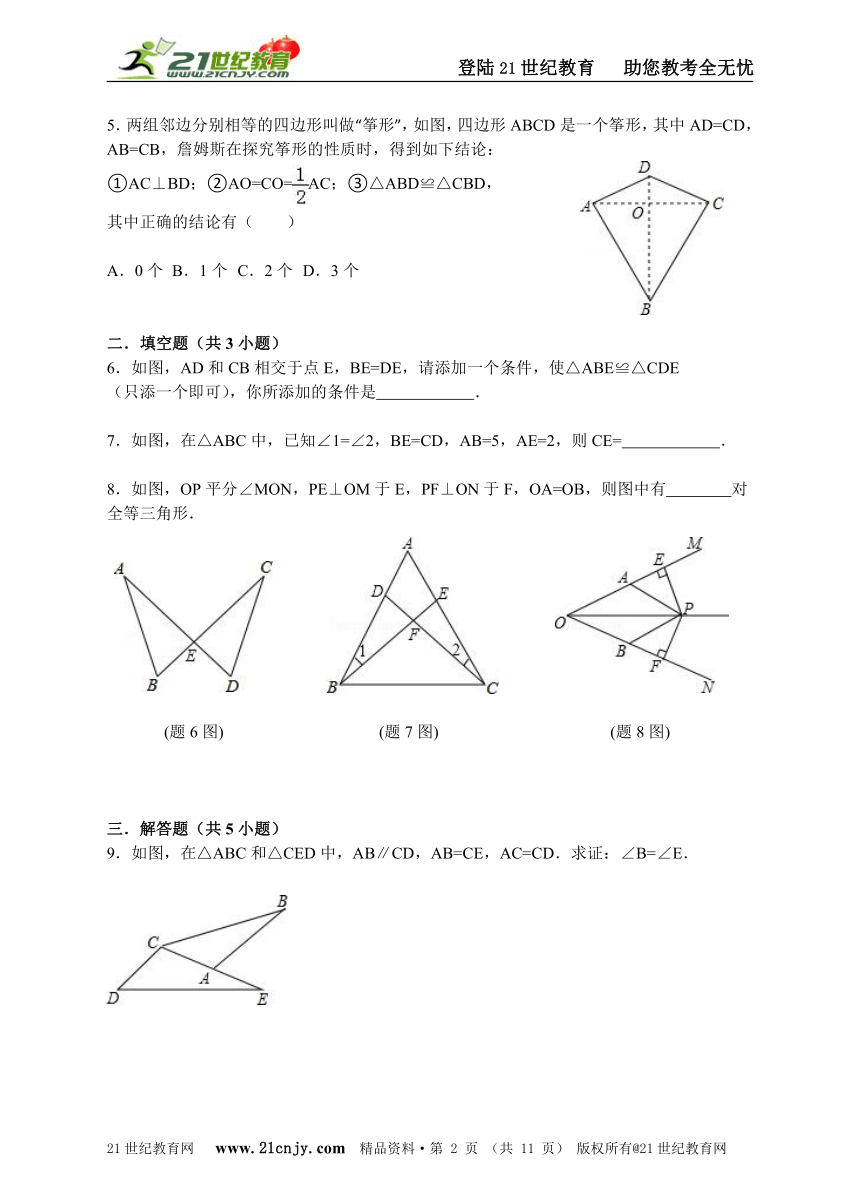
5．两组邻边分别相等的四边形叫做“筝形” ( http: / / www.21cnjy.com )，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，詹姆斯在探究筝形的性质时，得到如下结论：21世纪教育网版权所有
①AC⊥BD；②AO=CO=AC；③△ABD≌△CBD，
其中正确的结论有（　　）
A．0个 B．1个 C．2个 D．3个
　
二．填空题（共3小题）
6．如图，AD和CB相交于点E，BE=DE，请添加一个条件，使△ABE≌△CDE
（只添一个即可），你所添加的条件是　　　　　　．
7．如图，在△ABC中，已知∠1=∠2，BE=CD，AB=5，AE=2，则CE=　　　　　　．
8．如图，OP平分∠MON，PE⊥OM于E，PF⊥ON于F，OA=OB，则图中有　　　　对全等三角形．www.21-cn-jy.com
(题6图) (题7图) (题8图)
　
三．解答题（共5小题）
9．如图，在△ABC和△CED中，AB∥CD，AB=CE，AC=CD．求证：∠B=∠E．
( http: / / www.21cnjy.com )
10．如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，
∠A=∠D．
（1）求证：AB=CD．
（2）若AB=CF，∠B=30°，求∠D的度数．
( http: / / www.21cnjy.com )
11．如图，AB∥CD，E是CD上一点，BE交AD于点F，EF=BF．求证：AF=DF．
( http: / / www.21cnjy.com )
12．如图，∠1=∠2，∠3=∠4，求证：AC=AD．
( http: / / www.21cnjy.com )
13．如图，在△ABC中，已知AB=AC，AD平分∠BAC，点M，N分别在AB，AC边上，AM=2MB，AN=2NC．求证：DM=DN．21cnjy.com
( http: / / www.21cnjy.com )
　
1.5 三角形全等的判定同步训练（三）
参考答案与试题解析
　
一．选择题（共5小题）
( http: / / www.21cnjy.com )
【分析】根据全等三角形的判定：SAS，AAS，ASA，可得答案．
【解答】解：由题意，得∠ABC=∠BAD，AB=BA，
A、∠ABC=∠BAD，AB=BA，AC=BD，（SSA）三角形不全等，故A错误；
B、在△ABC与△BAD中，，△ABC≌△BAD（ASA），故B正确；
C、在△ABC与△BAD中，，△ABC≌△BAD（AAS），故C正确；
D、在△ABC与△BAD中，，△ABC≌△BAD（SAS），故D正确；
故选：A．
【点评】本题考查了全等三角形的判定，判定两 ( http: / / www.21cnjy.com )个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
　
2．如图，由∠1=∠2，BC=DC，AC=EC，得△ABC≌△EDC的根据是（　　）
( http: / / www.21cnjy.com )
A．SAS B．ASA C．AAS D．SSS
【分析】根据∠1=∠2，求出∠BCA=∠DCE，根据SAS证△ABC≌△ECD即可．
【解答】解：∵∠1=∠2，
∴∠1+∠DCA=∠2+∠DCA，
即∠BCA=∠DCE，
在△ABC和△ECD中，
∴△ABC≌△ECD（SAS），故选A
【点评】本题考查了全等三角形的判定的应用，关键是找到证明△ABC和△ECD全等的三个条件，题目比较好，培养了学生运用定理进行推理的能力．21·世纪*教育网
　
3．下列关于两个三角形全等的说法：
①三个角对应相等的两个三角形全等；
②三条边对应相等的两个三角形全等；
③有两角和其中一个角的对边对应相等的两个三角形全等；
④有两边和一个角对应相等的两个三角形全等．
正确的说法个数是（　　）
A．1个 B．2个 C．3个 D．4个
【分析】根据全等三角形的判定方法，此题应采用排除法，对选项逐个进行分析从而确定正确答案．
【解答】解：①不正确，因为判定三角形全等必须有边的参与；
②正确，符合判定方法SSS；
③正确，符合判定方法AAS；
④不正确，此角应该为两边的夹角才能符合SAS．
所以正确的说法有两个．
故选B．
【点评】主要考查全等三角形的判定方法，常用 ( http: / / www.21cnjy.com )的方法有SSS，SAS，AAS，HL等，应该对每一种方法彻底理解真正掌握并能灵活运用．而满足SSA，AAA是不能判定两三角形是全等的．www-2-1-cnjy-com
　
4．如图，已知等边△ABC中，BD=CE，AD与BE相交于点P，则∠BPD的度数为（　　）
( http: / / www.21cnjy.com )
A．45° B．55° C．60° D．75°
【分析】根据等边三角形性质 ( http: / / www.21cnjy.com )得出∠ABD=∠C=60°，AB=BC，证出△ABD≌△BCE，根据全等三角形的性质得出∠BAD=∠CBE，根据三角形外角性质得出∠BPD=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC，即可得出答案．【来源：21cnj*y.co*m】
【解答】解：∵△ABC是等边三角形，
∴∠ABD=∠C=60°，AB=BC，
在△ABD和△BCE中，，
∴△ABD≌△BCE（SAS），
∴∠BAD=∠CBE，
∴∠BPD=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC=60°．
故选C．
【点评】本题考查了等边三角形的性质，全等三角形的性质和判定，三角形外角性质的应用，解此题的关键是求出△ABD≌△BCE．【出处：21教育名师】
　
5．两组邻边分别相等的四边形叫做“筝形 ( http: / / www.21cnjy.com )”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，詹姆斯在探究筝形的性质时，得到如下结论：21教育名师原创作品
①AC⊥BD；②AO=CO=AC；③△ABD≌△CBD，
( http: / / www.21cnjy.com )
【分析】先证明△ABD与△CBD全等，再证明△AOD与△COD全等即可判断．
【解答】解：在△ABD与△CBD中，，
∴△ABD≌△CBD（SSS），
故③正确；
∴∠ADB=∠CDB，
在△AOD与△COD中，，
∴△AOD≌△COD（SAS），
∴∠AOD=∠COD=90°，AO=OC，
∴AC⊥DB，
故①②正确；故选D
【点评】此题考查全等三角形的判定和性质，关键是根据SSS证明△ABD与△CBD全等和利用SAS证明△AOD与△COD全等．【版权所有：21教育】
　
二．填空题（共3小题）
6．如图，AD和CB相交于点E，BE=DE，请添加一个条件，使△ABE≌△CDE（只添一个即可），你所添加的条件是　AE=CE　．21*cnjy*com
( http: / / www.21cnjy.com )
【分析】由题意得，BE=DE，∠AEB=∠CED（对顶角），可选择利用AAS、SAS进行全等的判定，答案不唯一．
【解答】解：添加AE=CE，
在△ABE和△CDE中，
∵，
∴△ABE≌△CDE（SAS），
故答案为：AE=CE．
【点评】本题考查了全等三角形的判定，属于开放型题目，解答本题需要同学们熟练掌握三角形全等的几种判定定理．【来源：21·世纪·教育·网】
　
7．如图，在△ABC中，已知∠1=∠2，BE=CD，AB=5，AE=2，则CE=　3　．
( http: / / www.21cnjy.com )
【分析】由已知条件易证△ABE≌△ACD，再根据全等三角形的性质得出结论．
( http: / / www.21cnjy.com )
【点评】本题主要考查了全等三角形的性质和判定，熟记定理是解题的关键．
　
8．如图，OP平分∠MON，PE⊥OM于E，PF⊥ON于F，OA=OB，则图中有　3　对全等三角形．2·1·c·n·j·y
( http: / / www.21cnjy.com )
【分析】由OP平分∠MON，PE⊥ ( http: / / www.21cnjy.com )OM于E，PF⊥ON于F，得到PE=PF，∠1=∠2，证得△AOP≌△BOP，再根据△AOP≌△BOP，得出AP=BP，于是证得△AOP≌△BOP，和Rt△AOP≌Rt△BOP．　　21*cnjy*com
【解答】解：OP平分∠MON，PE⊥OM于E，PF⊥ON于F，
∴PE=PF，∠1=∠2，
在△AOP与△BOP中，
，
∴△AOP≌△BOP，
∴AP=BP，
在△EOP与△FOP中，
，
∴△EOP≌△FOP，
在Rt△AEP与Rt△BFP中，
，
∴Rt△AEP≌Rt△BFP，
∴图中有3对全等三角形，
故答案为：3．
( http: / / www.21cnjy.com )　
三．解答题（共5小题）
9．如图，在△ABC和△CED中，AB∥CD，AB=CE，AC=CD．求证：∠B=∠E．
( http: / / www.21cnjy.com )
【分析】根据两直线平行，内错角相等 ( http: / / www.21cnjy.com )可得∠BAC=∠ECD，再利用“边角边”证明△ABC和△CED全等，然后根据全等三角形对应角相等证明即可．2-1-c-n-j-y
【解答】证明：∵AB∥CD，∴∠BAC=∠ECD，
在△ABC和△CED中，，
∴△ABC≌△CED（SAS），∴∠B=∠E．
【点评】本题考查了全等三角形的判定与性质，平行线的性质，熟练掌握三角形全等的判定方法并找出两边的夹角是解题的关键．
　
10．如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，
∠A=∠D．
（1）求证：AB=CD．
（2）若AB=CF，∠B=30°，求∠D的度数．
( http: / / www.21cnjy.com )
【分析】（1）易证得△ABE≌△CDF，即可得AB=CD；
（2）易证得△ABE≌△CDF，即可得AB=CD，又由AB=CF，∠B=30°，即可证得△ABE是等腰三角形，解答即可．
【解答】证明：（1）∵AB∥CD，∴∠B=∠C，
在△ABE和△CDF中，，
∴△ABE≌△CDF（AAS），∴AB=CD；
（2）∵△ABE≌△CDF，∴AB=CD，BE=CF，
∵AB=CF，∠B=30°，
∴AB=BE，∴△ABE是等腰三角形，∴∠D=．
【点评】此题考查全等三角形问题，关键是根据AAS证明三角形全等，再利用全等三角形的性质解答．
　
( http: / / www.21cnjy.com )
【分析】欲证明AF=DF只要证明△ABF≌△DEF即可解决问题．
【解答】证明：∵AB∥CD，
∴∠B=∠FED，
在△ABF和△DEF中，
，
∴△ABF≌△DEF，
∴AF=DF．
( http: / / www.21cnjy.com )
【点评】本题考查全等三角形的判定和性质，平行 ( http: / / www.21cnjy.com )线的性质等知识，解题的关键是熟练掌握全等三角形的判断和性质，熟练掌握平行线的性质，属于基础题，中考常考题型．
　
12．如图，∠1=∠2，∠3=∠4，求证：AC=AD．
( http: / / www.21cnjy.com )
【分析】先证出∠ABC=∠ABD，再由ASA证明△ABC≌△ABD，得出对应边相等即可．
【解答】证明：∵∠3=∠4，
∴∠ABC=∠ABD，
在△ABC和△ABD中，，
∴△ABC≌△ABD（ASA），
∴AC=AD．
【点评】本题考查了全等三角形的判定与性质；熟练掌握全等三角形的判定方法，证明三角形全等是解决问题的关键．21教育网
　
13．如图，在△ABC中，已知AB=AC，AD平分∠BAC，点M，N分别在AB，AC边上，AM=2MB，AN=2NC．求证：DM=DN．21·cn·jy·com
( http: / / www.21cnjy.com )
【分析】首先根据等腰三角形的性质得到AD是顶角的平分线，再利用全等三角形进行证明即可．
【解答】证明：∵AM=2MB，AN=2NC，AB=AC，
∴AM=AN，
∵AB=AC，AD平分∠BAC，
∴∠MAD=∠NAD，
在△AMD与△AND中，
( http: / / www.21cnjy.com )　
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网 www.21cnjy.com 精品资料·第 11 页 （共 11 页） 版权所有@21世纪教育网