《全等三角形》学案+练习+解析

1.4全等三角形
授课日期及时段

教学目的
理解全等三角形的概念，能识别全等三角形中的对应角和对应边
掌握全等三角形的性质
教学内容
【知识梳理】
要点1：全等图形
定义：能够重合的两个图形称为全等图形。
要点2：全等三角形
定义：能够重合的两个三角形称为全等三角形。
2、对应元素：两个全等三角形重合时，能互相重合的顶点叫做全等三角形的对应顶点；
互相重合的边叫做全等三角形的对应边；
互相重合的角叫做全等三角形的对应角。
表示方法：“全等”可用符号“≌”来表示。读作“全等于”。
其中“∽”表示形状相似，“=”表示大小相等。合起来就是形状相同，大小相等，
即“全等”。表示两个全等三角形时，通常把对应顶点的字母写在对应的位置上。
性质：全等三角形对应边相等，对应角相等。
重点剖析：（1）两个三角形全等，就是两个三角形能够互相重合，所以这两个三角形不仅对应边相等， 对应角相等，对应角平分线、对应边上的高线和中线也相等，而且它们的周长、面积也相等。
（2）三角形全等具有传递性，即若△ABC≌△A1B1C1 ,△A1B1C1≌△A2B2C2, 则△ABC≌△A2B2C2。
（3）两个三角形只要能够相互重合，那么它们就全等，与它们的位置无关。
要点3：找全等三角形的对应边，对应角的方法：　
1、若给出对应顶点即可找出对应边和对应角。
2、若给出一些对应边或对应角，则按照对应边所对的角是对应角，
反之，对应角所对的边是对应边就可找出其他几组对应边和对应角。
3、按照两对对应边所夹的角是对应角，两对对应角所夹的边是对应边来准确找出对应角和对应边。
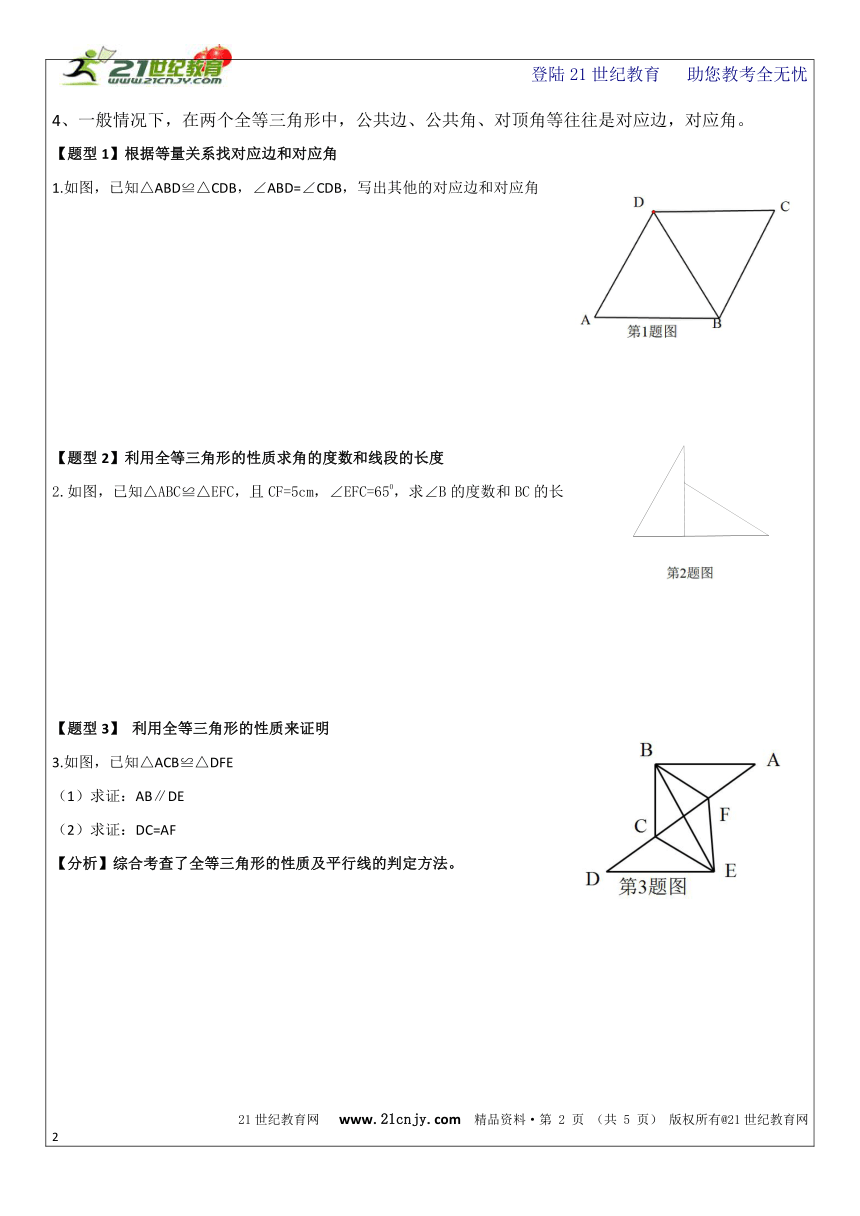
4、一般情况下，在两个全等三角形中，公共边、公共角、对顶角等往往是对应边，对应角。
【题型1】根据等量关系找对应边和对应角
1.如图，已知△ABD≌△CDB，∠ABD=∠CDB，写出其他的对应边和对应角
【题型2】利用全等三角形的性质求角的度数和线段的长度
如图，已知△ABC≌△EFC，且CF=5cm，∠EFC=650，求∠B的度数和BC的长
【题型3】 利用全等三角形的性质来证明
3.如图，已知△ACB≌△DFE
（1）求证：AB∥DE
（2）求证：DC=AF
【分析】综合考查了全等三角形的性质及平行线的判定方法。
【题型4】全等三角形性质的实际应用
4.用同样粗细、同种材料的金属线，制作两个全等的△ABC和△DEF．已知∠B＝∠E，若AC边的质量为20千克，
试求DF边的质量为千克．
【分析】根据全等三角形的性质可得AC＝DF，进而可得答案。
【题型5】利用全等三角形解决面积问题
5.如图，在Rt△ABC中，∠ACB＝90°，且AC＝BC＝4cm，已知△BCD≌△ACE．
求四边形AECD的面积．
【分析】根据全等三角形的性质得出△AEC与△BCD的面积相等，进而解答即可．
【题型6】全等三角形的探究性问题
6.如图，A、D、E三点在同一直线上，且△BAD≌△ACE，试说明：（1）BD＝DE＋CE；（2）△ABD满足什么条件时，BD∥CE？21世纪教育网版权所有
【分析】1）根据全等三角形的性质求出BD＝AE，AD＝CE，代入求出即可；（2）根据全等三角形的性质求出∠E＝∠BDA＝90°，推出∠BDE＝90°，根据平行线的判定求出即可．
题型4：解：∵△ABC≌△DEF，∴AC＝DF，∵AC边的质量为20千克，∴DF边的质量为20千克，故答案为：20．21教育网
题型5：解：∵△BCD≌△ACE，
∴△AEC与△BCD的面积相等，
∴四边形AECD的面积＝△ACD的面积＋△AEC的面积＝△ACD的面积＋△BCD的面积＝△ACB的面积＝12×4×4＝8cm2．21cnjy.com