1.1认识三角形同步练习(1)

1.1认识三角形同步练习1
　
一．选择题（共12小题）
1．（2014?大庆校级模拟）三角形的三边长分别为5，8，x，则最长边x的取值范围是（　　）
A．3＜x＜8 B．5＜x＜13 C．3＜x＜13 D．8＜x＜13
2．（2014秋?杭州期末）如图，在长方形网格中，每个小长方形的长为3，宽为1，A、B两点在网格格点上．若点C也在网格格点上，以A、B、C为顶点的三角形面积为3，则满足条件的点C有（　　）
A．4个 B．7个 C．9个 D．10个
3．（2014秋?岳池县月考）三角形中，最大角α的取值范围是（　　）
A．0°＜α＜90° B．60°＜α＜180° C．60°≤α＜90° D．60°≤α＜180°
4．有5根小木棒，长度分别为2cm、3cm、4cm、5cm、6cm，任意取其中的3根小木棒首尾相接搭三角形，可搭出不同的三角形的个数为（　　）【版权所有：21教育】
A．5个 B．6个 C．7个 D．8个
5．用五根木棒钉成如下四个图形，具有稳定性的有（　　）
A．1个 B．2个 C．3个 D．4个
6．我们知道，以3根火柴为边可以组成一个三角形，那么，用6根火柴为边最多能组成（　　）个三角形．
A．4 B．3 C．2 D．1
7．（2013?海口模拟）如图，在Rt△ADB中，∠D=90°，C为AD上一点，∠ACB=6x，则x值可以是（　　）www-2-1-cnjy-com
A．10° B．20° C．30° D．40°
8．如图，用四个螺丝将四条不可弯曲的木条围成一个木框，不计螺丝大小，其中相邻两螺丝的距离依序为2、3、4、6，且相邻两木条的夹角均可调整．若调整木条的夹角时不破坏此木框，则任两螺丝的距离之最大值为（　　）21*cnjy*com
A．5 B．6 C．7 D．10
9．7条长度均为整数厘米的线段：a1，a2，a3，a4，a5，a6，a7，满足a1＜a2＜a3＜a4＜a5＜a6＜a7，且这7条线段中的任意3条都不能构成三角形．若a1=1厘米，a7=21厘米，则a6能取的值是（　　）　　21*cnjy*com
A．18厘米 B．13厘米 C．8厘米 D．5厘米
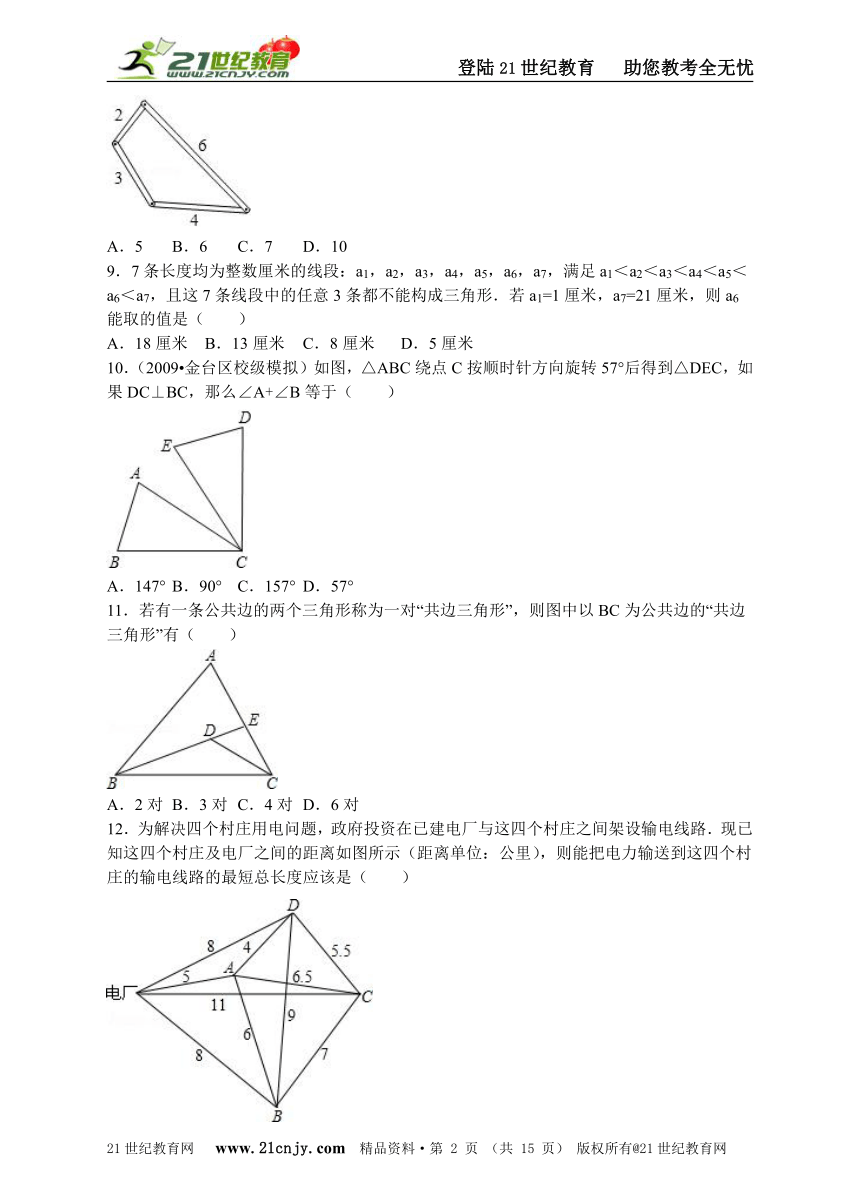
10．（2009?金台区校级模拟）如图，△ABC绕点C按顺时针方向旋转57°后得到△DEC，如果DC⊥BC，那么∠A+∠B等于（　　）
A．147° B．90° C．157° D．57°
11．若有一条公共边的两个三角形称为一对“共边三角形”，则图中以BC为公共边的“共边三角形”有（　　）
A．2对 B．3对 C．4对 D．6对
12．为解决四个村庄用电问题，政府投资在已建电厂与这四个村庄之间架设输电线路．现已知这四个村庄及电厂之间的距离如图所示（距离单位：公里），则能把电力输送到这四个村庄的输电线路的最短总长度应该是（　　）
A．19.5 B．20.5 C．21.5 D．25.5
　
二．填空题（共18小题）
13．（2013?宁波模拟）三条整数长度的线段不能构成三角形的总长度和的最小值为1+2+3=6，四条整数长度的线段任意三条均不能构成三角形的总长度和的最小值为1+2+3+5=11，由此请探究：一根钢管长2009cm，现把此钢管截成整数长的小钢管，使任意三根钢管均不能围成三角形，这根钢管最多可以截成　　　　　　根整数长的小钢管．
14．（2012?烟台）一副三角板叠在一起如图放置，最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上，BC与DE交于点M．如果∠ADF=100°，那么∠BMD为　　　　　　度．
15．（2012?犍为县模拟）某同学在纸上画了四个点，如果把这四个点彼此连接，连成一个图形，则这个图形中会有　　　　　　个三角形出现．【来源：21cnj*y.co*m】
16．（2012?温州二模）如图，已知△ABC的面积是2平方厘米，△BCD的面积是3平方厘米，△CDE的面积是3平方厘米，△DEF的面积是4平方厘米，△EFG的面积是3平方厘米，△FGH的面积是5平方厘米，那么，△EFH的面积是　　　　　　 平方厘米．
17．如图，在△ABC中，点D是BC上一点，∠BAD=80°，AB=AD=DC，则∠C=　　　　　　度．【出处：21教育名师】
　
18．（2016?端州区一模）如图，一扇窗户打开后，用窗钩BC可将其固定，这里所运用的几何原理是　　　　　　．
19．（2016春?淮安月考）一个三角形的两边长分别是3和8，周长是偶数，那么第三边边长是　　　　　　．
20．（2016春?太康县期中）在△ABC中，若∠A=80°，∠B=∠C，则∠C=　　　　　　度．
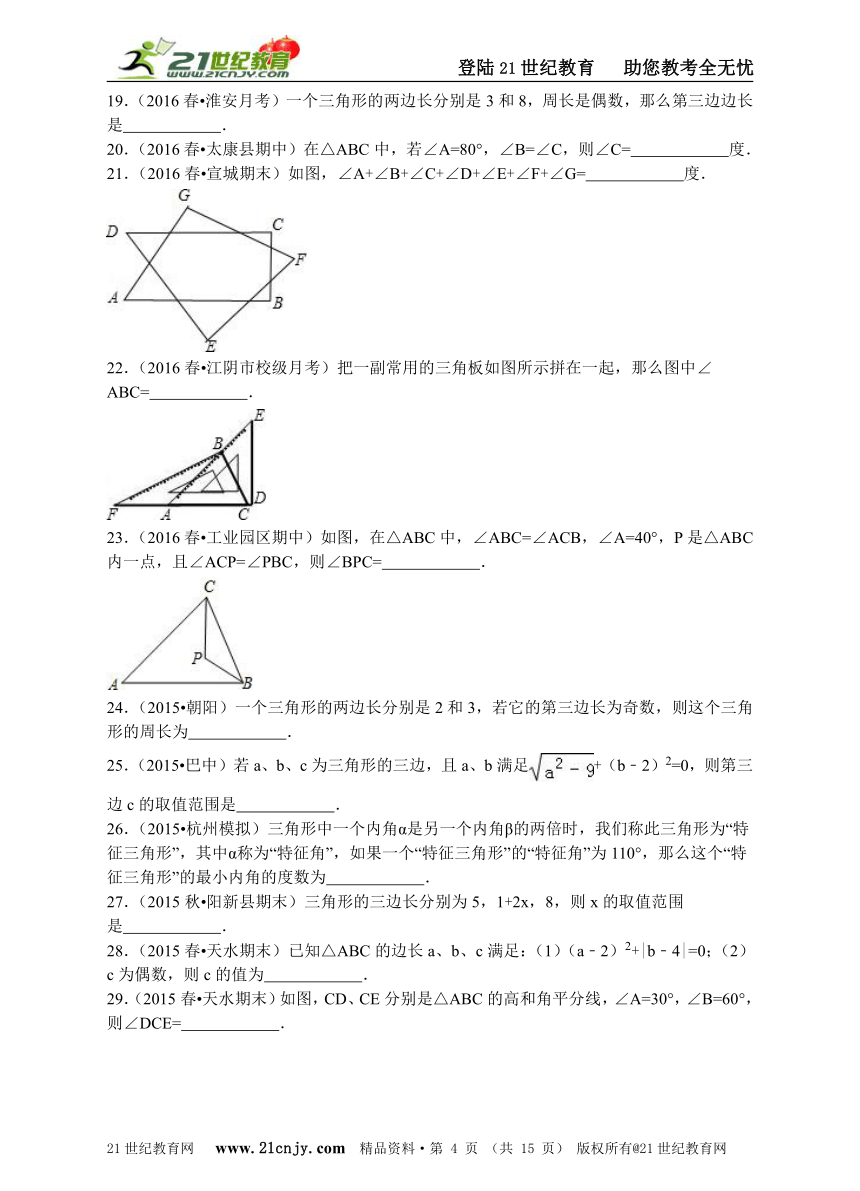
21．（2016春?宣城期末）如图，∠A+∠B+∠C+∠D+∠E+∠F+∠G=　　　　　　度．
22．（2016春?江阴市校级月考）把一副常用的三角板如图所示拼在一起，那么图中∠ABC=　　　　　　．
23．（2016春?工业园区期中）如图，在△ABC中，∠ABC=∠ACB，∠A=40°，P是△ABC内一点，且∠ACP=∠PBC，则∠BPC=　　　　　　．
24．（2015?朝阳）一个三角形的两边长分别是2和3，若它的第三边长为奇数，则这个三角形的周长为　　　　　　．
25．（2015?巴中）若a、b、c为三角形的三边，且a、b满足+（b﹣2）2=0，则第三边c的取值范围是　　　　　　．
26．（2015?杭州模拟）三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”，如果一个“特征三角形”的“特征角”为110°，那么这个“特征三角形”的最小内角的度数为　　　　　　．
27．（2015秋?阳新县期末）三角形的三边长分别为5，1+2x，8，则x的取值范围是　　　　　　．
28．（2015春?天水期末）已知△ABC的边长a、b、c满足：（1）（a﹣2）2+|b﹣4|=0；（2）c为偶数，则c的值为　　　　　　．
29．（2015春?天水期末）如图，CD、CE分别是△ABC的高和角平分线，∠A=30°，∠B=60°，则∠DCE=　　　　　　．
30．（2015春?苏州校级期末）如图所示，∠A=10°，∠ABC=90°，∠ACB=∠DCE，∠ADE=∠EDF，∠CED=∠FEG．则∠F=　　　　　　．
　

参考答案与试题解析
　
一．选择题（共12小题）
1．（2014?大庆校级模拟）三角形的三边长分别为5，8，x，则最长边x的取值范围是（　　）
A．3＜x＜8 B．5＜x＜13 C．3＜x＜13 D．8＜x＜13
【解答】解：∵5+8=13，8﹣5=3，
∴3＜x＜13，
又∵x是三角形中最长的边，
∴8＜x＜13．
故选D．
　
2．（2014秋?杭州期末）如图，在长方形网格中，每个小长方形的长为3，宽为1，A、B两点在网格格点上．若点C也在网格格点上，以A、B、C为顶点的三角形面积为3，则满足条件的点C有（　　）
A．4个 B．7个 C．9个 D．10个
【解答】解：如图，满足条件的点C共有9个．标注来的七个加C4斜右上方的两个点
故答案为：9．
　
3．（2014秋?岳池县月考）三角形中，最大角α的取值范围是（　　）
A．0°＜α＜90° B．60°＜α＜180° C．60°≤α＜90° D．60°≤α＜180°
【解答】解：根据三角形的内角和定理，又α是最大角，得：3α≥180°，即α≥60°，
故最大角α的取值范围是60°≤α＜180度．
故选D．
　
4．（2011春?江阴市校级期中）有5根小木棒，长度分别为2cm、3cm、4cm、5cm、6cm，任意取其中的3根小木棒首尾相接搭三角形，可搭出不同的三角形的个数为（　　）
A．5个 B．6个 C．7个 D．8个
【解答】解：可搭出不同的三角形为：
2cm、3cm、4cm；2cm、4cm、5cm；2cm、5cm、6cm；3cm、4cm、5cm；3cm、4cm、6cm；3cm、5cm、6cm；4cm、5cm、6cm共7个．
故选C．
　
5．（2010秋?黄州区校级期中）用五根木棒钉成如下四个图形，具有稳定性的有（　　）
A．1个 B．2个 C．3个 D．4个
【解答】解：第一个图形分成两个三角形，具有稳定性，
第二个图形根据三角形具有稳定性，左边与上边的木棒稳定，所以，另两根也稳定；
第三个图形，根据三角形具有稳定性，左边与上边的木棒稳定，所以，另两根也稳定；
第四个图形，根据三角形具有稳定性，右边与下边的木棒稳定，所以，另两根也稳定，
所以具有稳定性的有4个．
故选D．
　
6．（2009春?海安县期末）我们知道，以3根火柴为边可以组成一个三角形，那么，用6根火柴为边最多能组成（　　）个三角形．2·1·c·n·j·y
A．4 B．3 C．2 D．1
【解答】解：当用6根火柴为边组成一个正三棱椎时，此时正三棱椎有4个三角形．
故选A．
　
7．（2013?海口模拟）如图，在Rt△ADB中，∠D=90°，C为AD上一点，∠ACB=6x，则x值可以是（　　）21·世纪*教育网
A．10° B．20° C．30° D．40°
【解答】解：根据三角形的外角性质，∠ACB=6x＞90°，
解得x＞15°，
∵∠ACB是钝角，
∴6x＜180°，
∴x＜30°，
∴15°＜x＜30°，
纵观各选项，只有20°符合．
故选B．
　
8．如图，用四个螺丝将四条不可弯曲的木条围成一个木框，不计螺丝大小，其中相邻两螺丝的距离依序为2、3、4、6，且相邻两木条的夹角均可调整．若调整木条的夹角时不破坏此木框，则任两螺丝的距离之最大值为（　　）21世纪教育网版权所有
A．5 B．6 C．7 D．10
【解答】解：已知4条木棍的四边长为2、3、4、6；
①选2+3、4、6作为三角形，则三边长为5、4、6；5﹣4＜6＜5+4，能构成三角形，此时两个螺丝间的最长距离为6；21·cn·jy·com
②选3+4、6、2作为三角形，则三边长为2、7、6；6﹣2＜7＜6+2，能构成三角形，此时两个螺丝间的最大距离为7；
③选4+6、2、3作为三角形，则三边长为10、2、3；2+3＜10，不能构成三角形，此种情况不成立；
④选6+2、3、4作为三角形，则三边长为8、3、4；而3+4＜8，不能构成三角形，此种情况不成立；
综上所述，任两螺丝的距离之最大值为7．
故选：C．
　
9．7条长度均为整数厘米的线段：a1，a2，a3，a4，a5，a6，a7，满足a1＜a2＜a3＜a4＜a5＜a6＜a7，且这7条线段中的任意3条都不能构成三角形．若a1=1厘米，a7=21厘米，则a6能取的值是（　　）
A．18厘米 B．13厘米 C．8厘米 D．5厘米
【解答】解：若a1=1厘米，则后边的一个一定大于或等于前边的两个的和，则一定有：a2=2，a3=3，a4=5，a5=8，a6=13，a7=21，
故选B．
　
10．如图，△ABC绕点C按顺时针方向旋转57°后得到△DEC，如果DC⊥BC，那么∠A+∠B等于（　　）2-1-c-n-j-y
A．147° B．90° C．157° D．57°
【解答】解：∵△ABC绕点C按顺时针方向旋转57°后得到△DEC，
∴∠BCA=∠ECD，∠BCE=57°
又∵DC⊥BC，
∴∠ECD=90°﹣∠BCE=90°﹣57°=33°，
∴∠BCA=∠ECD=33°，
∴∠A+∠B=180°﹣∠BCA=180°﹣33°=147°
故选：A．
　
11．若有一条公共边的两个三角形称为一对“共边三角形”，则图中以BC为公共边的“共边三角形”有（　　）
A．2对 B．3对 C．4对 D．6对
【解答】解：△BDC与△BEC、△BDC与△BAC、△BEC与△BAC共三对．
故选：B．
　
12．为解决四个村庄用电问题，政府投资在已建电厂与这四个村庄之间架设输电线路．现已知这四个村庄及电厂之间的距离如图所示（距离单位：公里），则能把电力输送到这四个村庄的输电线路的最短总长度应该是（　　）
A．19.5 B．20.5 C．21.5 D．25.5
【解答】解：如图，最短总长度应该是：电厂到A，再从A到B、D，然后从D到C，
5+4+6+5.5=20.5km．
故选B．
　
二．填空题（共18小题）
13．（2013?宁波模拟）三条整数长度的线段不能构成三角形的总长度和的最小值为1+2+3=6，四条整数长度的线段任意三条均不能构成三角形的总长度和的最小值为1+2+3+5=11，由此请探究：一根钢管长2009cm，现把此钢管截成整数长的小钢管，使任意三根钢管均不能围成三角形，这根钢管最多可以截成　14　根整数长的小钢管．
【解答】解：1+2+3+5+8+13+21+34+55+89+144+233+377+610=1595．
所以把此钢管截成整数长的小钢管，使任意三根钢管均不能围成三角形，这根钢管最多可以截成14根整数长的小钢管．
故答案为14．
　
14．（2012?烟台）一副三角板叠在一起如图放置，最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上，BC与DE交于点M．如果∠ADF=100°，那么∠BMD为　85　度．
【解答】解：∵∠ADF=100°，∠EDF=30°，
∴∠MDB=180°﹣∠ADF﹣∠EDF=180°﹣100°﹣30°=50°，
∴∠BMD=180°﹣∠B﹣∠MDB=180°﹣45°﹣50°=85°．
故答案为：85．
　
15．（2012?犍为县模拟）某同学在纸上画了四个点，如果把这四个点彼此连接，连成一个图形，则这个图形中会有　0或3或4或8　个三角形出现．
【解答】解：∵①当四个点共线时，不能作出三角形；
②当三个点共线，第四个点不在这条直线上时，能够画出3个三角形；
③若4个点能构成凹四边形，则能画出4个三角形；
④当任意的三个点不共线时，则能够画出8个三角形．
∴0或3或4或8．
　
16．（2012?温州二模）如图，已知△ABC的面积是2平方厘米，△BCD的面积是3平方厘米，△CDE的面积是3平方厘米，△DEF的面积是4平方厘米，△EFG的面积是3平方厘米，△FGH的面积是5平方厘米，那么，△EFH的面积是　4　 平方厘米．
【解答】解：过点E作EM⊥AH，GN⊥AH，垂足分别为M，N，
∵S△AEF=S△ABC+S△BCD+S△CDE+S△DEF=2+3+3+4=12（平方厘米），
S△AGF=S△ABC+S△BCD+S△CDE+S△DEF+S△EFG=2+3+3+4+3=15（平方厘米），
∴==，
∵S△AEF=AF?EM，S△AGF=AF?NG，
∴=，
∴=，
∵S△GFH=FH?NG，S△EFH=FH?EM，
∴==，
∴S△EFH=×S△GFH=×5=4（平方厘米）；
故答案为：4．
　
17．如图，在△ABC中，点D是BC上一点，∠BAD=80°，AB=AD=DC，则∠C=　25　度．
【解答】解：∵∠BAD=80°，AB=AD=DC，
∴∠ABD=∠ADB=50°，
由三角形外角与外角性质可得∠ADC=180°﹣∠ADB=130°，
又∵AD=DC，
∴∠C=∠DAC=（180°﹣∠ADC）=25°，
∴∠C=25°．
18．（2016?端州区一模）如图，一扇窗户打开后，用窗钩BC可将其固定，这里所运用的几何原理是　三角形的稳定性　．21教育网
【解答】解：一扇窗户打开后，用窗钩BC可将其固定，这里所运用的几何原理是三角形的稳定性．
故应填：三角形的稳定性．
　
19．（2016春?淮安月考）一个三角形的两边长分别是3和8，周长是偶数，那么第三边边长是　7或9　．www.21-cn-jy.com
【解答】解：设第三边长为x，
则8﹣3＜x＜8+3，即5＜x＜11．
又∵x为奇数，
∴x=7或9，
故答案为7或9．
　
20．（2016春?太康县期中）在△ABC中，若∠A=80°，∠B=∠C，则∠C=　50　度．
【解答】解：∵∠A=80°，∠B=∠C，∠A+∠B+∠C=180°，
∴80°+2∠C=180°，
∴∠C=50°．
　
21．（2016春?宣城期末）如图，∠A+∠B+∠C+∠D+∠E+∠F+∠G=　540　度．
【解答】解：连接DG、AC．
在四边形EFGD中，得∠E+∠F+∠EDG+∠DGF=360°，
又∠1+∠2=∠3+∠4，∠5+∠6+∠B=180°，
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°．
故答案为540．
　
22．（2016春?江阴市校级月考）把一副常用的三角板如图所示拼在一起，那么图中∠ABC=　75°　．
【解答】解：∵依题可知∠ABC=180°﹣（∠BAC+∠BCA）=75°．
　
23．（2016春?工业园区期中）如图，在△ABC中，∠ABC=∠ACB，∠A=40°，P是△ABC内一点，且∠ACP=∠PBC，则∠BPC=　110°　．
【解答】解：∵∠BAC=40°，
∴∠ACB+∠ABC=180°﹣40°=140°，
又∵∠ACB=∠ABC，∠ACP=∠CBP，
∴∠PBA=∠PCB，
∴∠ACP+∠ABP=∠PCB+∠PBC=140°×=70°，
∴∠BPC=180°﹣70°=110°．
故答案为110°．
　
24．（2015?朝阳）一个三角形的两边长分别是2和3，若它的第三边长为奇数，则这个三角形的周长为　8　．【来源：21·世纪·教育·网】
【解答】解：设第三边长为x，
∵两边长分别是2和3，
∴3﹣2＜x＜3+2，
即：1＜x＜5，
∵第三边长为奇数，
∴x=3，
∴这个三角形的周长为2+3+3=8，
故答案为：8．
　
25．（2015?巴中）若a、b、c为三角形的三边，且a、b满足+（b﹣2）2=0，则第三边c的取值范围是　1＜c＜5　．21cnjy.com
【解答】解：由题意得，a2﹣9=0，b﹣2=0，
解得a=3，b=2，
∵3﹣2=1，3+2=5，
∴1＜c＜5．
故答案为：1＜c＜5．
　
26．（2015?杭州模拟）三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”，如果一个“特征三角形”的“特征角”为110°，那么这个“特征三角形”的最小内角的度数为　15°　．
【解答】解：由题意得：α=2β，α=110°，则β=55°，
180°﹣110°﹣55°=15°，
故答案为：15°．
　
27．（2015秋?阳新县期末）三角形的三边长分别为5，1+2x，8，则x的取值范围是　1＜x＜6　．
【解答】解：由题意，有8﹣5＜1+2x＜8+5，
解得：1＜x＜6．
　
28．（2015春?天水期末）已知△ABC的边长a、b、c满足：（1）（a﹣2）2+|b﹣4|=0；（2）c为偶数，则c的值为　4　．
【解答】解：∵（a﹣2）2+|b﹣4|=0，
∴a=2，b=4．
又∵a，b，c为△ABC的边长，
∴2＜c＜6．
∵c为偶数
∴c=4．
故答案为：4．
　
29．（2015春?天水期末）如图，CD、CE分别是△ABC的高和角平分线，∠A=30°，∠B=60°，则∠DCE=　15°　．21教育名师原创作品
【解答】解：∵∠A=30°，∠B=60°，
∴∠ACB=180°﹣∠A﹣∠B=90°，
∵CD、CE分别是△ABC的高和角平分线，
∴∠BCE=∠ACB=45°，∠BDC=90°，
∴∠BCD=90°﹣∠B=30°，
∴∠DCE=∠BCE﹣∠BCD=45°﹣30°=15°．
故答案为：15°．
　
30．（2015春?苏州校级期末）如图所示，∠A=10°，∠ABC=90°，∠ACB=∠DCE，∠ADE=∠EDF，∠CED=∠FEG．则∠F=　70°　．
【解答】解：在△ABC中，∠A=10°，∠ABC=90°，
在△AED中，∠FDE是它的一个外角，
∴∠FDE=∠A+∠AED，
∵∠ADE=∠EDF、
∴∠ADE=∠EDF=90°
∴∠CED=90°﹣∠A=80°
∵∠CED=∠FEG，
∴∠FEG=80°．
在△AEF中，∠FEG是它的一个外角，
∴∠FEG=∠A+∠F，
∴∠F=∠FEG﹣∠A=80°﹣10°=70°．
故答案为：70°．