浙教版八上数学2.6直角三角形 复习课件

(共19张PPT)
基础篇
1、如图，已知∠AEO=∠DCO=90o，OA=OD，
OE=OC，则∠A=∠D吗 为什么
依据:直角三角形全等有HL
2、如图，四边形ABCD中,∠B=90o，AB=4，
BC=3，CD=12，AD=13，则AC= ，
四边形ABCD的面积=
依据: 勾股定理及其逆用
5
36
勾股数
3,4,5；6,8,10；5,12,13；7,24,25；…
5
基础篇
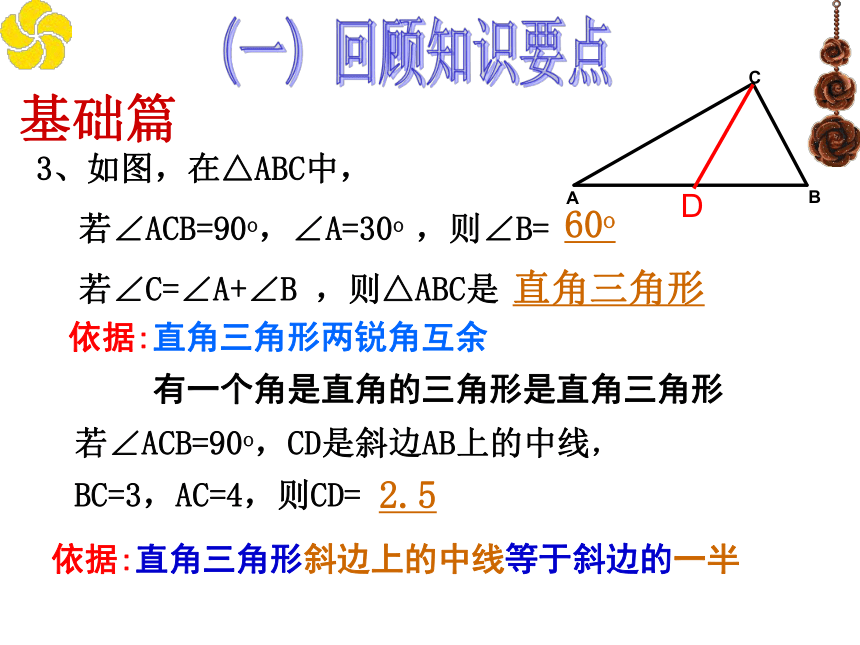
3、如图，在△ABC中，
若∠ACB=90o，∠A=30o ，则∠B=
若∠C=∠A+∠B ，则△ABC是
60o
直角三角形
依据:直角三角形两锐角互余
有一个角是直角的三角形是直角三角形
若∠ACB=90o，CD是斜边AB上的中线，
BC=3，AC=4，则CD=
依据:直角三角形斜边上的中线等于斜边的一半
2.5
基础篇
3、如图，在△ABC中，
若∠ACB=90o，∠A=30o ，则∠B=
若∠C=∠A+∠B ，则△ABC是
60o
直角三角形
若∠ACB=90o,∠A=30o，CD⊥AB，AB=4,
则BC= ，BD= ，CD=
依据: 30o角所对的直角边等于斜边的一半
2
1
若∠ACB=90o，CD是斜边AB上的中线，
BC=3，AC=4，则CD=
2.5
基础篇
四大角度看图形
角:
边:
特殊线:
两个直角三角形全等:
直角三角形两锐角互余
有一个角是直角的三角形是直角三角形
勾股定理及其逆用
直角三角形斜边上的中线等于斜边的一半
30o角所对的直角边等于斜边的一半
HL
提升篇
辩一辩
1、若一个直角三角形有两边为3、4，则斜边为5 ( )
注意1: 区分斜边是关键
2、如图，在Rt△ABC中，∠ACB=90o,AC=BC，CD为斜边AB上的高，则图中有3个等腰直角三角形 ( )
注意2: 等腰直角三角形是特殊
提升篇
辩一辩
3、如图，Rt△ABC中，∠ACB=90o，AC=4，BC=3, CD为斜边AB上的高，则CD=2.4 ( )
注意3:勾股定理常与面积法连一起
4、如图，△ABC中，D为AB的中点，
AB=6，则CD=3 ( )
注意4: 直角是前提
1、计算题
在△ABC中，已知AB=15，AC=13, BC边上的高AD=12，求:△ABC的面积
解: ∵AD⊥BC ∴∠ADB=∠ADC=90o
由勾股定理得:BD2=AB2-AD2=81，
CD2=AC2-AD2=25，∴BD=9，CD=5
∴ S△ABC 的面积=12×14÷2=84
5
9
S△ABC 的面积=12×4÷2=24
三遇分类：
体验:分类性
2、证明题
如图，已知∠ACB=∠ADB=90o，E为AB的中点，F为CD的中点，说明EF⊥CD的理由
解: 连接CE，DE，
(等腰三角形三线合一)
直角加中点,多用斜边上中线
体验:规律性
∵∠ACB=∠ADB=90o，E为AB的中点，
∴CE=0.5AB，DE=0.5AB，（？）∴CE=DE，
∵ F为CD的中点，∴ EF⊥CD
3、探究题
解: 设EC为x，则
体验:实践性
DE=8-x，EF=8-x，AF=10，
由勾股定理得:BF=6，∴FC=4，
由勾股定理得: X2+16=(8-x)2
∴ x=3
如图，折叠长方形（对边相等，每个角都是直角）的一边，使点D落在BC边上的一点F处。
已知AB=8，BC=10，求 EC的长
把一副三角板按如图方式放置，则两条斜边所成的钝角 =____度。
30o
45o
165o
4、操作题
一副三角板叠放在一起，如图所示，若BD=4；求AB的长？
A
B
D
E
C
求AC的长？
设AC=BC=x，∴x2+x2=12，∴x=
在△ABC中，AC=BC，∠C=90o，将一块三角板的直角顶点放在斜边AB的中点P处，如图（1）（2）将三角板绕P点旋转，三角板的两直角边分别交射线AC、CB于D、E两点。 (1)猜想PD与PE有何大小关系？
(2)并以图(2)为例说明理由；
(３)在旋转过程中，还会存在与图(1)、(2)不同的情形吗？若存在，请在图(3)中画出，并加以说明。
A
C
B
P
D
E
A
C
B
P
D
E
(1)
(3)
A
C
B
P
D
E
体验:拓展性
(2)
理一理
发现了……
学会了……
你知道了……
回顾篇
①角 ②边
③特殊线 ④两个Rt△全等
分类性 规律性 实践性 拓展性
四大角度
四个注意
四种体验
区分斜边是关键、等腰直角三角形是特殊、勾股定理常与面积法连一起、最后直角是前提
作业:
一分耕耘，一分收获，相信自己，付出总会有回报。努力吧，成功就在你眼前。
一块含30o角的直角三角板（如图），它的斜边AB=8cm，里面空心△DEF的各边与△ABC的对应边平行，且各对应边的距离都是1cm，求FD的长？
C
A
B
D
E
F
M
N
G
H
返回
如图1，△ABC放置在另一块直角三角板XYZ上，恰好三角板XYZ的两条直角边XY，XZ分别经过点B，C,且BC∥YZ.则∠XBC+∠XCB=___， ∠ABX=____;
B
Y
C
B
Y
Z
A
X
图(1)
图(2)
90o
15o
A
C
Z
X
Y
B
如图2，改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY，XZ仍然经过点B，C。那么∠ABX+∠ACX的大小是否变化 若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
体验:拓展性
如图，折叠长方形（对边相等，每个角都是直角）的一边，使点D落在BC边上的一点F处。已知AB=8,BC=10,求 EC的长
如图，△ABC中，∠C=90°,AC=5,AB=13,
折叠AC，使点C落在AB边上的一点D，
求CE 的长。
A
D
C
B
E