浙教版数学九上1.3二次函数性质 课件 (共20张PPT)
文档属性
| 名称 | 浙教版数学九上1.3二次函数性质 课件 (共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 460.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-05 20:07:04 | ||
图片预览





文档简介
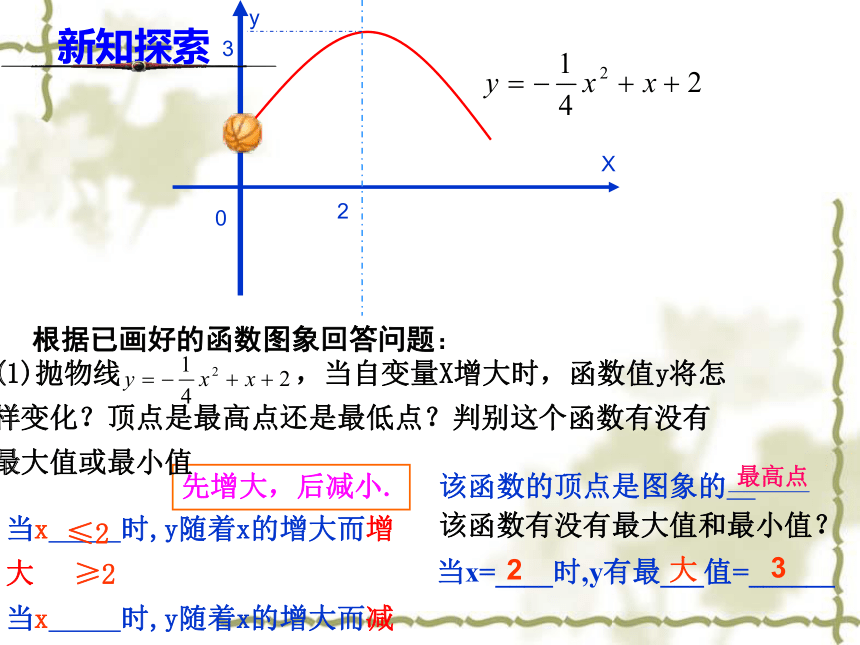
课件20张PPT。运动员投篮时,篮球运动的路线是怎样的一条曲线?怎样计算篮球达到最高点时的高度?你知道他是谁吗?新知探索根据已画好的函数图象回答问题:先增大,后减小.当x 时,y随着x的增大而增大
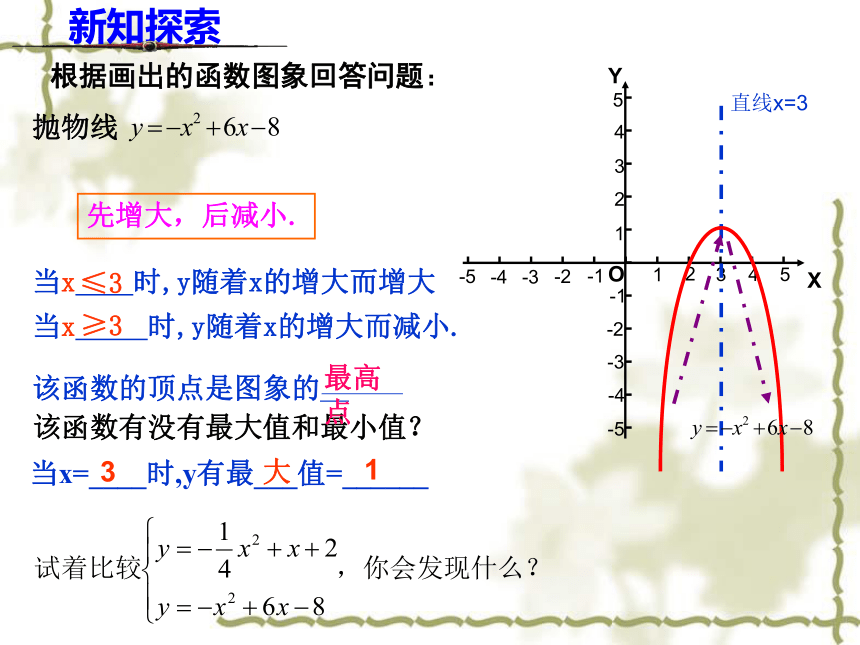
当x 时,y随着x的增大而减小.≤2≥2(1)抛物线 ,当自变量X增大时,函数值y将怎样变化?顶点是最高点还是最低点?判别这个函数有没有最大值或最小值该函数有没有最大值和最小值?当x=____时,y有最___值=______2大3 最高点根据画出的函数图象回答问题:抛物线 先增大,后减小.当x 时,y随着x的增大而增大
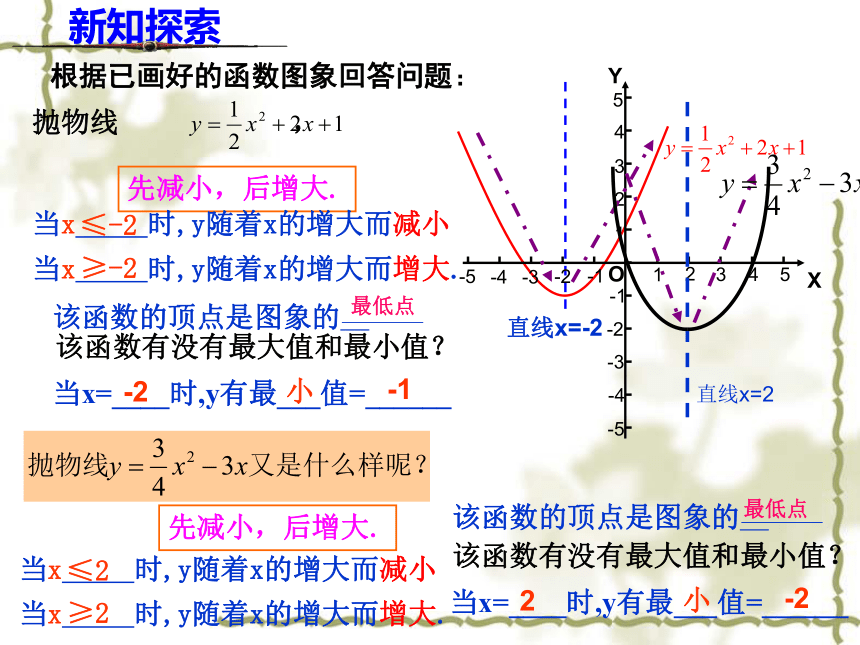
当x 时,y随着x的增大而减小.≤3 ≥3新知探索该函数有没有最大值和最小值?当x=____时,y有最___值=______3大1直线x=3最高点根据已画好的函数图象回答问题:抛物线 ,先减小,后增大.当x 时,y随着x的增大而减小
当x 时,y随着x的增大而增大.≤-2≥-2新知探索直线x=-2先减小,后增大.当x 时,y随着x的增大而减小
当x 时,y随着x的增大而增大.≤2≥2该函数有没有最大值和最小值?当x=____时,y有最___值=______-2小-1该函数有没有最大值和最小值?当x=____时,y有最___值=______2小-2最低点直线x=2最低点
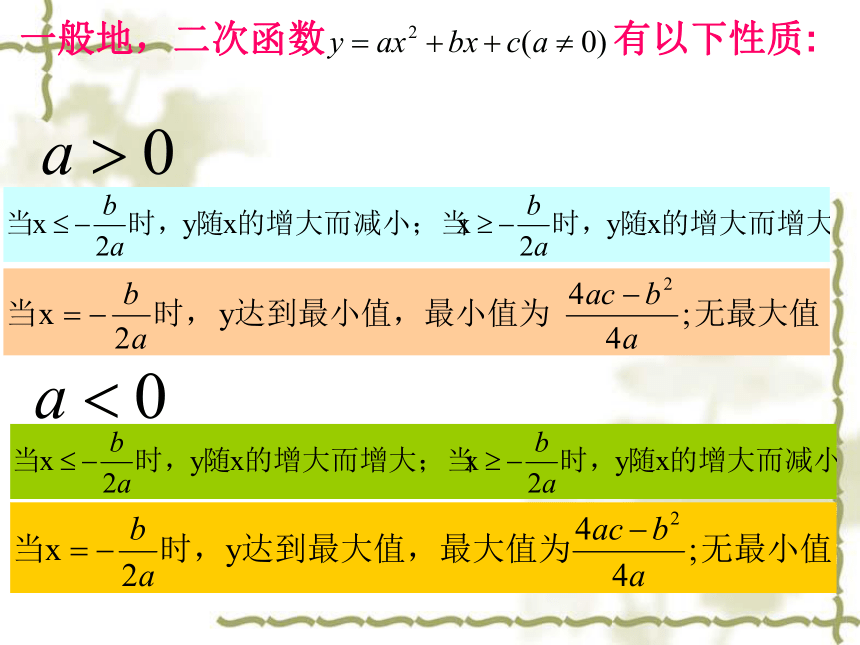
一般地,二次函数 有以下性质: 例1:已知下列函数:
①求出函数对称轴和顶点坐标;
②说出函数的增减性;
③当x为何值时有最大值(或最小值),并求出最大值或最小值。
(1)
(2)新知运用新知探索二次函数 y=ax2+bx+c一元二次方程 ax2+bx+c=0思考若令y=0,则变成了求二次函数y=x2+2x图象与x轴的交点。解:∵与x轴的交点的纵坐标为0,
∴令y=0,则x2+2x=0
解得:x1=0,x2=-2;
∴二次函数y=x2+2x图象与
x轴有两个交点(0,0) , (-2,0)则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A( ), B( )x1,0x2,0x抛物线y=ax2+bx+c与x轴的交点若一元二次方程ax2+bx+c=0的两个根是x1,x2,ax2+bx+c=02个1个0个b2- 4ac
=(-1)2-4x2x(-1)
=9﹥0b2- 4ac=0b2- 4ac=-56<0有两个交点b2-4ac > 0有一个交点b2-4ac = 0没有交点b2-4ac < 0你能画出y=2x2+3x+1 这个函数的大致图象吗?结合顶点,对称轴,与y轴交点,顶点:
对称轴:
与y轴交点:
与X轴交点:直线 x=自变量x在什么范围内时, y随着x的增大而增大?何时y随着x的增大而减少;并求出函数的最大值或最小值。与X轴交点模拟情景湖人VS火箭VS解: ⑴设函数解析式为:
y=a(x-2.5)2+k,根据题意,得:则:a=-0.2,k=3.5∴解析式为:y=-0.2x2+x+2.25,
自变量x的取值范围为:0≤x≤4.⑵球在运动中离地面的最大
高度为3.5米。篮球运动员投篮时,球运动的路线为抛物线的一部分(3)姚明双手举起的高度是2.95m,在科比前1m处,不跳起的情况,姚明能碰到科比投出的篮球吗?(4)姚明双手举起的高度是2.95m,在科比前1m处,
应跳起多少高度,姚明才能碰到科比投出的篮球吗?篮球运动员投篮时,球运动的路线为抛物线的一部分(如图),抛物线的对称轴为x=2.5。
求:
⑴球运动路线的函数解析式和自变量的取值范围;
⑵球在运动中离地面的最大高度。
(3)姚明双手举起的高度是2.95m,在
科比前1m处,不跳起的情况,姚
明能碰到科比投出的篮球吗?
(4)姚明双手举起的高度是
2.95m,在科比前1m处,
应跳起多少高度,姚明才能
碰到科比投出的篮球吗?
题
目
回
顾总结1,抓住本质与特点
2,化繁为简,化整为零,个个击破。作业:相应的配套练习。
当x 时,y随着x的增大而减小.≤2≥2(1)抛物线 ,当自变量X增大时,函数值y将怎样变化?顶点是最高点还是最低点?判别这个函数有没有最大值或最小值该函数有没有最大值和最小值?当x=____时,y有最___值=______2大3 最高点根据画出的函数图象回答问题:抛物线 先增大,后减小.当x 时,y随着x的增大而增大
当x 时,y随着x的增大而减小.≤3 ≥3新知探索该函数有没有最大值和最小值?当x=____时,y有最___值=______3大1直线x=3最高点根据已画好的函数图象回答问题:抛物线 ,先减小,后增大.当x 时,y随着x的增大而减小
当x 时,y随着x的增大而增大.≤-2≥-2新知探索直线x=-2先减小,后增大.当x 时,y随着x的增大而减小
当x 时,y随着x的增大而增大.≤2≥2该函数有没有最大值和最小值?当x=____时,y有最___值=______-2小-1该函数有没有最大值和最小值?当x=____时,y有最___值=______2小-2最低点直线x=2最低点
一般地,二次函数 有以下性质: 例1:已知下列函数:
①求出函数对称轴和顶点坐标;
②说出函数的增减性;
③当x为何值时有最大值(或最小值),并求出最大值或最小值。
(1)
(2)新知运用新知探索二次函数 y=ax2+bx+c一元二次方程 ax2+bx+c=0思考若令y=0,则变成了求二次函数y=x2+2x图象与x轴的交点。解:∵与x轴的交点的纵坐标为0,
∴令y=0,则x2+2x=0
解得:x1=0,x2=-2;
∴二次函数y=x2+2x图象与
x轴有两个交点(0,0) , (-2,0)则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A( ), B( )x1,0x2,0x抛物线y=ax2+bx+c与x轴的交点若一元二次方程ax2+bx+c=0的两个根是x1,x2,ax2+bx+c=02个1个0个b2- 4ac
=(-1)2-4x2x(-1)
=9﹥0b2- 4ac=0b2- 4ac=-56<0有两个交点b2-4ac > 0有一个交点b2-4ac = 0没有交点b2-4ac < 0你能画出y=2x2+3x+1 这个函数的大致图象吗?结合顶点,对称轴,与y轴交点,顶点:
对称轴:
与y轴交点:
与X轴交点:直线 x=自变量x在什么范围内时, y随着x的增大而增大?何时y随着x的增大而减少;并求出函数的最大值或最小值。与X轴交点模拟情景湖人VS火箭VS解: ⑴设函数解析式为:
y=a(x-2.5)2+k,根据题意,得:则:a=-0.2,k=3.5∴解析式为:y=-0.2x2+x+2.25,
自变量x的取值范围为:0≤x≤4.⑵球在运动中离地面的最大
高度为3.5米。篮球运动员投篮时,球运动的路线为抛物线的一部分(3)姚明双手举起的高度是2.95m,在科比前1m处,不跳起的情况,姚明能碰到科比投出的篮球吗?(4)姚明双手举起的高度是2.95m,在科比前1m处,
应跳起多少高度,姚明才能碰到科比投出的篮球吗?篮球运动员投篮时,球运动的路线为抛物线的一部分(如图),抛物线的对称轴为x=2.5。
求:
⑴球运动路线的函数解析式和自变量的取值范围;
⑵球在运动中离地面的最大高度。
(3)姚明双手举起的高度是2.95m,在
科比前1m处,不跳起的情况,姚
明能碰到科比投出的篮球吗?
(4)姚明双手举起的高度是
2.95m,在科比前1m处,
应跳起多少高度,姚明才能
碰到科比投出的篮球吗?
题
目
回
顾总结1,抓住本质与特点
2,化繁为简,化整为零,个个击破。作业:相应的配套练习。
同课章节目录
