3.2 图形的旋转 同步练习（含答案）

3.2
图形的旋转
同步练习
【练习1】
一、填空题．
1．如图所示，△ABC的∠BAC=90°，AB=AC=5cm．△ABC
按逆时针方向转动一个角度后成为△ACD，则图中________是旋转中心，旋转_______度，点B与点_____是对应点，点C与点______是对应点，∠ACD=______，AD=________．
( http: / / www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
)
2．如图，E为正方形ABCD内一点，∠AEB=135°，BE=3cm，△AEB按顺时针方向旋转一个角度后成为△CFB，图中_______是旋转中心，旋转_______度，
点A
与点_________是对应点，点E与点________是对应点，△BEF是______三角形，∠CBF=
∠______，∠BFC=________度，∠EFC=_______度，BF=______cm．
( http: / / www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
)
3．如图所示，△ABC、△ADE均是顶角为42°的等腰三角形，BC和DE
分别是底边，图中△______与△_______，可以通过以点________为旋转中心，旋转角度为________，其中∠BAD=∠________，CE=_______．
( http: / / www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
)
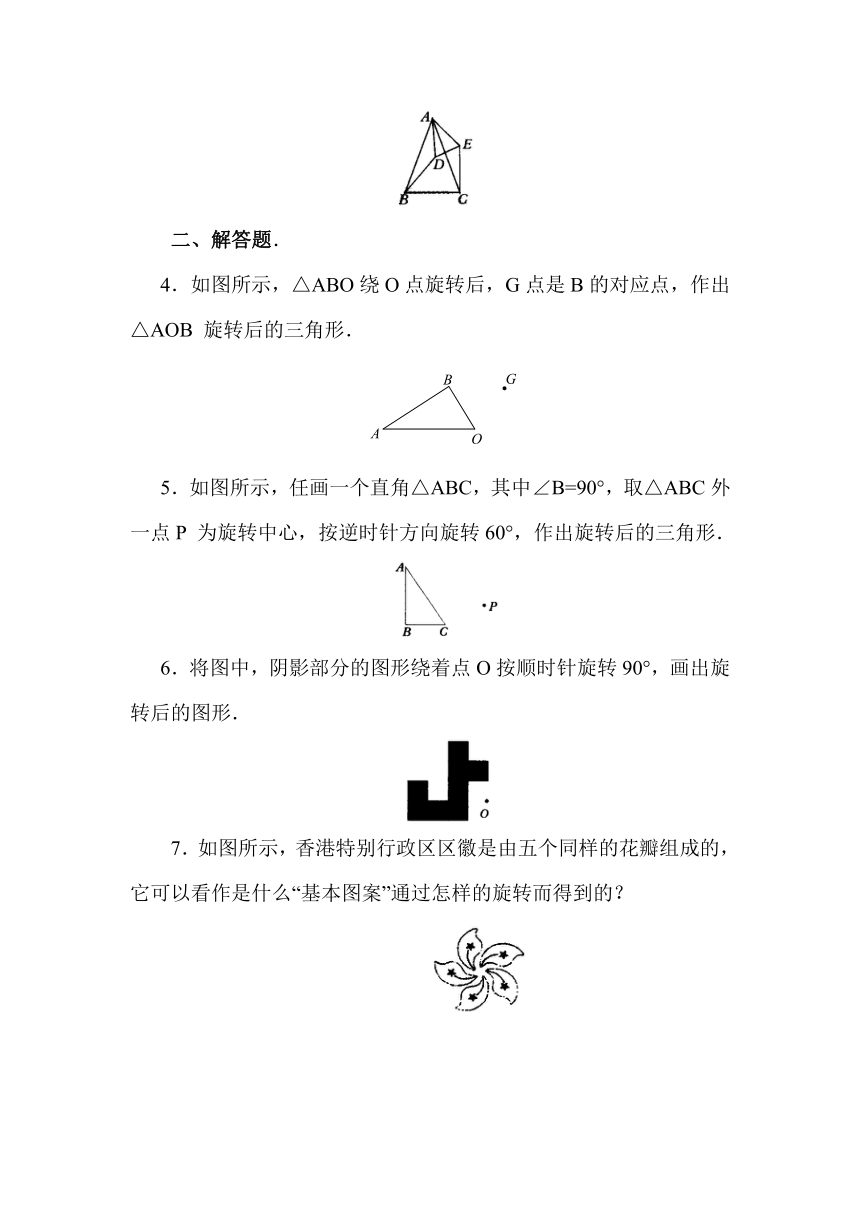
二、解答题．
4．如图所示，△ABO绕O点旋转后，G点是B的对应点，作出△AOB
旋转后的三角形．
( http: / / www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
)
5．如图所示，任画一个直角△ABC，其中∠B=90°，取△ABC外一点P
为旋转中心，按逆时针方向旋转60°，作出旋转后的三角形．
( http: / / www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
)
6．将图中，阴影部分的图形绕着点O按顺时针旋转90°，画出旋转后的图形．
( http: / / www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
)
7．如图所示，香港特别行政区区徽是由五个同样的花瓣组成的，
它可以看作是什么“基本图案”通过怎样的旋转而得到的？
( http: / / www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
)
【练习1】参考答案
一、1．A
90
C
D
∠B
AC
2．B
90
C
F
等腰三角形
∠ABE（AEB）
135
90
3cm
3．ABD
ACE
A
42°
∠CAE
BD
二、4．略
5．
先找到图案中的关键点
把关键点绕着O按顺时针方向转动60°，得到它各自的对应点，
即可获得旋转后的图形．
6～7．略
【练习2】
◆基础检测
1、如图,过圆心O和圆上一点A连一条曲线,将曲线OA绕O点按同一方向连续旋转三次,每次旋转90°,把圆分成四部分,则（
）
A．这四部分不一定相等
B．这四部分相等
B．前一部分小于后一部分
D．不能确
2、如图是一个旋转对称图形，要使它旋转后与自身重合，至少应将它绕中心逆时针方向旋转的度数为（
）
A．30°
B．60°
C．120°
D．180°
3、如图所示的图形是旋转对称图形，它是绕它的旋转中心旋转_______度后与自身重合的？
4、如图所示的五角星绕中心点旋转一定的角度后能与自身完全重合，则其旋转的角度至少为
5、如上图案可以看做是哪个基本图形通过几次旋转得到的？每次旋转了多少度？旋转中心是哪个？
◆典例分析
我们在生活中可以看到不少图形绕着某一点旋转一定的角度后重合，如下图所示，这四个图形都是旋转对称图形．
⑴
⑵
⑶
⑷
请大家观察上面的图形，然后说一说它们在旋转多少度后能与自身重合？
解：
图（1）绕着一点旋转180°后能与自身重合．
图（2）绕着一点旋转120°或240°后能与自身重合．
图（3）绕着一点旋转90°或180°或270°后能与自身重合．
图（4）绕着一点旋转72°划144°或216°或288°后能与自身重合．
●拓展提高
1、如下四个图案，它们绕中心旋转一定的度数后都能和原来的图形相互重合，其中有一个图案与其余图案旋转的度数不同的是（　　）
（A）　　　（B）　　　（C）　　　（D）
2、如图所示图形旋转一定角度能与自身重合，则旋转的角度可能是
（
）
A．30°
B．60°
C．90°
D．120°
3、如图所示的图案是由两个边长相等的正方形组成的，把这个图案旋转一定角度后可以与原来的图案重合，则旋转的角度为（
）
A．45°或90°
B．90°或180°
C．180°或270°
D．n·45°（1≤n≤8，且n为正整数）
4、如图，已知等边三角形ABC和等边三角形DBC有公共的底边BC，以图中的某个点为旋转中心，旋转△DBC与△ABC重合，则旋转中心为
（写出所有满足条件的点）．
HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
"
5、如图，是某设计师设计的方桌布图案的一部分，请你运用旋转的方法，将该图案绕原点O顺时针依次旋转90°、180°、270°，并画出图形，你来试一试吧！但是涂阴影时，要注意利用旋转变换的特点，不要涂错了位置，否则你将得不到理想的效果，并且还要扣分的噢！
( http: / / www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
)
6、已知如图，正方形ABCD中，E为CD边上一点，F为BC边上一点，CE=CF:
（1）HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
"相等吗？
（2）△DCF能与△BCE重合吗？
（3）BE与DF垂直吗？
SHAPE
\
MERGEFORMAT
( http: / / www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
)
●体验中考
1、如图，△ABC的直角三角形，BC是斜边，将△ABP绕点A逆时针旋转后，能与△ACP′重合，如果AP=3，求PP′的长．
【练习2】参考答案
◆基础检测
1、B.旋转对称图形:绕着某电脑旋转一定的角度与自身重合，本题是旋转HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
"
2、B如果一幅旋转对称图形有n个图案，那么这个图形至少旋转HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
"倍后，能与自身重合，即旋转HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
"倍后都能与自身重合．本题至少旋转HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
"
3、HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
"
图形旋转HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
"倍后，均能与自身重合．
4、HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
".
HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
"
5、
本题图案可以看作由一个菱形通过6次旋转得到的，每次旋转HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
"，旋转中心在图形的中心．
●拓展提高
1、B.
A、C、D都是旋转HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
"与自身重合，而B旋转HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
"与自身重合．
2、C
HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
"
3、D
4、B、C、BC的中点
5、基本图形是其中一个菱形，通过5次旋转得到．每次旋转了60度，旋转中心是整个图案的中心．
6、解：∵CE=CF,BC=CD,∠DCF=∠DCB=90°,∴△DCF可看作由△BCE以点C为旋转中心顺时针旋转90°得到的，所以（1）HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
"，（2）△DCF能与△BCE重合
（3）延长BE交DF于点G,∵HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
"，HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
"
在△BEG中，HYPERLINK
"http://www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
"
即BE⊥DF
●体验中考
1、∵△ABP绕点A逆时针旋转后，能与△ACP′重合，
∴AP′=AP，∠CAP′=∠BAP，
∴∠PAP′=∠PAC+∠CAP′=∠PAC+∠BAP=∠BAC=90°，
△PAP′为等腰直角三角形，PP′为斜边，
∴PP′=
( http: / / www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
)AP=3
( http: / / www.21cnjy.com"
\o
"欢迎登陆21世纪教育网"
)．
A