1.3证明同步练习

1.3证明同步练习
一．选择题（共15小题）
1．（2015秋?鄂州校级月考）如图游戏：人从格外只能进入第1格，在格中，每次可向前跳1格或2格，那么人从格外跳到第6格可以有（　　）种方法．【来源：21·世纪·教育·网】
A．6 B．7 C．8 D．9
2．（2016?湖州）如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若AD=8，则点P到BC的距离是（　　）【出处：21教育名师】
A．8 B．6 C．4 D．2
3．（2016?铜仁市）如图，已知∠AOB=30°，P是∠AOB平分线上一点，CP∥OB，交OA于点C，PD⊥OB，垂足为点D，且PC=4，则PD等于（　　）【版权所有：21教育】
A．1 B．2 C．4 D．8
4．（2016?怀化）如图，OP为∠AOB的角平分线，PC⊥OA，PD⊥OB，垂足分别是C、D，则下列结论错误的是（　　）
A．PC=PD B．∠CPD=∠DOP C．∠CPO=∠DPO D．OC=OD
5．（2016?枣庄）如图，在△ABC中，AB=AC，∠A=30°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D的度数为（　　）
A．15° B．17.5° C．20° D．22.5°
6．（2016?厦门校级模拟）如图，OP是∠AOB的平分线，点P到OA的距离为3，点N是OB上的任意一点，则线段PN的取值范围为（　　）
A．PN＜3 B．PN＞3 C．PN≥3 D．PN≤3
7．（2016?惠安县二模）已知Rt△ABC中，∠C=90°，AC=3，BC=4，AD平分∠BAC，则点B到AD的距离是（　　）
A． B．2 C． D．
8．如图，AB∥CD，AC⊥BC，图中与∠CAB互余的角有（　　）
A．1个 B．2个 C．3个 D．0个
9．（2010?肇庆）如图所示，已知AB∥CD，∠A=50°，∠C=∠E．则∠C等于（　　）
A．20° B．25° C．30° D．40°
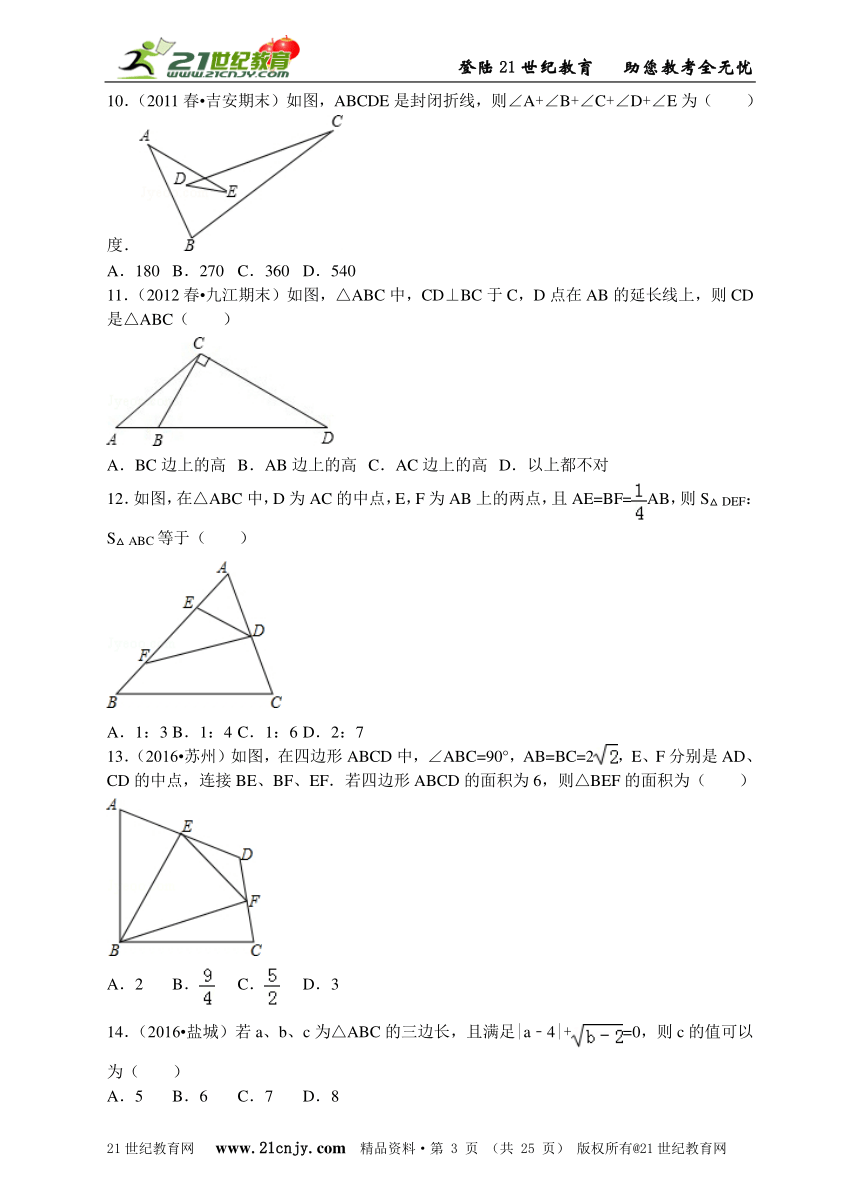
10．（2011春?吉安期末）如图，ABCDE是封闭折线，则∠A+∠B+∠C+∠D+∠E为（　　）度．
A．180 B．270 C．360 D．540
11．（2012春?九江期末）如图，△ABC中，CD⊥BC于C，D点在AB的延长线上，则CD是△ABC（　　）
A．BC边上的高 B．AB边上的高 C．AC边上的高 D．以上都不对
12．如图，在△ABC中，D为AC的中点，E，F为AB上的两点，且AE=BF=AB，则S△DEF：S△ABC等于（　　）
A．1：3 B．1：4 C．1：6 D．2：7
13．（2016?苏州）如图，在四边形ABCD中，∠ABC=90°，AB=BC=2，E、F分别是AD、CD的中点，连接BE、BF、EF．若四边形ABCD的面积为6，则△BEF的面积为（　　）
A．2 B． C． D．3
14．（2016?盐城）若a、b、c为△ABC的三边长，且满足|a﹣4|+=0，则c的值可以为（　　）
A．5 B．6 C．7 D．8
15．（2015?东西湖区校级模拟）如图，∠EOF内有一定点P，过点P的一条直线分别交射线OE于A，射线OF于B．当满足下列哪个条件时，△AOB的面积一定最小（　　）
A．OA=OB B．OP为△AOB的角平分线
C．OP为△AOB的高 D．OP为△AOB的中线
　
二．填空题（共1小题）
16．（2006?烟台）如图，三角形纸片ABC中，∠A=65°，∠B=75°，将纸片的一角折叠，使点C落在△ABC内，若∠1=20°，则∠2的度数为　　　　　　度．
　
三．解答题（共14小题）
17．（2015春?邢台校级期末）如图，已知AB∥CD，∠B=120°，∠C=25°，求∠E．
18．（2014春?南京期末）看图填空：
已知：如图，AD⊥BC于D，EF⊥BC于F，交AB于G，交CA延长线于E，∠1=∠2．求证：AD平分∠BAC．
证明：∵AD⊥BC，EF⊥BC（已知）
∴∠ADC=90°，∠EFC=90°（垂线的定义）
∴　　　　　　=　　　　　　
　　　　　　∥　　　　　　
∴∠1=　　　　　　
∠2=　　　　　　
∵∠1=∠2（已知）
∴　　　　　　
∴AD平分∠BAC（角平分线定义）
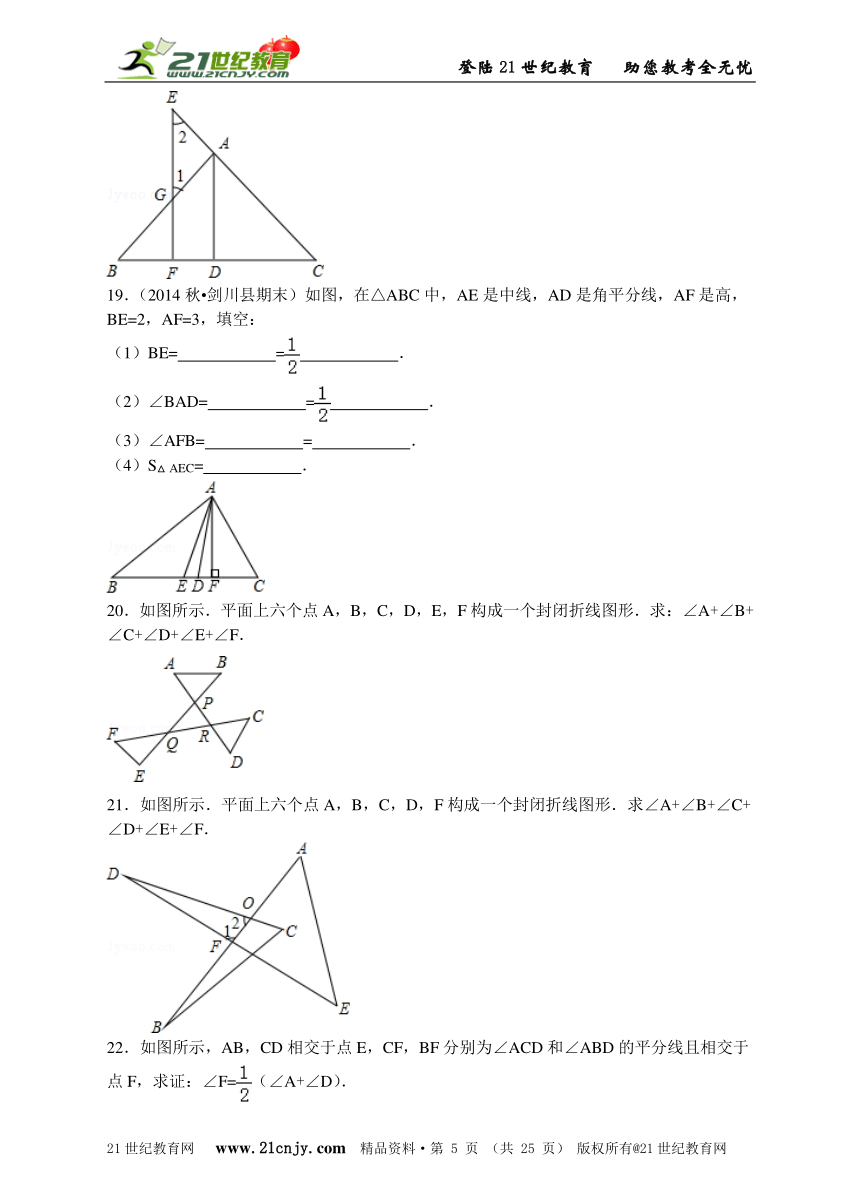
19．（2014秋?剑川县期末）如图，在△ABC中，AE是中线，AD是角平分线，AF是高，BE=2，AF=3，填空：
（1）BE=　　　　　　=　　　　　　．
（2）∠BAD=　　　　　　=　　　　　　．
（3）∠AFB=　　　　　　=　　　　　　．
（4）S△AEC=　　　　　　．
20．如图所示．平面上六个点A，B，C，D，E，F构成一个封闭折线图形．求：∠A+∠B+∠C+∠D+∠E+∠F．
21．如图所示．平面上六个点A，B，C，D，F构成一个封闭折线图形．求∠A+∠B+∠C+∠D+∠E+∠F．
22．如图所示，AB，CD相交于点E，CF，BF分别为∠ACD和∠ABD的平分线且相交于点F，求证：∠F=（∠A+∠D）．
23．（2016春?高密市期末）如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠CAB=50°，∠C=60°，求∠DAE和∠BOA的度数．
24．（2016春?故城县期末）如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=30°．求：
（1）∠BAE的度数；
（2）∠DAE的度数；
（3）探究：小明认为如果条件∠B=70°，∠C=30°改成∠B﹣∠C=40°，也能得出∠DAE的度数？若能，请你写出求解过程；若不能，请说明理由．
25．（2016春?淮安期中）在△ABC中，CD⊥AB于D，CE是∠ACB的平分线，∠A=20°，∠B=60°．求∠BCD和∠ECD的度数．
26．（2016春?江苏月考）我们知道，任何一个三角形的三条内角平分线相交于一点，如图，若△ABC 的三条内角平分线相交于点I，过I作DE⊥AI分别交AB、AC于点D、E．
（1）请你通过画图、度量，填写右上表（图画在草稿纸上，并尽量画准确）
（2）从上表中你发现了∠BIC与∠BDI之间有何数量关系，请写出来，并说明其中的道理．
∠BAC的度数
40°
60°
90°
120°
∠BIC的度数
∠BDI的度数
27．（2015秋?全椒县期中）已知△ABC中，∠ACB=90°，CD为AB边上的高，BE平分∠ABC，分别交CD、AC于点F、E，求证：∠CFE=∠CEF．www-2-1-cnjy-com
28．（2015秋?泰兴市校级期中）（1）如图（1），已知，在△ABC中，AD，AE分别是△ABC的高和角平分线，若∠B=30°，∠C=50°．求∠DAE的度数；21*cnjy*com
（2）如图（2），已知AF平分∠BAC，交边BC于点E，过F作FD⊥BC，若∠B=x°，∠C=（x+36）°，
①∠CAE=　　　　　　（含x的代数式表示）
②求∠F的度数．
29．（2013春?唐山期末）△ABC中，AD⊥BC，AE平分∠BAC交BC于点E．
（1）∠B=30°，∠C=70°，求∠EAD的大小．
（2）若∠B＜∠C，则2∠EAD与∠C﹣∠B是否相等？若相等，请说明理由．
　

1.3证明同步练习
参考答案与试题解析
　
一．选择题（共15小题）
1．（2015秋?鄂州校级月考）如图游戏：人从格外只能进入第1格，在格中，每次可向前跳1格或2格，那么人从格外跳到第6格可以有（　　）种方法．
A．6 B．7 C．8 D．9
【解答】解：每次向前跳l格，有唯一的跳法；
仅有一次跳2格，其余每次向前跳l格，有4种的跳法；
有两次跳2格，其余每次向前跳l格，有3种的跳法．
则共有1+4+3=8种．
故选：C．
　
2．（2016?湖州）如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若AD=8，则点P到BC的距离是（　　）
A．8 B．6 C．4 D．2
【解答】解：过点P作PE⊥BC于E，
∵AB∥CD，PA⊥AB，
∴PD⊥CD，
∵BP和CP分别平分∠ABC和∠DCB，
∴PA=PE，PD=PE，
∴PE=PA=PD，
∵PA+PD=AD=8，
∴PA=PD=4，
∴PE=4．
故选C．
　
3．（2016?铜仁市）如图，已知∠AOB=30°，P是∠AOB平分线上一点，CP∥OB，交OA于点C，PD⊥OB，垂足为点D，且PC=4，则PD等于（　　）
A．1 B．2 C．4 D．8
【解答】解：作PE⊥OA于E，如图，
∵CP∥OB，
∴∠ECP=∠AOB=30°，
在Rt△EPC中，PE=PC=×4=2，
∵P是∠AOB平分线上一点，PE⊥OA，PD⊥OB，
∴PD=PE=2．
故选B．
　
4．（2016?怀化）如图，OP为∠AOB的角平分线，PC⊥OA，PD⊥OB，垂足分别是C、D，则下列结论错误的是（　　）2-1-c-n-j-y
A．PC=PD B．∠CPD=∠DOP C．∠CPO=∠DPO D．OC=OD
【解答】解：∵OP为∠AOB的角平分线，PC⊥OA，PD⊥OB，垂足分别是C、D，
∴PC=PD，故A正确；
在Rt△OCP与Rt△ODP中，
，
∴△OCP≌△ODP，
∴∠CPO=∠DPO，OC=OD，故C、D正确．
不能得出∠CPD=∠DOP，故B错误．
故选B．
　
5．（2016?枣庄）如图，在△ABC中，AB=AC，∠A=30°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D的度数为（　　）21教育名师原创作品
A．15° B．17.5° C．20° D．22.5°
【解答】解：∵∠ABC的平分线与∠ACE的平分线交于点D，
∴∠1=∠2，∠3=∠4，
∵∠ACE=∠A+∠ABC，
即∠1+∠2=∠3+∠4+∠A，
∴2∠1=2∠3+∠A，
∵∠1=∠3+∠D，
∴∠D=∠A=×30°=15°．
故选A．
　
6．（2016?厦门校级模拟）如图，OP是∠AOB的平分线，点P到OA的距离为3，点N是OB上的任意一点，则线段PN的取值范围为（　　）
A．PN＜3 B．PN＞3 C．PN≥3 D．PN≤3
【解答】解：作PM⊥OB于M，
∵OP是∠AOB的平分线，PE⊥OA，PM⊥OB，
∴PM=PE=3，
∴PN≥3，
故选：C．
　
7．（2016?惠安县二模）已知Rt△ABC中，∠C=90°，AC=3，BC=4，AD平分∠BAC，则点B到AD的距离是（　　）
A． B．2 C． D．
【解答】解：过点D作DE⊥AB交AB于E，
∵∠C=90°，AC=3，BC=4，
∴AB==5，
设CD=x，则BD=8﹣x，
∵AD平分∠BAC，
∴=，即=，
解得，x=
∴CD=，
∴S△ABD=×AB?DE=×5=，
∵AD==，
设BD到AD的距离是h，
∴S△ABD=×AD?h，
∴h=．
故选：C．
　
8．如图，AB∥CD，AC⊥BC，图中与∠CAB互余的角有（　　）
A．1个 B．2个 C．3个 D．0个
【解答】解：∵AB∥CD，
∴∠CBA=∠BCD，
∵AC⊥BC，
∴∠ACB=90°，
∴∠CAB+∠CBA=90°，
∴∠CAB+∠BCD=90°，
即图中与∠CAB互余的角有∠CBA和∠BCD两个．
故选B．
　
9．（2010?肇庆）如图所示，已知AB∥CD，∠A=50°，∠C=∠E．则∠C等于（　　）
A．20° B．25° C．30° D．40°
【解答】解：∵AB∥CD，∠A=50°，
∴∠A=∠AOC（内错角相等），
又∵∠C=∠E，∠AOC是外角，
∴∠C=50°÷2=25°．
故选B．
　
10．（2011春?吉安期末）如图，ABCDE是封闭折线，则∠A+∠B+∠C+∠D+∠E为（　　）度．
A．180 B．270 C．360 D．540
【解答】解：连接AC．
根据三角形的内角和定理，得
∠D+∠E=∠CAE+∠ACD．
∴∠A+∠B+∠C+∠D+∠E=∠B+∠BAC+∠ACB=180°．
故选A．
　
11．（2012春?九江期末）如图，△ABC中，CD⊥BC于C，D点在AB的延长线上，则CD是△ABC（　　）
A．BC边上的高 B．AB边上的高 C．AC边上的高 D．以上都不对
【解答】解：CD是△BCD中BC边上的高，而不是△ABC的高．
故选D．
　
12．如图，在△ABC中，D为AC的中点，E，F为AB上的两点，且AE=BF=AB，则S△DEF：S△ABC等于（　　）
A．1：3 B．1：4 C．1：6 D．2：7
【解答】解：分别过点C、D作CG⊥AB，DK⊥AB，垂足分别为G、K，
∵AE=BF=AB，
∴FK=AB．
∵D为AC的中点，
∴DK=CG，
∴S△DEF：S△ABC====1：4．
故选B．
　
13．（2016?苏州）如图，在四边形ABCD中，∠ABC=90°，AB=BC=2，E、F分别是AD、CD的中点，连接BE、BF、EF．若四边形ABCD的面积为6，则△BEF的面积为（　　）21教育网
A．2 B． C． D．3
【解答】解：连接AC，过B作EF的垂线交AC于点G，交EF于点H，
∵∠ABC=90°，AB=BC=2，
∴AC===4，
∵△ABC为等腰三角形，BH⊥AC，
∴△ABG，△BCG为等腰直角三角形，
∴AG=BG=2
∵S△ABC=?AB?AC=×2×2=4，
∴S△ADC=2，
∵=2，
∴GH=BG=，
∴BH=，
又∵EF=AC=2，
∴S△BEF=?EF?BH=×2×=，
故选C．
　
14．（2016?盐城）若a、b、c为△ABC的三边长，且满足|a﹣4|+=0，则c的值可以为（　　）21·cn·jy·com
A．5 B．6 C．7 D．8
【解答】解：∵|a﹣4|+=0，
∴a﹣4=0，a=4；b﹣2=0，b=2；
则4﹣2＜c＜4+2，
2＜c＜6，5符合条件；
故选A．
　
15．（2015?东西湖区校级模拟）如图，∠EOF内有一定点P，过点P的一条直线分别交射线OE于A，射线OF于B．当满足下列哪个条件时，△AOB的面积一定最小（　　）
A．OA=OB B．OP为△AOB的角平分线
C．OP为△AOB的高 D．OP为△AOB的中线
【解答】解：当点P是AB的中点时S△AOB最小；
如图，过点P的另一条直线CD交OE、OF于点C、D，设PD＜PC，过点A作AG∥OF交CD于G，
在△APG和△BPD中，
，
∴△APG≌△BPD（ASA），
S四边形AODG=S△AOB．
∵S四边形AODG＜S△COD，
∴S△AOB＜S△COD，
∴当点P是AB的中点时S△AOB最小；
故选：D．
　
二．填空题（共1小题）
16．（2006?烟台）如图，三角形纸片ABC中，∠A=65°，∠B=75°，将纸片的一角折叠，使点C落在△ABC内，若∠1=20°，则∠2的度数为　60　度．2·1·c·n·j·y
【解答】解：∵∠A=65°，∠B=75°，
∴∠C=180°﹣（65°+75°）=40度，
∴∠CDE+∠CED=180°﹣∠C=140°，
∴∠2=360°﹣（∠A+∠B+∠1+∠CED+∠CDE）=360°﹣300°=60度．
故填60．
　
三．解答题（共14小题）
17．（2015春?邢台校级期末）如图，已知AB∥CD，∠B=120°，∠C=25°，求∠E．
【解答】解：过点E作EF∥AB，如图所示．
∵EF∥AB，
∴∠B+∠BEF=180°，
又∵∠B=120°，
∴∠BEF=60°．
∵EF∥AB∥CD，
∴∠CEF=∠C=25°，
∴∠E=∠BEF+∠CEF=85°．
　
18．（2014春?南京期末）看图填空：
已知：如图，AD⊥BC于D，EF⊥BC于F，交AB于G，交CA延长线于E，∠1=∠2．求证：AD平分∠BAC．
证明：∵AD⊥BC，EF⊥BC（已知）
∴∠ADC=90°，∠EFC=90°（垂线的定义）
∴　∠ADC　=　∠EFC　
　AD　∥　EF　
∴∠1=　∠BAD　
∠2=　∠CAD　
∵∠1=∠2（已知）
∴　∠BAD=∠CAD　
∴AD平分∠BAC（角平分线定义）
【解答】证明：∵AD⊥BC，EF⊥BC，
∴∠ADC=∠EFC=90°，
∴AD∥EF（同位角相等，两直线平行），
∴∠1=∠BAD（两直线平行，内错角相等），
∠2=∠DAC（两直线平行，同位角相等），
∵∠1=∠2（已知），
∴∠BAD=∠DAC（等量代换），
∴AD平分∠BAC，
故答案为：∠ADC，∠EFC，AD，EF，∠BAD，∠CAD，∠BAD=∠CAD．
　
19．（2014秋?剑川县期末）如图，在△ABC中，AE是中线，AD是角平分线，AF是高，BE=2，AF=3，填空：
（1）BE=　CE　=　BC　．
（2）∠BAD=　∠DAC　=　∠BAC　．
（3）∠AFB=　∠AFC　=　90°　．
（4）S△AEC=　3　．
【解答】解：（1）∵AE是中线，
∴BE=CE=BC．
故答案为：CE，BC；
（2）∵AD是角平分线，
∴∠BAD=∠DAC=∠BAC．
故答案为：∠DAC，∠BAC；
（3）∵AF是高，
∴∠AFB=∠AFC=90°．
故答案为：∠AFC，90°；
（4）∵AE是中线，AF是高，BE=2，AF=3，
∴BE=CE=2，
∴S△AEC=CE?AF=×2×3=3．
故答案为：3．
　
20．如图所示．平面上六个点A，B，C，D，E，F构成一个封闭折线图形．求：∠A+∠B+∠C+∠D+∠E+∠F．21世纪教育网版权所有
【解答】解：分析所求的六个角分布在三个三角形中，但需减去顶点位于P，Q，R处的三个内角，由图形结构不难看出，这三个内角可以集中到△PQR中．
在△PAB，△RCD，△QEF中，
∠A+∠B+∠APB=180°，①
∠C+∠D+∠CRD=180°，②
∠E+∠F+∠EQF=180°，③
又在△PQR中∠QPR+∠PRQ+∠PQR=180°，④
又∠APB=∠QPR，∠CRD=∠PRQ，
∠EQF=∠PQR（对顶角相等），
①+②+③﹣④得，
∠A+∠B+∠C+∠D+∠E+∠F=360°．
　
21．如图所示．平面上六个点A，B，C，D，F构成一个封闭折线图形．求∠A+∠B+∠C+∠D+∠E+∠F．
【解答】解：∵∠1=∠A+∠E，∠2=∠B+∠C，
∴∠A+∠B+∠C+∠D+∠E+∠F
=∠1+∠2+∠D=180°．
　
22．如图所示，AB，CD相交于点E，CF，BF分别为∠ACD和∠ABD的平分线且相交于点F，求证：∠F=（∠A+∠D）．
【解答】解：如图所示：
∵CF、BF分别是∠ACD和∠ABD的平分线，
∴∠1=∠2，∠3=∠4，
在△AMC和△FMB中，∠A+∠1=∠3+∠F①，
在△AEC和△DEB中，∠A+∠1+∠2=∠3+∠4+∠D，
即∠A+2∠1=2∠3+∠D②，
由①×2﹣②得，∠A=2∠F﹣∠D，
即2∠F=∠A+∠D，
∴∠F=（∠A+∠D）．
　
23．（2016春?高密市期末）如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠CAB=50°，∠C=60°，求∠DAE和∠BOA的度数．
【解答】解：∵∠A=50°，∠C=60°
∴∠ABC=180°﹣50°﹣60°=70°，
又∵AD是高，
∴∠ADC=90°，
∴∠DAC=180°﹣90°﹣∠C=30°，
∵AE、BF是角平分线，
∴∠CBF=∠ABF=35°，∠EAF=25°，
∴∠DAE=∠DAC﹣∠EAF=5°，
∠AFB=∠C+∠CBF=60°+35°=95°，
∴∠BOA=∠EAF+∠AFB=25°+95°=120°，
∴∠DAC=30°，∠BOA=120°．
故∠DAE=5°，∠BOA=120°．
　
24．（2016春?故城县期末）如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=30°．求：21cnjy.com
（1）∠BAE的度数；
（2）∠DAE的度数；
（3）探究：小明认为如果条件∠B=70°，∠C=30°改成∠B﹣∠C=40°，也能得出∠DAE的度数？若能，请你写出求解过程；若不能，请说明理由．
【解答】解：（1）∵∠B+∠C+∠BAC=180°，
∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣30°=80°，
∵AE平分∠BAC，
∴∠BAE=∠BAC=40°；
（2）∵AD⊥BC，
∴∠ADE=90°，
而∠ADE=∠B+∠BAD，
∴∠BAD=90°﹣∠B=90°﹣70°=20°，
∴∠DAE=∠BAE﹣∠BAD=40°﹣20°=20°；
（3）能．
∵∠B+∠C+∠BAC=180°，
∴∠BAC=180°﹣∠B﹣∠C，
∵AE平分∠BAC，
∴∠BAE=∠BAC=（180°﹣∠B﹣∠C）=90°﹣（∠B+∠C），
∵AD⊥BC，
∴∠ADE=90°，
而∠ADE=∠B+∠BAD，
∴∠BAD=90°﹣∠B，
∴∠DAE=∠BAE﹣∠BAD=90°﹣（∠B+∠C）﹣（90°﹣∠B）=（∠B﹣∠C），
∵∠B﹣∠C=40°，
∴∠DAE=×40°=20°．
　
25．（2016春?淮安期中）在△ABC中，CD⊥AB于D，CE是∠ACB的平分线，∠A=20°，∠B=60°．求∠BCD和∠ECD的度数．www.21-cn-jy.com
【解答】解：∵CD⊥AB，
∴∠CDB=90°，
∵∠B=60°，
∴∠BCD=90°﹣∠B=90°﹣60°=30°；
∵∠A=20°，∠B=60°，∠A+∠B+∠ACB=180°，
∴∠ACB=100°，
∵CE是∠ACB的平分线，
∴∠ACE=∠ACB=50°，
∴∠CEB=∠A+∠ACE=20°+50°=70°，
∠ECD=90°﹣70°=20°
　
26．（2016春?江苏月考）我们知道，任何一个三角形的三条内角平分线相交于一点，如图，若△ABC 的三条内角平分线相交于点I，过I作DE⊥AI分别交AB、AC于点D、E．
（1）请你通过画图、度量，填写右上表（图画在草稿纸上，并尽量画准确）
（2）从上表中你发现了∠BIC与∠BDI之间有何数量关系，请写出来，并说明其中的道理．
∠BAC的度数
40°
60°
90°
120°
∠BIC的度数
∠BDI的度数
【解答】解：（1）填写表格如下：
∠BAC的度数
40°
60°
90°
120°
∠BIC的度数
110°
120°
135°
150°
∠BDI的度数
110°
120°
135°
150°
（2）∠BIC=∠BDI，理由如下：
∵△ABC的三条内角平分线相交于点I，
∴∠BIC=180°﹣（∠IBC+∠ICB）
=180°﹣（∠ABC+∠ACB）
=180°﹣（180°﹣∠BAC）
=90+∠BAC；
∵AI平分∠BAC，
∴∠DAI=∠DAE．
∵DE⊥AI于I，
∴∠AID=90°．
∴∠BDI=∠AID+∠DAI=90°+∠BAC．
∴∠BIC=∠BDI．
　
27．（2015秋?全椒县期中）已知△ABC中，∠ACB=90°，CD为AB边上的高，BE平分∠ABC，分别交CD、AC于点F、E，求证：∠CFE=∠CEF．21·世纪*教育网
【解答】证明：
∵∠ACB=90°，
∴∠1+∠3=90°，
∵CD⊥AB，
∴∠2+∠4=90°，
又∵BE平分∠ABC，
∴∠1=∠2，
∴∠3=∠4，
∵∠4=∠5，
∴∠3=∠5，
即∠CFE=∠CEF．
　
28．（2015秋?泰兴市校级期中）（1）如图（1），已知，在△ABC中，AD，AE分别是△ABC的高和角平分线，若∠B=30°，∠C=50°．求∠DAE的度数；　　21*cnjy*com
（2）如图（2），已知AF平分∠BAC，交边BC于点E，过F作FD⊥BC，若∠B=x°，∠C=（x+36）°，【来源：21cnj*y.co*m】
①∠CAE=　72°﹣x°　（含x的代数式表示）
②求∠F的度数．
【解答】解：（1）∵∠B=30°，∠C=50°，
∴∠CAB=180°﹣∠B﹣∠C=100°，
∵AD是△ABC角平分线，
∴∠CAE=∠CAB=50°，
∵AE分别是△ABC的高，
∴∠ADC=90°，
∴∠CAD=90°﹣∠C=40°，
∴∠DAE=∠CAE﹣∠CAD=50°﹣40°=10°；
（2）①∵∠B=x°，∠C=（x+36）°，AF平分∠BAC，
∴∠EAC=∠BAF，
∴∠CAE=[180°﹣x°﹣（x+36）°]=72°﹣x°，
②∠AEC=∠BAE+∠B=72°，
∵FD⊥BC，
∴∠F=18°．
　
29．（2013春?唐山期末）△ABC中，AD⊥BC，AE平分∠BAC交BC于点E．
（1）∠B=30°，∠C=70°，求∠EAD的大小．
（2）若∠B＜∠C，则2∠EAD与∠C﹣∠B是否相等？若相等，请说明理由．
【解答】解：（1）∵∠B=30°，∠C=70°
∴∠BAC=180°﹣∠B﹣∠C=80°
∵AE是角平分线，
∴∠EAC=∠BAC=40°
∵AD是高，∠C=70°
∴∠DAC=90°﹣∠C=20°
∴∠EAD=∠EAC﹣∠DAC=40°﹣20°=20°；
（2）由（1）知，∠EAD=∠EAC﹣∠DAC=∠BAC﹣（90°﹣∠C）①
把∠BAC=180°﹣∠B﹣∠C代入①，整理得
∠EAD=∠C﹣∠B，
∴2∠EAD=∠C﹣∠B．