4.1 比例线段 同步测试(含解析)
图片预览



文档简介
4.1
比例线段
同步测试
一、单选题
1、已知线段AB,点P是它的黄金分割点,AP>BP,设以AP为边的正方形的面积为S1
,
以PB,AB为边的矩形面积为S2
,
则S1与S2的关系是( )
A、S1>S2
B、S1<S2
C、S1=S2
D、S1≥S2
【答案】
C
【考点】
黄金分割
【解析】
【解答】解:
根据黄金分割的概念得:
,
即S1=S2
.
故选C.
【分析】根据黄金分割的概念表示出比例式,再结合正方形的面积进行分析计算.
2、已知点C是AB的黄金分割点(AC>BC),若AB=4cm,则AC的长为( )
A、(2﹣2)cm
B、(6﹣2)cm
C、(﹣1)cm
D、(3﹣)cm
【答案】
A
【考点】
黄金分割
【解析】
【解答】解:由题意知:AC=AB=4×=2(
﹣1)=2﹣2.
故选A.
【分析】把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值(
)叫做黄金比,AC=4×=2(
﹣1).
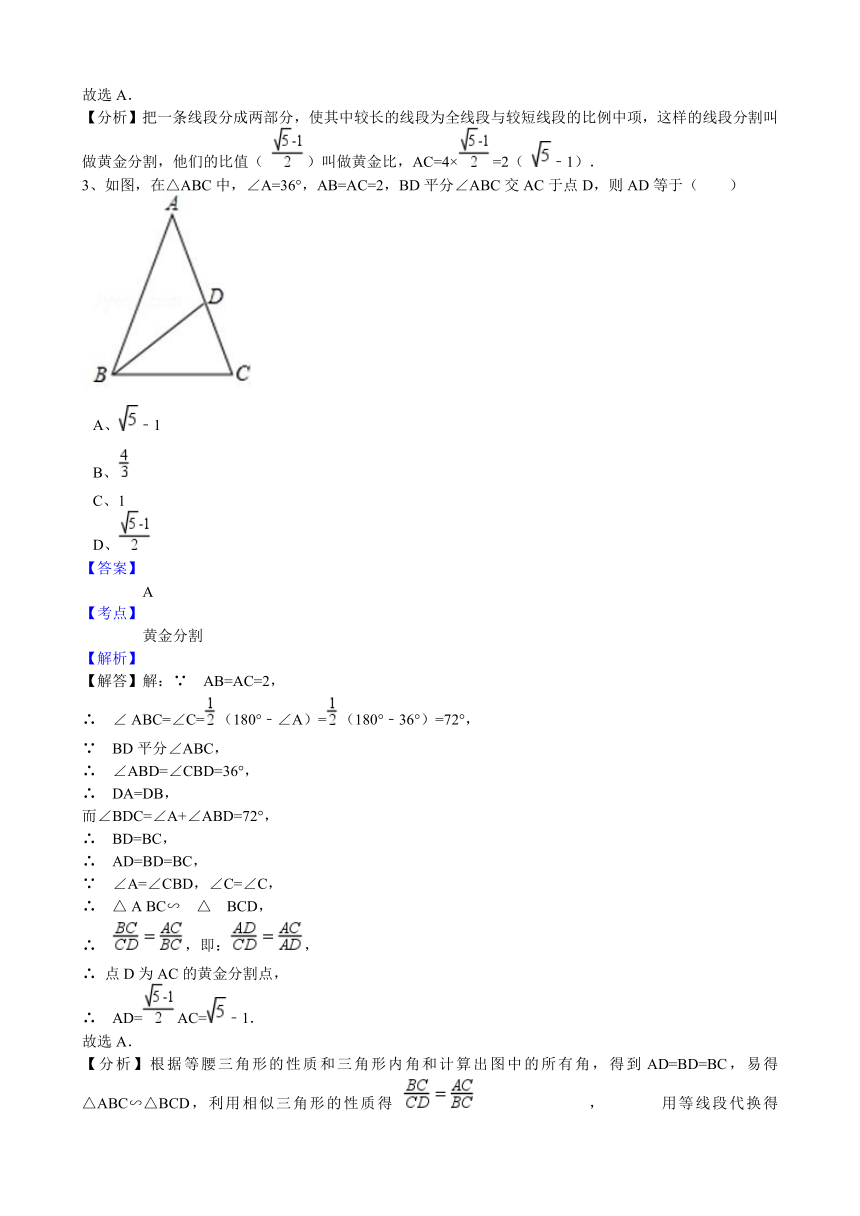
3、如图,在△ABC中,∠A=36°,AB=AC=2,BD平分∠ABC交AC于点D,则AD等于( )
A、﹣1
B、
C、1
D、
【答案】
A
【考点】
黄金分割
【解析】
【解答】解:∵
AB=AC=2,
∴
∠
ABC=∠C=(180°﹣∠A)=(180°﹣36°)=72°,
∵
BD平分∠ABC,
∴
∠ABD=∠CBD=36°,
∴
DA=DB,
而∠BDC=∠A+∠ABD=72°,
∴
BD=BC,
∴
AD=BD=BC,
∵
∠A=∠CBD,∠C=∠C,
∴
△
A
BC∽
△
BCD,
∴
,即:,
∴
点D为AC的黄金分割点,
∴
AD=AC=﹣1.
故选A.
【分析】根据等腰三角形的性质和三角形内角和计算出图中的所有角,得到AD=BD=BC,易得△ABC∽△BCD,利用相似三角形的性质得
,
用等线段代换得
,则根据黄金分割的定义可判断点D为AC的黄金分割点,所以AD=AC=﹣1.
4、某校要举办国庆联欢会,主持人站在舞台的黄金分割点处最自然得体.如图,若舞台AB的长为20m,C为AB的一个黄金分割点(AC<BC),则AC的长为(结果精确到0.1m)( )
A、6.7m
B、7.6m
C、10m
D、12.4m
【答案】
B
【考点】
黄金分割
【解析】
【解答】解:∵
C为AB的一个黄金分割点,
∴
BC=AB≈12.4cm,
∴
AC=20﹣12.4=7.6(cm),
故选:B.
【分析】根据黄金比值约为0.618进行计算即可.
5、爱美之心人皆有之,特别是很多女士,穿上高跟鞋后往往会有很好的效果,事实上,当人体的下半身长度与身高的比值接近0.618时,会给人以美感,某女士身高165cm,下半身长与身高的比值是0.60,为了尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )
A、4cm
B、6cm
C、8cm
D、10cm
【答案】
C
【考点】
黄金分割
【解析】
【解答】解:根据已知条件得下半身长是160×0.6=96cm,
设需要穿的高跟鞋是ycm,
则根据黄金分割的定义得:
=0.618,
解得:y≈8cm.
故选C.
【分析】先求出下半身的长度,然后再根据黄金分割的定义求解.
6、把10cm长的线段进行黄金分割,则较长线段的长(≈2.236,精确到0.01)是( )
A、3.09cm
B、3.82cm
C、6.18cm
D、7.00cm
【答案】
C
【考点】
黄金分割
【解析】
【解答】解:根据题意得:
较长线段的长是10×=10×0.618=6.18cm.
故选C.
【分析】把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值()叫做黄金比.
7、根据有关测定,当外界气温处于人体正常体温的黄金比值时,人体感到最舒适(人体正常体温约为37℃),这个气温大约为( )
A、23℃
B、28℃
C、30℃
D、37℃
【答案】
A
【考点】
黄金分割
【解析】
【解答】解:根据黄金比的值得:37×0.618≈23℃.
故选A.
【分析】根据黄金比的值知,身体感到特别舒适的温度应为37度的0.618倍.
8、若a:b=3:2,b:c=4:3,则
的值是( )
A、2
B、-2
C、3
D、-3
【答案】
B
【考点】
比例的性质
【解析】
【解答】解:由a:b=3:2,b:c=4:3,得
a=b,c=b.
故选:B.
【分析】根据比例的性质,可用b表示a,c,根据分式的性质,可得答案.
9、若3x=4y(xy≠0),则下列比例式成立的是( )
A、=
B、
C、
D、
【答案】
A
【考点】
比例的性质
【解析】
【解答】解:A、由比例的性质,得3x=4y,故A正确;
B、由比例的性质,得xy=12,故B错误;
C、由比例的性质,得4x=3y,故C错误;
D、由比例的性质,得4x=3y,故D错误;
故选:A.
【分析】根据比例的性质,可得答案.
10、若非零实数x,y满足4y=3x,则x:y等于( )
A、3:4
B、4:3
C、2:3
D、3:2
【答案】
B
【考点】
比例的性质
【解析】
【解答】解:∵4y=3x,
∴x:y=4:3,
故选:B.
【分析】根据比例的性质,即可解答.
11、如图,扇子的圆心角为x°,余下扇形的圆心角为y°,x与y的比通常按黄金比来设计,这样的扇子外形比较美观,若黄金比取0.6,则x为( )
A、144°
B、135°
C、136°
D、108°
【答案】
B
【考点】
黄金分割
【解析】
【解答】解:由扇子的圆心角为x°,余下扇形的圆心角为y°,黄金比为0.6,
根据题意得:x:y=0.6=3:5,
又∵
x+y=360,
则x=360×=135.
故选B.
【分析】由题意得到x与y的比值应为黄金比,根据黄金比为0.6,得到x与y比值为0.6,即为3:5,又根据扇子的圆心角与余下的圆心角刚好构成周角,即x与y之和为360,根据比例性质即可求出x的值.
12、如图,若DC∥FE∥AB,则有( )
A、
B、
C、
D、
【答案】
D
【考点】
平行线分线段成比例
【解析】
【解答】解:∵
DC∥FE∥AB,
∴
OD:OE=OC:OF(A错误);
OF:OA=OE:OB≠OB:OC(B错误);
OA:OC=OB:OD(C错误);
CD:EF=OD:OE(D正确).
故选D.
【分析】根据平行线分线段成比例定理,根据题意直接列出比例等式,对比选项即可得出答案.
13、如图,在△
ABC中,DE∥
BC,分别交AB,AC于点D,E.若AD=2,DB=4,则
的值为( )
A、
B、
C、
D、
【答案】
B
【考点】
平行线分线段成比例
【解析】
【解答】解:∵
DE∥
BC,
∴
.
故选:B.
【分析】首先根据平行线分线段成比例定理得出比例式,即可得出结果.
14、如图,在△ABC中,D、E分别是AB、AC的点,且DE∥BC,如果AD=2cm,DB=1cm,DE=1.6cm,则BC=( )
A、0.8cm
B、2cm
C、2.4cm
D、3.2cm
【答案】
C
【考点】
平行线分线段成比例
【解析】
【解答】解:∵
AD=2cm,DB=1cm,
∴
AB=AD+DB=3cm,
∵
DE∥
BC,
∴
,
解得:BC=2.4.
故选:C.
【分析】由平行线分线段成比例可得
,
把线段代入可求得BC.
15、如图,直线l1、l2、…l6是一组等距离的平行线,过直线l1上的点A作两条射线,分别与直线l3
,
l6相交于点B、E、C、F.若BC=2,则EF的长是( )
A、4
B、5
C、6
D、7
【答案】
B
【考点】
平行线分线段成比例
【解析】
【解答】解:∵
l3∥
l6
,
∴
BC∥
EF,
∴
△
ABC∽
△
AEF,
∴
,
∵
BC=2,
∴
EF=5.
故选B.
【分析】由直线l1、l2、…l6是一组等距的平行线,得到△ABC∽△AEF,推出比例式求得结果.
二、填空题
16、已知C、D是线段AB的两个黄金分割点,AB=2,则CD的长是________.(用含根号的式子表示)
【答案】
①2﹣4
【考点】
黄金分割
【解析】
【解答】解:如图,C、D是线段AB的两个黄金分割点,设AC>BC,AD<BD,
根据题意得AC=AB=×2=﹣1,
BD=AB=×2=﹣1,
则AD=AB﹣BD=2﹣(﹣1)=3﹣,
所以CD=AC﹣AD=﹣1﹣(3﹣)=2﹣4.
故答案为2﹣4.
【分析】AC>BC,AD<BD,根据黄金分割的定义先计算出AC=BD=﹣1,再计算出AD,然后利用CD=AC﹣AD进行计算.
17、线段AB长10cm,点P在线段AB上,且满足
,
那么AP的长为________ cm.
【答案】
①5﹣5
【考点】
黄金分割
【解析】
【解答】解:设AP=x,则BP=10﹣x,
∵
,
∴
,
∴
x1=5﹣5,x2=﹣5﹣5(不合题意,舍去),
∴
AP的长为(5﹣5)cm.
故答案为:5﹣5.
【分析】设AP=x,根据线段AB长10cm,得出BP=10﹣x,再根据,
求出x的值即可得出答案.
18、若=2,则
的值为________
【答案】
①2
【考点】
比例的性质
【解析】
【解答】解:由=2,得a=2b.
,
故答案为:2.
【分析】根据等式的性质,可用b表示a,根据分式的性质,可得答案.
19、若x:y=5:2,则(x+y):y的值是________
【答案】
①
【考点】
比例的性质
【解析】
【解答】解:由合比性质,得
,
故答案为:.
【分析】根据合比性质:
,
可得答案.
20、如图,△ABC中,AB=7,BC=6,AC=8,延长∠ABC、∠ACB的角平分线BD、CE分别交过点A且平行于BC的直线于N、M,BD与CE相交于点G,则△BCG与△MNG的面积之比是________ .
【答案】
①4:25
【考点】
平行线分线段成比例
【解析】
【解答】解:∵
CE是∠ACB的角平分线,
∴
,
∵
MN∥BC,
∴
,
同理,
,
∴
,
∵
MN∥
BC,
∴
△
BCG∽
△
MNG,
∴
△
BCG与△
MNG的面积之比是4:25.
故答案为:4:25.
【分析】根据角平分线的性质求出,根据相似三角形的面积比等于相似比的平方解答.,
三、计算题
21、若
,求
的值.
【答案】
解答:设
,
则
,
,
,
所以
.
【考点】
比例的性质
【解析】
分析:先设
,可得
,
,
,再把a、b、c的值都代入所求式子计算即可.
22、已知
,求
.
【答案】
解答:令
,
∴
,
,
,
∴
原式
.
【考点】
比例的性质
【解析】
分析:设
,
,
,再代入原式即可得出答案.
四、解答题
23、如图,△
ABC中,AB=AC,∠
A=36°,BD平分∠
ABC.求证:
=.
【答案】
解∵AB=AC,∠
A=36°,
∴
∠
ABC=∠
C=(180°﹣36°)=72°,
∵BD平分∠
ABC,
∴
∠
ABD=∠
CBD=∠ABC=36°,
∴
DA=DB,
∵
∠
B
DC=∠
A+∠
ABD=72°,
∴
BD=BC,
∴
AD=BC,
∵
∠
A=∠
CBD,∠
C=∠
C,
∴
△
ABC∽
△
BDC,
∴
BC:DC=AC:BC,
∴
AD:DC=AC:AD,
∴
点D为AC的黄金分割点,
∴=,
∴=.
【考点】
黄金分割
【解析】
【分析】根据等腰三角形的性质和角平分线的定义证明△ABC∽△BDC,根据黄金分割的概念计算即可.
24、定义:如图1,点C在线段AB上,若满足AC2=BC AB,则称点C为线段AB的黄金分割点.如图2,△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D.
(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
【答案】
(1)证明:∵
AB=AC=1,
∴
∠
ABC=∠
C=(180°﹣∠
A)=(180°﹣36°)=72°,
∵
BD平分∠ABC交AC于点D,
∴
∠
ABD=∠CBD=∠ABC=36°,
∴
∠
BDC=180°﹣36°﹣72°=72°,
∴
DA=DB,BD=BC,
∴
AD=BD=BC,
易得△
BDC∽
△
ABC,
∴
BC:AC=CD:BC,即BC2=CD AC,
∴
AD2=CD AC,
∴
点D是线段AC的黄金分割点;
(2)设AD=x,则CD=AC﹣AD=1﹣x,
∵
AD2=CD AC,
∴
x2=1﹣x,解得x1=,x2=,
即AD的长为.
【考点】
黄金分割
【解析】
【分析】(1)利用等腰三角形的性质和三角形内角和定理可计算出∠ABC=∠C=72°,∠ABD=∠CBD=36°,∠BDC=72°,则可得
到AD=BD=BC,然后根据相似三角形的判定方法易得△BDC∽△ABC,利用相似比得到BC2=CD AC,于是有AD2=CD AC,则可根据线段黄金分割点的定义得到结论;
(2)设AD=x,则CD=AC﹣AD=1﹣x,由(1)的结论得到x2=1﹣x,然后解方程即可得到AD的长.
五、综合题
25、(2016 内江)已知抛物线C:y=x2﹣3x+m,直线l:y=kx(k>0),当k=1时,抛物线C与直线l只有一个公共点.
(1)求m的值;
(2)若直线l与抛物线C交于不同的两点A,B,直线l与直线l1:y=﹣3x+b交于点P,且
+
=
,求b的值;
(3)在(2)的条件下,设直线l1与y轴交于点Q,问:是否在实数k使S△APQ=S△BPQ?若存在,求k的值,若不存在,说明理由.
【答案】
(1)解:当k=1时,抛物线C与直线l只有一个公共点,
∴
直线l解析式为y=x,
∵
,
∴
x2﹣3x+m=x,
∴
x2﹣4x+m=0,
∴
△
=16﹣4m=0,
∴
m=4
(2)解:如图,
分别过点A,P,B作y轴的垂线,垂足依次为C,D,E,
则△
OAC∽
△
OPD,∴
.
同理,
.
∵
,
∴
=2.
∴
=2.
∴
,
即
.
解方程组
,
得x=x=
,
即PD=
.
由方程组
消去y,得x2﹣(k+3)x+4=0.
∵
AC,BE是以上一元二次方程的两根,
∴
AC+BE=k+3,AC×BE=4.
∴
.
解得b=8.
(3)解:不存在.理由如下:
假设存在,
当S△APQ=S△BPQ时,有AP=PB,
于是PD﹣AC=PE﹣PD,
即AC+BE=2PD.
由(2)可知AC+BE=k+3,PD=
,
∴
k+3=2×
,
即(k+3)2=16.
解得k=1(舍去k=﹣7).
当k=1时,A,B两点重合,△BQA不存在.
∴
不存在实数k使S△APQ=S△BPQ
【考点】
根与系数的关系,比例的性质,相似三角形的判定与性质
【解析】
【分析】(1)两图象有一个交点,则对应的方程组有一组解,即△=0,代入计算即可求出m的值;(2)作出辅助线,得到△OAC∽△OPD,
+
=2,同理
+
=2,AC,BE是x2﹣(k+3)x+4=0两根,即可;(3)由S△APQ=S△BPQ得到AC+BE=2PD,建立方程(k+3)2=16即可.此题是二次函数综合题,主要考查了相似三角形的性质和判定,比例的性质,一元二次方程的根与系数的关系,解本题的关键是灵活运用根与系数的关系.
比例线段
同步测试
一、单选题
1、已知线段AB,点P是它的黄金分割点,AP>BP,设以AP为边的正方形的面积为S1
,
以PB,AB为边的矩形面积为S2
,
则S1与S2的关系是( )
A、S1>S2
B、S1<S2
C、S1=S2
D、S1≥S2
【答案】
C
【考点】
黄金分割
【解析】
【解答】解:
根据黄金分割的概念得:
,
即S1=S2
.
故选C.
【分析】根据黄金分割的概念表示出比例式,再结合正方形的面积进行分析计算.
2、已知点C是AB的黄金分割点(AC>BC),若AB=4cm,则AC的长为( )
A、(2﹣2)cm
B、(6﹣2)cm
C、(﹣1)cm
D、(3﹣)cm
【答案】
A
【考点】
黄金分割
【解析】
【解答】解:由题意知:AC=AB=4×=2(
﹣1)=2﹣2.
故选A.
【分析】把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值(
)叫做黄金比,AC=4×=2(
﹣1).
3、如图,在△ABC中,∠A=36°,AB=AC=2,BD平分∠ABC交AC于点D,则AD等于( )
A、﹣1
B、
C、1
D、
【答案】
A
【考点】
黄金分割
【解析】
【解答】解:∵
AB=AC=2,
∴
∠
ABC=∠C=(180°﹣∠A)=(180°﹣36°)=72°,
∵
BD平分∠ABC,
∴
∠ABD=∠CBD=36°,
∴
DA=DB,
而∠BDC=∠A+∠ABD=72°,
∴
BD=BC,
∴
AD=BD=BC,
∵
∠A=∠CBD,∠C=∠C,
∴
△
A
BC∽
△
BCD,
∴
,即:,
∴
点D为AC的黄金分割点,
∴
AD=AC=﹣1.
故选A.
【分析】根据等腰三角形的性质和三角形内角和计算出图中的所有角,得到AD=BD=BC,易得△ABC∽△BCD,利用相似三角形的性质得
,
用等线段代换得
,则根据黄金分割的定义可判断点D为AC的黄金分割点,所以AD=AC=﹣1.
4、某校要举办国庆联欢会,主持人站在舞台的黄金分割点处最自然得体.如图,若舞台AB的长为20m,C为AB的一个黄金分割点(AC<BC),则AC的长为(结果精确到0.1m)( )
A、6.7m
B、7.6m
C、10m
D、12.4m
【答案】
B
【考点】
黄金分割
【解析】
【解答】解:∵
C为AB的一个黄金分割点,
∴
BC=AB≈12.4cm,
∴
AC=20﹣12.4=7.6(cm),
故选:B.
【分析】根据黄金比值约为0.618进行计算即可.
5、爱美之心人皆有之,特别是很多女士,穿上高跟鞋后往往会有很好的效果,事实上,当人体的下半身长度与身高的比值接近0.618时,会给人以美感,某女士身高165cm,下半身长与身高的比值是0.60,为了尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )
A、4cm
B、6cm
C、8cm
D、10cm
【答案】
C
【考点】
黄金分割
【解析】
【解答】解:根据已知条件得下半身长是160×0.6=96cm,
设需要穿的高跟鞋是ycm,
则根据黄金分割的定义得:
=0.618,
解得:y≈8cm.
故选C.
【分析】先求出下半身的长度,然后再根据黄金分割的定义求解.
6、把10cm长的线段进行黄金分割,则较长线段的长(≈2.236,精确到0.01)是( )
A、3.09cm
B、3.82cm
C、6.18cm
D、7.00cm
【答案】
C
【考点】
黄金分割
【解析】
【解答】解:根据题意得:
较长线段的长是10×=10×0.618=6.18cm.
故选C.
【分析】把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值()叫做黄金比.
7、根据有关测定,当外界气温处于人体正常体温的黄金比值时,人体感到最舒适(人体正常体温约为37℃),这个气温大约为( )
A、23℃
B、28℃
C、30℃
D、37℃
【答案】
A
【考点】
黄金分割
【解析】
【解答】解:根据黄金比的值得:37×0.618≈23℃.
故选A.
【分析】根据黄金比的值知,身体感到特别舒适的温度应为37度的0.618倍.
8、若a:b=3:2,b:c=4:3,则
的值是( )
A、2
B、-2
C、3
D、-3
【答案】
B
【考点】
比例的性质
【解析】
【解答】解:由a:b=3:2,b:c=4:3,得
a=b,c=b.
故选:B.
【分析】根据比例的性质,可用b表示a,c,根据分式的性质,可得答案.
9、若3x=4y(xy≠0),则下列比例式成立的是( )
A、=
B、
C、
D、
【答案】
A
【考点】
比例的性质
【解析】
【解答】解:A、由比例的性质,得3x=4y,故A正确;
B、由比例的性质,得xy=12,故B错误;
C、由比例的性质,得4x=3y,故C错误;
D、由比例的性质,得4x=3y,故D错误;
故选:A.
【分析】根据比例的性质,可得答案.
10、若非零实数x,y满足4y=3x,则x:y等于( )
A、3:4
B、4:3
C、2:3
D、3:2
【答案】
B
【考点】
比例的性质
【解析】
【解答】解:∵4y=3x,
∴x:y=4:3,
故选:B.
【分析】根据比例的性质,即可解答.
11、如图,扇子的圆心角为x°,余下扇形的圆心角为y°,x与y的比通常按黄金比来设计,这样的扇子外形比较美观,若黄金比取0.6,则x为( )
A、144°
B、135°
C、136°
D、108°
【答案】
B
【考点】
黄金分割
【解析】
【解答】解:由扇子的圆心角为x°,余下扇形的圆心角为y°,黄金比为0.6,
根据题意得:x:y=0.6=3:5,
又∵
x+y=360,
则x=360×=135.
故选B.
【分析】由题意得到x与y的比值应为黄金比,根据黄金比为0.6,得到x与y比值为0.6,即为3:5,又根据扇子的圆心角与余下的圆心角刚好构成周角,即x与y之和为360,根据比例性质即可求出x的值.
12、如图,若DC∥FE∥AB,则有( )
A、
B、
C、
D、
【答案】
D
【考点】
平行线分线段成比例
【解析】
【解答】解:∵
DC∥FE∥AB,
∴
OD:OE=OC:OF(A错误);
OF:OA=OE:OB≠OB:OC(B错误);
OA:OC=OB:OD(C错误);
CD:EF=OD:OE(D正确).
故选D.
【分析】根据平行线分线段成比例定理,根据题意直接列出比例等式,对比选项即可得出答案.
13、如图,在△
ABC中,DE∥
BC,分别交AB,AC于点D,E.若AD=2,DB=4,则
的值为( )
A、
B、
C、
D、
【答案】
B
【考点】
平行线分线段成比例
【解析】
【解答】解:∵
DE∥
BC,
∴
.
故选:B.
【分析】首先根据平行线分线段成比例定理得出比例式,即可得出结果.
14、如图,在△ABC中,D、E分别是AB、AC的点,且DE∥BC,如果AD=2cm,DB=1cm,DE=1.6cm,则BC=( )
A、0.8cm
B、2cm
C、2.4cm
D、3.2cm
【答案】
C
【考点】
平行线分线段成比例
【解析】
【解答】解:∵
AD=2cm,DB=1cm,
∴
AB=AD+DB=3cm,
∵
DE∥
BC,
∴
,
解得:BC=2.4.
故选:C.
【分析】由平行线分线段成比例可得
,
把线段代入可求得BC.
15、如图,直线l1、l2、…l6是一组等距离的平行线,过直线l1上的点A作两条射线,分别与直线l3
,
l6相交于点B、E、C、F.若BC=2,则EF的长是( )
A、4
B、5
C、6
D、7
【答案】
B
【考点】
平行线分线段成比例
【解析】
【解答】解:∵
l3∥
l6
,
∴
BC∥
EF,
∴
△
ABC∽
△
AEF,
∴
,
∵
BC=2,
∴
EF=5.
故选B.
【分析】由直线l1、l2、…l6是一组等距的平行线,得到△ABC∽△AEF,推出比例式求得结果.
二、填空题
16、已知C、D是线段AB的两个黄金分割点,AB=2,则CD的长是________.(用含根号的式子表示)
【答案】
①2﹣4
【考点】
黄金分割
【解析】
【解答】解:如图,C、D是线段AB的两个黄金分割点,设AC>BC,AD<BD,
根据题意得AC=AB=×2=﹣1,
BD=AB=×2=﹣1,
则AD=AB﹣BD=2﹣(﹣1)=3﹣,
所以CD=AC﹣AD=﹣1﹣(3﹣)=2﹣4.
故答案为2﹣4.
【分析】AC>BC,AD<BD,根据黄金分割的定义先计算出AC=BD=﹣1,再计算出AD,然后利用CD=AC﹣AD进行计算.
17、线段AB长10cm,点P在线段AB上,且满足
,
那么AP的长为________ cm.
【答案】
①5﹣5
【考点】
黄金分割
【解析】
【解答】解:设AP=x,则BP=10﹣x,
∵
,
∴
,
∴
x1=5﹣5,x2=﹣5﹣5(不合题意,舍去),
∴
AP的长为(5﹣5)cm.
故答案为:5﹣5.
【分析】设AP=x,根据线段AB长10cm,得出BP=10﹣x,再根据,
求出x的值即可得出答案.
18、若=2,则
的值为________
【答案】
①2
【考点】
比例的性质
【解析】
【解答】解:由=2,得a=2b.
,
故答案为:2.
【分析】根据等式的性质,可用b表示a,根据分式的性质,可得答案.
19、若x:y=5:2,则(x+y):y的值是________
【答案】
①
【考点】
比例的性质
【解析】
【解答】解:由合比性质,得
,
故答案为:.
【分析】根据合比性质:
,
可得答案.
20、如图,△ABC中,AB=7,BC=6,AC=8,延长∠ABC、∠ACB的角平分线BD、CE分别交过点A且平行于BC的直线于N、M,BD与CE相交于点G,则△BCG与△MNG的面积之比是________ .
【答案】
①4:25
【考点】
平行线分线段成比例
【解析】
【解答】解:∵
CE是∠ACB的角平分线,
∴
,
∵
MN∥BC,
∴
,
同理,
,
∴
,
∵
MN∥
BC,
∴
△
BCG∽
△
MNG,
∴
△
BCG与△
MNG的面积之比是4:25.
故答案为:4:25.
【分析】根据角平分线的性质求出,根据相似三角形的面积比等于相似比的平方解答.,
三、计算题
21、若
,求
的值.
【答案】
解答:设
,
则
,
,
,
所以
.
【考点】
比例的性质
【解析】
分析:先设
,可得
,
,
,再把a、b、c的值都代入所求式子计算即可.
22、已知
,求
.
【答案】
解答:令
,
∴
,
,
,
∴
原式
.
【考点】
比例的性质
【解析】
分析:设
,
,
,再代入原式即可得出答案.
四、解答题
23、如图,△
ABC中,AB=AC,∠
A=36°,BD平分∠
ABC.求证:
=.
【答案】
解∵AB=AC,∠
A=36°,
∴
∠
ABC=∠
C=(180°﹣36°)=72°,
∵BD平分∠
ABC,
∴
∠
ABD=∠
CBD=∠ABC=36°,
∴
DA=DB,
∵
∠
B
DC=∠
A+∠
ABD=72°,
∴
BD=BC,
∴
AD=BC,
∵
∠
A=∠
CBD,∠
C=∠
C,
∴
△
ABC∽
△
BDC,
∴
BC:DC=AC:BC,
∴
AD:DC=AC:AD,
∴
点D为AC的黄金分割点,
∴=,
∴=.
【考点】
黄金分割
【解析】
【分析】根据等腰三角形的性质和角平分线的定义证明△ABC∽△BDC,根据黄金分割的概念计算即可.
24、定义:如图1,点C在线段AB上,若满足AC2=BC AB,则称点C为线段AB的黄金分割点.如图2,△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D.
(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
【答案】
(1)证明:∵
AB=AC=1,
∴
∠
ABC=∠
C=(180°﹣∠
A)=(180°﹣36°)=72°,
∵
BD平分∠ABC交AC于点D,
∴
∠
ABD=∠CBD=∠ABC=36°,
∴
∠
BDC=180°﹣36°﹣72°=72°,
∴
DA=DB,BD=BC,
∴
AD=BD=BC,
易得△
BDC∽
△
ABC,
∴
BC:AC=CD:BC,即BC2=CD AC,
∴
AD2=CD AC,
∴
点D是线段AC的黄金分割点;
(2)设AD=x,则CD=AC﹣AD=1﹣x,
∵
AD2=CD AC,
∴
x2=1﹣x,解得x1=,x2=,
即AD的长为.
【考点】
黄金分割
【解析】
【分析】(1)利用等腰三角形的性质和三角形内角和定理可计算出∠ABC=∠C=72°,∠ABD=∠CBD=36°,∠BDC=72°,则可得
到AD=BD=BC,然后根据相似三角形的判定方法易得△BDC∽△ABC,利用相似比得到BC2=CD AC,于是有AD2=CD AC,则可根据线段黄金分割点的定义得到结论;
(2)设AD=x,则CD=AC﹣AD=1﹣x,由(1)的结论得到x2=1﹣x,然后解方程即可得到AD的长.
五、综合题
25、(2016 内江)已知抛物线C:y=x2﹣3x+m,直线l:y=kx(k>0),当k=1时,抛物线C与直线l只有一个公共点.
(1)求m的值;
(2)若直线l与抛物线C交于不同的两点A,B,直线l与直线l1:y=﹣3x+b交于点P,且
+
=
,求b的值;
(3)在(2)的条件下,设直线l1与y轴交于点Q,问:是否在实数k使S△APQ=S△BPQ?若存在,求k的值,若不存在,说明理由.
【答案】
(1)解:当k=1时,抛物线C与直线l只有一个公共点,
∴
直线l解析式为y=x,
∵
,
∴
x2﹣3x+m=x,
∴
x2﹣4x+m=0,
∴
△
=16﹣4m=0,
∴
m=4
(2)解:如图,
分别过点A,P,B作y轴的垂线,垂足依次为C,D,E,
则△
OAC∽
△
OPD,∴
.
同理,
.
∵
,
∴
=2.
∴
=2.
∴
,
即
.
解方程组
,
得x=x=
,
即PD=
.
由方程组
消去y,得x2﹣(k+3)x+4=0.
∵
AC,BE是以上一元二次方程的两根,
∴
AC+BE=k+3,AC×BE=4.
∴
.
解得b=8.
(3)解:不存在.理由如下:
假设存在,
当S△APQ=S△BPQ时,有AP=PB,
于是PD﹣AC=PE﹣PD,
即AC+BE=2PD.
由(2)可知AC+BE=k+3,PD=
,
∴
k+3=2×
,
即(k+3)2=16.
解得k=1(舍去k=﹣7).
当k=1时,A,B两点重合,△BQA不存在.
∴
不存在实数k使S△APQ=S△BPQ
【考点】
根与系数的关系,比例的性质,相似三角形的判定与性质
【解析】
【分析】(1)两图象有一个交点,则对应的方程组有一组解,即△=0,代入计算即可求出m的值;(2)作出辅助线,得到△OAC∽△OPD,
+
=2,同理
+
=2,AC,BE是x2﹣(k+3)x+4=0两根,即可;(3)由S△APQ=S△BPQ得到AC+BE=2PD,建立方程(k+3)2=16即可.此题是二次函数综合题,主要考查了相似三角形的性质和判定,比例的性质,一元二次方程的根与系数的关系,解本题的关键是灵活运用根与系数的关系.
同课章节目录
