浙教版九年级上数学《4.1 比例线段(3)》课件
文档属性
| 名称 | 浙教版九年级上数学《4.1 比例线段(3)》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-08 08:56:28 | ||
图片预览






文档简介
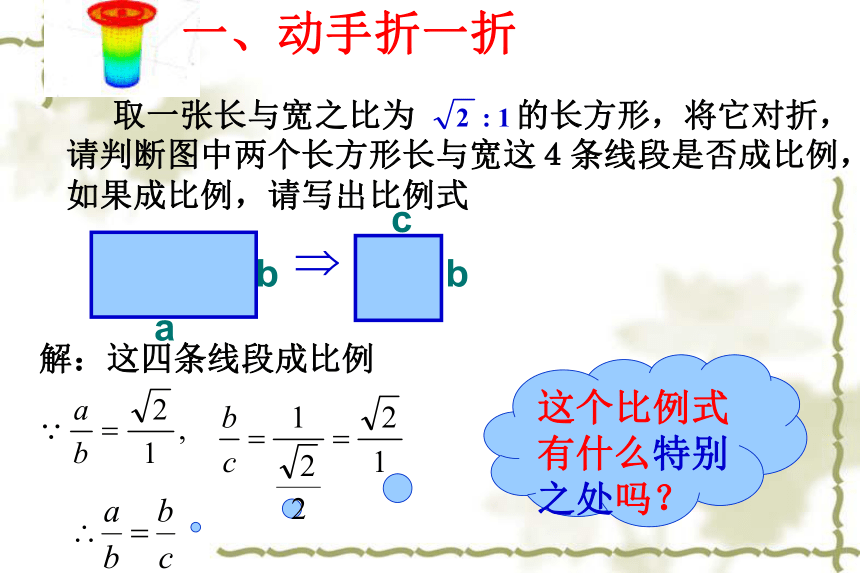
课件21张PPT。§4.1 比例线段(3)浙教版九年级《数学》上册第四章 相似图形数学缔造完美 取一张长与宽之比为 的长方形,将它对折,请判断图中两个长方形长与宽这4条线段是否成比例,如果成比例,请写出比例式abbc这个比例式有什么特别之处吗?一、动手折一折解:这四条线段成比例一般地,如果三个数a,b,c满足比例式
, 则b就
叫a,c的比例中项用符号语言表示为:定义: 例题分析 例1. (1) 1是不是 和的比例中项?如果是比例中项,请写出相应的比例式.
(2) 2和8的比例中项是________温馨提示:线段比例中项与数的比例中项是两个不同的概念,前者是一个正数,而后者是一对互为相反数.
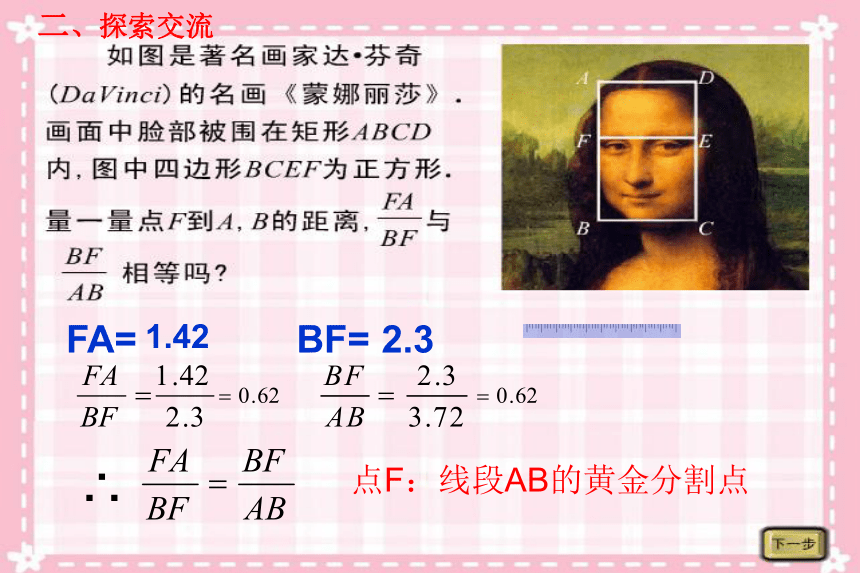
1.求下列线段a、b的比例中项.(1)a=3,b=27; 课内练习:±4FA= BF=∴1.422.3 二、探索交流
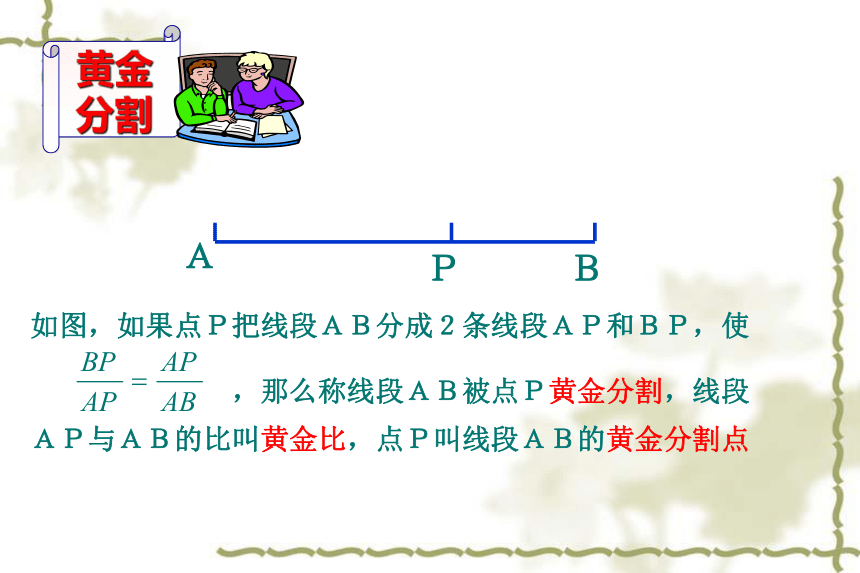
点F:线段AB的黄金分割点利用一元二次方程的知识,可以求出黄金比的数值几,即 的值设AB=a, AP=xxa-x历史上,人们视黄金分割为“最美丽”的几何比率。 她的上半身(以肚脐眼为分界点)和下半身的比值接近0.618. 世界艺术珍品——维纳斯女神, 她是西元前一百多年希腊雕塑鼎盛时期的代表作,请你欣赏 感受匀称 协调之美欣赏之一:芭蕾舞欣赏之二:
468m289.2m上海东方明珠电视塔高468m,上球体到塔底的距离约为289.2m, 289.2与468的比值是一个神奇的数字,这个塔的设计精巧,外型匀称、漂亮、美观、大方.欣赏之三:上海东方明珠塔例3.已知点C是线段AB的黄金分割点,且AC>CB则下列等式成立的是( )
(A) AB2=AC?CB (B) CB2=AC?AB
(C) AC2=CB?AB (D) AC2=AB?BC
例题分析例4.如图,点P是线段AB的黄金分割点,且AP>BP(1)请写出黄金分割的比例式,并指出比例中项(3)若AB=2,求PBD1.经过点B作BD⊥AB,使2.连接AD,在AD上截取DE=DB.3.在AB上截取AC=AE.你能验证这个结论吗?相信你完成下列两个小题后就会有答案.三、动手画一画 找黄金分割点已知线段AB=a,用直尺和圆规作出它的黄金分割点作法:2.请计算1.如果设AB=1,那BD,AD,AC,BC分别等于多少?点C就是所求线段AB的黄金分割点黄金分割的深远意义
历史上,人们视黄金分割为“最美丽”的几何比率,广泛应用于建筑和雕刻中,如古代希腊的帕特农神庙、埃及金字塔、上海东方明珠塔等,一些长方形的画框,宽与长之比也设计成0.618,在自然界中也有很多例子,美丽的蝴蝶身长与双翅展开后的长度之比约为0.618.许多美丽的形状都与0.618这个比值有关。古希腊的一些神庙,在建筑时高和宽也是按
黄金比0.618来建立,他们认为这样的长方形
看来是较美观;其大理石柱廓,就是根据黄金
分割律分割整个神庙的.帕特农神庙五、应用新知 体验成功你能用所学的知识解释帕特农神庙建筑中所蕴含的数学道理吗?
请用所学知识回答上面的问题这时的矩形ABCD称黄金矩形1.作顶角为36°的等腰△ABC;量出
底BC与腰AB的长度,计算: ;
2.作∠B的平分线,交AC于点D,量出CD的长度,
再计算: . (精确到0.001)0.6180.618☆再作∠C的平分线,交BD于E,
△CDE也是黄金三角形……☆顶角为36°的等腰三角形称为 黄金三角形 ☆点D是线段AC的黄金分割点.六、拓展新知 七、生活中的黄金分割1.小明家的房间高3M,他打算在四周墙中涂上涂料美化居室,从地面算起,涂到多高时才使人感到舒适?
2.在人体下半身与身高的比例上,越接近0.618,越给人美感,遗憾的是,即使是身体修长的芭蕾舞演员也达不到如此的完美。某女士身高1.68米,下半身1.02米,她应该选择多高的高跟鞋看起来更美呢?
八、读一读 神奇的0.618打开地图,你就会发现那些好茶产地大多位于北纬30度左右。特别是红茶中的极品“祁红”,产地在安徽的祁门,也恰好在此纬度上。这不免让人联想起许多与北纬30度有关的地方。奇石异峰,名川秀水的黄山,庐山,九寨沟等等。衔远山,吞长江的中国三大淡水湖也恰好在这黄金分割的纬度上。 蝴蝶身长与双翅展开后的长度之比, 普通树叶的宽与长之比也接近0.618;
节目主持人报幕,绝对不会站在舞台的中央,而总是站在舞台的1/3处,站在舞台上侧近于0.618的位置才是最佳的位置;
生活中用的纸为黄金矩形,这样的长方形让人看起来舒服顺眼,正规裁法得到的纸张,不管其大小,如对于8开、16开、32开等,都仍然是近似的黄金矩形。九、谈谈感受 清点收获
2.线段的比例中项与数的比例中项的区别;1.比例中项的概念.3.什么是黄金分割.
4.如何去确定黄金分割点或黄金比.
5.用数学美去装点和美化生活.十、布置作业 : 课本P102 1、3、4、5课外作业:请同学们收集建筑、雕刻和自然界的黄金分割知识象一艘船
让它载着我们
驶向理想的 ……谢谢合作再见
, 则b就
叫a,c的比例中项用符号语言表示为:定义: 例题分析 例1. (1) 1是不是 和的比例中项?如果是比例中项,请写出相应的比例式.
(2) 2和8的比例中项是________温馨提示:线段比例中项与数的比例中项是两个不同的概念,前者是一个正数,而后者是一对互为相反数.
1.求下列线段a、b的比例中项.(1)a=3,b=27; 课内练习:±4FA= BF=∴1.422.3 二、探索交流
点F:线段AB的黄金分割点利用一元二次方程的知识,可以求出黄金比的数值几,即 的值设AB=a, AP=xxa-x历史上,人们视黄金分割为“最美丽”的几何比率。 她的上半身(以肚脐眼为分界点)和下半身的比值接近0.618. 世界艺术珍品——维纳斯女神, 她是西元前一百多年希腊雕塑鼎盛时期的代表作,请你欣赏 感受匀称 协调之美欣赏之一:芭蕾舞欣赏之二:
468m289.2m上海东方明珠电视塔高468m,上球体到塔底的距离约为289.2m, 289.2与468的比值是一个神奇的数字,这个塔的设计精巧,外型匀称、漂亮、美观、大方.欣赏之三:上海东方明珠塔例3.已知点C是线段AB的黄金分割点,且AC>CB则下列等式成立的是( )
(A) AB2=AC?CB (B) CB2=AC?AB
(C) AC2=CB?AB (D) AC2=AB?BC
例题分析例4.如图,点P是线段AB的黄金分割点,且AP>BP(1)请写出黄金分割的比例式,并指出比例中项(3)若AB=2,求PBD1.经过点B作BD⊥AB,使2.连接AD,在AD上截取DE=DB.3.在AB上截取AC=AE.你能验证这个结论吗?相信你完成下列两个小题后就会有答案.三、动手画一画 找黄金分割点已知线段AB=a,用直尺和圆规作出它的黄金分割点作法:2.请计算1.如果设AB=1,那BD,AD,AC,BC分别等于多少?点C就是所求线段AB的黄金分割点黄金分割的深远意义
历史上,人们视黄金分割为“最美丽”的几何比率,广泛应用于建筑和雕刻中,如古代希腊的帕特农神庙、埃及金字塔、上海东方明珠塔等,一些长方形的画框,宽与长之比也设计成0.618,在自然界中也有很多例子,美丽的蝴蝶身长与双翅展开后的长度之比约为0.618.许多美丽的形状都与0.618这个比值有关。古希腊的一些神庙,在建筑时高和宽也是按
黄金比0.618来建立,他们认为这样的长方形
看来是较美观;其大理石柱廓,就是根据黄金
分割律分割整个神庙的.帕特农神庙五、应用新知 体验成功你能用所学的知识解释帕特农神庙建筑中所蕴含的数学道理吗?
请用所学知识回答上面的问题这时的矩形ABCD称黄金矩形1.作顶角为36°的等腰△ABC;量出
底BC与腰AB的长度,计算: ;
2.作∠B的平分线,交AC于点D,量出CD的长度,
再计算: . (精确到0.001)0.6180.618☆再作∠C的平分线,交BD于E,
△CDE也是黄金三角形……☆顶角为36°的等腰三角形称为 黄金三角形 ☆点D是线段AC的黄金分割点.六、拓展新知 七、生活中的黄金分割1.小明家的房间高3M,他打算在四周墙中涂上涂料美化居室,从地面算起,涂到多高时才使人感到舒适?
2.在人体下半身与身高的比例上,越接近0.618,越给人美感,遗憾的是,即使是身体修长的芭蕾舞演员也达不到如此的完美。某女士身高1.68米,下半身1.02米,她应该选择多高的高跟鞋看起来更美呢?
八、读一读 神奇的0.618打开地图,你就会发现那些好茶产地大多位于北纬30度左右。特别是红茶中的极品“祁红”,产地在安徽的祁门,也恰好在此纬度上。这不免让人联想起许多与北纬30度有关的地方。奇石异峰,名川秀水的黄山,庐山,九寨沟等等。衔远山,吞长江的中国三大淡水湖也恰好在这黄金分割的纬度上。 蝴蝶身长与双翅展开后的长度之比, 普通树叶的宽与长之比也接近0.618;
节目主持人报幕,绝对不会站在舞台的中央,而总是站在舞台的1/3处,站在舞台上侧近于0.618的位置才是最佳的位置;
生活中用的纸为黄金矩形,这样的长方形让人看起来舒服顺眼,正规裁法得到的纸张,不管其大小,如对于8开、16开、32开等,都仍然是近似的黄金矩形。九、谈谈感受 清点收获
2.线段的比例中项与数的比例中项的区别;1.比例中项的概念.3.什么是黄金分割.
4.如何去确定黄金分割点或黄金比.
5.用数学美去装点和美化生活.十、布置作业 : 课本P102 1、3、4、5课外作业:请同学们收集建筑、雕刻和自然界的黄金分割知识象一艘船
让它载着我们
驶向理想的 ……谢谢合作再见
同课章节目录
