1.5三角形全等的判断(SSS)同步练习
文档属性
| 名称 | 1.5三角形全等的判断(SSS)同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 238.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-07 23:41:03 | ||
图片预览

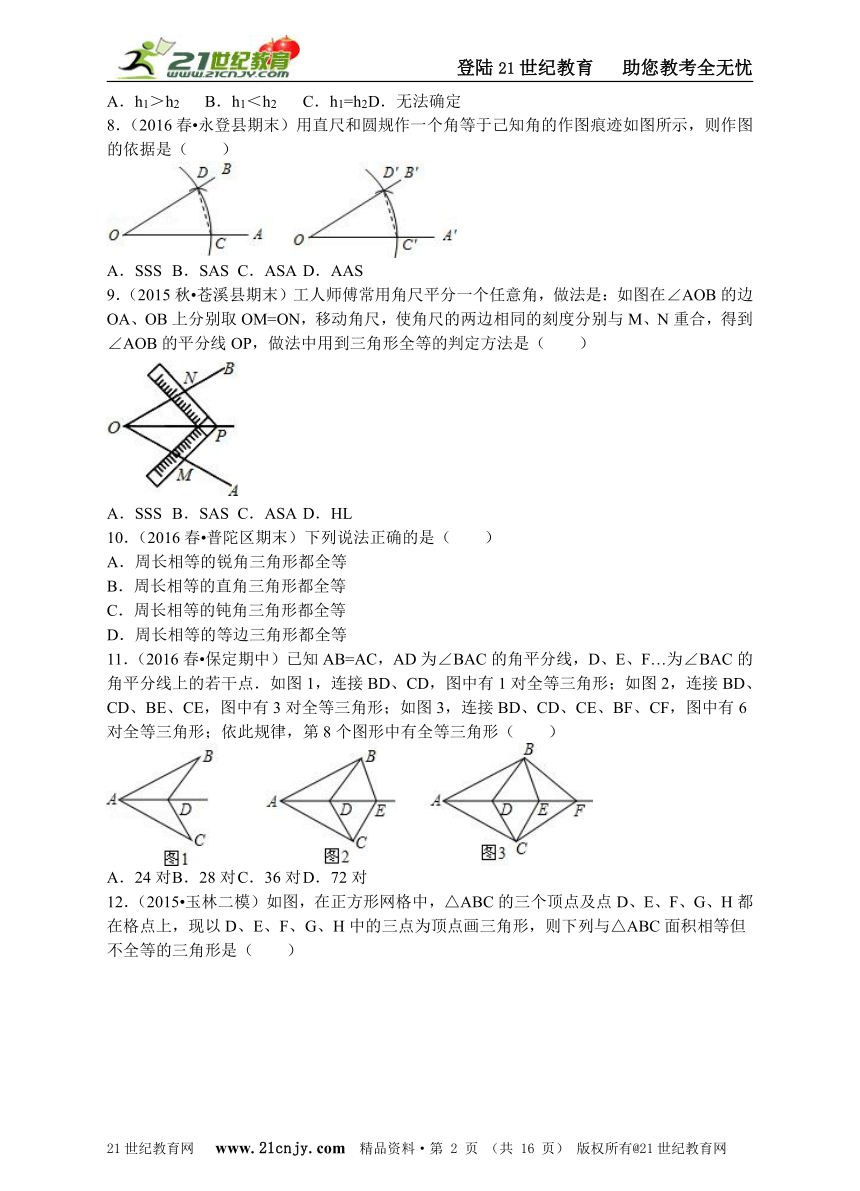
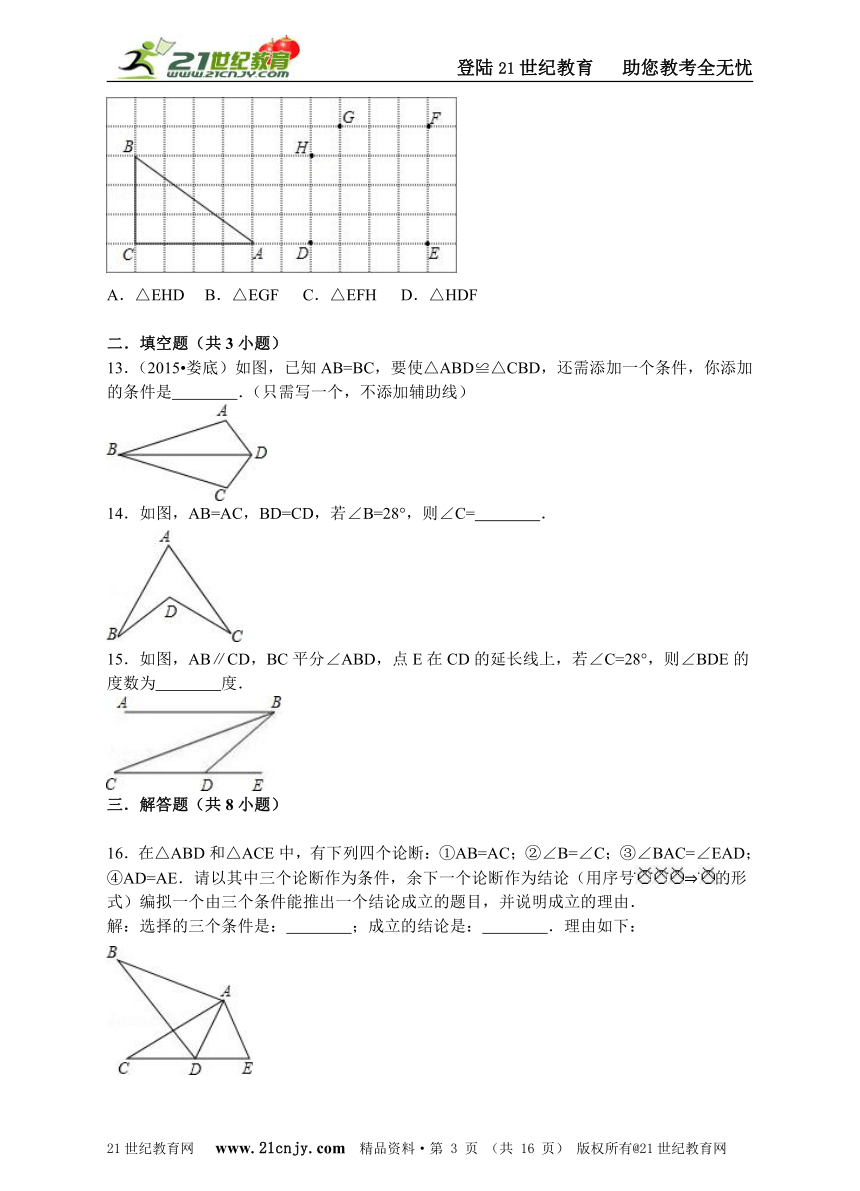
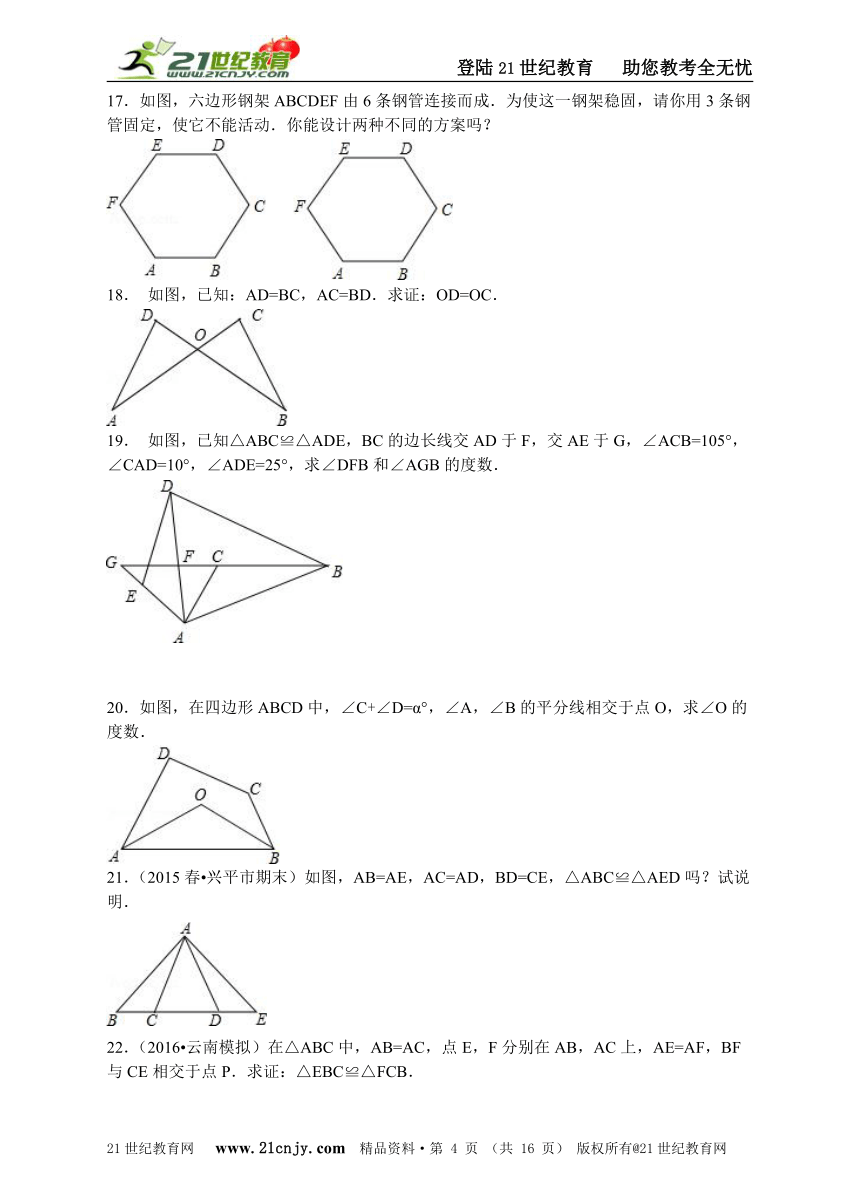

文档简介
2016年09月06日好学习的初中数学组卷
一.选择题(共12小题)
1.(2015秋?武平县校级月考)如图,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,BC、DE相交于点F,则∠DFB的度数是( )21*cnjy*com
A.15° B.20° C.25° D.30°
2.下列命题中,正确的是( )
A.三条边对应相等的两个三角形全等
B.周长相等的两个三角形全等
C.三个角对应相等的两个三角形全等
D.面积相等的两个三角形全等
3.下列判断两个三角形全等的条件中,正确的是( )
A.一条边对应相等 B.两条边对应相等
C.三个角对应相等 D.三条边对应相等
4.长为3cm,4cm,6cm,8cm的木条各两根,小明与小刚分别取了3cm和4cm的两根,要使两人所拿的三根木条组成的两个三角形全等,则他俩取的第三根木条应为( )
A.一个人取6cm的木条,一个人取8cm的木条
B.两人都取6cm的木条
C.两人都取8cm的木条
D.C两种取法都可以
5.如图,把图形沿BC对折,点A和点D重合,那么图中共有全等三角形( )
A.1对 B.2对 C.3对 D.4对
6.到三角形三边的距离相等的点是三角形的( )
A.三条边上的高的交点 B.三个内角平分线的交点
C.三边上的中线的交点 D.以上结论都不正确
7.如图,△ABC中BC边上的高为h1,△DEF中DE边上的高为h2,下列结论正确的是( )
A.h1>h2 B.h1<h2 C.h1=h2 D.无法确定
8.(2016春?永登县期末)用直尺和圆规作一个角等于己知角的作图痕迹如图所示,则作图的依据是( )21教育网
A.SSS B.SAS C.ASA D.AAS
9.(2015秋?苍溪县期末)工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA、OB上分别取OM=ON,移动角尺,使角尺的两边相同的刻度分别与M、N重合,得到∠AOB的平分线OP,做法中用到三角形全等的判定方法是( )
A.SSS B.SAS C.ASA D.HL
10.(2016春?普陀区期末)下列说法正确的是( )
A.周长相等的锐角三角形都全等
B.周长相等的直角三角形都全等
C.周长相等的钝角三角形都全等
D.周长相等的等边三角形都全等
11.(2016春?保定期中)已知AB=AC,AD为∠BAC的角平分线,D、E、F…为∠BAC的角平分线上的若干点.如图1,连接BD、CD,图中有1对全等三角形;如图2,连接BD、CD、BE、CE,图中有3对全等三角形;如图3,连接BD、CD、CE、BF、CF,图中有6对全等三角形;依此规律,第8个图形中有全等三角形( )
A.24对 B.28对 C.36对 D.72对
12.(2015?玉林二模)如图,在正方形网格中,△ABC的三个顶点及点D、E、F、G、H都在格点上,现以D、E、F、G、H中的三点为顶点画三角形,则下列与△ABC面积相等但不全等的三角形是( )www.21-cn-jy.com
A.△EHD B.△EGF C.△EFH D.△HDF
二.填空题(共3小题)
13.(2015?娄底)如图,已知AB=BC,要使△ABD≌△CBD,还需添加一个条件,你添加的条件是 .(只需写一个,不添加辅助线)【来源:21·世纪·教育·网】
14.如图,AB=AC,BD=CD,若∠B=28°,则∠C= .
15.如图,AB∥CD,BC平分∠ABD,点E在CD的延长线上,若∠C=28°,则∠BDE的度数为 度.
三.解答题(共8小题)
16.在△ABD和△ACE中,有下列四个论断:①AB=AC;②∠B=∠C;③∠BAC=∠EAD;④AD=AE.请以其中三个论断作为条件,余下一个论断作为结论(用序号?的形式)编拟一个由三个条件能推出一个结论成立的题目,并说明成立的理由.
解:选择的三个条件是: ;成立的结论是: .理由如下:
17.如图,六边形钢架ABCDEF由6条钢管连接而成.为使这一钢架稳固,请你用3条钢管固定,使它不能活动.你能设计两种不同的方案吗?
18. 如图,已知:AD=BC,AC=BD.求证:OD=OC.
19. 如图,已知△ABC≌△ADE,BC的边长线交AD于F,交AE于G,∠ACB=105°,∠CAD=10°,∠ADE=25°,求∠DFB和∠AGB的度数.
20.如图,在四边形ABCD中,∠C+∠D=α°,∠A,∠B的平分线相交于点O,求∠O的度数.
21.(2015春?兴平市期末)如图,AB=AE,AC=AD,BD=CE,△ABC≌△AED吗?试说明.
22.(2016?云南模拟)在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:△EBC≌△FCB.
23.(2015?楚雄州校级模拟)七年级下册时,我们用画图象的方法学习了探索三角形全等的条件,我们经历了下面的过程:要画一个三角形与小明画的三角形全等,需要几个与边或角的大小有关的条件呢?一个条件、两个条件、三个条件…
想一想:
1.只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?答: (填“一定”或“不一定”)由此你得出什么结论: .
2.给出两个条件画三角形时,有三种可能的情况,如:
(1)三角形的一个内角为30°,一条边为3cm.
(2)三角形的两个内角分别为30°和50°.
(3)三角形的两条边分别为4cm,6cm.
请你从上面三种情况中,任选其中一种情况画两个图形进行研究,你所画的两个图形一定全等吗?
由此你得出什么结论: .
3.如果给出三个条件画三角形,你能说出有哪几种可能的情况,请填写表格:
答:有四种可能:三条边、三个角、两边一角和 .
(1)已知一个三角形的三个内角分别为40°、60°和80°.
那么,你画的三角形和同伴画的一定全等吗?答: (填“一定”或“不一定”)
(2)已知一个三角形的三条边分别为4cm、5cm和7cm.
那么,你画的三角形和同伴画的一定全等吗?答: (填“一定”或“不一定”)
由(1)你得出什么结论: .
由(2)你得出什么结论: .
2016年09月06日好学习的初中数学组卷
参考答案与试题解析
一.选择题(共12小题)
1.(2015秋?武平县校级月考)如图,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,BC、DE相交于点F,则∠DFB的度数是( )
A.15° B.20° C.25° D.30°
【解答】解:∵△ABC≌△ADE,
∴∠B=∠D,∠BAC=∠DAE,
又∠BAD=∠BAC﹣∠CAD,∠CAE=∠DAE﹣∠CAD,
∴∠BAD=∠CAE,
∵∠DAC=60°,∠BAE=100°,
∴∠BAD=(∠BAE﹣∠DAC)=(100°﹣60°)=20°,
在△ABG和△FDG中,∵∠B=∠D,∠AGB=∠FGD,
∴∠DFB=∠BAD=20°.
故选B.
2.下列命题中,正确的是( )
A.三条边对应相等的两个三角形全等
B.周长相等的两个三角形全等
C.三个角对应相等的两个三角形全等
D.面积相等的两个三角形全等
【解答】解:A、根据全等三角形的判定定理SSS知,三条边对应相等的两个三角形全等.故本选项正确;
B、全等三角形的周长相等,但周长的两个三角形不一定能重合,不一定是全等三角形.故本选项错误;
C、AAA不能判定这两个三角形全等;故本选项错误;
D、全等三角形面积相等,但面积相等的两个三角形不一定是全等三角形.故本选项错误;
故选A.
3.下列判断两个三角形全等的条件中,正确的是( )
A.一条边对应相等 B.两条边对应相等
C.三个角对应相等 D.三条边对应相等
【解答】解:判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
故只有D符合SSS能判定三角形全等.
故选D.
4.长为3cm,4cm,6cm,8cm的木条各两根,小明与小刚分别取了3cm和4cm的两根,要使两人所拿的三根木条组成的两个三角形全等,则他俩取的第三根木条应为( )
A.一个人取6cm的木条,一个人取8cm的木条
B.两人都取6cm的木条
C.两人都取8cm的木条
D.C两种取法都可以
【解答】解:若两人所拿的三角形全等,那么两人所拿的第三根木条长度相同,故排除A;
若取8cm的木条,那么3+4<8,不能构成三角形,所以只能取6cm的木条,故排除C、D;
故选B.
5.如图,把图形沿BC对折,点A和点D重合,那么图中共有全等三角形( )
A.1对 B.2对 C.3对 D.4对
【解答】解:有△ABC≌△DBC;△ABE≌△DBE;△AEC≌△DEC.
故选C.
6.到三角形三边的距离相等的点是三角形的( )
A.三条边上的高的交点 B.三个内角平分线的交点
C.三边上的中线的交点 D.以上结论都不正确
【解答】解:到三角形三边的距离相等的点是三角形的三个内角平分线的交点.
故选B.
7.如图,△ABC中BC边上的高为h1,△DEF中DE边上的高为h2,下列结论正确的是( )
A.h1>h2 B.h1<h2 C.h1=h2 D.无法确定
【解答】解:过点A作AM⊥BC交BC于点M,过点F作FN⊥DE交DE的延长线于点N,则有AM=h1,FN=h2;21世纪教育网版权所有
在△AMC和△FNE中,
∵AM⊥BC,FN⊥DE,
∴∠AMC=∠FNE;
∵∠FED=115°,
∴∠FEN=65°=∠ACB;
∵又AC=FE,
∴△AMC≌△FNE;
∴AM=FN,
∴h1=h2.
故选C.
8.(2016春?永登县期末)用直尺和圆规作一个角等于己知角的作图痕迹如图所示,则作图的依据是( )21cnjy.com
A.SSS B.SAS C.ASA D.AAS
【解答】解:由作法易得OD=O′D',OC=0′C',CD=C′D',那么△OCD≌△O′C′D′,可得∠A′O′B′=∠AOB,所以利用的条件为SSS.2·1·c·n·j·y
故选:A.
9.(2015秋?苍溪县期末)工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA、OB上分别取OM=ON,移动角尺,使角尺的两边相同的刻度分别与M、N重合,得到∠AOB的平分线OP,做法中用到三角形全等的判定方法是( )
A.SSS B.SAS C.ASA D.HL
【解答】解﹕做法中用到的三角形全等的判定方法是SSS
证明如下
∵OM=ON
PM=PN
OP=OP
∴△ONP≌△OMP(SSS)
所以∠NOP=∠MOP
故OP为∠AOB的平分线.
故选:A.
10.(2016春?普陀区期末)下列说法正确的是( )
A.周长相等的锐角三角形都全等
B.周长相等的直角三角形都全等
C.周长相等的钝角三角形都全等
D.周长相等的等边三角形都全等
【解答】解:周长相等的锐角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项A错误;
周长相等的直角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项B错误;
周长相等的钝角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项C错误;
周长相等的锐等边三角形一定全等,因为周长相等,三条边一定对应相等,利用SSS,可以说明两个三角形全等,故选项D正确;www-2-1-cnjy-com
故选D.
11.(2016春?保定期中)已知AB=AC,AD为∠BAC的角平分线,D、E、F…为∠BAC的角平分线上的若干点.如图1,连接BD、CD,图中有1对全等三角形;如图2,连接BD、CD、BE、CE,图中有3对全等三角形;如图3,连接BD、CD、CE、BF、CF,图中有6对全等三角形;依此规律,第8个图形中有全等三角形( )
A.24对 B.28对 C.36对 D.72对
【解答】解:当有1点D时,有1对全等三角形;
当有2点D、E时,有3对全等三角形;
当有3点D、E、F时,有6对全等三角形;
当有4点时,有10个全等三角形;
…
当有n个点时,图中有个全等三角形.
则有8个点,即第8个图形中有全等三角形:=36(对).
故选:C.
12.(2015?玉林二模)如图,在正方形网格中,△ABC的三个顶点及点D、E、F、G、H都在格点上,现以D、E、F、G、H中的三点为顶点画三角形,则下列与△ABC面积相等但不全等的三角形是( )2-1-c-n-j-y
A.△EHD B.△EGF C.△EFH D.△HDF
【解答】解:A、△EHD与△ABC全等,故此选项不合题意;
B、△EGF与△ABC全等,故此选项不合题意;
C、△EFH与△ABC不全等,但是面积也不相等,故此选项不合题意;
D、△HDF与△ABC不全等,面积相等,故此选项符合题意;
故选:D.
填空题(共3小题)
13.(2015?娄底)如图,已知AB=BC,要使△ABD≌△CBD,还需添加一个条件,你添加的条件是∠ABD=∠CBD或AD=CD..(只需写一个,不添加辅助线)
【解答】解:答案不唯一.
①∠ABD=∠CBD.
在△ABD和△CBD中,
∵,
∴△ABD≌△CBD(SAS);
②AD=CD.
在△ABD和△CBD中,
∵,
∴△ABD≌△CBD(SSS).
故答案为:∠ABD=∠CBD或AD=CD.
14.如图,AB=AC,BD=CD,若∠B=28°,则∠C=28°.
【解答】解:连接线段AD
在△ABD与△ACD中,?△ABD≌△ACD?∠B=∠C
又∵∠B=28°
∴∠C=28°
故答案为28°
15.(2009?石家庄校级模拟)如图,AB∥CD,BC平分∠ABD,点E在CD的延长线上,若∠C=28°,则∠BDE的度数为56度. 21*cnjy*com
【解答】解:∵AB∥CD,
∴∠ABC=∠C,
∵BC平分∠ABD,
∴∠DBC=∠ABC,
∴∠C=∠CBD,
在△BCD中,∠BDE=2∠C=2×28°=56°.
故填空答案:56.
三.解答题(共8小题)
16.在△ABD和△ACE中,有下列四个论断:①AB=AC;②∠B=∠C;③∠BAC=∠EAD;④AD=AE.请以其中三个论断作为条件,余下一个论断作为结论(用序号?的形式)编拟一个由三个条件能推出一个结论成立的题目,并说明成立的理由.
解:选择的三个条件是:①③④;成立的结论是:②.理由如下:
【解答】解:∵∠BAC=∠EAD,
∴∠BAC+∠CAD=∠EAD+∠DAC.
即∠BAD=∠CAE.
∵AB=AC,AD=AE,
∴△BAD≌△CAE.
∴∠B=∠C.
故填:①③④;②.
17.如图,六边形钢架ABCDEF由6条钢管连接而成.为使这一钢架稳固,请你用3条钢管固定,使它不能活动.你能设计两种不同的方案吗?【出处:21教育名师】
【解答】解:答案不唯一,如图:
18. 如图,已知:AD=BC,AC=BD.求证:OD=OC.
【解答】证明:连接CD,
∵AD=BC,AC=BD,CD=CD,
∴△ACD≌△BDC(SSS)
∴∠ACD=∠BDC,
∴OD=OC.(等角对等边)
19. 如图,已知△ABC≌△ADE,BC的边长线交AD于F,交AE于G,∠ACB=105°,∠CAD=10°,∠ADE=25°,求∠DFB和∠AGB的度数.【版权所有:21教育】
【解答】解:∵△ABC≌△ADE,
∴∠ACB=∠AED,∠ABC=∠ADE,∠CAB=∠EAD.
∵∠ADE=25°,
∴∠ABC=∠ADE=25°.
∵∠ACB=105°,
∴∠CAB=180°﹣105°﹣25°=50°.
∴∠DFB=∠DAB+∠ABC=50°+10°+25°=85°.
∠AGB=∠ACB﹣∠GAC=105°﹣50°﹣10°=45°.
20.如图,在四边形ABCD中,∠C+∠D=α°,∠A,∠B的平分线相交于点O,求∠O的度数.
【解答】解:∵四边形的内角和为360°,
∴∠A+∠B=360°﹣(∠C+∠D)=360°﹣α°,
又∵OA,OB分别是两角的角平分线,
∴∠OAB+∠OBA=(∠A+∠B)=(360°﹣α°)=180°﹣,
∴∠O=180°﹣(∠OAB+∠OBA)=180°﹣(180°﹣)=.
21.(2015春?兴平市期末)如图,AB=AE,AC=AD,BD=CE,△ABC≌△AED吗?试说明.21·cn·jy·com
【解答】△ABC≌△AED,
证明:∵BD=CE,
∴BC=ED,
在△ABC和△AED中,
,
∴△ABC≌△AED.
22.(2016?云南模拟)在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:△EBC≌△FCB.【来源:21cnj*y.co*m】
【解答】证明:∵AB=AC,
∴∠ABC=∠ACB,
∵AE=AF,
∴AB﹣AE=AC﹣AF
即BE=CF,
在△EBC和△FCB中,,
∴△EBC≌△FCB(SAS).
23.(2015?楚雄州校级模拟)七年级下册时,我们用画图象的方法学习了探索三角形全等的条件,我们经历了下面的过程:要画一个三角形与小明画的三角形全等,需要几个与边或角的大小有关的条件呢?一个条件、两个条件、三个条件…21·世纪*教育网
想一想:
1.只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?答:不一定 (填“一定”或“不一定”)由此你得出什么结论:如果两个三角形有一个相等的边或角,那么这两三角形不一定全等.21教育名师原创作品
2.给出两个条件画三角形时,有三种可能的情况,如:
(1)三角形的一个内角为30°,一条边为3cm.
(2)三角形的两个内角分别为30°和50°.
(3)三角形的两条边分别为4cm,6cm.
请你从上面三种情况中,任选其中一种情况画两个图形进行研究,你所画的两个图形一定全等吗?
由此你得出什么结论:两个三角形的边或角中,如果有两个相等,那么这两个三角形不一定全等.
3.如果给出三个条件画三角形,你能说出有哪几种可能的情况,请填写表格:
答:有四种可能:三条边、三个角、两边一角和两角一边.
(1)已知一个三角形的三个内角分别为40°、60°和80°.
那么,你画的三角形和同伴画的一定全等吗?答:不一定(填“一定”或“不一定”)
(2)已知一个三角形的三条边分别为4cm、5cm和7cm.
那么,你画的三角形和同伴画的一定全等吗?答:一定(填“一定”或“不一定”)
由(1)你得出什么结论:有三角分别相等的两个三角形不一定全等.
由(2)你得出什么结论:有三边分别相等的两个三角形全等.
【解答】解:1.如图1,
△ACD和△ABC的边AC=AC,但是两三角形不全等,
故答案为;不一定,如果两个三角形有一个相等的边或角,那么这两个三角形不一定全等;
2.(1)如图2,
∠A=∠A=30°,BC=BD=3cm,
但是△ABC和△ABD补全等,
即如果两个三角形有两个相等的边或角,那么这两个三角形不一定全等,
故答案为:两个三角形的边或角中,如果有两个相等,那么这两个三角形不一定全等;
3.
故答案:两角一边;
(1)如图3,
△ADE和△ABC中,∠A=∠A=40°,∠ADE=∠B=60°,∠AED=∠ACB,
但是两三角形不全等,
故答案为:不一定;
(2)如图4,
△ABC和△DEF中,AC=DF=4cm,AB=DE=5cm,BC=FE=7cm,
则△ABC≌△DEF,
故答案为:一定,有三角分别相等的两个三角形不一定全等,有三边分别相等的两个三角形全等.
一.选择题(共12小题)
1.(2015秋?武平县校级月考)如图,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,BC、DE相交于点F,则∠DFB的度数是( )21*cnjy*com
A.15° B.20° C.25° D.30°
2.下列命题中,正确的是( )
A.三条边对应相等的两个三角形全等
B.周长相等的两个三角形全等
C.三个角对应相等的两个三角形全等
D.面积相等的两个三角形全等
3.下列判断两个三角形全等的条件中,正确的是( )
A.一条边对应相等 B.两条边对应相等
C.三个角对应相等 D.三条边对应相等
4.长为3cm,4cm,6cm,8cm的木条各两根,小明与小刚分别取了3cm和4cm的两根,要使两人所拿的三根木条组成的两个三角形全等,则他俩取的第三根木条应为( )
A.一个人取6cm的木条,一个人取8cm的木条
B.两人都取6cm的木条
C.两人都取8cm的木条
D.C两种取法都可以
5.如图,把图形沿BC对折,点A和点D重合,那么图中共有全等三角形( )
A.1对 B.2对 C.3对 D.4对
6.到三角形三边的距离相等的点是三角形的( )
A.三条边上的高的交点 B.三个内角平分线的交点
C.三边上的中线的交点 D.以上结论都不正确
7.如图,△ABC中BC边上的高为h1,△DEF中DE边上的高为h2,下列结论正确的是( )
A.h1>h2 B.h1<h2 C.h1=h2 D.无法确定
8.(2016春?永登县期末)用直尺和圆规作一个角等于己知角的作图痕迹如图所示,则作图的依据是( )21教育网
A.SSS B.SAS C.ASA D.AAS
9.(2015秋?苍溪县期末)工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA、OB上分别取OM=ON,移动角尺,使角尺的两边相同的刻度分别与M、N重合,得到∠AOB的平分线OP,做法中用到三角形全等的判定方法是( )
A.SSS B.SAS C.ASA D.HL
10.(2016春?普陀区期末)下列说法正确的是( )
A.周长相等的锐角三角形都全等
B.周长相等的直角三角形都全等
C.周长相等的钝角三角形都全等
D.周长相等的等边三角形都全等
11.(2016春?保定期中)已知AB=AC,AD为∠BAC的角平分线,D、E、F…为∠BAC的角平分线上的若干点.如图1,连接BD、CD,图中有1对全等三角形;如图2,连接BD、CD、BE、CE,图中有3对全等三角形;如图3,连接BD、CD、CE、BF、CF,图中有6对全等三角形;依此规律,第8个图形中有全等三角形( )
A.24对 B.28对 C.36对 D.72对
12.(2015?玉林二模)如图,在正方形网格中,△ABC的三个顶点及点D、E、F、G、H都在格点上,现以D、E、F、G、H中的三点为顶点画三角形,则下列与△ABC面积相等但不全等的三角形是( )www.21-cn-jy.com
A.△EHD B.△EGF C.△EFH D.△HDF
二.填空题(共3小题)
13.(2015?娄底)如图,已知AB=BC,要使△ABD≌△CBD,还需添加一个条件,你添加的条件是 .(只需写一个,不添加辅助线)【来源:21·世纪·教育·网】
14.如图,AB=AC,BD=CD,若∠B=28°,则∠C= .
15.如图,AB∥CD,BC平分∠ABD,点E在CD的延长线上,若∠C=28°,则∠BDE的度数为 度.
三.解答题(共8小题)
16.在△ABD和△ACE中,有下列四个论断:①AB=AC;②∠B=∠C;③∠BAC=∠EAD;④AD=AE.请以其中三个论断作为条件,余下一个论断作为结论(用序号?的形式)编拟一个由三个条件能推出一个结论成立的题目,并说明成立的理由.
解:选择的三个条件是: ;成立的结论是: .理由如下:
17.如图,六边形钢架ABCDEF由6条钢管连接而成.为使这一钢架稳固,请你用3条钢管固定,使它不能活动.你能设计两种不同的方案吗?
18. 如图,已知:AD=BC,AC=BD.求证:OD=OC.
19. 如图,已知△ABC≌△ADE,BC的边长线交AD于F,交AE于G,∠ACB=105°,∠CAD=10°,∠ADE=25°,求∠DFB和∠AGB的度数.
20.如图,在四边形ABCD中,∠C+∠D=α°,∠A,∠B的平分线相交于点O,求∠O的度数.
21.(2015春?兴平市期末)如图,AB=AE,AC=AD,BD=CE,△ABC≌△AED吗?试说明.
22.(2016?云南模拟)在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:△EBC≌△FCB.
23.(2015?楚雄州校级模拟)七年级下册时,我们用画图象的方法学习了探索三角形全等的条件,我们经历了下面的过程:要画一个三角形与小明画的三角形全等,需要几个与边或角的大小有关的条件呢?一个条件、两个条件、三个条件…
想一想:
1.只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?答: (填“一定”或“不一定”)由此你得出什么结论: .
2.给出两个条件画三角形时,有三种可能的情况,如:
(1)三角形的一个内角为30°,一条边为3cm.
(2)三角形的两个内角分别为30°和50°.
(3)三角形的两条边分别为4cm,6cm.
请你从上面三种情况中,任选其中一种情况画两个图形进行研究,你所画的两个图形一定全等吗?
由此你得出什么结论: .
3.如果给出三个条件画三角形,你能说出有哪几种可能的情况,请填写表格:
答:有四种可能:三条边、三个角、两边一角和 .
(1)已知一个三角形的三个内角分别为40°、60°和80°.
那么,你画的三角形和同伴画的一定全等吗?答: (填“一定”或“不一定”)
(2)已知一个三角形的三条边分别为4cm、5cm和7cm.
那么,你画的三角形和同伴画的一定全等吗?答: (填“一定”或“不一定”)
由(1)你得出什么结论: .
由(2)你得出什么结论: .
2016年09月06日好学习的初中数学组卷
参考答案与试题解析
一.选择题(共12小题)
1.(2015秋?武平县校级月考)如图,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,BC、DE相交于点F,则∠DFB的度数是( )
A.15° B.20° C.25° D.30°
【解答】解:∵△ABC≌△ADE,
∴∠B=∠D,∠BAC=∠DAE,
又∠BAD=∠BAC﹣∠CAD,∠CAE=∠DAE﹣∠CAD,
∴∠BAD=∠CAE,
∵∠DAC=60°,∠BAE=100°,
∴∠BAD=(∠BAE﹣∠DAC)=(100°﹣60°)=20°,
在△ABG和△FDG中,∵∠B=∠D,∠AGB=∠FGD,
∴∠DFB=∠BAD=20°.
故选B.
2.下列命题中,正确的是( )
A.三条边对应相等的两个三角形全等
B.周长相等的两个三角形全等
C.三个角对应相等的两个三角形全等
D.面积相等的两个三角形全等
【解答】解:A、根据全等三角形的判定定理SSS知,三条边对应相等的两个三角形全等.故本选项正确;
B、全等三角形的周长相等,但周长的两个三角形不一定能重合,不一定是全等三角形.故本选项错误;
C、AAA不能判定这两个三角形全等;故本选项错误;
D、全等三角形面积相等,但面积相等的两个三角形不一定是全等三角形.故本选项错误;
故选A.
3.下列判断两个三角形全等的条件中,正确的是( )
A.一条边对应相等 B.两条边对应相等
C.三个角对应相等 D.三条边对应相等
【解答】解:判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
故只有D符合SSS能判定三角形全等.
故选D.
4.长为3cm,4cm,6cm,8cm的木条各两根,小明与小刚分别取了3cm和4cm的两根,要使两人所拿的三根木条组成的两个三角形全等,则他俩取的第三根木条应为( )
A.一个人取6cm的木条,一个人取8cm的木条
B.两人都取6cm的木条
C.两人都取8cm的木条
D.C两种取法都可以
【解答】解:若两人所拿的三角形全等,那么两人所拿的第三根木条长度相同,故排除A;
若取8cm的木条,那么3+4<8,不能构成三角形,所以只能取6cm的木条,故排除C、D;
故选B.
5.如图,把图形沿BC对折,点A和点D重合,那么图中共有全等三角形( )
A.1对 B.2对 C.3对 D.4对
【解答】解:有△ABC≌△DBC;△ABE≌△DBE;△AEC≌△DEC.
故选C.
6.到三角形三边的距离相等的点是三角形的( )
A.三条边上的高的交点 B.三个内角平分线的交点
C.三边上的中线的交点 D.以上结论都不正确
【解答】解:到三角形三边的距离相等的点是三角形的三个内角平分线的交点.
故选B.
7.如图,△ABC中BC边上的高为h1,△DEF中DE边上的高为h2,下列结论正确的是( )
A.h1>h2 B.h1<h2 C.h1=h2 D.无法确定
【解答】解:过点A作AM⊥BC交BC于点M,过点F作FN⊥DE交DE的延长线于点N,则有AM=h1,FN=h2;21世纪教育网版权所有
在△AMC和△FNE中,
∵AM⊥BC,FN⊥DE,
∴∠AMC=∠FNE;
∵∠FED=115°,
∴∠FEN=65°=∠ACB;
∵又AC=FE,
∴△AMC≌△FNE;
∴AM=FN,
∴h1=h2.
故选C.
8.(2016春?永登县期末)用直尺和圆规作一个角等于己知角的作图痕迹如图所示,则作图的依据是( )21cnjy.com
A.SSS B.SAS C.ASA D.AAS
【解答】解:由作法易得OD=O′D',OC=0′C',CD=C′D',那么△OCD≌△O′C′D′,可得∠A′O′B′=∠AOB,所以利用的条件为SSS.2·1·c·n·j·y
故选:A.
9.(2015秋?苍溪县期末)工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA、OB上分别取OM=ON,移动角尺,使角尺的两边相同的刻度分别与M、N重合,得到∠AOB的平分线OP,做法中用到三角形全等的判定方法是( )
A.SSS B.SAS C.ASA D.HL
【解答】解﹕做法中用到的三角形全等的判定方法是SSS
证明如下
∵OM=ON
PM=PN
OP=OP
∴△ONP≌△OMP(SSS)
所以∠NOP=∠MOP
故OP为∠AOB的平分线.
故选:A.
10.(2016春?普陀区期末)下列说法正确的是( )
A.周长相等的锐角三角形都全等
B.周长相等的直角三角形都全等
C.周长相等的钝角三角形都全等
D.周长相等的等边三角形都全等
【解答】解:周长相等的锐角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项A错误;
周长相等的直角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项B错误;
周长相等的钝角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项C错误;
周长相等的锐等边三角形一定全等,因为周长相等,三条边一定对应相等,利用SSS,可以说明两个三角形全等,故选项D正确;www-2-1-cnjy-com
故选D.
11.(2016春?保定期中)已知AB=AC,AD为∠BAC的角平分线,D、E、F…为∠BAC的角平分线上的若干点.如图1,连接BD、CD,图中有1对全等三角形;如图2,连接BD、CD、BE、CE,图中有3对全等三角形;如图3,连接BD、CD、CE、BF、CF,图中有6对全等三角形;依此规律,第8个图形中有全等三角形( )
A.24对 B.28对 C.36对 D.72对
【解答】解:当有1点D时,有1对全等三角形;
当有2点D、E时,有3对全等三角形;
当有3点D、E、F时,有6对全等三角形;
当有4点时,有10个全等三角形;
…
当有n个点时,图中有个全等三角形.
则有8个点,即第8个图形中有全等三角形:=36(对).
故选:C.
12.(2015?玉林二模)如图,在正方形网格中,△ABC的三个顶点及点D、E、F、G、H都在格点上,现以D、E、F、G、H中的三点为顶点画三角形,则下列与△ABC面积相等但不全等的三角形是( )2-1-c-n-j-y
A.△EHD B.△EGF C.△EFH D.△HDF
【解答】解:A、△EHD与△ABC全等,故此选项不合题意;
B、△EGF与△ABC全等,故此选项不合题意;
C、△EFH与△ABC不全等,但是面积也不相等,故此选项不合题意;
D、△HDF与△ABC不全等,面积相等,故此选项符合题意;
故选:D.
填空题(共3小题)
13.(2015?娄底)如图,已知AB=BC,要使△ABD≌△CBD,还需添加一个条件,你添加的条件是∠ABD=∠CBD或AD=CD..(只需写一个,不添加辅助线)
【解答】解:答案不唯一.
①∠ABD=∠CBD.
在△ABD和△CBD中,
∵,
∴△ABD≌△CBD(SAS);
②AD=CD.
在△ABD和△CBD中,
∵,
∴△ABD≌△CBD(SSS).
故答案为:∠ABD=∠CBD或AD=CD.
14.如图,AB=AC,BD=CD,若∠B=28°,则∠C=28°.
【解答】解:连接线段AD
在△ABD与△ACD中,?△ABD≌△ACD?∠B=∠C
又∵∠B=28°
∴∠C=28°
故答案为28°
15.(2009?石家庄校级模拟)如图,AB∥CD,BC平分∠ABD,点E在CD的延长线上,若∠C=28°,则∠BDE的度数为56度. 21*cnjy*com
【解答】解:∵AB∥CD,
∴∠ABC=∠C,
∵BC平分∠ABD,
∴∠DBC=∠ABC,
∴∠C=∠CBD,
在△BCD中,∠BDE=2∠C=2×28°=56°.
故填空答案:56.
三.解答题(共8小题)
16.在△ABD和△ACE中,有下列四个论断:①AB=AC;②∠B=∠C;③∠BAC=∠EAD;④AD=AE.请以其中三个论断作为条件,余下一个论断作为结论(用序号?的形式)编拟一个由三个条件能推出一个结论成立的题目,并说明成立的理由.
解:选择的三个条件是:①③④;成立的结论是:②.理由如下:
【解答】解:∵∠BAC=∠EAD,
∴∠BAC+∠CAD=∠EAD+∠DAC.
即∠BAD=∠CAE.
∵AB=AC,AD=AE,
∴△BAD≌△CAE.
∴∠B=∠C.
故填:①③④;②.
17.如图,六边形钢架ABCDEF由6条钢管连接而成.为使这一钢架稳固,请你用3条钢管固定,使它不能活动.你能设计两种不同的方案吗?【出处:21教育名师】
【解答】解:答案不唯一,如图:
18. 如图,已知:AD=BC,AC=BD.求证:OD=OC.
【解答】证明:连接CD,
∵AD=BC,AC=BD,CD=CD,
∴△ACD≌△BDC(SSS)
∴∠ACD=∠BDC,
∴OD=OC.(等角对等边)
19. 如图,已知△ABC≌△ADE,BC的边长线交AD于F,交AE于G,∠ACB=105°,∠CAD=10°,∠ADE=25°,求∠DFB和∠AGB的度数.【版权所有:21教育】
【解答】解:∵△ABC≌△ADE,
∴∠ACB=∠AED,∠ABC=∠ADE,∠CAB=∠EAD.
∵∠ADE=25°,
∴∠ABC=∠ADE=25°.
∵∠ACB=105°,
∴∠CAB=180°﹣105°﹣25°=50°.
∴∠DFB=∠DAB+∠ABC=50°+10°+25°=85°.
∠AGB=∠ACB﹣∠GAC=105°﹣50°﹣10°=45°.
20.如图,在四边形ABCD中,∠C+∠D=α°,∠A,∠B的平分线相交于点O,求∠O的度数.
【解答】解:∵四边形的内角和为360°,
∴∠A+∠B=360°﹣(∠C+∠D)=360°﹣α°,
又∵OA,OB分别是两角的角平分线,
∴∠OAB+∠OBA=(∠A+∠B)=(360°﹣α°)=180°﹣,
∴∠O=180°﹣(∠OAB+∠OBA)=180°﹣(180°﹣)=.
21.(2015春?兴平市期末)如图,AB=AE,AC=AD,BD=CE,△ABC≌△AED吗?试说明.21·cn·jy·com
【解答】△ABC≌△AED,
证明:∵BD=CE,
∴BC=ED,
在△ABC和△AED中,
,
∴△ABC≌△AED.
22.(2016?云南模拟)在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:△EBC≌△FCB.【来源:21cnj*y.co*m】
【解答】证明:∵AB=AC,
∴∠ABC=∠ACB,
∵AE=AF,
∴AB﹣AE=AC﹣AF
即BE=CF,
在△EBC和△FCB中,,
∴△EBC≌△FCB(SAS).
23.(2015?楚雄州校级模拟)七年级下册时,我们用画图象的方法学习了探索三角形全等的条件,我们经历了下面的过程:要画一个三角形与小明画的三角形全等,需要几个与边或角的大小有关的条件呢?一个条件、两个条件、三个条件…21·世纪*教育网
想一想:
1.只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?答:不一定 (填“一定”或“不一定”)由此你得出什么结论:如果两个三角形有一个相等的边或角,那么这两三角形不一定全等.21教育名师原创作品
2.给出两个条件画三角形时,有三种可能的情况,如:
(1)三角形的一个内角为30°,一条边为3cm.
(2)三角形的两个内角分别为30°和50°.
(3)三角形的两条边分别为4cm,6cm.
请你从上面三种情况中,任选其中一种情况画两个图形进行研究,你所画的两个图形一定全等吗?
由此你得出什么结论:两个三角形的边或角中,如果有两个相等,那么这两个三角形不一定全等.
3.如果给出三个条件画三角形,你能说出有哪几种可能的情况,请填写表格:
答:有四种可能:三条边、三个角、两边一角和两角一边.
(1)已知一个三角形的三个内角分别为40°、60°和80°.
那么,你画的三角形和同伴画的一定全等吗?答:不一定(填“一定”或“不一定”)
(2)已知一个三角形的三条边分别为4cm、5cm和7cm.
那么,你画的三角形和同伴画的一定全等吗?答:一定(填“一定”或“不一定”)
由(1)你得出什么结论:有三角分别相等的两个三角形不一定全等.
由(2)你得出什么结论:有三边分别相等的两个三角形全等.
【解答】解:1.如图1,
△ACD和△ABC的边AC=AC,但是两三角形不全等,
故答案为;不一定,如果两个三角形有一个相等的边或角,那么这两个三角形不一定全等;
2.(1)如图2,
∠A=∠A=30°,BC=BD=3cm,
但是△ABC和△ABD补全等,
即如果两个三角形有两个相等的边或角,那么这两个三角形不一定全等,
故答案为:两个三角形的边或角中,如果有两个相等,那么这两个三角形不一定全等;
3.
故答案:两角一边;
(1)如图3,
△ADE和△ABC中,∠A=∠A=40°,∠ADE=∠B=60°,∠AED=∠ACB,
但是两三角形不全等,
故答案为:不一定;
(2)如图4,
△ABC和△DEF中,AC=DF=4cm,AB=DE=5cm,BC=FE=7cm,
则△ABC≌△DEF,
故答案为:一定,有三角分别相等的两个三角形不一定全等,有三边分别相等的两个三角形全等.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
