浙教版八年级上1.6尺规作图课件(共14张ppt)
文档属性
| 名称 | 浙教版八年级上1.6尺规作图课件(共14张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-08 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
浙教版八年级 上册
据说,为了显示谁的逻辑能力更强,古希腊人限制了几何作图的工具,结果一些普通的画图题让数学家思索了2000多年.尺规作图特有的魅力,使无数人沉湎其中.
在几何作图中,我们把用没有刻度的直尺和圆规作图,简称尺规作图.
角平分线
三角形
已知:线段a,b,c.
a
b
c
求作:△ABC,使BC=a,AC=b,AB=c.
作法
(1)做线段BC=a .
(2)以C为圆心, b为半径画弧.
(3)以B为圆心, c为半径画弧,两弧相交于点A.
(4)连结AB,AC.
则△ABC为所求作的三角形.
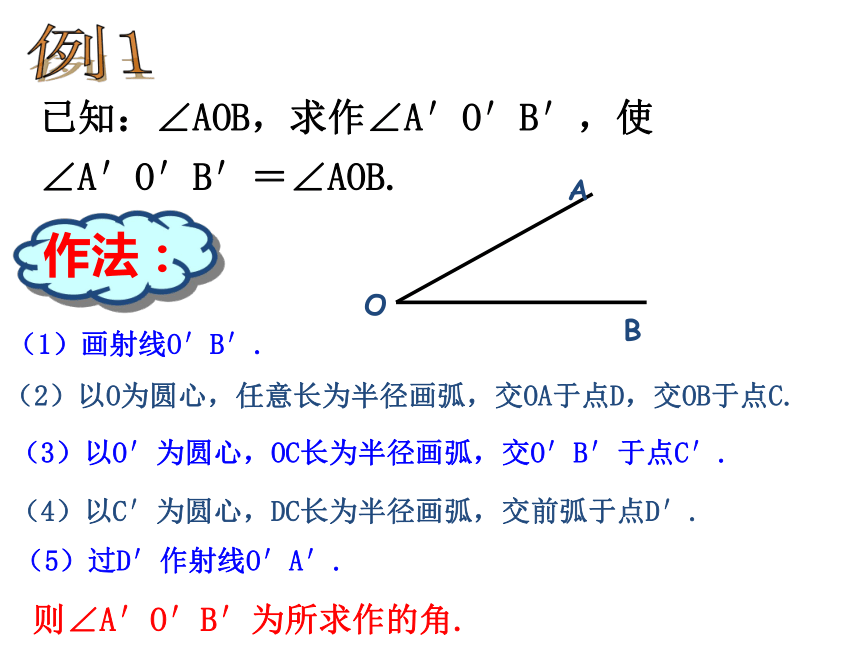
已知:∠AOB,求作∠A′O′B′,使∠A′O′B′=∠AOB.
O
B
A
(1)画射线O′B′.
(2)以O为圆心,任意长为半径画弧,交OA于点D,交OB于点C.
(3)以O′为圆心,OC长为半径画弧,交O′B′于点C′.
(4)以C′为圆心,DC长为半径画弧,交前弧于点D′.
(5)过D′作射线O′A′.
则∠A′O′B′为所求作的角.
作法:
A
B
C
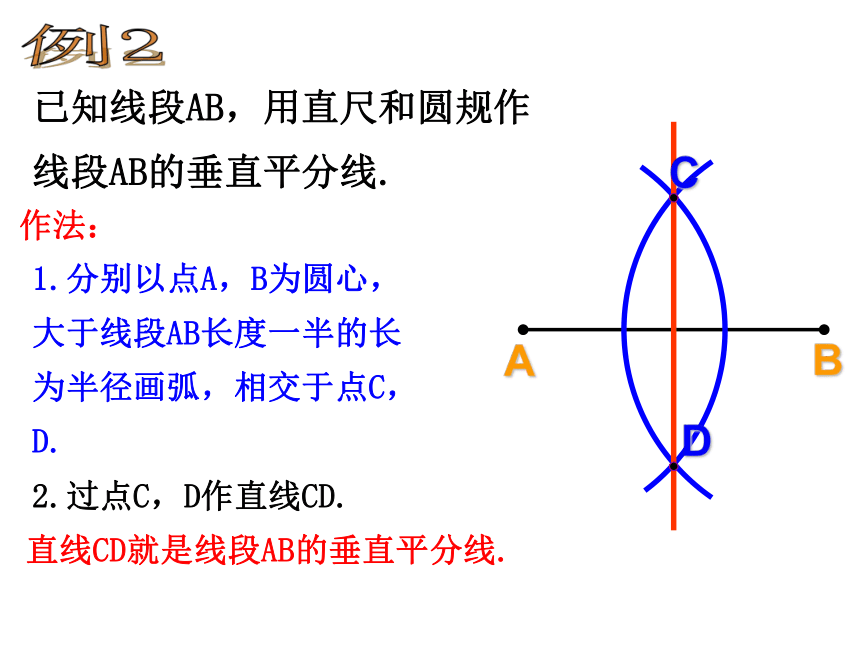
已知线段AB,用直尺和圆规作
线段AB的垂直平分线.
作法:
1.分别以点A,B为圆心,
大于线段AB长度一半的长
为半径画弧,相交于点C,D.
2.过点C,D作直线CD.
直线CD就是线段AB的垂直平分线.
D
已知:线段a,c,∠α,求作:△ABC,使BC=a,AB=c,∠ABC=∠α.
a
c
a
B
M
D
E
D′
E′
N
C
A
(1)作∠MBN=∠α.
(2)在射线BM上截取BC=a, 在射线BN上截取BA=c.
(3)连结AC.
△ABC为所求作的三角形.
作法
一般情况下,
◆已知两角夹边,先画边,再画两角;
◆已知两边夹角,先画角,再在角的
两边分别截取两边.
◆已知三边呢
如图,某人不小心把一块三角形的玻璃打碎成三块,现在要到玻璃店去配一块完全一样的玻璃,那么他最少要( ).
A、带①去
B、带②去
C、带③去
D、带①和②去
C
例3 已知∠α,∠β和线段a,用直尺和圆规作△ABC,使∠A=∠α,∠B=∠β,AB=a.
b
a
a
作法:
(1)作线段AB=a,
(2)在线段AB的同侧作∠BAX=∠α,∠ABY= ∠β,
两边相交于C;
则△ABC就是所要求作的三角形.
有 A, B ,C 三位农户准备一起挖一口井,使它到三位农户家的距离相等.这口井应挖在何处?请在图中标出井的位置,并说明理由.
A
C
B
已知∠α、∠β,求作∠ABC,使∠ABC= ∠α + ∠β .
α
β
在ABC中,BC=5厘米,AC=3厘米, AB=3.5厘米,∠B=35°,∠C=45°,请你选择适当数据,画与△ABC全等的三角形,说一说你有几种办法呢?
C
A
B
3.5厘米
5厘米
3厘米
浙教版八年级 上册
据说,为了显示谁的逻辑能力更强,古希腊人限制了几何作图的工具,结果一些普通的画图题让数学家思索了2000多年.尺规作图特有的魅力,使无数人沉湎其中.
在几何作图中,我们把用没有刻度的直尺和圆规作图,简称尺规作图.
角平分线
三角形
已知:线段a,b,c.
a
b
c
求作:△ABC,使BC=a,AC=b,AB=c.
作法
(1)做线段BC=a .
(2)以C为圆心, b为半径画弧.
(3)以B为圆心, c为半径画弧,两弧相交于点A.
(4)连结AB,AC.
则△ABC为所求作的三角形.
已知:∠AOB,求作∠A′O′B′,使∠A′O′B′=∠AOB.
O
B
A
(1)画射线O′B′.
(2)以O为圆心,任意长为半径画弧,交OA于点D,交OB于点C.
(3)以O′为圆心,OC长为半径画弧,交O′B′于点C′.
(4)以C′为圆心,DC长为半径画弧,交前弧于点D′.
(5)过D′作射线O′A′.
则∠A′O′B′为所求作的角.
作法:
A
B
C
已知线段AB,用直尺和圆规作
线段AB的垂直平分线.
作法:
1.分别以点A,B为圆心,
大于线段AB长度一半的长
为半径画弧,相交于点C,D.
2.过点C,D作直线CD.
直线CD就是线段AB的垂直平分线.
D
已知:线段a,c,∠α,求作:△ABC,使BC=a,AB=c,∠ABC=∠α.
a
c
a
B
M
D
E
D′
E′
N
C
A
(1)作∠MBN=∠α.
(2)在射线BM上截取BC=a, 在射线BN上截取BA=c.
(3)连结AC.
△ABC为所求作的三角形.
作法
一般情况下,
◆已知两角夹边,先画边,再画两角;
◆已知两边夹角,先画角,再在角的
两边分别截取两边.
◆已知三边呢
如图,某人不小心把一块三角形的玻璃打碎成三块,现在要到玻璃店去配一块完全一样的玻璃,那么他最少要( ).
A、带①去
B、带②去
C、带③去
D、带①和②去
C
例3 已知∠α,∠β和线段a,用直尺和圆规作△ABC,使∠A=∠α,∠B=∠β,AB=a.
b
a
a
作法:
(1)作线段AB=a,
(2)在线段AB的同侧作∠BAX=∠α,∠ABY= ∠β,
两边相交于C;
则△ABC就是所要求作的三角形.
有 A, B ,C 三位农户准备一起挖一口井,使它到三位农户家的距离相等.这口井应挖在何处?请在图中标出井的位置,并说明理由.
A
C
B
已知∠α、∠β,求作∠ABC,使∠ABC= ∠α + ∠β .
α
β
在ABC中,BC=5厘米,AC=3厘米, AB=3.5厘米,∠B=35°,∠C=45°,请你选择适当数据,画与△ABC全等的三角形,说一说你有几种办法呢?
C
A
B
3.5厘米
5厘米
3厘米
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
