1.6尺规作图同步练习

　
1.6尺规作图同步练习
　
一．选择题（共14小题）
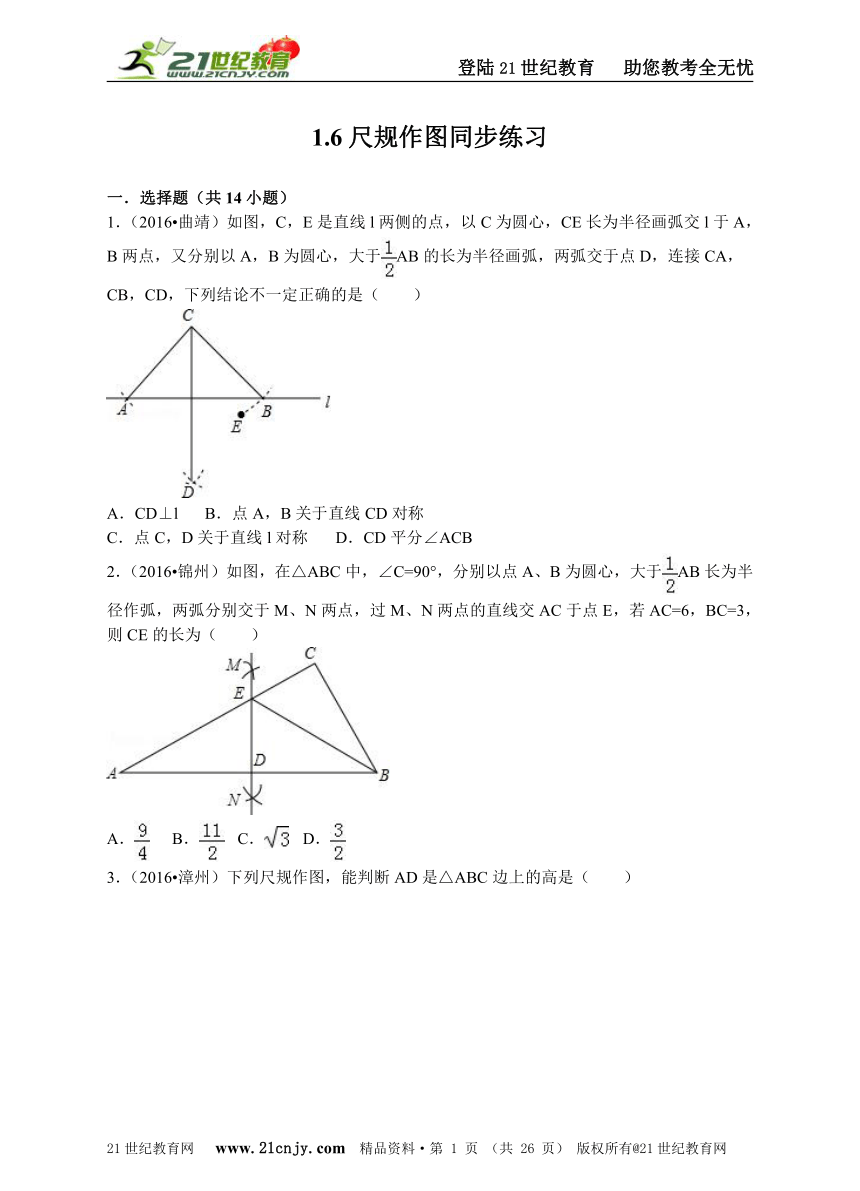
1．（2016?曲靖）如图，C，E是直线l两侧的点，以C为圆心，CE长为半径画弧交l于A，B两点，又分别以A，B为圆心，大于AB的长为半径画弧，两弧交于点D，连接CA，CB，CD，下列结论不一定正确的是（　　）
A．CD⊥l B．点A，B关于直线CD对称
C．点C，D关于直线l对称 D．CD平分∠ACB
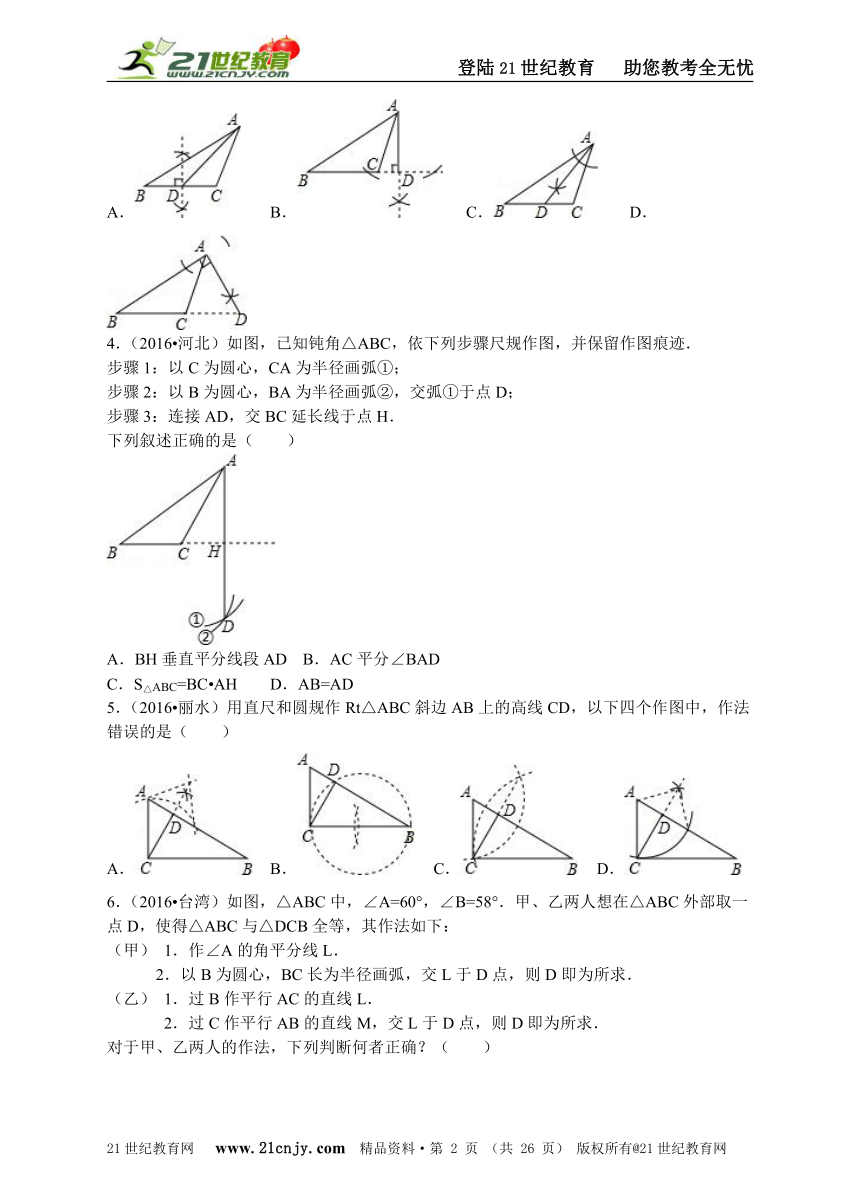
2．（2016?锦州）如图，在△ABC中，∠C=90°，分别以点A、B为圆心，大于AB长为半径作弧，两弧分别交于M、N两点，过M、N两点的直线交AC于点E，若AC=6，BC=3，则CE的长为（　　）
A． B． C． D．
3．（2016?漳州）下列尺规作图，能判断AD是△ABC边上的高是（　　）
A． B． C． D．
4．（2016?河北）如图，已知钝角△ABC，依下列步骤尺规作图，并保留作图痕迹．
步骤1：以C为圆心，CA为半径画弧①；
步骤2：以B为圆心，BA为半径画弧②，交弧①于点D；
步骤3：连接AD，交BC延长线于点H．
下列叙述正确的是（　　）
A．BH垂直平分线段AD B．AC平分∠BAD
C．S△ABC=BC?AH D．AB=AD
5．（2016?丽水）用直尺和圆规作Rt△ABC斜边AB上的高线CD，以下四个作图中，作法错误的是（　　）
A． B． C． D．
6．（2016?台湾）如图，△ABC中，∠A=60°，∠B=58°．甲、乙两人想在△ABC外部取一点D，使得△ABC与△DCB全等，其作法如下：
（甲） 1．作∠A的角平分线L．
2．以B为圆心，BC长为半径画弧，交L于D点，则D即为所求．
（乙） 1．过B作平行AC的直线L．
2．过C作平行AB的直线M，交L于D点，则D即为所求．
对于甲、乙两人的作法，下列判断何者正确？（　　）
A．两人皆正确 B．两人皆错误
C．甲正确，乙错误 D．甲错误，乙正确
7．（2016?阳泉模拟）下列关于尺规的功能说法不正确的是（　　）
A．直尺的功能是：在两点间连接一条线段，将线段向两方向延长
B．直尺的功能是：可作平角和直角
C．圆规的功能是：以任意长为半径，以任意点为圆心作一个圆
D．圆规的功能是：以任意长为半径，以任意点为圆心作一段弧
8．（2016?开平区一模）如图，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，分别交AB、AC于E、F两点；再分别以E、F为圆心，大于EF长为半径作圆弧，两条圆弧交于点G，作射线AG交CD于点H．若∠C=140°，则∠AHC的大小是（　　）
A．20° B．25° C．30° D．40°
9．（2016?柘城县一模）如图，已知△ABC，∠C=90°，按以下步骤：①分别以A、B为圆心，以大于的长为半径作弧，两弧相交于两点M、N；②作直线MN交BC于点D．若AC=1.5，∠B=15°．则BD等于（　　）
A．1.5 B．2 C．2.5 D．3
10．（2016?商丘模拟）如图，在△ABC中，AD平分∠BAC，按如下步骤作图：①分别以点A、D为圆心，以大于AD的长为半径在AD两侧作弧，交于两点M、N；②连接MN分别交AB、AC于点E、F；③连接DE、DF．若BD=6，AF=4，CD=3，则BE的长是（　　）
A．2 B．4 C．6 D．8
11．（2016?东台市二模）如图，利用尺规作的角平分线OC，在用尺规作角平分线时，用到的三角形全等的判定方法是（　　）
作法：①以O为圆心，任意长为半径作弧，交OA，OB于点D，E．
②分别以D，E为圆心，以大于DE的长为半径作弧，两弧在∠AOB内交于点C．
③作射线OC．则OC就是∠AOB的平分线．
A．SSS B．SAS C．ASA D．AAS
12．（2016?温岭市一模）“过直线外一点作已知直线的垂线”．下列尺规作图中对应的正确作法是（　　）
A． B． C． D．
13．（2016?许昌一模）如图，已知在Rt△ABC中，∠ABC=90°，点D是BC边的中点，分别以B、C为圆心，大于BC长为半径画弧，两弧在直线BC上方的交点为P，直线PD交AC于点E，连接BE，则下列结论：①ED⊥BC；②∠A=∠EBA；③EB平分∠AED；④ED=AB中，正确的个数为（　　）
A．1个 B．2个 C．3个 D．4个
14．（2016?湖北校级模拟）如图，一块余料ABCD，AD∥BC，现进行如下操作：以点B为圆心，适当长为半径画弧，分别交BA，BC于点G，H；再分别以点G，H为圆心，大于GH的长为半径画弧，两弧在∠ABC内部相交于点O，画射线BO，交AD于点E．若∠A=100°，则∠EBC度数为（　　）
A．50° B．40° C．30° D．80°
　
二．解答题（共12小题）
15．（2016春?淄博期中）已知：∠α，∠β，线段c．
求作：△ABC，使∠A=α，∠B=∠β，AB=c
（不写作法，保留作图痕迹）
16．（2016?孝感）如图，在Rt△ABC中，∠ACB=90°．
（1）请用直尺和圆规按下列步骤作图，保留作图痕迹：
①作∠ACB的平分线，交斜边AB于点D；
②过点D作AC的垂线，垂足为点E．
（2）在（1）作出的图形中，若CB=4，CA=6，则DE=　　　　．
17．（2016?江西）如图，六个完全相同的小长方形拼成了一个大长方形，AB是其中一个小长方形的对角线，请在大长方形中完成下列画图，要求：①仅用无刻度直尺，②保留必要的画图痕迹．
（1）在图1中画出一个45°角，使点A或点B是这个角的顶点，且AB为这个角的一边；
（2）在图2中画出线段AB的垂直平分线．
18．（2016?大悟县二模）如图，已知在△ABC中，AB=AC．
（1）试用直尺和圆规在AC上找一点D，使AD=BD（不写作法，但需保留作图痕迹）．
（2）在（1）中，连接BD，若BD=BC，求∠A的度数．
19．（2016?孝南区一模）（1）如图，试用直尺与圆规在平面内确定一点O，使得点O到Rt△ABC的两边AC、BC的距离相等，并且点O到A、B两点的距离也相等．（不写作法，但需保留作图痕迹）2-1-c-n-j-y
（2）在（1）中，作OM⊥AC于M，ON⊥BC于N，连结AO、BO．求证：△OMA≌△ONB．
20．（2016?广州）如图，利用尺规，在△ABC的边AC上方作∠CAE=∠ACB，在射线AE上截取AD=BC，连接CD，并证明：CD∥AB（尺规作图要求保留作图痕迹，不写作法）
21．（2015?黄岛区校级模拟）用圆规、直尺作图，不写作法，但要保留作图痕迹．
如图，“幸福”小区为了方便住在A区、B区、和C区的居民（A区、B区、和C区之间均有小路连接），要在小区内设立物业管理处P．如果想使这个物业管理处P到A区、B区、和C区的距离相等，应将它建在什么位置？请在图中作出点P．
22．（2016?陕西校级模拟）某地拟在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉P到广场的两个入口A、B的距离相等，且到广场管理处C的距离等于A和B之间距离的一半，A、B、C的位置如图所示．请利用尺规作图作出音乐喷泉P的位置．（要求：不写作法，但要保留作图痕迹，必须用铅笔作图）．
23．（2016?颍泉区一模）如图，一个3×2的矩形（即长为3，宽为2）可以用两种不同方式分割成3或6个边长是正整数的小正方形，即：小正方形的个数最多是6个，最少是3个．
（1）一个5×2的矩形用不同的方式分割后，小正方形的个数可以是　　　　个，最少是　　　　个；
（2）一个7×2的矩形用不同的方式分割后，小正方形的个数最多是　　　　个，最少是　　　　个；
（3）一个（2n+1）×2的矩形用不同的方式分割后，小正方形的个数最多是　　　　个；最少是　　　　个．（n是正整数）
24．（2015?东城区二模）如果一条直线能够将一个封闭图形的周长和面积同时平分，那么就把这条直线称作这个封闭图形的二分线．
（1）请在图1的三个图形中，分别作一条二分线．
（2）请你在图2中用尺规作图法作一条直线 l，使得它既是矩形的二分线，又是圆的二分线．（保留作图痕迹，不写画法）．
（3）如图3，在Rt△ABC中，∠A=90°，AB=3，AC=4，是否存在过AB边上的点P的二分线？若存在，求出AP的长；若不存在，请说明理由．
　
25．（2013?青岛）已知：如图，直线AB与直线BC相交于点B，点D是直线BC上一点．
求作：点E，使直线DE∥AB，且点E到B，D两点的距离相等．（在题目的原图中完成作图）
结论：BE=DE．
26．（2015?枣庄模拟）如图（1），凸四边形ABCD，如果点P满足∠APD=∠APB=α，且∠BPC=∠CPD=β，则称点P为四边形ABCD的一个半等角点．
（1）在图（2）正方形ABCD内画一个半等角点P，且满足α≠β；
（2）在图（3）四边形ABCD中画出一个半等角点P，保留画图痕迹（不需写出画法）．
　

1.6尺规作图同步练习
参考答案与试题解析
　
一．选择题（共14小题）
1．（2016?曲靖）如图，C，E是直线l两侧的点，以C为圆心，CE长为半径画弧交l于A，B两点，又分别以A，B为圆心，大于AB的长为半径画弧，两弧交于点D，连接CA，CB，CD，下列结论不一定正确的是（　　）
A．CD⊥l B．点A，B关于直线CD对称
C．点C，D关于直线l对称 D．CD平分∠ACB
【解答】解：由作法得CD垂直平分AB，所以A、B选项正确；
因为CD垂直平分AB，
所以CA=CB，
所以CD平分∠ACB，所以D选项正确；
因为AD不一定等于AD，所以C选项错误．
故选C．
　
2．（2016?锦州）如图，在△ABC中，∠C=90°，分别以点A、B为圆心，大于AB长为半径作弧，两弧分别交于M、N两点，过M、N两点的直线交AC于点E，若AC=6，BC=3，则CE的长为（　　）
A． B． C． D．
【解答】解：∵∠C=90°，
∴∠A+∠CBA=90°，
由作图可得MN是AB的垂直平分线，
∴AE=EB=6﹣CE，
∴CE2+BC2=BE2，
即CE2+32=（6﹣CE）2，
∴CE=，
故选A．
　
3．（2016?漳州）下列尺规作图，能判断AD是△ABC边上的高是（　　）
A． B． C． D．
【解答】解：过点A作BC的垂线，垂足为D，
故选B．
　
4．（2016?河北）如图，已知钝角△ABC，依下列步骤尺规作图，并保留作图痕迹．
步骤1：以C为圆心，CA为半径画弧①；
步骤2：以B为圆心，BA为半径画弧②，交弧①于点D；
步骤3：连接AD，交BC延长线于点H．
下列叙述正确的是（　　）
A．BH垂直平分线段AD B．AC平分∠BAD
C．S△ABC=BC?AH D．AB=AD
【解答】解：A、正确．如图连接CD、BD，
∵CA=CD，BA=BD，
∴点C、点B在线段AD的垂直平分线上，
∴直线BC是线段AD的垂直平分线，
故A正确．
B、错误．CA不一定平分∠BDA．
C、错误．应该是S△ABC=?BC?AH．
D、错误．根据条件AB不一定等于AD．
故选A．
　
5．（2016?丽水）用直尺和圆规作Rt△ABC斜边AB上的高线CD，以下四个作图中，作法错误的是（　　）21·cn·jy·com
A． B． C． D．
【解答】解：A、根据垂径定理作图的方法可知，CD是Rt△ABC斜边AB上的高线，不符合题意；
B、根据直径所对的圆周角是直角的方法可知，CD是Rt△ABC斜边AB上的高线，不符合题意；
C、根据相交两圆的公共弦的性质可知，CD是Rt△ABC斜边AB上的高线，不符合题意；
D、无法证明CD是Rt△ABC斜边AB上的高线，符合题意．
故选：D．
　
6．（2016?台湾）如图，△ABC中，∠A=60°，∠B=58°．甲、乙两人想在△ABC外部取一点D，使得△ABC与△DCB全等，其作法如下：21世纪教育网版权所有
（甲） 1．作∠A的角平分线L．
2．以B为圆心，BC长为半径画弧，交L于D点，则D即为所求．
（乙） 1．过B作平行AC的直线L．
2．过C作平行AB的直线M，交L于D点，则D即为所求．
对于甲、乙两人的作法，下列判断何者正确？（　　）
A．两人皆正确 B．两人皆错误
C．甲正确，乙错误 D．甲错误，乙正确
【解答】解：（甲）如图一所示，
∵∠A=60°，∠B=58°，
∴∠ACB=62°，
∴AB≠BC≠CA，
由甲的作法可知，BC=BD，
故△ABC和△DCB不可能全等，
故甲的作法错误；
（乙）如图二所示，
∵BD∥AC，CD∥AB，
∴∠ABC=DCB，∠ACB=∠DBC，
在△ABC和△DCB中，
∴△ABC≌△DCB（ASA），
∴乙的作法是正确的．
故选D．
　
7．（2016?阳泉模拟）下列关于尺规的功能说法不正确的是（　　）
A．直尺的功能是：在两点间连接一条线段，将线段向两方向延长
B．直尺的功能是：可作平角和直角
C．圆规的功能是：以任意长为半径，以任意点为圆心作一个圆
D．圆规的功能是：以任意长为半径，以任意点为圆心作一段弧
【解答】解：A、直尺的功能是：在两点间连接一条线段，将线段向两方向延长．正确．
B、直尺的功能是：可作平角和直角．错误．
C、圆规的功能是：以任意长为半径，以任意点为圆心作一个圆．正确．
D、圆规的功能是：以任意长为半径，以任意点为圆心作一段弧．正确．
故选B
　
8．（2016?开平区一模）如图，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，分别交AB、AC于E、F两点；再分别以E、F为圆心，大于EF长为半径作圆弧，两条圆弧交于点G，作射线AG交CD于点H．若∠C=140°，则∠AHC的大小是（　　）
A．20° B．25° C．30° D．40°
【解答】解：由题意可得：AH平分∠CAB，
∵AB∥CD，
∴∠C+∠CAB=180°，
∵∠ACD=140°，
∴∠CAB=40°，
∵AH平分∠CAB，
∴∠HAB=20°，
∴∠AHC=20°．
故选A．
　
9．（2016?柘城县一模）如图，已知△ABC，∠C=90°，按以下步骤：①分别以A、B为圆心，以大于的长为半径作弧，两弧相交于两点M、N；②作直线MN交BC于点D．若AC=1.5，∠B=15°．则BD等于（　　）www.21-cn-jy.com
A．1.5 B．2 C．2.5 D．3
【解答】解：由作法得MN垂直平分AB，连结AD，如图，则DB=DA，
∴∠B=∠DAB=15°，
∴∠ADC=∠B+∠DAB=30°，
在Rt△ADC中，AD=2AC=2×1.5=3．
∴BD=DA=3．
故选D．
　
10．（2016?商丘模拟）如图，在△ABC中，AD平分∠BAC，按如下步骤作图：①分别以点A、D为圆心，以大于AD的长为半径在AD两侧作弧，交于两点M、N；②连接MN分别交AB、AC于点E、F；③连接DE、DF．若BD=6，AF=4，CD=3，则BE的长是（　　）
A．2 B．4 C．6 D．8
【解答】解：∵根据作法可知：MN是线段AD的垂直平分线，
∴AE=DE，AF=DF，
∴∠EAD=∠EDA，
∵AD平分∠BAC，
∴∠BAD=∠CAD，
∴∠EDA=∠CAD，
∴DE∥AC，
同理DF∥AE，
∴四边形AEDF是菱形，
∴AE=DE=DF=AF，
∵AF=4，
∴AE=DE=DF=AF=4，
∵DE∥AC，
∴=，
∵BD=6，AE=4，CD=3，
∴=，
∴BE=8，
故选D．
　
11．（2016?东台市二模）如图，利用尺规作的角平分线OC，在用尺规作角平分线时，用到的三角形全等的判定方法是（　　）21cnjy.com
作法：①以O为圆心，任意长为半径作弧，交OA，OB于点D，E．
②分别以D，E为圆心，以大于DE的长为半径作弧，两弧在∠AOB内交于点C．
③作射线OC．则OC就是∠AOB的平分线．
A．SSS B．SAS C．ASA D．AAS
【解答】解：由作法得OE=OD，CE=CD，
而OC为公共边，
所以可根据“SSS”证明△COD≌△COE，
所以∠COD=∠COE，即OC平分∠AOB．
故选A．
　
12．（2016?温岭市一模）“过直线外一点作已知直线的垂线”．下列尺规作图中对应的正确作法是（　　）2·1·c·n·j·y
A． B． C． D．
【解答】解：A、是作角平分线，故本选项错误；
B、是作线段的垂直平分线，故本选项错误；
C、过直线外一点作已知直线的垂线，故本选项正确；
D、是作线段的垂直平分线，故本选项错误．
故选C．
　
13．（2016?许昌一模）如图，已知在Rt△ABC中，∠ABC=90°，点D是BC边的中点，分别以B、C为圆心，大于BC长为半径画弧，两弧在直线BC上方的交点为P，直线PD交AC于点E，连接BE，则下列结论：①ED⊥BC；②∠A=∠EBA；③EB平分∠AED；④ED=AB中，正确的个数为（　　）21·世纪*教育网
A．1个 B．2个 C．3个 D．4个
【解答】解：∵由作图可得P到B、C两点距离相等，
又∵点D是BC边的中点，
∴PD是BC的垂直平分线，故①正确；
∵PD是BC的垂直平分线，
∴EB=EC，
∴∠C=∠EBC，
∵∠ABC=90°，
∴∠A+∠C=90°，∠ABE+∠EBC=90°，
∴∠A=∠EBA，故②正确；
根据所给条件无法证明EB平分∠AED，故③错误；
∵∠A=∠EBA，
∴AE=BE，
∵BE=EC，
∴EA=EC，
∵D为BC中点，
∴DE是△ABC的中位线，
∴ED=AB，故④正确；
正确的共有3个，
故选：C．
　
14．（2016?湖北校级模拟）如图，一块余料ABCD，AD∥BC，现进行如下操作：以点B为圆心，适当长为半径画弧，分别交BA，BC于点G，H；再分别以点G，H为圆心，大于GH的长为半径画弧，两弧在∠ABC内部相交于点O，画射线BO，交AD于点E．若∠A=100°，则∠EBC度数为（　　）【来源：21·世纪·教育·网】
A．50° B．40° C．30° D．80°
【解答】解：∵AD∥BC，
∴∠AEB=∠EBC．
由BE是∠ABC的角平分线，
∴∠EBC=∠ABE，
∴∠AEB=∠ABE，
由∠A=100°，得
∠ABE=∠AEB=40°．
由AD∥BC，得
∠EBC=∠AEB=40°．
故选B．
　
15．（2016春?淄博期中）已知：∠α，∠β，线段c．
求作：△ABC，使∠A=α，∠B=∠β，AB=c
（不写作法，保留作图痕迹）
【解答】解：如图所示：△ABC即为所求．
　
16．（2016?孝感）如图，在Rt△ABC中，∠ACB=90°．
（1）请用直尺和圆规按下列步骤作图，保留作图痕迹：
①作∠ACB的平分线，交斜边AB于点D；
②过点D作AC的垂线，垂足为点E．
（2）在（1）作出的图形中，若CB=4，CA=6，则DE=　　．
【解答】解：（1）如图所示；
（2）解：∵DC是∠ACB的平分线，
∴∠BCD=∠ACD，
∵DE⊥AC，BC⊥AC，
∴DE∥BC，∴∠EDC=∠BCD，
∴∠ECD=∠EDC，∴DE=CE，
∵DE∥BC，
∴△ADE∽△ABC，
∴=，
设DE=CE=x，则AE=6﹣x，
∴=，
解得：x=，
即DE=，
故答案为：．
　
17．（2016?江西）如图，六个完全相同的小长方形拼成了一个大长方形，AB是其中一个小长方形的对角线，请在大长方形中完成下列画图，要求：①仅用无刻度直尺，②保留必要的画图痕迹．21教育网
（1）在图1中画出一个45°角，使点A或点B是这个角的顶点，且AB为这个角的一边；
（2）在图2中画出线段AB的垂直平分线．
【解答】解：（1）如图所示，∠ABC=45°．（AB、AC是小长方形的对角线）．
（2）线段AB的垂直平分线如图所示，
点M是长方形AFBE是对角线交点，点N是正方形ABCD的对角线的交点，直线MN就是所求的线段AB的垂直平分线．www-2-1-cnjy-com
　
18．（2016?大悟县二模）如图，已知在△ABC中，AB=AC．
（1）试用直尺和圆规在AC上找一点D，使AD=BD（不写作法，但需保留作图痕迹）．
（2）在（1）中，连接BD，若BD=BC，求∠A的度数．
【解答】解：（1）如图所示：
（2）设∠A=x，
∵AD=BD，
∴∠DBA=∠A=x，
在△ABD中
∠BDC=∠A+∠DBA=2x，
又∵BD=BC，
∴∠C=∠BDC=2x，
又∵AB=AC，
∴∠ABC=∠C=2x，
在△ABC中
∠A+∠ABC+∠C=180°，
∴x+2x+2x=180°，
∴x=36°．
　
19．（2016?孝南区一模）（1）如图，试用直尺与圆规在平面内确定一点O，使得点O到Rt△ABC的两边AC、BC的距离相等，并且点O到A、B两点的距离也相等．（不写作法，但需保留作图痕迹）　　21*cnjy*com
（2）在（1）中，作OM⊥AC于M，ON⊥BC于N，连结AO、BO．求证：△OMA≌△ONB．
【解答】解：（1）如图1，
（2）如图2，
∵OC平分∠ACB，OM⊥AC，ON⊥CN，
∴OM=ON，
∵点O在线段AB的垂直平分线上，
∴OA=OB，
在Rt△△OMA和△ONB中，
，
∴△OMA≌△ONB．
　
20．（2016?广州）如图，利用尺规，在△ABC的边AC上方作∠CAE=∠ACB，在射线AE上截取AD=BC，连接CD，并证明：CD∥AB（尺规作图要求保留作图痕迹，不写作法）
【解答】解：图象如图所示，
∵∠EAC=∠ACB，
∴AD∥CB，
∵AD=BC，
∴四边形ABCD是平行四边形，
∴AB∥CD．
　
21．（2015?黄岛区校级模拟）用圆规、直尺作图，不写作法，但要保留作图痕迹．
如图，“幸福”小区为了方便住在A区、B区、和C区的居民（A区、B区、和C区之间均有小路连接），要在小区内设立物业管理处P．如果想使这个物业管理处P到A区、B区、和C区的距离相等，应将它建在什么位置？请在图中作出点P．【来源：21cnj*y.co*m】
【解答】解：如图所示：
．
　
22．（2016?陕西校级模拟）某地拟在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉P到广场的两个入口A、B的距离相等，且到广场管理处C的距离等于A和B之间距离的一半，A、B、C的位置如图所示．请利用尺规作图作出音乐喷泉P的位置．（要求：不写作法，但要保留作图痕迹，必须用铅笔作图）．【出处：21教育名师】
【解答】解：如图，
　
23．（2016?颍泉区一模）如图，一个3×2的矩形（即长为3，宽为2）可以用两种不同方式分割成3或6个边长是正整数的小正方形，即：小正方形的个数最多是6个，最少是3个．
（1）一个5×2的矩形用不同的方式分割后，小正方形的个数可以是　10　个，最少是　4　个；
（2）一个7×2的矩形用不同的方式分割后，小正方形的个数最多是　14　个，最少是　5　个；
（3）一个（2n+1）×2的矩形用不同的方式分割后，小正方形的个数最多是　4n+2　个；最少是　n+2　个．（n是正整数）【版权所有：21教育】
【解答】解：（1）一个5×2的矩形最少可分成4个正方形，最多可分成10个正方形；
（2）一个7×2的矩形最少可分成5个正方形，最多可分成14个正方形；
（3）第一个图形：是一个3×2的矩形，最少可分成1+2个正方形，最多可分成1×4+2个正方形；
第二个图形：是一个5×2的矩形，最少可分成2+2个正方形，最多可分成2×4+2个正方形；
第三个图形：是一个7×2的矩形，最少可分成3+2个正方形，最多可分成3×4+2个正方形；
…
第n个图形：是一个（2n+1）×2的矩形，最多可分成n×4+2=4n+2个正方形，最少可分成n+2个正方形．21教育名师原创作品
故答案为：（1）10；4；（2）14；5；（3）4n+2；n+2．
　
24．（2015?东城区二模）如果一条直线能够将一个封闭图形的周长和面积同时平分，那么就把这条直线称作这个封闭图形的二分线．21*cnjy*com
（1）请在图1的三个图形中，分别作一条二分线．
（2）请你在图2中用尺规作图法作一条直线 l，使得它既是矩形的二分线，又是圆的二分线．（保留作图痕迹，不写画法）．
（3）如图3，在Rt△ABC中，∠A=90°，AB=3，AC=4，是否存在过AB边上的点P的二分线？若存在，求出AP的长；若不存在，请说明理由．
【解答】解：（1）（2）如图所示：
．
（3）存在，
理由：设AP=x，PQ为二分线，则Q在BC边上，CQ=2﹣x，BQ=x+3，BP=3﹣x，
过点Q做QE⊥AB于E，
则QE=，
∵S△PBQ=3，
∴（3﹣x）?=3，
∴x=．
∴AP=．
　
25．（2013?青岛）已知：如图，直线AB与直线BC相交于点B，点D是直线BC上一点．
求作：点E，使直线DE∥AB，且点E到B，D两点的距离相等．（在题目的原图中完成作图）
结论：BE=DE．
【解答】解：如图所示：
点E即为所求，BE=DE
　
26．（2015?枣庄模拟）如图（1），凸四边形ABCD，如果点P满足∠APD=∠APB=α，且∠BPC=∠CPD=β，则称点P为四边形ABCD的一个半等角点．
（1）在图（2）正方形ABCD内画一个半等角点P，且满足α≠β；
（2）在图（3）四边形ABCD中画出一个半等角点P，保留画图痕迹（不需写出画法）．
【解答】解：
（1）所画的点P在AC上且不是AC的中点和AC的端点．
（如图（2））
（2）画点B关于AC的对称点B′，延长DB′交AC于点P，点P为所求（不写文字说明不扣分）．
（说明：画出的点P大约是四边形ABCD的半等角点，而无对称的画图痕迹，给1分）