1.5三角形全等的判定(AAS)同步练习
文档属性
| 名称 | 1.5三角形全等的判定(AAS)同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 349.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-12 07:45:04 | ||
图片预览



文档简介
1.5三角形全等的判断(AAS)
一.选择题(共15小题)
1.(2016春?成安县期末)在△ABC和△AˊB′C′中,已知∠A=∠A′,AB=A′B′,在下面判断中错误的是( )
A.若添加条件AC=A′C′,则△ABC≌△A′B′C′
B.若添加条件BC=B′C′,则△ABC≌△A′B′C′
C.若添加条件∠B=∠B′,则△ABC≌△A′B′C′
D.若添加条件∠C=∠C′,则△ABC≌△A′B′C′
2.如图,AB与CD相交于点E,AD=CB,若使△AED≌△CEB,则应补充的条件是( )
A.∠A=∠C B.AE=CE C.DE=BE D.不用补充条件
3.(2016?金华)如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )21cnjy.com
A.AC=BD B.∠CAB=∠DBA C.∠C=∠D D.BC=AD
4.(2015春?禅城区校级期末)下列条件中能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D B.∠A=∠D,∠B=∠E,∠C=∠F
C.AC=DF,∠B=∠F,AB=DE D.∠B=∠E,∠C=∠F,AC=DF
5.(2016春?毕节市校级期中)下列判断中错误的是( )
A.有两角和一边对应相等的两个三角形全等
B.有一边对应相等的两个等边三角形全等
C.有两边和其中一边上的中线对应相等的两个三角形全等
D.有两边和一角对应相等的两个三角形全等
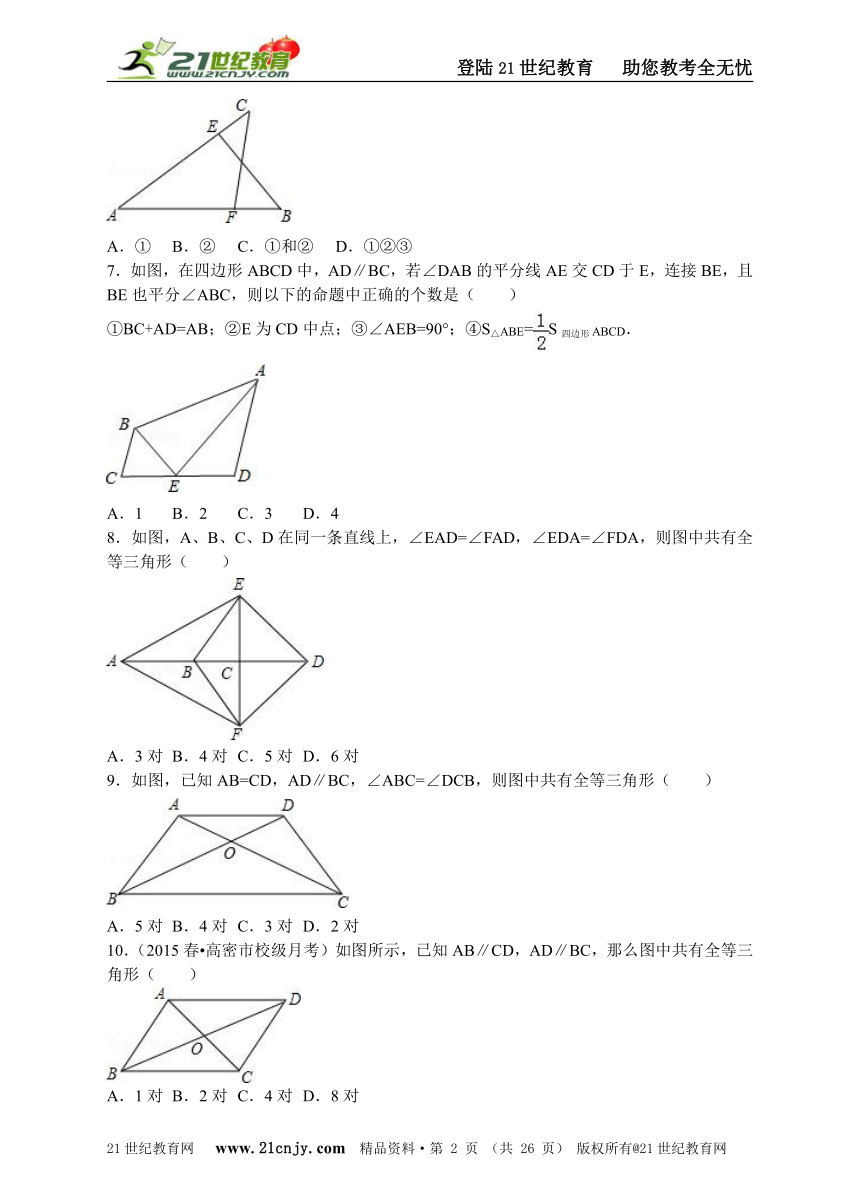
6.(2016?武城县一模)如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )
A.① B.② C.①和② D.①②③
7.如图,在四边形ABCD中,AD∥BC,若∠DAB的平分线AE交CD于E,连接BE,且BE也平分∠ABC,则以下的命题中正确的个数是( )
①BC+AD=AB;②E为CD中点;③∠AEB=90°;④S△ABE=S四边形ABCD.
A.1 B.2 C.3 D.4
8.如图,A、B、C、D在同一条直线上,∠EAD=∠FAD,∠EDA=∠FDA,则图中共有全等三角形( )【版权所有:21教育】
A.3对 B.4对 C.5对 D.6对
9.如图,已知AB=CD,AD∥BC,∠ABC=∠DCB,则图中共有全等三角形( )
A.5对 B.4对 C.3对 D.2对
10.(2015春?高密市校级月考)如图所示,已知AB∥CD,AD∥BC,那么图中共有全等三角形( )21·世纪*教育网
A.1对 B.2对 C.4对 D.8对
11.(2015秋?南开区期末)在△ABC和△A′B′C′中,已知∠A=∠A′,AB=A′B′,添加下列条件中的一个,不能使△ABC≌△A′B′C′一定成立的是( )
A.AC=A′C′ B.BC=B′C′ C.∠B=∠B′ D.∠C=∠C′
12.(2015秋?蜀山区期末)如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )
A.AB=DE B.DF∥AC C.∠E=∠ABC D.AB∥DE
13.(2015?新泰市二模)如图所示,∠E=∠F,∠B=∠C,AE=AF,以下结论:①∠FAN=∠EAM;②EM=FN;③△ACN≌△ABM;④CD=DN.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
14.(2016?济南校级一模)如图,在△ABC与△DEF中,已有条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是( )
A.∠B=∠E,BC=EF B.BC=EF,AC=DF C.∠A=∠D,∠B=∠E D.∠A=∠D,BC=EF
15.(2016?黔西南州)如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE B.AC=DF C.∠A=∠D D.BF=EC
三.解答题(共13小题)
16.如图,已知:点B、E、F、C在同一直线上,∠A=∠D,BE=CF,且AB∥CD.求证:AF∥EDwww.21-cn-jy.com
证明:∵BE=FC
∴BE+EF=FC+EF( )
即:
∵AB∥CD
∴∠B=∠C( )
∠A=∠D
∠B=∠C
在△ABF和△DCE中,有
BF=CE
∴△ABF≌△DCE( )
∴∠AFB=∠DEC( )
∴AF∥ED( )
17.已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F,求证: 21*cnjy*com
(1)AC=2BF;
(2)AB垂直平分DF.
18.如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,D、E为垂足.求证:DE+BE=CE.
19.已知:如图,在Rt△ABC中,∠ACB=90°,∠B=60°,AD,CE是角平分线,AD与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为M,N.求证:FE=FD.
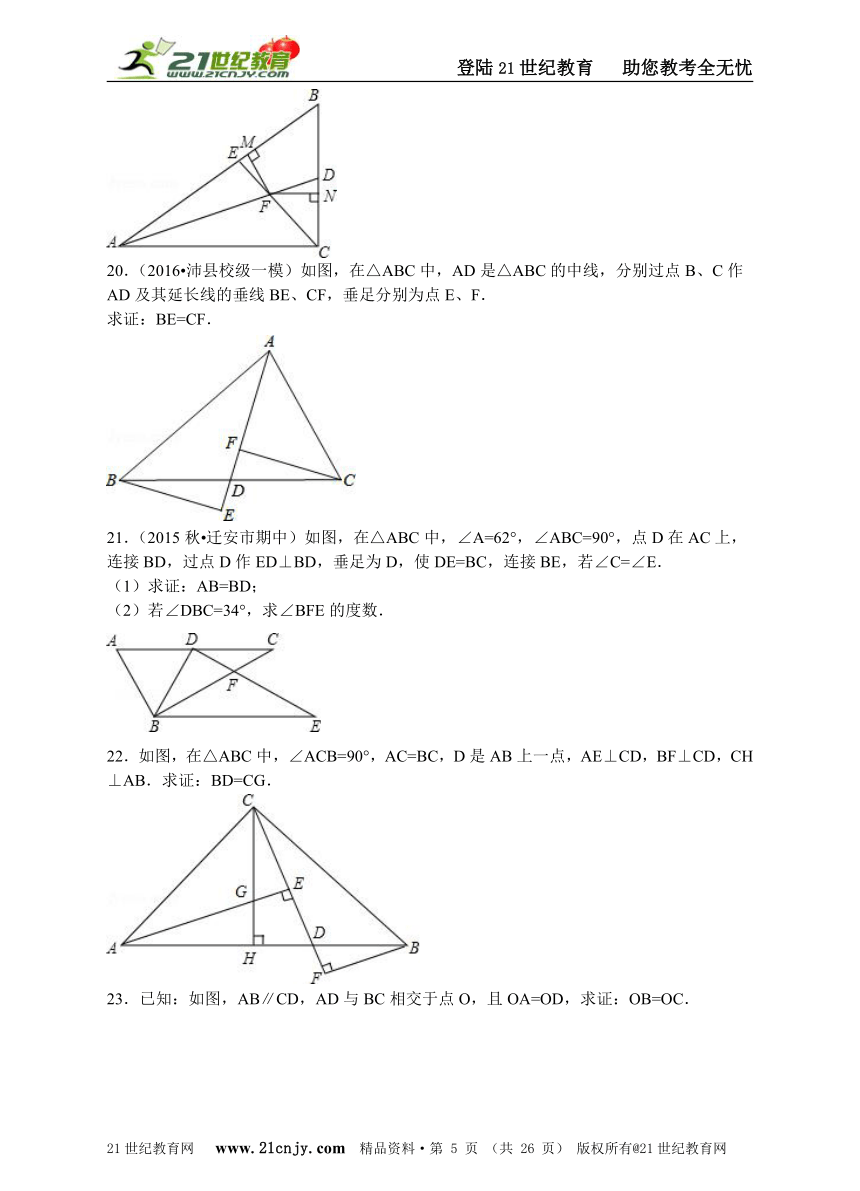
20.(2016?沛县校级一模)如图,在△ABC中,AD是△ABC的中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.
求证:BE=CF.
21.(2015秋?迁安市期中)如图,在△ABC中,∠A=62°,∠ABC=90°,点D在AC上,连接BD,过点D作ED⊥BD,垂足为D,使DE=BC,连接BE,若∠C=∠E.
(1)求证:AB=BD;
(2)若∠DBC=34°,求∠BFE的度数.
22.如图,在△ABC中,∠ACB=90°,AC=BC,D是AB上一点,AE⊥CD,BF⊥CD,CH⊥AB.求证:BD=CG.
23.已知:如图,AB∥CD,AD与BC相交于点O,且OA=OD,求证:OB=OC.
24.(2015秋?奉贤区期中)如图,已知在△ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE.
(1)求证:DE∥BC;
(2)如果F是BC延长线上一点,且∠EBC=∠EFC,求证:DE=CF.
25.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)如图①,BF垂直CE于点F,交CD于点G,试说明AE=CG;
(2)如图②,作AH垂直于CE的延长线,垂足为H,交CD的延长线于点M,则图中与BE相等的线段是 ,并说明理由.
26.已知:如图,在△ABC中,∠BAC=90°,AB=AC,l是过点A的一条直线,BD⊥l,CE⊥l,垂足分别为D、E.
(1)如图①,求证:DE=BD+CE;
(2)若直线l绕A点旋转到图②位置时,其余条件不变,请把图形补充完整,写出BD、CE与DE之间的数量关系,并证明你的结论.
27.如图,点D,E分别是ABC的边BC,AC上的点,BE,AD交于F,已知AB=AC,∠BAC=∠AFE=2∠ACB=2α,G为AC上的点,∠AEB=∠CGD.探究线段AE,GC的数量关系,并说明理由.
1.5三角形全等的判断(AAS)
参考答案与试题解析
一.选择题(共15小题)
1.(2016春?成安县期末)在△ABC和△AˊB′C′中,已知∠A=∠A′,AB=A′B′,在下面判断中错误的是( )
A.若添加条件AC=A′C′,则△ABC≌△A′B′C′
B.若添加条件BC=B′C′,则△ABC≌△A′B′C′
C.若添加条件∠B=∠B′,则△ABC≌△A′B′C′
D.若添加条件∠C=∠C′,则△ABC≌△A′B′C′
【解答】解:A,正确,符合SAS判定;
B,不正确,因为边BC与B′C′不是∠A与∠A′的一边,所以不能推出两三角形全等;
C,正确,符合AAS判定;
D,正确,符合ASA判定;
故选B.
2.如图,AB与CD相交于点E,AD=CB,若使△AED≌△CEB,则应补充的条件是( )
A.∠A=∠C B.AE=CE C.DE=BE D.不用补充条件
【解答】解:∵AD=CB,
而∠AED=∠BEC,
∴当∠A=∠C时,可判断△AED≌△CEB.
故选A.
3.(2016?金华)如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
A.AC=BD B.∠CAB=∠DBA C.∠C=∠D D.BC=AD
【解答】解:由题意,得∠ABC=∠BAD,AB=BA,
A、∠ABC=∠BAD,AB=BA,AC=BD,(SSA)三角形不全等,故A错误;
B、在△ABC与△BAD中,,△ABC≌△BAD(ASA),故B正确;
C、在△ABC与△BAD中,,△ABC≌△BAD(AAS),故C正确;
D、在△ABC与△BAD中,,△ABC≌△BAD(SAS),故D正确;
故选:A.
4.(2015春?禅城区校级期末)下列条件中能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D B.∠A=∠D,∠B=∠E,∠C=∠F
C.AC=DF,∠B=∠F,AB=DE D.∠B=∠E,∠C=∠F,AC=DF
【解答】解:
A、根据AB=DE,BC=EF,∠A=∠D,不能判断△ABC≌△DEF,故本选项错误;
B、根据∠A=∠D,∠B=∠E,∠C=∠F,不能判断△ABC≌△DEF,故本选项错误;
C、根据AC=DF,∠B=∠F,AB=DE,不能判断△ABC≌△DEF,故本选项错误;
D、∵在△ABC和△DEF中
,
∴△ABC≌△DEF(AAS),故本选项正确;
故选D.
5.(2016春?毕节市校级期中)下列判断中错误的是( )
A.有两角和一边对应相等的两个三角形全等
B.有一边对应相等的两个等边三角形全等
C.有两边和其中一边上的中线对应相等的两个三角形全等
D.有两边和一角对应相等的两个三角形全等
【解答】解:A、有两角和一边对应相等的两个三角形全等,说法正确;
B、有一边对应相等的两个等边三角形全等,说法正确;
C、有两边和其中一边上的中线对应相等的两个三角形全等,说法正确;
D、有两边和一角对应相等的两个三角形全等,说法错误;
故选:D.
6.(2016?武城县一模)如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )【来源:21cnj*y.co*m】
A.① B.② C.①和② D.①②③
【解答】解:如图,连接AD;
在△ABE与△ACF中,
,
∴△ABE≌△ACF(SAS);
∴∠B=∠C;
∵AB=AC,AE=AF,
∴BF=CE;
在△CDE与△BDF中,
,
∴△CDE≌△BDF(AAS),
∴DC=DB;
在△ADC与△ADB中,
,
∴△ADC≌△ADB(SAS),
∴∠CAD=∠BAD;
综上所述,①②③均正确,
故选D
7.如图,在四边形ABCD中,AD∥BC,若∠DAB的平分线AE交CD于E,连接BE,且BE也平分∠ABC,则以下的命题中正确的个数是( )【来源:21·世纪·教育·网】
①BC+AD=AB;②E为CD中点;③∠AEB=90°;④S△ABE=S四边形ABCD.
A.1 B.2 C.3 D.4
【解答】解:在AB上截取AF=AD.
则△AED≌△AEF(SAS).
∴∠AFE=∠D.
∵AD∥BC,∴∠D+∠C=180°.
∴∠C=∠BFE.
∴△BEC≌△BEF(AAS).
∴①BC=BF,故AB=BC+AD;
②CE=EF=ED,即E是CD中点;
③∠AEB=∠AEF+∠BEF=∠DEF+∠CEF=×180°=90°;
④S△AEF=S△AED,S△BEF=S△BEC,
∴S△AEB=S四边形BCEF+S四边形EFAD=S四边形ABCD.
故选D.
8.如图,A、B、C、D在同一条直线上,∠EAD=∠FAD,∠EDA=∠FDA,则图中共有全等三角形( )www-2-1-cnjy-com
A.3对 B.4对 C.5对 D.6对
【解答】解析:在△ADE与△ADF中,
,
∴△ADE≌△ADF(ASA);
∴AE=AF,DE=DF;
同理可证:△ABE≌ABF;△ACE≌△ACF;△DCE≌△DCF;△BCE≌△BCF;△BDE≌△BDF,综上所述,图中共有全等三角形6对,2-1-c-n-j-y
故选D.
9.如图,已知AB=CD,AD∥BC,∠ABC=∠DCB,则图中共有全等三角形( )
A.5对 B.4对 C.3对 D.2对
【解答】解:在△ABC和△DCB中,
,
∴△ABC≌△DCB(SAS),
∴∠ACB=∠DBC,AC=BD,
∵AD∥BC,
∴∠ADB=∠DBC,∠DAC=∠ACB,
∴∠DAC=∠ADB,
在△ADC和△DAB中,
,
∴△ADC≌△DAB(SAS),
∴∠ABD=∠DCA,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(AAS),
故选:C.
10.(2015春?高密市校级月考)如图所示,已知AB∥CD,AD∥BC,那么图中共有全等三角形( )【出处:21教育名师】
A.1对 B.2对 C.4对 D.8对
【解答】解:全等三角形有△ABD≌△CDB,△ACD≌△CAB,△AOD≌△COB,△AOB≌△COD,共4对,
故选C.
11.(2015秋?南开区期末)在△ABC和△A′B′C′中,已知∠A=∠A′,AB=A′B′,添加下列条件中的一个,不能使△ABC≌△A′B′C′一定成立的是( )
A.AC=A′C′ B.BC=B′C′ C.∠B=∠B′ D.∠C=∠C′
【解答】解:
A、∠A=∠A′,AB=A′B′AC=A′C′,根据SAS能推出△ABC≌△A′B′C′,故A选项错误;
B、具备∠A=∠A′,AB=A′B′,BC=B′C′,不能判断△ABC≌△A′B′C′,故B选项正确;
C、根据ASA能推出△ABC≌△A′B′C′,故C选项错误;
D、根据AAS能推出△ABC≌△A′B′C′,故D选项错误.
故选:B.
12.(2015秋?蜀山区期末)如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )
A.AB=DE B.DF∥AC C.∠E=∠ABC D.AB∥DE
【解答】解:A、添加DE=AB与原条件满足SSA,不能证明△ABC≌△DEF,故A选项正确.
B、添加DF∥AC,可得∠DFE=∠ACB,根据AAS能证明△ABC≌△DEF,故B选项错误.
C、添加∠E=∠ABC,根据AAS能证明△ABC≌△DEF,故C选项错误.
D、添加AB∥DE,可得∠E=∠ABC,根据AAS能证明△ABC≌△DEF,故D选项错误.
故选:A.
13.(2015?新泰市二模)如图所示,∠E=∠F,∠B=∠C,AE=AF,以下结论:①∠FAN=∠EAM;②EM=FN;③△ACN≌△ABM;④CD=DN.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:在△ABE和△ACF中,
,
∴△ABE≌△ACF(AAS),
∴∠BAE=∠CAF,
∴∠FAN=∠EAM,
∴①正确;
在△AEM和△AFN中,
,
∴△AEM≌△AFN(ASA),
∴EM=FN,AM=AN,
∴②正确;
在△ACN和△ABM中,
,
∴△ACN≌△ABM(AAS),
∴③正确,
④不正确;
正确的结论有3个.
故选:C.
14.(2016?济南校级一模)如图,在△ABC与△DEF中,已有条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是( )21教育名师原创作品
A.∠B=∠E,BC=EF B.BC=EF,AC=DF C.∠A=∠D,∠B=∠E D.∠A=∠D,BC=EF
【解答】解:(1)在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS);故A正确;
(2)在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS);故B正确;
(3)在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA);故C正确;
(4)无法证明△ABC≌△DEF,故D错误;
故选 D.
15.(2016?黔西南州)如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE B.AC=DF C.∠A=∠D D.BF=EC
【解答】解:解:选项A、添加AB=DE可用AAS进行判定,故本选项错误;
选项B、添加AC=DF可用AAS进行判定,故本选项错误;
选项C、添加∠A=∠D不能判定△ABC≌△DEF,故本选项正确;
选项D、添加BF=EC可得出BC=EF,然后可用ASA进行判定,故本选项错误.
故选C.
三.解答题(共13小题)
16.如图,已知:点B、E、F、C在同一直线上,∠A=∠D,BE=CF,且AB∥CD.求证:AF∥ED
证明:∵BE=FC
∴BE+EF=FC+EF( 等式的性质 )
即: BF=CE
∵AB∥CD
∴∠B=∠C( 两直线平行内错角相等 )
∠A=∠D
∠B=∠C
在△ABF和△DCE中,有
BF=CE
∴△ABF≌△DCE( AAS )
∴∠AFB=∠DEC( 全等三角形对应角相等 )
∴AF∥ED( 内错角相等两直线平行 )
【解答】证明:∵BE=FC,
∴BE+EF=FC+EF(等式的性质),
即BF=CE,
∵AB∥CD,
∴∠B=∠C(两直线平行内错角相等),
∠A=∠D,
∠B=∠C,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(AAS),
∴∠AFB=∠DEC(全等三角形对应角相等),
∴AF∥ED(内错角相等两直线平行).
故答案为:等式的性质;BF=CE;两直线平行内错角相等;AAS;全等三角形对应角相等;内错角相等两直线平行
17.已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F,求证:
(1)AC=2BF;
(2)AB垂直平分DF.
【解答】证明:(1)∵BF∥AC,
∴BC⊥BF,
∵∠DCE+∠F=90°,∠DCE+∠CDA=90°,
∴∠CDA=∠F,
在△ACD和△CBF中,
,
∴△ACD≌△CBF(AAS),
∴CD=BF,
∵点D是BC的中点,
∴AC=BC=2CD,
∴AC=2BF;
(2)连接DF交AB于G点,
∵点D是BC的中点,
∴AC=2BD,
∵AC=2BF,
∴BD=BF,
∵AC=BC,∠ACB=90°,
∴∠ABC=45°,
∵△ACD≌△CBF,
∴∠CBF=∠ACD=90°,
∴∠ABF=45°,
在△DBG和△FBG中,
,
∴△DBG≌△FBG(SAS),
∴DG=FG,∠DGB=∠FGB,
∵∠DGB+∠FGB=180°,
∴∠DGB=∠FGB=90°,
∴AB垂直平分DF.
18.如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,D、E为垂足.求证:DE+BE=CE.2·1·c·n·j·y
【解答】证明:∵∠ACB=90°,BE⊥CE,AD⊥CE,
∴∠BEC=∠ACB=∠ADC=90°,
∴∠ACE+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中
,
∴△ADC≌△CEB(AAS).
∴BE=CD,
∴CE=CD+DE=DE+BE.
19.已知:如图,在Rt△ABC中,∠ACB=90°,∠B=60°,AD,CE是角平分线,AD与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为M,N.求证:FE=FD.
【解答】证明:连接BF,
∵F是角平分线交点,
∴BF也是角平分线,
∴MF=FN,∠DNF=∠EMF=90°,
∵在Rt△ABC中,∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∴∠DAC=∠BAC=15°,
∴∠CDA=75°,
∵∠NFC=45°,∠MFN=120°,
∴∠MFE=15°,
∴∠MEF=75°=∠NDF,
在△DNF和△EMF中,
,
∴△DNF≌△EMF(AAS),
∴FE=FD.
20.(2016?沛县校级一模)如图,在△ABC中,AD是△ABC的中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.21*cnjy*com
求证:BE=CF.
【解答】解:∵BE⊥AE,CF⊥AE,
∴∠BED=∠CFD=90°,
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS),
∴BE=CF.
21.(2015秋?迁安市期中)如图,在△ABC中,∠A=62°,∠ABC=90°,点D在AC上,连接BD,过点D作ED⊥BD,垂足为D,使DE=BC,连接BE,若∠C=∠E.
(1)求证:AB=BD;
(2)若∠DBC=34°,求∠BFE的度数.
【解答】解:(1)∵∠ABC=90°,
∴∠A+∠C=90°,
∵ED⊥BD,
∴∠BDE=90°,
∵∠C=∠E,
∴∠A=∠DBE,
在△ABC和△BDE中,
,
∴△ABC≌△BDE(AAS),
∴AB=BD;
(2)∵∠A=62°,∠ABC=90°,
∴∠C=∠E=28°,
∵ED⊥BD,
∴∠BDE=90°,
∴∠DBE=62°,
∵∠DBC=34°,
∴∠FBE=28°,
∴∠BFE=180°﹣∠E﹣∠FBE=180°﹣28°﹣28°=124°.
22.如图,在△ABC中,∠ACB=90°,AC=BC,D是AB上一点,AE⊥CD,BF⊥CD,CH⊥AB.求证:BD=CG.21教育网
【解答】证明:∵AE⊥CD,BF⊥CD,
∴∠AEC=∠BFC=90°.
∵∠EAC+∠ACE=90°,∠ACE+∠BCF=90,
∴∠CAE=∠BCF.
在△ACE和△CBF中,,
△ACE≌△CBF(AAS).
∴CE=BF.
∵∠CDH与∠BDF是对顶角,
∴∠CDH=∠BDF.
∵∠CDH+∠ECG=90°,∠BDF+∠DBF=90°,
∴∠ECG=∠DBF.
在△CEG和△BFD中,
,
∴△CEG≌△BFD(ASA),
∴CG=BD.
23.已知:如图,AB∥CD,AD与BC相交于点O,且OA=OD,求证:OB=OC.
【解答】证明:∵AD与BC相交于点O,
∴∠AOB=∠DOC,
∵AB∥CD,
∴∠B=∠C,
在△AOB和△DOC中,
,
∴△AOB≌△DOC中(AAS),
∴OB=OC.
24.(2015秋?奉贤区期中)如图,已知在△ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE.21·cn·jy·com
(1)求证:DE∥BC;
(2)如果F是BC延长线上一点,且∠EBC=∠EFC,求证:DE=CF.
【解答】证明:(1)∵AB=AC,
∴∠ABC=∠ACB,
∵AD=AE,
∴∠ADE=∠AED,
∵∠A=∠A,
∴∠ADE=∠ABC,
∴DE∥BC;
(2)∵∠EBC=∠EFC,
∠ABC=∠ACB,
∴∠DBE+∠EBC=∠CEF+∠EFC,
∴∠DBE=∠CEF,∠DEB=∠EFC,
在△BDE与△EFC中,
,
∴△BDE≌△EFC(AAS),
∴DE=CF.
25.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)如图①,BF垂直CE于点F,交CD于点G,试说明AE=CG;
(2)如图②,作AH垂直于CE的延长线,垂足为H,交CD的延长线于点M,则图中与BE相等的线段是 CM ,并说明理由.21世纪教育网版权所有
【解答】(1)证明:∵点D是AB中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,
又∵BF⊥CE,
∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△AEC和△CGB中,
,
∴△AEC≌△CGB(ASA),
∴AE=CG;
(2)答:BE=CM
理由:∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
在△BCD和△ACD中,
,
∴△BCD≌△ACD(SAS),
∴∠ADC=∠CDB,
∵∠ADC+∠CDB=180°,
∴∠ADC=∠CDB=90°,
∴∠CBE=45°,
∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
在△BCE和△CAM中,
,
∴△BCE≌△CAM(AAS),
∴BE=CM.
故答案为:CM.
26.已知:如图,在△ABC中,∠BAC=90°,AB=AC,l是过点A的一条直线,BD⊥l,CE⊥l,垂足分别为D、E.
(1)如图①,求证:DE=BD+CE;
(2)若直线l绕A点旋转到图②位置时,其余条件不变,请把图形补充完整,写出BD、CE与DE之间的数量关系,并证明你的结论.
【解答】证明:(1)∵BD⊥l,CE⊥l,∴∠BDA=∠AEC=90°
又∵∠BAC=90°,∴∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,
∴∠CAE=∠ABD
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS)
∴BD=AE,AD=CE,
∵DE=AD+AE,∴DE=CE+BD;
(2)如图②所示:
结论:DE=CE﹣BD.
理由:∵BD⊥l,CE⊥l,
∴∠BDA=∠AEC=90°
∵∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,
∴∠CAE=∠ABD
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵DE=AD﹣AE,
∴DE=CE﹣BD.
27.如图,点D,E分别是ABC的边BC,AC上的点,BE,AD交于F,已知AB=AC,∠BAC=∠AFE=2∠ACB=2α,G为AC上的点,∠AEB=∠CGD.探究线段AE,GC的数量关系,并说明理由.
【解答】解:AE=CG,
理由:过C作CH⊥AC交AD的延长线与H,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠BAC=∠AFE=2∠ACB=2α,
∴∠ABC=∠ACB=α,
∵∠ABC+∠BAC+∠ACB=180°,
∴α+α+2α=180°,
∴α=45°,
∴∠BAC=∠AFE=90°,∠ABC=∠ACB=45°,
∴∠DCH=45°,
∵∠ABE+∠BAF=∠CAD+∠BAF=90°,
∴∠ABF=∠CAD,
在△ABE与△AHD中,
,
∴△ABE≌△ACH,
∴AE=CH,∠AEB=∠H,
∵∠AEF=∠DGC,
∴∠DGC=∠H,
在△DGC与△CHD中,
,
∴△DGC≌△CHD,
∴CG=CH,
∴AE=CG.
一.选择题(共15小题)
1.(2016春?成安县期末)在△ABC和△AˊB′C′中,已知∠A=∠A′,AB=A′B′,在下面判断中错误的是( )
A.若添加条件AC=A′C′,则△ABC≌△A′B′C′
B.若添加条件BC=B′C′,则△ABC≌△A′B′C′
C.若添加条件∠B=∠B′,则△ABC≌△A′B′C′
D.若添加条件∠C=∠C′,则△ABC≌△A′B′C′
2.如图,AB与CD相交于点E,AD=CB,若使△AED≌△CEB,则应补充的条件是( )
A.∠A=∠C B.AE=CE C.DE=BE D.不用补充条件
3.(2016?金华)如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )21cnjy.com
A.AC=BD B.∠CAB=∠DBA C.∠C=∠D D.BC=AD
4.(2015春?禅城区校级期末)下列条件中能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D B.∠A=∠D,∠B=∠E,∠C=∠F
C.AC=DF,∠B=∠F,AB=DE D.∠B=∠E,∠C=∠F,AC=DF
5.(2016春?毕节市校级期中)下列判断中错误的是( )
A.有两角和一边对应相等的两个三角形全等
B.有一边对应相等的两个等边三角形全等
C.有两边和其中一边上的中线对应相等的两个三角形全等
D.有两边和一角对应相等的两个三角形全等
6.(2016?武城县一模)如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )
A.① B.② C.①和② D.①②③
7.如图,在四边形ABCD中,AD∥BC,若∠DAB的平分线AE交CD于E,连接BE,且BE也平分∠ABC,则以下的命题中正确的个数是( )
①BC+AD=AB;②E为CD中点;③∠AEB=90°;④S△ABE=S四边形ABCD.
A.1 B.2 C.3 D.4
8.如图,A、B、C、D在同一条直线上,∠EAD=∠FAD,∠EDA=∠FDA,则图中共有全等三角形( )【版权所有:21教育】
A.3对 B.4对 C.5对 D.6对
9.如图,已知AB=CD,AD∥BC,∠ABC=∠DCB,则图中共有全等三角形( )
A.5对 B.4对 C.3对 D.2对
10.(2015春?高密市校级月考)如图所示,已知AB∥CD,AD∥BC,那么图中共有全等三角形( )21·世纪*教育网
A.1对 B.2对 C.4对 D.8对
11.(2015秋?南开区期末)在△ABC和△A′B′C′中,已知∠A=∠A′,AB=A′B′,添加下列条件中的一个,不能使△ABC≌△A′B′C′一定成立的是( )
A.AC=A′C′ B.BC=B′C′ C.∠B=∠B′ D.∠C=∠C′
12.(2015秋?蜀山区期末)如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )
A.AB=DE B.DF∥AC C.∠E=∠ABC D.AB∥DE
13.(2015?新泰市二模)如图所示,∠E=∠F,∠B=∠C,AE=AF,以下结论:①∠FAN=∠EAM;②EM=FN;③△ACN≌△ABM;④CD=DN.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
14.(2016?济南校级一模)如图,在△ABC与△DEF中,已有条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是( )
A.∠B=∠E,BC=EF B.BC=EF,AC=DF C.∠A=∠D,∠B=∠E D.∠A=∠D,BC=EF
15.(2016?黔西南州)如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE B.AC=DF C.∠A=∠D D.BF=EC
三.解答题(共13小题)
16.如图,已知:点B、E、F、C在同一直线上,∠A=∠D,BE=CF,且AB∥CD.求证:AF∥EDwww.21-cn-jy.com
证明:∵BE=FC
∴BE+EF=FC+EF( )
即:
∵AB∥CD
∴∠B=∠C( )
∠A=∠D
∠B=∠C
在△ABF和△DCE中,有
BF=CE
∴△ABF≌△DCE( )
∴∠AFB=∠DEC( )
∴AF∥ED( )
17.已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F,求证: 21*cnjy*com
(1)AC=2BF;
(2)AB垂直平分DF.
18.如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,D、E为垂足.求证:DE+BE=CE.
19.已知:如图,在Rt△ABC中,∠ACB=90°,∠B=60°,AD,CE是角平分线,AD与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为M,N.求证:FE=FD.
20.(2016?沛县校级一模)如图,在△ABC中,AD是△ABC的中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.
求证:BE=CF.
21.(2015秋?迁安市期中)如图,在△ABC中,∠A=62°,∠ABC=90°,点D在AC上,连接BD,过点D作ED⊥BD,垂足为D,使DE=BC,连接BE,若∠C=∠E.
(1)求证:AB=BD;
(2)若∠DBC=34°,求∠BFE的度数.
22.如图,在△ABC中,∠ACB=90°,AC=BC,D是AB上一点,AE⊥CD,BF⊥CD,CH⊥AB.求证:BD=CG.
23.已知:如图,AB∥CD,AD与BC相交于点O,且OA=OD,求证:OB=OC.
24.(2015秋?奉贤区期中)如图,已知在△ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE.
(1)求证:DE∥BC;
(2)如果F是BC延长线上一点,且∠EBC=∠EFC,求证:DE=CF.
25.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)如图①,BF垂直CE于点F,交CD于点G,试说明AE=CG;
(2)如图②,作AH垂直于CE的延长线,垂足为H,交CD的延长线于点M,则图中与BE相等的线段是 ,并说明理由.
26.已知:如图,在△ABC中,∠BAC=90°,AB=AC,l是过点A的一条直线,BD⊥l,CE⊥l,垂足分别为D、E.
(1)如图①,求证:DE=BD+CE;
(2)若直线l绕A点旋转到图②位置时,其余条件不变,请把图形补充完整,写出BD、CE与DE之间的数量关系,并证明你的结论.
27.如图,点D,E分别是ABC的边BC,AC上的点,BE,AD交于F,已知AB=AC,∠BAC=∠AFE=2∠ACB=2α,G为AC上的点,∠AEB=∠CGD.探究线段AE,GC的数量关系,并说明理由.
1.5三角形全等的判断(AAS)
参考答案与试题解析
一.选择题(共15小题)
1.(2016春?成安县期末)在△ABC和△AˊB′C′中,已知∠A=∠A′,AB=A′B′,在下面判断中错误的是( )
A.若添加条件AC=A′C′,则△ABC≌△A′B′C′
B.若添加条件BC=B′C′,则△ABC≌△A′B′C′
C.若添加条件∠B=∠B′,则△ABC≌△A′B′C′
D.若添加条件∠C=∠C′,则△ABC≌△A′B′C′
【解答】解:A,正确,符合SAS判定;
B,不正确,因为边BC与B′C′不是∠A与∠A′的一边,所以不能推出两三角形全等;
C,正确,符合AAS判定;
D,正确,符合ASA判定;
故选B.
2.如图,AB与CD相交于点E,AD=CB,若使△AED≌△CEB,则应补充的条件是( )
A.∠A=∠C B.AE=CE C.DE=BE D.不用补充条件
【解答】解:∵AD=CB,
而∠AED=∠BEC,
∴当∠A=∠C时,可判断△AED≌△CEB.
故选A.
3.(2016?金华)如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
A.AC=BD B.∠CAB=∠DBA C.∠C=∠D D.BC=AD
【解答】解:由题意,得∠ABC=∠BAD,AB=BA,
A、∠ABC=∠BAD,AB=BA,AC=BD,(SSA)三角形不全等,故A错误;
B、在△ABC与△BAD中,,△ABC≌△BAD(ASA),故B正确;
C、在△ABC与△BAD中,,△ABC≌△BAD(AAS),故C正确;
D、在△ABC与△BAD中,,△ABC≌△BAD(SAS),故D正确;
故选:A.
4.(2015春?禅城区校级期末)下列条件中能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D B.∠A=∠D,∠B=∠E,∠C=∠F
C.AC=DF,∠B=∠F,AB=DE D.∠B=∠E,∠C=∠F,AC=DF
【解答】解:
A、根据AB=DE,BC=EF,∠A=∠D,不能判断△ABC≌△DEF,故本选项错误;
B、根据∠A=∠D,∠B=∠E,∠C=∠F,不能判断△ABC≌△DEF,故本选项错误;
C、根据AC=DF,∠B=∠F,AB=DE,不能判断△ABC≌△DEF,故本选项错误;
D、∵在△ABC和△DEF中
,
∴△ABC≌△DEF(AAS),故本选项正确;
故选D.
5.(2016春?毕节市校级期中)下列判断中错误的是( )
A.有两角和一边对应相等的两个三角形全等
B.有一边对应相等的两个等边三角形全等
C.有两边和其中一边上的中线对应相等的两个三角形全等
D.有两边和一角对应相等的两个三角形全等
【解答】解:A、有两角和一边对应相等的两个三角形全等,说法正确;
B、有一边对应相等的两个等边三角形全等,说法正确;
C、有两边和其中一边上的中线对应相等的两个三角形全等,说法正确;
D、有两边和一角对应相等的两个三角形全等,说法错误;
故选:D.
6.(2016?武城县一模)如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )【来源:21cnj*y.co*m】
A.① B.② C.①和② D.①②③
【解答】解:如图,连接AD;
在△ABE与△ACF中,
,
∴△ABE≌△ACF(SAS);
∴∠B=∠C;
∵AB=AC,AE=AF,
∴BF=CE;
在△CDE与△BDF中,
,
∴△CDE≌△BDF(AAS),
∴DC=DB;
在△ADC与△ADB中,
,
∴△ADC≌△ADB(SAS),
∴∠CAD=∠BAD;
综上所述,①②③均正确,
故选D
7.如图,在四边形ABCD中,AD∥BC,若∠DAB的平分线AE交CD于E,连接BE,且BE也平分∠ABC,则以下的命题中正确的个数是( )【来源:21·世纪·教育·网】
①BC+AD=AB;②E为CD中点;③∠AEB=90°;④S△ABE=S四边形ABCD.
A.1 B.2 C.3 D.4
【解答】解:在AB上截取AF=AD.
则△AED≌△AEF(SAS).
∴∠AFE=∠D.
∵AD∥BC,∴∠D+∠C=180°.
∴∠C=∠BFE.
∴△BEC≌△BEF(AAS).
∴①BC=BF,故AB=BC+AD;
②CE=EF=ED,即E是CD中点;
③∠AEB=∠AEF+∠BEF=∠DEF+∠CEF=×180°=90°;
④S△AEF=S△AED,S△BEF=S△BEC,
∴S△AEB=S四边形BCEF+S四边形EFAD=S四边形ABCD.
故选D.
8.如图,A、B、C、D在同一条直线上,∠EAD=∠FAD,∠EDA=∠FDA,则图中共有全等三角形( )www-2-1-cnjy-com
A.3对 B.4对 C.5对 D.6对
【解答】解析:在△ADE与△ADF中,
,
∴△ADE≌△ADF(ASA);
∴AE=AF,DE=DF;
同理可证:△ABE≌ABF;△ACE≌△ACF;△DCE≌△DCF;△BCE≌△BCF;△BDE≌△BDF,综上所述,图中共有全等三角形6对,2-1-c-n-j-y
故选D.
9.如图,已知AB=CD,AD∥BC,∠ABC=∠DCB,则图中共有全等三角形( )
A.5对 B.4对 C.3对 D.2对
【解答】解:在△ABC和△DCB中,
,
∴△ABC≌△DCB(SAS),
∴∠ACB=∠DBC,AC=BD,
∵AD∥BC,
∴∠ADB=∠DBC,∠DAC=∠ACB,
∴∠DAC=∠ADB,
在△ADC和△DAB中,
,
∴△ADC≌△DAB(SAS),
∴∠ABD=∠DCA,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(AAS),
故选:C.
10.(2015春?高密市校级月考)如图所示,已知AB∥CD,AD∥BC,那么图中共有全等三角形( )【出处:21教育名师】
A.1对 B.2对 C.4对 D.8对
【解答】解:全等三角形有△ABD≌△CDB,△ACD≌△CAB,△AOD≌△COB,△AOB≌△COD,共4对,
故选C.
11.(2015秋?南开区期末)在△ABC和△A′B′C′中,已知∠A=∠A′,AB=A′B′,添加下列条件中的一个,不能使△ABC≌△A′B′C′一定成立的是( )
A.AC=A′C′ B.BC=B′C′ C.∠B=∠B′ D.∠C=∠C′
【解答】解:
A、∠A=∠A′,AB=A′B′AC=A′C′,根据SAS能推出△ABC≌△A′B′C′,故A选项错误;
B、具备∠A=∠A′,AB=A′B′,BC=B′C′,不能判断△ABC≌△A′B′C′,故B选项正确;
C、根据ASA能推出△ABC≌△A′B′C′,故C选项错误;
D、根据AAS能推出△ABC≌△A′B′C′,故D选项错误.
故选:B.
12.(2015秋?蜀山区期末)如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )
A.AB=DE B.DF∥AC C.∠E=∠ABC D.AB∥DE
【解答】解:A、添加DE=AB与原条件满足SSA,不能证明△ABC≌△DEF,故A选项正确.
B、添加DF∥AC,可得∠DFE=∠ACB,根据AAS能证明△ABC≌△DEF,故B选项错误.
C、添加∠E=∠ABC,根据AAS能证明△ABC≌△DEF,故C选项错误.
D、添加AB∥DE,可得∠E=∠ABC,根据AAS能证明△ABC≌△DEF,故D选项错误.
故选:A.
13.(2015?新泰市二模)如图所示,∠E=∠F,∠B=∠C,AE=AF,以下结论:①∠FAN=∠EAM;②EM=FN;③△ACN≌△ABM;④CD=DN.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:在△ABE和△ACF中,
,
∴△ABE≌△ACF(AAS),
∴∠BAE=∠CAF,
∴∠FAN=∠EAM,
∴①正确;
在△AEM和△AFN中,
,
∴△AEM≌△AFN(ASA),
∴EM=FN,AM=AN,
∴②正确;
在△ACN和△ABM中,
,
∴△ACN≌△ABM(AAS),
∴③正确,
④不正确;
正确的结论有3个.
故选:C.
14.(2016?济南校级一模)如图,在△ABC与△DEF中,已有条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是( )21教育名师原创作品
A.∠B=∠E,BC=EF B.BC=EF,AC=DF C.∠A=∠D,∠B=∠E D.∠A=∠D,BC=EF
【解答】解:(1)在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS);故A正确;
(2)在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS);故B正确;
(3)在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA);故C正确;
(4)无法证明△ABC≌△DEF,故D错误;
故选 D.
15.(2016?黔西南州)如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE B.AC=DF C.∠A=∠D D.BF=EC
【解答】解:解:选项A、添加AB=DE可用AAS进行判定,故本选项错误;
选项B、添加AC=DF可用AAS进行判定,故本选项错误;
选项C、添加∠A=∠D不能判定△ABC≌△DEF,故本选项正确;
选项D、添加BF=EC可得出BC=EF,然后可用ASA进行判定,故本选项错误.
故选C.
三.解答题(共13小题)
16.如图,已知:点B、E、F、C在同一直线上,∠A=∠D,BE=CF,且AB∥CD.求证:AF∥ED
证明:∵BE=FC
∴BE+EF=FC+EF( 等式的性质 )
即: BF=CE
∵AB∥CD
∴∠B=∠C( 两直线平行内错角相等 )
∠A=∠D
∠B=∠C
在△ABF和△DCE中,有
BF=CE
∴△ABF≌△DCE( AAS )
∴∠AFB=∠DEC( 全等三角形对应角相等 )
∴AF∥ED( 内错角相等两直线平行 )
【解答】证明:∵BE=FC,
∴BE+EF=FC+EF(等式的性质),
即BF=CE,
∵AB∥CD,
∴∠B=∠C(两直线平行内错角相等),
∠A=∠D,
∠B=∠C,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(AAS),
∴∠AFB=∠DEC(全等三角形对应角相等),
∴AF∥ED(内错角相等两直线平行).
故答案为:等式的性质;BF=CE;两直线平行内错角相等;AAS;全等三角形对应角相等;内错角相等两直线平行
17.已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F,求证:
(1)AC=2BF;
(2)AB垂直平分DF.
【解答】证明:(1)∵BF∥AC,
∴BC⊥BF,
∵∠DCE+∠F=90°,∠DCE+∠CDA=90°,
∴∠CDA=∠F,
在△ACD和△CBF中,
,
∴△ACD≌△CBF(AAS),
∴CD=BF,
∵点D是BC的中点,
∴AC=BC=2CD,
∴AC=2BF;
(2)连接DF交AB于G点,
∵点D是BC的中点,
∴AC=2BD,
∵AC=2BF,
∴BD=BF,
∵AC=BC,∠ACB=90°,
∴∠ABC=45°,
∵△ACD≌△CBF,
∴∠CBF=∠ACD=90°,
∴∠ABF=45°,
在△DBG和△FBG中,
,
∴△DBG≌△FBG(SAS),
∴DG=FG,∠DGB=∠FGB,
∵∠DGB+∠FGB=180°,
∴∠DGB=∠FGB=90°,
∴AB垂直平分DF.
18.如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,D、E为垂足.求证:DE+BE=CE.2·1·c·n·j·y
【解答】证明:∵∠ACB=90°,BE⊥CE,AD⊥CE,
∴∠BEC=∠ACB=∠ADC=90°,
∴∠ACE+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中
,
∴△ADC≌△CEB(AAS).
∴BE=CD,
∴CE=CD+DE=DE+BE.
19.已知:如图,在Rt△ABC中,∠ACB=90°,∠B=60°,AD,CE是角平分线,AD与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为M,N.求证:FE=FD.
【解答】证明:连接BF,
∵F是角平分线交点,
∴BF也是角平分线,
∴MF=FN,∠DNF=∠EMF=90°,
∵在Rt△ABC中,∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∴∠DAC=∠BAC=15°,
∴∠CDA=75°,
∵∠NFC=45°,∠MFN=120°,
∴∠MFE=15°,
∴∠MEF=75°=∠NDF,
在△DNF和△EMF中,
,
∴△DNF≌△EMF(AAS),
∴FE=FD.
20.(2016?沛县校级一模)如图,在△ABC中,AD是△ABC的中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.21*cnjy*com
求证:BE=CF.
【解答】解:∵BE⊥AE,CF⊥AE,
∴∠BED=∠CFD=90°,
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS),
∴BE=CF.
21.(2015秋?迁安市期中)如图,在△ABC中,∠A=62°,∠ABC=90°,点D在AC上,连接BD,过点D作ED⊥BD,垂足为D,使DE=BC,连接BE,若∠C=∠E.
(1)求证:AB=BD;
(2)若∠DBC=34°,求∠BFE的度数.
【解答】解:(1)∵∠ABC=90°,
∴∠A+∠C=90°,
∵ED⊥BD,
∴∠BDE=90°,
∵∠C=∠E,
∴∠A=∠DBE,
在△ABC和△BDE中,
,
∴△ABC≌△BDE(AAS),
∴AB=BD;
(2)∵∠A=62°,∠ABC=90°,
∴∠C=∠E=28°,
∵ED⊥BD,
∴∠BDE=90°,
∴∠DBE=62°,
∵∠DBC=34°,
∴∠FBE=28°,
∴∠BFE=180°﹣∠E﹣∠FBE=180°﹣28°﹣28°=124°.
22.如图,在△ABC中,∠ACB=90°,AC=BC,D是AB上一点,AE⊥CD,BF⊥CD,CH⊥AB.求证:BD=CG.21教育网
【解答】证明:∵AE⊥CD,BF⊥CD,
∴∠AEC=∠BFC=90°.
∵∠EAC+∠ACE=90°,∠ACE+∠BCF=90,
∴∠CAE=∠BCF.
在△ACE和△CBF中,,
△ACE≌△CBF(AAS).
∴CE=BF.
∵∠CDH与∠BDF是对顶角,
∴∠CDH=∠BDF.
∵∠CDH+∠ECG=90°,∠BDF+∠DBF=90°,
∴∠ECG=∠DBF.
在△CEG和△BFD中,
,
∴△CEG≌△BFD(ASA),
∴CG=BD.
23.已知:如图,AB∥CD,AD与BC相交于点O,且OA=OD,求证:OB=OC.
【解答】证明:∵AD与BC相交于点O,
∴∠AOB=∠DOC,
∵AB∥CD,
∴∠B=∠C,
在△AOB和△DOC中,
,
∴△AOB≌△DOC中(AAS),
∴OB=OC.
24.(2015秋?奉贤区期中)如图,已知在△ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE.21·cn·jy·com
(1)求证:DE∥BC;
(2)如果F是BC延长线上一点,且∠EBC=∠EFC,求证:DE=CF.
【解答】证明:(1)∵AB=AC,
∴∠ABC=∠ACB,
∵AD=AE,
∴∠ADE=∠AED,
∵∠A=∠A,
∴∠ADE=∠ABC,
∴DE∥BC;
(2)∵∠EBC=∠EFC,
∠ABC=∠ACB,
∴∠DBE+∠EBC=∠CEF+∠EFC,
∴∠DBE=∠CEF,∠DEB=∠EFC,
在△BDE与△EFC中,
,
∴△BDE≌△EFC(AAS),
∴DE=CF.
25.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)如图①,BF垂直CE于点F,交CD于点G,试说明AE=CG;
(2)如图②,作AH垂直于CE的延长线,垂足为H,交CD的延长线于点M,则图中与BE相等的线段是 CM ,并说明理由.21世纪教育网版权所有
【解答】(1)证明:∵点D是AB中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,
又∵BF⊥CE,
∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△AEC和△CGB中,
,
∴△AEC≌△CGB(ASA),
∴AE=CG;
(2)答:BE=CM
理由:∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
在△BCD和△ACD中,
,
∴△BCD≌△ACD(SAS),
∴∠ADC=∠CDB,
∵∠ADC+∠CDB=180°,
∴∠ADC=∠CDB=90°,
∴∠CBE=45°,
∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
在△BCE和△CAM中,
,
∴△BCE≌△CAM(AAS),
∴BE=CM.
故答案为:CM.
26.已知:如图,在△ABC中,∠BAC=90°,AB=AC,l是过点A的一条直线,BD⊥l,CE⊥l,垂足分别为D、E.
(1)如图①,求证:DE=BD+CE;
(2)若直线l绕A点旋转到图②位置时,其余条件不变,请把图形补充完整,写出BD、CE与DE之间的数量关系,并证明你的结论.
【解答】证明:(1)∵BD⊥l,CE⊥l,∴∠BDA=∠AEC=90°
又∵∠BAC=90°,∴∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,
∴∠CAE=∠ABD
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS)
∴BD=AE,AD=CE,
∵DE=AD+AE,∴DE=CE+BD;
(2)如图②所示:
结论:DE=CE﹣BD.
理由:∵BD⊥l,CE⊥l,
∴∠BDA=∠AEC=90°
∵∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,
∴∠CAE=∠ABD
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵DE=AD﹣AE,
∴DE=CE﹣BD.
27.如图,点D,E分别是ABC的边BC,AC上的点,BE,AD交于F,已知AB=AC,∠BAC=∠AFE=2∠ACB=2α,G为AC上的点,∠AEB=∠CGD.探究线段AE,GC的数量关系,并说明理由.
【解答】解:AE=CG,
理由:过C作CH⊥AC交AD的延长线与H,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠BAC=∠AFE=2∠ACB=2α,
∴∠ABC=∠ACB=α,
∵∠ABC+∠BAC+∠ACB=180°,
∴α+α+2α=180°,
∴α=45°,
∴∠BAC=∠AFE=90°,∠ABC=∠ACB=45°,
∴∠DCH=45°,
∵∠ABE+∠BAF=∠CAD+∠BAF=90°,
∴∠ABF=∠CAD,
在△ABE与△AHD中,
,
∴△ABE≌△ACH,
∴AE=CH,∠AEB=∠H,
∵∠AEF=∠DGC,
∴∠DGC=∠H,
在△DGC与△CHD中,
,
∴△DGC≌△CHD,
∴CG=CH,
∴AE=CG.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
