2.6直角三角形同步练习

2.6直角三角形同步练习
一．选择题（共9小题）
1．（2016?昆明校级模拟）如图，BD平分∠ABC，CD⊥BD，D为垂足，∠C=55°，则∠ABC的度数是（　　）　　21*cnjy*com
A．35° B．55° C．60° D．70°
2．（2016?石家庄校级模拟）如图，∠AOB=40°，OC平分∠AOB，直尺与OC垂直，则∠1等于（　　）【来源：21cnj*y.co*m】
A．60° B．70° C．50° D．40°
3．（2016春?湘潭期末）如图，Rt△ABC中，∠ACB=90°，∠A=55°，将其折叠，使点A落在边CB上A′处，折痕为CD，则∠A′DB=（　　）
A．40° B．30° C．20° D．10°
4．（2016春?高青县期中）如图，∠ACB=90°，CD⊥AB，垂足为D，下列结论错误的是（　　）
A．图中有三个直角三角形 B．∠1=∠2
C．∠1和∠B都是∠A的余角 D．∠2=∠A
5．（2016春?东台市期中）如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处，若∠A=25°，则∠BDC等于（　　）
A．44° B．60° C．67° D．70°
6． 将一副直角三角尺如图放置，若∠AOD=20°，则∠BOC的大小为（　　）
A．140° B．160° C．170° D．150°
7． 如果一个三角形的一个顶点是它的三条高的交点，那么这个三角形是（　　）
A．锐角三角形 B．直角三角形 C．钝角三角形 D．等边三角形
8． 如图，已知△ABC中，∠ACB=90°，CD为AB边上的高，∠ABC的平分线BE分别交CD、CA于点F、E，则下列结论正确的有（　　）21教育网
①∠CFE=∠CEF；②∠FCB=∠FBC，③∠A=∠DCB；④∠CFE与∠CBF互余．
A．①③④ B．②③④ C．①②④ D．①②③
9． 如图，在△ABC中，∠BAC=90°，AC≠AB，AD是斜边BC上的高，DE⊥AC，DF⊥AB，垂足分别为E、F，则图中与∠C（∠C除外）相等的角的个数是（　　）
A．3个 B．4个 C．5个 D．6个
　
二．填空题（共10小题）
10．如图，△ABC中，∠ACB=90°，CD⊥AB于D，若∠A=30°，则∠1=______度，∠2=______度，∠B=______度．
11．如图，在Rt△ABC中，∠C=90°，ED⊥AB．求证：∠AED=∠B．
证明：在Rt△ABC中，∠A+∠B=90°（根据是______）
在Rt△ADE中，∠A+∠AED=90°（根据是______）
所以∠AED=∠B（根据是______）
12． 如图，Rt△ABC中，∠ACB=90°，CD⊥AB，DE⊥AC，则图中共有______个直角三角形．
13． 直角三角形中两个锐角的差为20°，则两个锐角的度数分别是______．
14． 在△ABC中，AB边上的中线CD=3，AB=6，BC+AC=8，则△ABC的面积为______．
15． 如图，△ABC中，∠C=90°，∠B=30°，AD是∠BAC的平分线，DE⊥AB，垂足为E，则∠ADE的度数是______．
16．（2016春?平定县期中）已知点D是Rt△ABC斜边AB上的中点，∠B=65°，那么∠ACD=______度．
17．（2016春?郴州校级月考）直角三角形的两直角边分别为12和24，则斜边上的中线长为______，斜边上的高为______．
18．（2015秋?南京期中）如图，在△ABC中，∠ACB=90°，∠CAB=30°．以AB长为一边作△ABD，且AD=BD，∠ADB=90°，取AB中点E，连DE、CE、CD．则∠EDC=______°．
19． 如图，点E是Rt△ABC、Rt△ABD的斜边AB的中点，AC=BC，∠DBA=20°，那么∠DCE的度数是______．
三．解答题（共10小题）
20． 操作发现
将一副直角三角板如图（1）摆放，能够发现等腰直角三角板ABC的斜边BC与含30°角的直角三角板DEF的长直角边DE重合．2·1·c·n·j·y
问题解决
将图1中的等腰直角三角板ABC绕点B顺时针旋转30°，点C落在BF上．AC与BD交于点O，连接CD，如图2．
（1）若DF=4，求BF的长；
（2）求证：△CDO是等腰三角形．
21． 阅读理解：
如图1，在△ABC的边AB上取一点P，连接CP，可以把△ABC分成两个三角形，如果这两个三角形都是等腰三角形，我们就称点P是△ABC的边AB上的和谐点．
解决问题：
（1）如图2，△ABC中，∠ACB=90°，试找出边AB上的和谐点P，并说明理由．
（2）已知∠A=40°，△ABC的顶点B在射线l上（图3），点P是边AB上的和谐点，请在图3中画出所有符合条件的B点，并写出相应的∠B的度数．
22． 如图，∠ABC=90°，D、E分别在BC、AC上，AD⊥DE，且AD=DE，点F是AE的中点，FD与AB相交于点M．
（1）求证：∠FMC=∠FCM；
（2）AD与MC垂直吗？并说明理由．
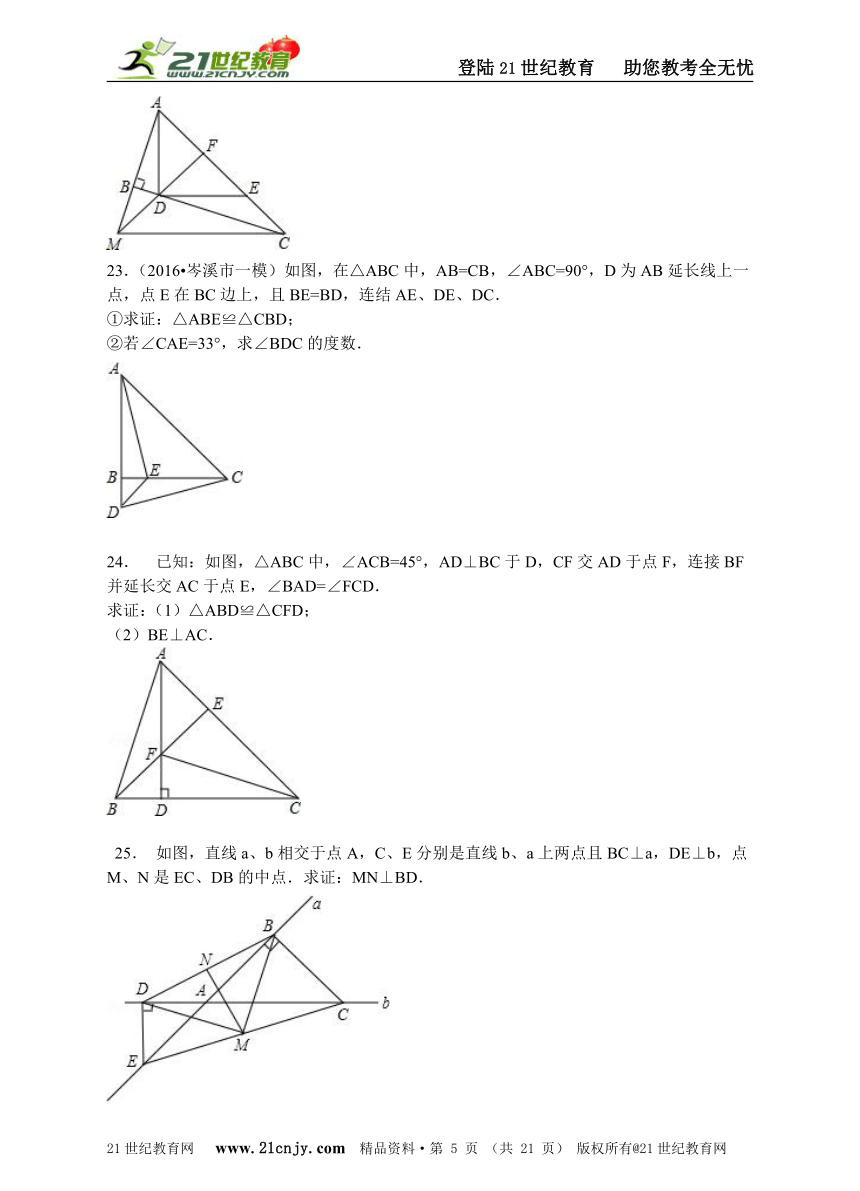
23．（2016?岑溪市一模）如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连结AE、DE、DC．
①求证：△ABE≌△CBD；
②若∠CAE=33°，求∠BDC的度数．
　
24． 已知：如图，△ABC中，∠ACB=45°，AD⊥BC于D，CF交AD于点F，连接BF并延长交AC于点E，∠BAD=∠FCD．
求证：（1）△ABD≌△CFD；
（2）BE⊥AC．
　
25． 如图，直线a、b相交于点A，C、E分别是直线b、a上两点且BC⊥a，DE⊥b，点M、N是EC、DB的中点．求证：MN⊥BD．
26． 如图，在△ABC中，点D在AB上，且CD=CB，点E为BD的中点，点F为AC的中点，连结EF交CD于点M，连接AM．21教育名师原创作品
（1）求证：EF=AC．
（2）若∠BAC=45°，求线段AM、DM、BC之间的数量关系．
27． 如图，在四边形ABCD中，∠BAD=∠BCD=90°，O为BD的中点，∠OAC和∠OCA相等吗？请说明理由．
28． 如图，△ABC中，AD是边BC上的高，CF是边AB上的中线，且DC=BF，DE⊥CF于E．
（1）E是CF的中点吗？试说明理由；
（2）试说明：∠B=2∠BCF．
　
29．（2016春?深圳校级期中）如图，在△ACB中，∠ACB=90゜，CD⊥AB于D．
（1）求证：∠ACD=∠B；
（2）若AF平分∠CAB分别交CD、BC于E、F，求证：∠CEF=∠CFE．
　

2.6直角三角形同步练习
参考答案与试题解析
　
一．选择题（共9小题）
1．（2016?昆明校级模拟）如图，BD平分∠ABC，CD⊥BD，D为垂足，∠C=55°，则∠ABC的度数是（　　）
A．35° B．55° C．60° D．70°
【解答】解：∵CD⊥BD，∠C=55°，
∴∠CBD=90°﹣55°=35°，
∵BD平分∠ABC，
∴∠ABC=2∠CBD=2×35°=70°．
故选D．
　
2．（2016?石家庄校级模拟）如图，∠AOB=40°，OC平分∠AOB，直尺与OC垂直，则∠1等于（　　）2-1-c-n-j-y
A．60° B．70° C．50° D．40°
【解答】解：如图所示：
根据题意得：∠1=∠2=∠3，
∵OC平分∠AOB，
∴∠AOC=∠AOB=20°，
∴∠3=90°﹣20°=70°，
∴∠1=70°；
故选：B．
　
3．（2016春?湘潭期末）如图，Rt△ABC中，∠ACB=90°，∠A=55°，将其折叠，使点A落在边CB上A′处，折痕为CD，则∠A′DB=（　　）
A．40° B．30° C．20° D．10°
【解答】解：在Rt△ABC中，∠ACB=90°，∠A=55°，
∴∠B=180°﹣90°﹣55°=35°，
由折叠可得：∠CA′D=∠A=55°，
又∵∠CA′D为△A′BD的外角，
∴∠CA′D=∠B+∠A′DB，
则∠A′DB=55°﹣35°=20°．
故选：C．
　
4．（2016春?高青县期中）如图，∠ACB=90°，CD⊥AB，垂足为D，下列结论错误的是（　　）
A．图中有三个直角三角形 B．∠1=∠2
C．∠1和∠B都是∠A的余角 D．∠2=∠A
【解答】解：∵∠ACB=90°，CD⊥AB，垂足为D，
∴△ACD∽△CBD∽△ABC．
A、∵图中有三个直角三角形Rt△ACD、Rt△CBD、Rt△ABC；故本选项正确；
B、应为∠1=∠B、∠2=∠A；故本选项错误；
C、∵∠1=∠B、∠2=∠A，而∠B是∠A的余角，∴∠1和∠B都是∠A的余角；故本选项正确；
D、∵∠2=∠A；故本选项正确．
故选B．
　
5．（2016春?东台市期中）如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处，若∠A=25°，则∠BDC等于（　　）21cnjy.com
A．44° B．60° C．67° D．70°
【解答】解：∵△ABC中，∠ACB=90°，∠A=25°，
∴∠B=90°﹣∠A=65°，
由折叠的性质可得：∠CED=∠B=65°，∠BDC=∠EDC，
∴∠ADE=∠CED﹣∠A=40°，
∴∠BDC=（180°﹣∠ADE）=70°．
故选D．
　
6． 将一副直角三角尺如图放置，若∠AOD=20°，则∠BOC的大小为（　　）
A．140° B．160° C．170° D．150°
【解答】解：∵将一副直角三角尺如图放置，∠AOD=20°，
∴∠COA=90°﹣20°=70°，
∴∠BOC=90°+70°=160°．
故选：B．
　
7． 如果一个三角形的一个顶点是它的三条高的交点，那么这个三角形是（　　）
A．锐角三角形 B．直角三角形 C．钝角三角形 D．等边三角形
【解答】解：A、锐角三角形，三条高线交点在三角形内，故错误；
B、因为直角三角形的直角所在的顶点正好是三条高线的交点，所以可以得出这个三角形是直角三角形，故正确；21·cn·jy·com
C、钝角三角形，三条高线不会交于一个顶点，故错误；
D、等边三角形，三条高线交点在三角形内，故错误．
故选B．
　
8． 如图，已知△ABC中，∠ACB=90°，CD为AB边上的高，∠ABC的平分线BE分别交CD、CA于点F、E，则下列结论正确的有（　　）www.21-cn-jy.com
①∠CFE=∠CEF；②∠FCB=∠FBC，③∠A=∠DCB；④∠CFE与∠CBF互余．
A．①③④ B．②③④ C．①②④ D．①②③
【解答】解：如图所示，
①∵BE平分∠ABC，
∴∠5=∠6，
∵∠3+∠4=90°，∠A+∠3=90°，
∴∠A=∠4，
∵∠1=∠A+∠6，∠2=∠4+∠5，
∠1=∠2，
故∠CFE=∠CEF，所以①正确；
②若∠FCB=∠FBC，即∠4=∠5，
由（1）可知：∠A=∠4，
∴∠A=∠5=∠6，
∵∠A+∠5+∠6=180°，
∴∠A=30°，
即只有当∠A=30°时，∠FCB=∠FBC而已知没有这个条件，故②错误；
③∵∠3+∠4=90°，∠A+∠3=90°，
∴∠A=∠4，
即∠A=∠DCB，故③正确；
④∵∠1=∠2，∠1+∠5=90°，
∴∠2+∠5=90°，
即：∠CFE与∠CBF互余，故④正确．
故选A．
　
9． 如图，在△ABC中，∠BAC=90°，AC≠AB，AD是斜边BC上的高，DE⊥AC，DF⊥AB，垂足分别为E、F，则图中与∠C（∠C除外）相等的角的个数是（　　）
A．3个 B．4个 C．5个 D．6个
【解答】解：如图，∵AD是斜边BC上的高，DE⊥AC，DF⊥AB，
∴∠C+∠B=90°，∠BDF+∠B=90°，∠BAD+∠B=90°，
∴∠C=∠BDF=∠BAD，
∵∠DAC+∠C=90°，∠DAC+∠ADE=90°，
∴∠C=∠ADE，
∴图中与∠C（除之C外）相等的角的个数是3，
故选：A．
　
二．填空题（共10小题）
10．如图，△ABC中，∠ACB=90°，CD⊥AB于D，若∠A=30°，则∠1=　60　度，∠2=　30　度，∠B=　60　度．【来源：21·世纪·教育·网】
【解答】解：∵∠ACB=90°，CD⊥AB于D，∠A=30°
∴∠1=90°﹣30°=60°；
∠2=90°﹣∠1=30°；
∠B=90°﹣∠A=60°．
　
11．如图，在Rt△ABC中，∠C=90°，ED⊥AB．求证：∠AED=∠B．
证明：在Rt△ABC中，∠A+∠B=90°（根据是　直角三角形两锐角互余　）
在Rt△ADE中，∠A+∠AED=90°（根据是　直角三角形两锐角互余　）
所以∠AED=∠B（根据是　等量代换　）
【解答】解：
在Rt△ABC和Rt△ADE中，由直角三角形两锐角互余可得到∠A+∠B=90°和∠A+∠AED=90°，【出处：21教育名师】
再利用等量代换可得到∠AED=∠B，
故答案为：直角三角形两锐角互余；直角三角形两锐角互余；等量代换．
　
12． 如图，Rt△ABC中，∠ACB=90°，CD⊥AB，DE⊥AC，则图中共有　5　个直角三角形．【版权所有：21教育】
【解答】解：∵∠ACB=90°，CD⊥AB，DE⊥AC，
∴△ABC，△ADC，△CDB，△CED，△AED为直角三角形，
∴共有五个直角三角形．
　
13． 直角三角形中两个锐角的差为20°，则两个锐角的度数分别是　55°、35°　．
【解答】解：设一个锐角为x，则另一个锐角为x﹣20°，
则x+x﹣20°=90°，
解得，x=55°，
x﹣20°=35°
故答案为：55°、35°．
　
14． 在△ABC中，AB边上的中线CD=3，AB=6，BC+AC=8，则△ABC的面积为　7　．
【解答】解：如图，在△ABC中，CD是AB边上的中线，
∵CD=3，AB=6，
∴AD=DB=3，
∴CD=AD=DB，
∴∠1=∠2，∠3=∠4，
∵∠1+∠2+∠3+∠4=180°，
∴∠1+∠3=90°，
∴△ABC是直角三角形，
∴AC2+BC2=AB2=36，
又∵AC+BC=8，
∴AC2+2AC?BC+BC2=64，
∴2AC?BC=64﹣（AC2+BC2）=64﹣36=28，
又∵S△ABC=AC?BC，
∴S△ABC==7．
　
15． 如图，△ABC中，∠C=90°，∠B=30°，AD是∠BAC的平分线，DE⊥AB，垂足为E，则∠ADE的度数是　60°　．
【解答】解：∵∠C=90°，∠B=30°，
∴∠BAC=60°，
AD是∠BAC的平分线，
∴∠EAD=∠BAC=30°，
∵DE⊥AB，
∴∠ADE=90°﹣30°=60°，
故答案为：60°．
　
16．（2016春?平定县期中）已知点D是Rt△ABC斜边AB上的中点，∠B=65°，那么∠ACD=　25　度．
【解答】解：如图，在Rt△ABC中，∠B=65°，
则∠A=25°，
∵点D是Rt△ABC斜边AB上的中点，
∴DA=DC，
∴∠ACD=∠A=25°，
故答案为：25．
　
17．（2016春?郴州校级月考）直角三角形的两直角边分别为12和24，则斜边上的中线长为　6　，斜边上的高为　　．
【解答】解：由勾股定理得，斜边长为=12，
则斜边上的中线长为12=6，
设斜边上的高为h，
则12×h=×12×24，
解得h=．
故答案为：6；．
　
18． 如图，在△ABC中，∠ACB=90°，∠CAB=30°．以AB长为一边作△ABD，且AD=BD，∠ADB=90°，取AB中点E，连DE、CE、CD．则∠EDC=　75　°．
【解答】解：∵∠ACB=90°，点E是AB中点，
∴EC=EA=EB=AB，
∴∠ECA=∠CAB=30°，
∴∠CEB=60°，
∵AD=BD，点E是AB中点，
∴DE⊥AB，即∠AED=90°，
∴∠DEC=180°﹣90°﹣60°=30°，
∵∠ADB=90°，点E是AB中点，
∴DE=AB，
∴ED=EC，
∴∠EDC=75°，
故答案为：75．
　
19． 如图，点E是Rt△ABC、Rt△ABD的斜边AB的中点，AC=BC，∠DBA=20°，那么∠DCE的度数是　25°　．21·世纪*教育网
【解答】解：∵点E是Rt△ABD的斜边AB的中点，
∴ED=EB=AB，
∴∠EDB=∠DBA=20°，
∴∠DEA=∠EDB+∠DBA=40°，
∵点E是Rt△ABC的斜边AB的中点，AC=BC，
∴EC=AB，CE⊥AB，
∴∠DEC=130°，ED=EC，
∴∠DCE=25°，
故答案为：25°．
三．解答题（共10小题）
20． 操作发现
将一副直角三角板如图（1）摆放，能够发现等腰直角三角板ABC的斜边BC与含30°角的直角三角板DEF的长直角边DE重合．
问题解决
将图1中的等腰直角三角板ABC绕点B顺时针旋转30°，点C落在BF上．AC与BD交于点O，连接CD，如图2．
（1）若DF=4，求BF的长；
（2）求证：△CDO是等腰三角形．
【解答】解：（1）∵在Rt△DEF中，∠DEF=30°，∠EDF=90°，DF=4，
∴BF=8．
（2）∵在△BDC 中，BC=DE，
∴∠BDC=∠BCD．
∵∠DEF=30°，
∴∠BDC=∠BCD=75°，
∵∠ACB=45°，
∴∠DOC=30°+45°=75°．
∴∠DOC=∠BDC，
∴△CDO是等腰三角形．
　
21． 阅读理解：
如图1，在△ABC的边AB上取一点P，连接CP，可以把△ABC分成两个三角形，如果这两个三角形都是等腰三角形，我们就称点P是△ABC的边AB上的和谐点．
解决问题：
（1）如图2，△ABC中，∠ACB=90°，试找出边AB上的和谐点P，并说明理由．
（2）已知∠A=40°，△ABC的顶点B在射线l上（图3），点P是边AB上的和谐点，请在图3中画出所有符合条件的B点，并写出相应的∠B的度数．
【解答】解：（1）AB边上的和谐点为AB的中点；理由如下：
∵P是AB的中点，
∴PC=AB=PA=PB，
∴△ACP和△BCP是等腰三角形；
（2）所有符合条件的点B有3个，如图3所示：∠B的度数为35°、50°、80°．
　
22． 如图，∠ABC=90°，D、E分别在BC、AC上，AD⊥DE，且AD=DE，点F是AE的中点，FD与AB相交于点M．21*cnjy*com
（1）求证：∠FMC=∠FCM；
（2）AD与MC垂直吗？并说明理由．
【解答】（1）证明：∵△ADE是等腰直角三角形，F是AE中点，
∴DF⊥AE，DF=AF=EF，
又∵∠ABC=90°，
∠DCF，∠AMF都与∠MAC互余，
∴∠DCF=∠AMF，
在△DFC和△AFM中，
，
∴△DFC≌△AFM（AAS），
∴CF=MF，
∴∠FMC=∠FCM；
（2）AD⊥MC，
理由：由（1）知，∠MFC=90°，FD=FA=FE，FM=FC，
∴∠FDE=∠FMC=45°，
∴DE∥CM，
∴AD⊥MC．
　
23．（2016?岑溪市一模）如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连结AE、DE、DC．www-2-1-cnjy-com
①求证：△ABE≌△CBD；
②若∠CAE=33°，求∠BDC的度数．
【解答】解：（1）∵∠ABC=90°，D为AB延长线上一点，
∴∠ABE=∠CBD=90°，
在△ABE和△CBD中，
，
∴△ABE≌△CBD（SAS）；
（2）∵AB=CB，∠ABC=90°，
∴△ABC为等腰直角三角形，
∴∠CAB=45°，
∵∠CAE=33°，
∴∠BAE=∠CAB﹣∠CAE=12°．
∵△ABE≌△CBD，
∴∠BCD=∠BAE=12°，
∴∠BDC=78°
答：∠BDC的度数为78°．
　
24． 已知：如图，△ABC中，∠ACB=45°，AD⊥BC于D，CF交AD于点F，连接BF并延长交AC于点E，∠BAD=∠FCD．
求证：（1）△ABD≌△CFD；
（2）BE⊥AC．
【解答】证明：（1）∵AD⊥BC，
∴∠ADC=∠FDB=90°．
∵∠ACB=45°，
∴∠ACB=∠DAC=45°，
∴AD=CD，
∵在△ABD和△CFD中，
，
∴△ABD≌△CFD（ASA），
（2）∵△ABD≌△CFD，
∴BD=FD，
∵∠FDB=90°，
∴∠FBD=∠BFD=45°，
∵∠ACB=45°，
∴∠BEC=90°，
∴BE⊥AC．
　

　
25． 如图，直线a、b相交于点A，C、E分别是直线b、a上两点且BC⊥a，DE⊥b，点M、N是EC、DB的中点．求证：MN⊥BD．21世纪教育网版权所有
【解答】证明：∵BC⊥a，DE⊥b，点M是EC的中点，
∴DM=EC，BM=EC，
∴DM=BM，
∵点N是BD的中点，
∴MN⊥BD．
　
26． 如图，在△ABC中，点D在AB上，且CD=CB，点E为BD的中点，点F为AC的中点，连结EF交CD于点M，连接AM．
（1）求证：EF=AC．
（2）若∠BAC=45°，求线段AM、DM、BC之间的数量关系．
【解答】（1）证明：∵CD=CB，点E为BD的中点，
∴CE⊥BD，
∵点F为AC的中点，
∴EF=AC；
（2）解：∵∠BAC=45°，CE⊥BD，
∴△AEC是等腰直角三角形，
∵点F为AC的中点，
∴EF垂直平分AC，
∴AM=CM，
∵CD=CM+DM=AM+DM，CD=CB，
∴BC=AM+DM．
　
27． 如图，在四边形ABCD中，∠BAD=∠BCD=90°，O为BD的中点，∠OAC和∠OCA相等吗？请说明理由．
【解答】解：∵△ABD是直角三角形，O为BD的中点，
∴OA=BD（直角三角形斜边中线等于斜边一半），
∵△BDC是直角三角形，O为BD的中点，
∴OC=BD，
∴OA=OC，
∴∠OAC=∠OCA．
　
28． 如图，△ABC中，AD是边BC上的高，CF是边AB上的中线，且DC=BF，DE⊥CF于E．
（1）E是CF的中点吗？试说明理由；
（2）试说明：∠B=2∠BCF．
【解答】（1）解：如图，连接DF，∵AD是边BC上的高，CF是边AB上的中线，
∴DF=BF=AB，
∵DC=BF，
∴CD=DF，
∵DE⊥CF，
∴E是CF的中点；
（2）证明：由（1）的结论DF=BF得∠FDB=∠FBD，
∵DC=BF，
∴∠DCF=∠DFC，
由外角的性质得∠FDB=∠DCF+∠DFC=2∠DCF，
∴∠FBD=2∠DCF，
即∠B=2∠BCF．
　
29．（2016春?深圳校级期中）如图，在△ACB中，∠ACB=90゜，CD⊥AB于D．
（1）求证：∠ACD=∠B；
（2）若AF平分∠CAB分别交CD、BC于E、F，求证：∠CEF=∠CFE．
【解答】证明：（1）∵∠ACB=90゜，CD⊥AB于D，
∴∠ACD+∠BCD=90°，∠B+∠BCD=90°，
∴∠ACD=∠B；
（2）在Rt△AFC中，∠CFA=90°﹣∠CAF，
同理在Rt△AED中，∠AED=90°﹣∠DAE．
又∵AF平分∠CAB，
∴∠CAF=∠DAE，
∴∠AED=∠CFE，
又∵∠CEF=∠AED，
∴∠CEF=∠CFE．