5.5平行四边形的判定(1)

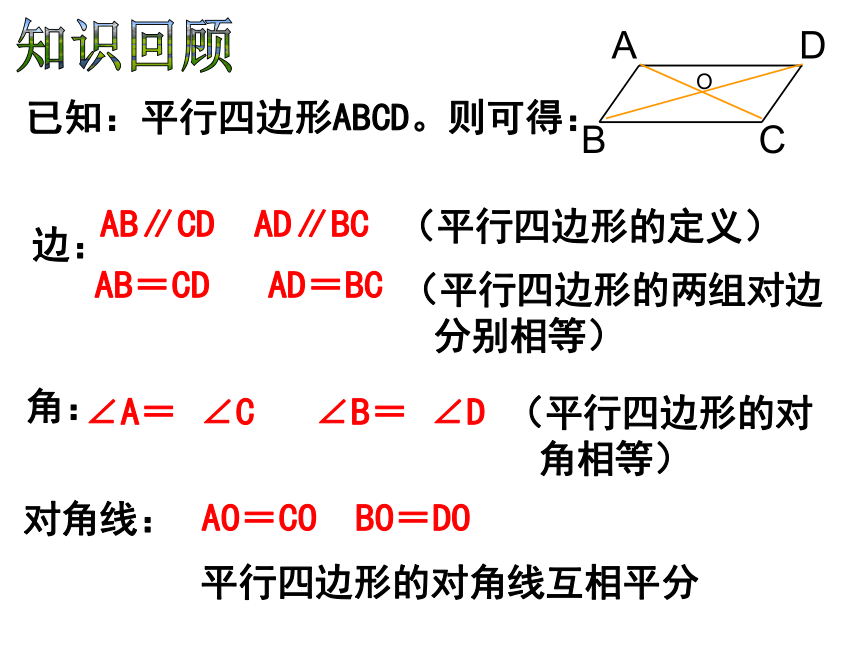
课件22张PPT。已知：平行四边形ABCD。则可得：边：角：对角线：AB＝CD　 AD＝BCAB∥CD　AD∥BC（平行四边形的两组对边
分别相等）（平行四边形的对
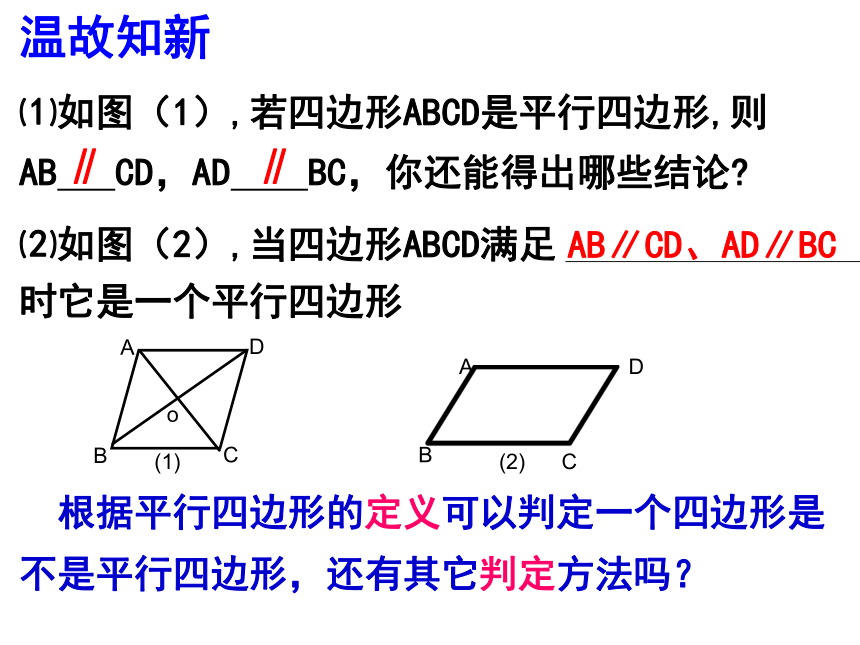
角相等）∠A＝ ∠C　 ∠B＝ ∠DAO＝CO　BO＝DO平行四边形的对角线互相平分知识回顾（平行四边形的定义）⑴如图（1）,若四边形ABCD是平行四边形,则
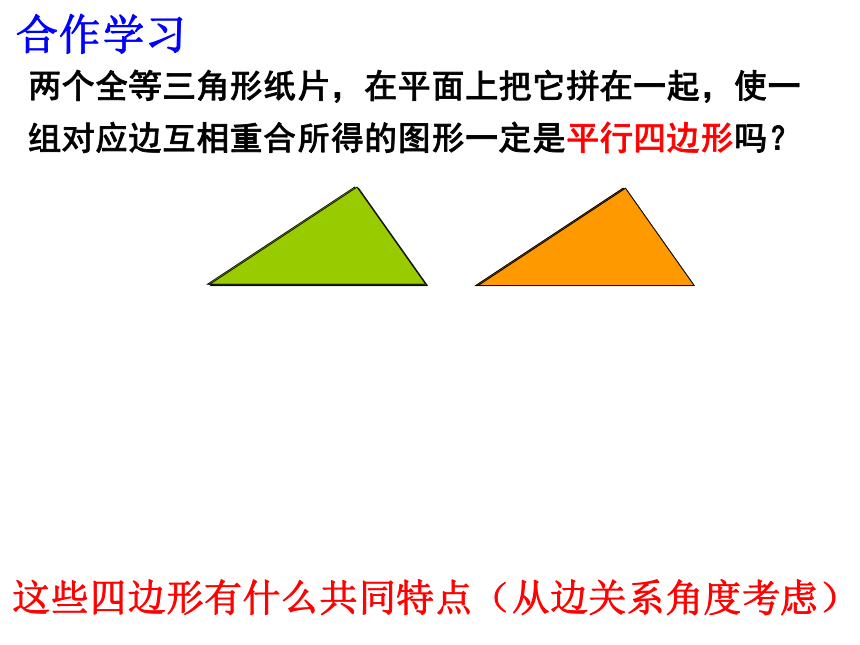
AB CD，AD BC，你还能得出哪些结论?∥∥AB∥CD、AD∥BC温故知新 根据平行四边形的定义可以判定一个四边形是不是平行四边形，还有其它判定方法吗？5.5平行四边形的判定（1）两个全等三角形纸片，在平面上把它拼在一起，使一
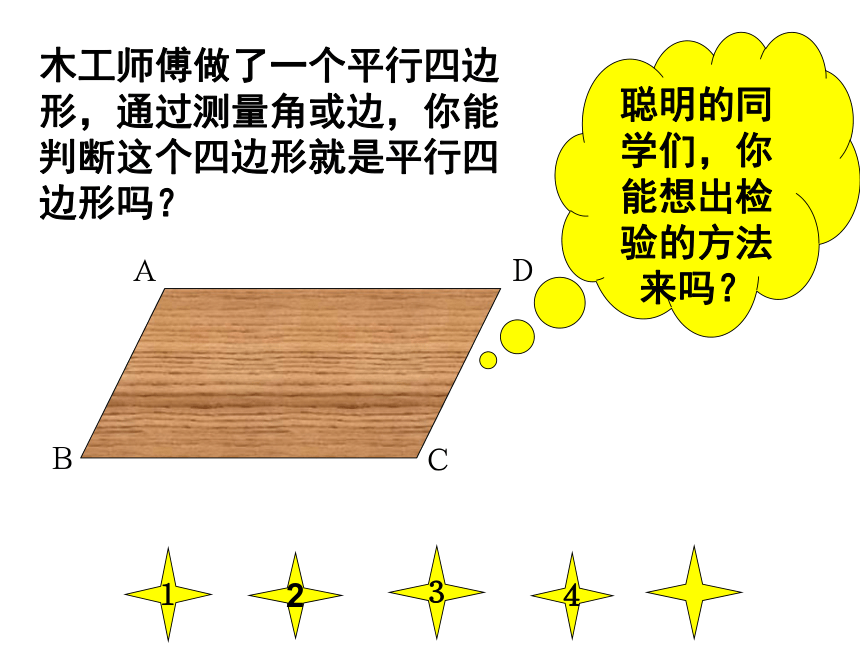
组对应边互相重合所得的图形一定是平行四边形吗？这些四边形有什么共同特点（从边关系角度考虑）合作学习木工师傅做了一个平行四边形，通过测量角或边，你能判断这个四边形就是平行四边形吗？ＡＤＢＣ１３４2聪明的同学们，你能想出检验的方法来吗？已知：在四边形ABCD中，
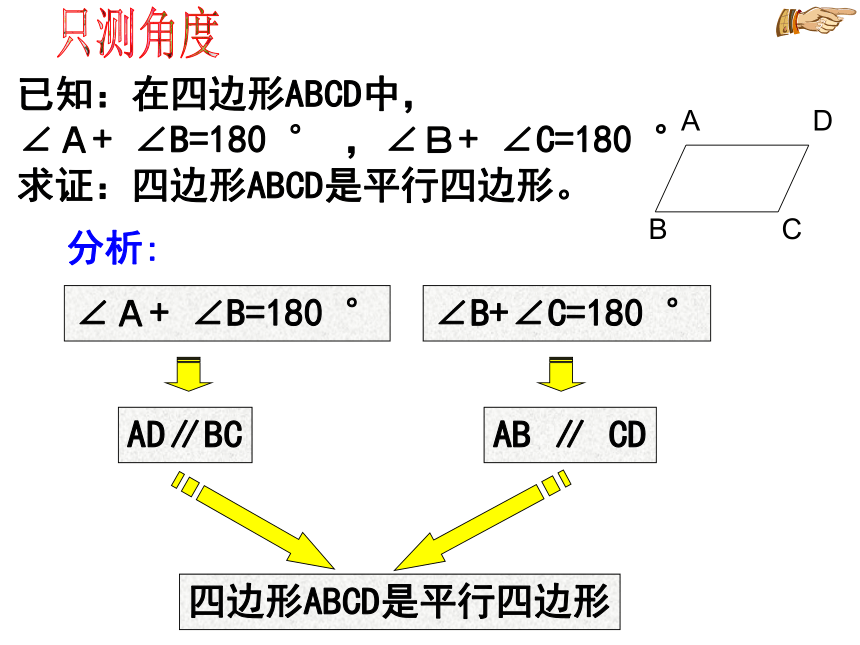
∠Ａ+ ∠B=180 ° ，∠Ｂ+ ∠C=180 °
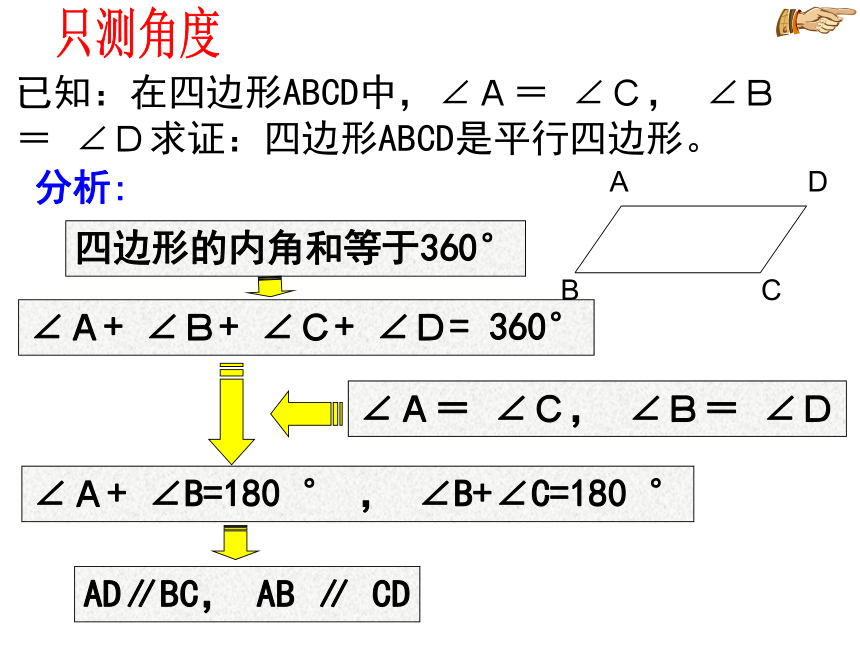
求证：四边形ABCD是平行四边形。只测角度分析:∠Ａ+ ∠B=180 °AB ∥ CD∠B+∠C=180 °AD∥BC四边形ABCD是平行四边形已知：在四边形ABCD中，∠Ａ＝ ∠Ｃ， ∠Ｂ＝ ∠Ｄ求证：四边形ABCD是平行四边形。分析:四边形的内角和等于360°∠Ａ+ ∠Ｂ+ ∠Ｃ+ ∠Ｄ= 360°∠Ａ+ ∠B=180 ° ， ∠B+∠C=180 °AD∥BC， AB ∥ CD只测角度已知：在四边形ABCD中，AB＝CD， AD＝BC ，
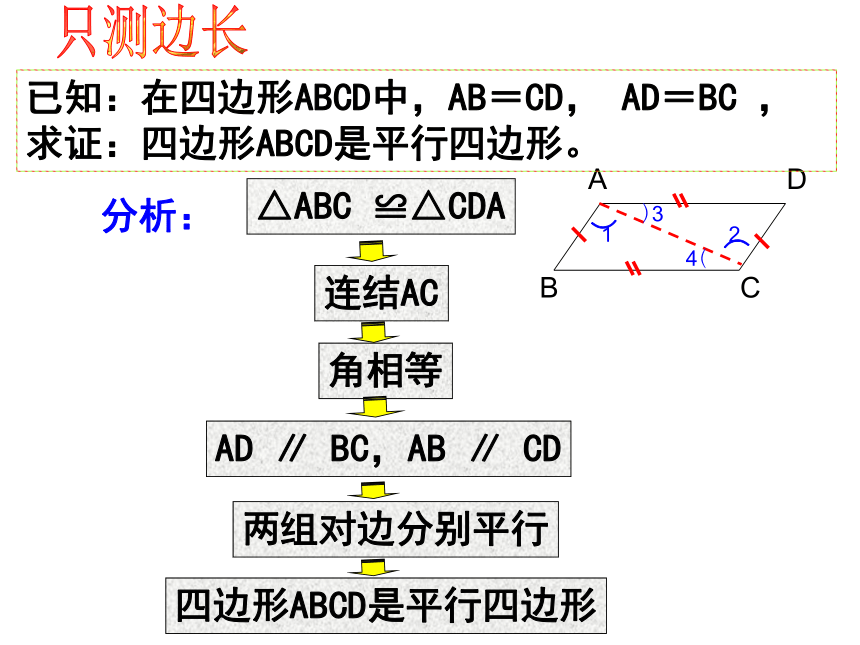
求证：四边形ABCD是平行四边形。只测边长分析：四边形ABCD是平行四边形两组对边分别平行AD ∥ BC，AB ∥ CD角相等连结AC△ABC ≌△CDA已知：在四边形ABCD中，AB＝CD， AD＝BC ，
求证：四边形ABCD是平行四边形。证明：连结AC。∴△ABC≌△CDA（SSS）∴ AB ∥ CD
　AD ∥ BC（内错角相等，两直线平行）∴四边形ABCD是平行四边形（平行四边形的定义）　∴∠1＝∠2
　∠3＝∠4（全等三角形的对应角相等）定理　两组对边分别相等的四边形是平行四边形只测边长已知：在四边形ABCD中，AB＝CD，AB ∥ CD，
求证：四边形ABCD是平行四边形。测一组对边平行且相等四边形ABCD是平行四边形两组对边分别平行AD ∥ BC且AB ∥ CD 角相等连结AC△ABC ≌△CDA已知：在四边形ABCD中，AB＝CD，AB ∥ CD，
求证：四边形ABCD是平行四边形。证明：连结AC。∵ AB ∥ CD （已知）
∴∠1＝∠2（两直线平行，内错角相等）又∵ AB＝CD（已知）
　　 AC＝CA（公共边）∴△ABC≌△CDA（SAS）∴∠3＝∠4（全等三角形的对应角相等）∴ AD ∥ BC（内错角相等，两直线平行）∴四边形ABCD是平行四边形（平行四边形的定义）定理1　一组对边平行且相等的四边形是平
行四边形测一组对边平行且相等只告诉木工师傅一组对边平行，另一组对边相等，是否一定做出平行四边形？疑问等腰梯形ABEDＤＡＢ平行四边形的判定方法两组对边
分别平行一组对边
平行且相等两组对边
分别相等平行四边形对边平行且相等对角相等对角线互相平分知识结构平行四边形的性质1.AB=CD，AB∥CD （ ）
2.AB=CD，AD=BC （ ）
3.AB=BC，AD=DC （ ）
4.AB ∥ CD，AD ∥ BC （ ）
5.AB ∥ CD，AD=BC （ ）
6.∠A+∠B=180°,AD=BC ( )满足下列条件的四边形ABCD是不是平行四边形，若是，在括号内打“√”，若不是，则打“×”。√√√××√判断例1、已知：如图，E,F分别是平行四边形ABCD 的边AD,BC的中点。求证：BE=DF.证明：∵四边形ABCD是平行四边形，∵E,F分别是AD,BC的中点，∴四边形EBFD是平行四边形∴BE=DF(一组对边平行且相等的四边形是平行四边形)(平行四边形的对边相等)∵四边形ABCD是平行四边形 ∴AB∥CDAB=CD
∵点E、F分别是边AB、CD的中点
∴AE∥DF 且AE=DF
∴ 四边形AEFD是平行四边形
∴ AD∥EF
∴EF//AD//BC 证明：（一组对边平行且相等的四边形是平行四边形）1、已知，四边形ABCD和AEFD都是平行四边形
求证：四边形BCFE是平行四边形证明：∵四边形ABCD是平行四边形
∴AD∥BC且 AD=BC ；
同理AD∥EF且AD=EF
∴ BC∥EF且BC=EF
∴四边形BCFE是平行四边形练一练2.已知，如图，AD⊥AC，BC⊥AC且AB=CD， 求证：AB∥CD.证明：∵ AD⊥AC，BC⊥AC
∴∠ACB=∠DAC=90o AD∥BC
∵AB=CD，AC=CA
∴Rt△ACB≌Rt△CAD
∴AD=BC
∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形）
∴ AB∥CD.（平行四边形的对边平行）例3、已知：E、F是平行四边形ABCD对角线AC上的两点，并且AE=CF。 求证：四边形BFDE是平行四边形∴AD∥BC且AD=BC∴△AED ≌ △CFB(SAS)∴ DE=BF∴ 四边形BFDE是平行四边形同理可证：BE=DF∵四边形ABCD是平行四边形证明：∵AE=FC∴∠EAD=∠FCB2、如图，在平行四边形ABCD中，E、F、G、H分别是各边上的点，且AE=CG，AH=CF，
求证：四边形EFGH是平行四边形。做一做请谈谈你在本节课中的收获