2.7勾股定理同步练习

2.7勾股定理同步练习
　
一．选择题（共12小题）
1．下列说法中，正确的有（　　）
①有一个角为60°的等腰三角形是等边三角形
②三边分别是1，，3的三角形是直角三角形
③一边上的中线等于这条边的一半的三角形是直角三角形
④三个角之比为3：4：5的三角形是直角三角形
A．1个 B．2个 C．3个 D．4个
2．（2016春?马山县校级月考）如图，已知长方形ABCD中，AD=6，AB=8，P是AD边上的点，将△ABP沿BP折叠，使点A落在点E上，PE、BE与CD分别交于点O、F，且OD=OE，则AP的长为（　　）【来源：21cnj*y.co*m】
A．4.8 B．5 C．5.2 D．5.4
3．（2016春?江汉区期中）如图，在Rt△ABC中，∠B=90°，AB=3cm，AC=5cm，将△ABC沿DE折叠，使点C与点A重合，则AE的长等于（　　）【版权所有：21教育】
A．4cm B．cm C．cm D．cm
4．（2016春?深圳校级期中）已知正方形ABCD的边长为3，E是BC上一点，BE=，Q是CD上一动点，将△CEQ沿直线EQ折叠后，点C落在点P处，连接PA，点Q从点C出发，沿线段CD向点D运动，当PA的长度最小时，CQ的长为（　　）
A．3﹣3 B．3﹣ C． D．3
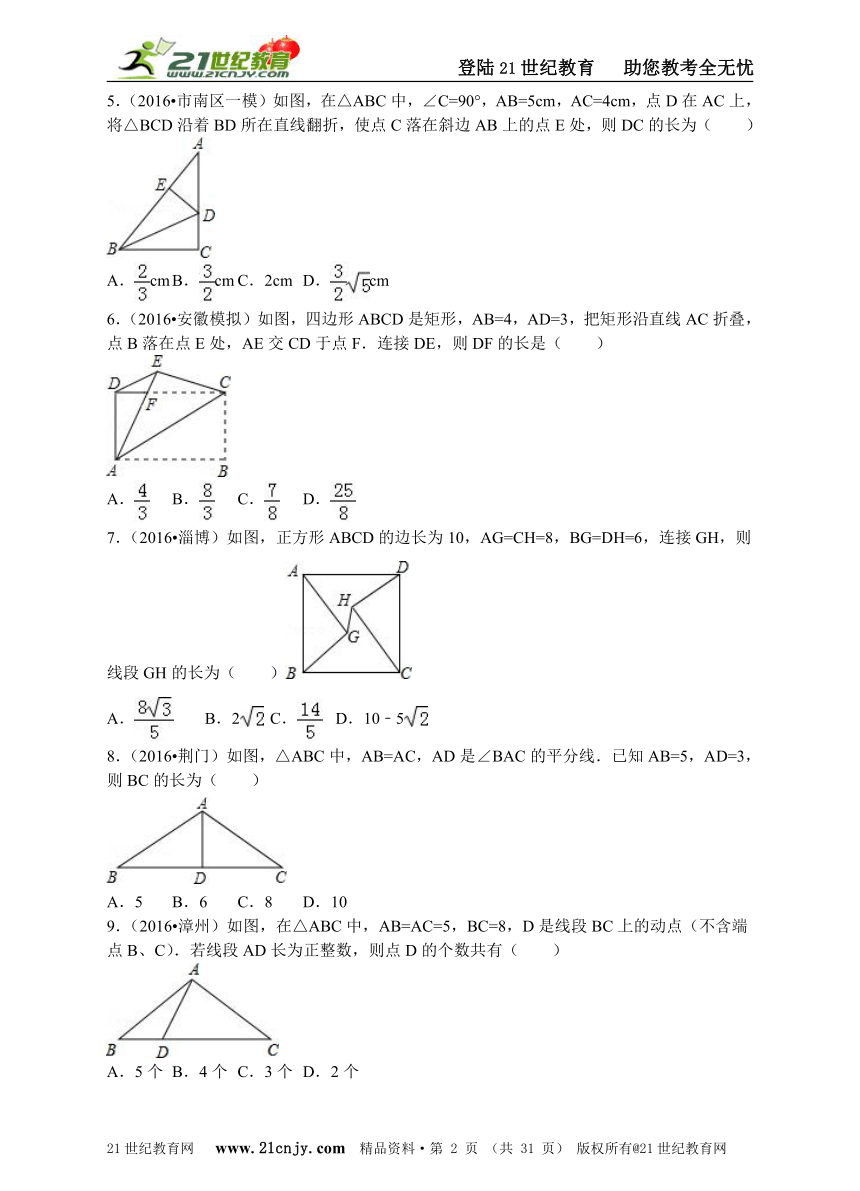
5．（2016?市南区一模）如图，在△ABC中，∠C=90°，AB=5cm，AC=4cm，点D在AC上，将△BCD沿着BD所在直线翻折，使点C落在斜边AB上的点E处，则DC的长为（　　）
A．cm B．cm C．2cm D．cm
6．（2016?安徽模拟）如图，四边形ABCD是矩形，AB=4，AD=3，把矩形沿直线AC折叠，点B落在点E处，AE交CD于点F．连接DE，则DF的长是（　　）
A． B． C． D．
7．（2016?淄博）如图，正方形ABCD的边长为10，AG=CH=8，BG=DH=6，连接GH，则线段GH的长为（　　）
A． B．2 C． D．10﹣5
8．（2016?荆门）如图，△ABC中，AB=AC，AD是∠BAC的平分线．已知AB=5，AD=3，则BC的长为（　　）
A．5 B．6 C．8 D．10
9．（2016?漳州）如图，在△ABC中，AB=AC=5，BC=8，D是线段BC上的动点（不含端点B、C）．若线段AD长为正整数，则点D的个数共有（　　）
A．5个 B．4个 C．3个 D．2个
10．（2016?株洲）如图，以直角三角形a、b、c为边，向外作等边三角形，半圆，等腰直角三角形和正方形，上述四种情况的面积关系满足S1+S2=S3图形个数有（　　）
A．1 B．2 C．3 D．4
11．（2016?青海）如图，正方形ABCD的边长为2，其面积标记为S1，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S2，…，按照此规律继续下去，则S9的值为（　　）21教育名师原创作品
A．（）6 B．（）7 C．（）6 D．（）7
12．（2016?黄冈校级自主招生）如图，四边形ABCD的对角线AC与BD互相垂直，若AB=3，BC=4，CD=5，则AD的长为（　　）
A．3 B．4 C．2 D．4
　
二．填空题（共6小题）
13．（2016?金华）如图，Rt△ABC纸片中，∠C=90°，AC=6，BC=8，点D在边BC 上，以AD为折痕△ABD折叠得到△AB′D，AB′与边BC交于点E．若△DEB′为直角三角形，则BD的长是______．21教育网
14．（2016?甘孜州）直角三角形斜边长是5，一直角边的长是3，则此直角三角形的面积为______．
15．（2016?烟台）如图，O为数轴原点，A，B两点分别对应﹣3，3，作腰长为4的等腰△ABC，连接OC，以O为圆心，CO长为半径画弧交数轴于点M，则点M对应的实数为______．
16．（2016?泰兴市二模）如图，△ABC中，AB=AC=10，BC=8，AD平分∠BAC交BC于点D，点E为AC的中点，连接DE，则△CDE的周长为______．
　
17．（2016?黄冈模拟）如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，点D在AB上，AD=AC，AF⊥CD交CD于点E，交CB于点F，则CF的长是______．
18．（2016?长春模拟）如图，在△ABC中，∠C=90°，AC=6，BC=8．以点A为圆心，AC长为半径作圆弧交边AB于点D，则BD的长为______．
三、解答题（共9小题）
　
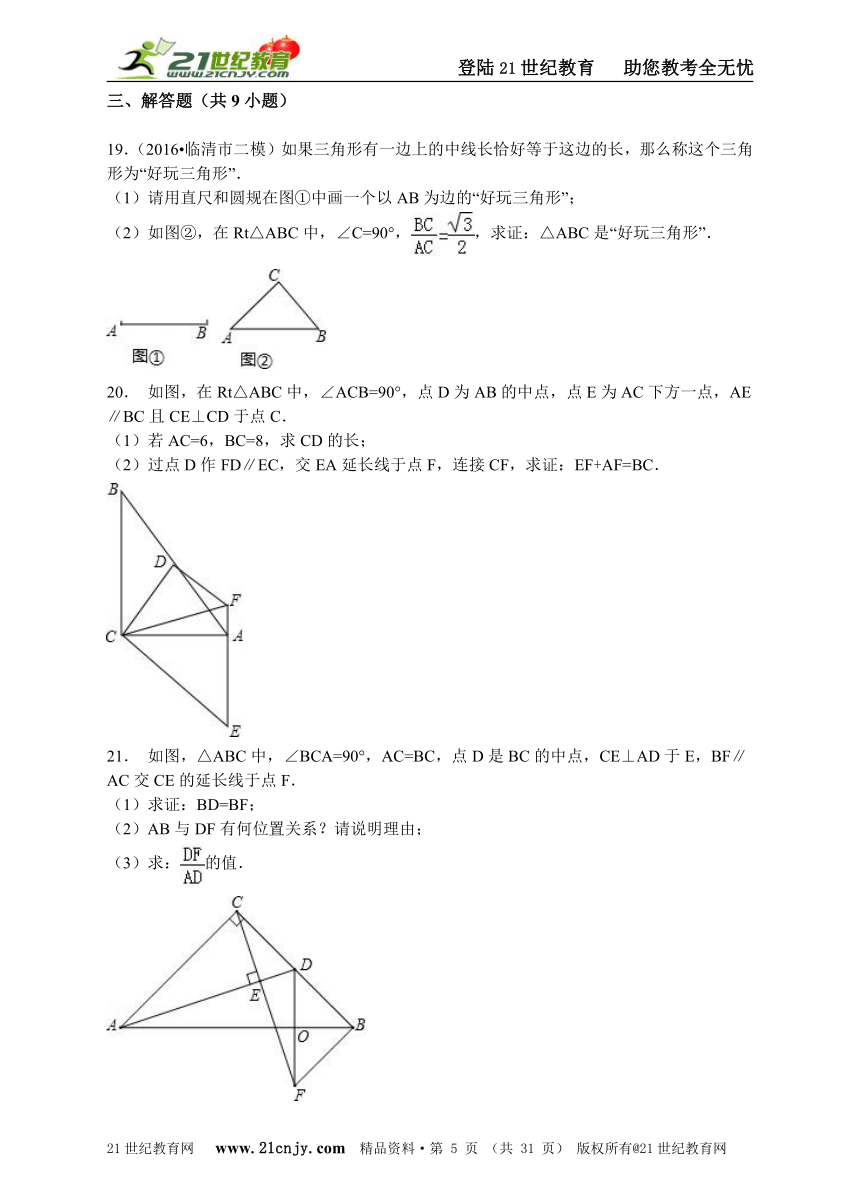
19．（2016?临清市二模）如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”．
（1）请用直尺和圆规在图①中画一个以AB为边的“好玩三角形”；
（2）如图②，在Rt△ABC中，∠C=90°，，求证：△ABC是“好玩三角形”．
20． 如图，在Rt△ABC中，∠ACB=90°，点D为AB的中点，点E为AC下方一点，AE∥BC且CE⊥CD于点C．
（1）若AC=6，BC=8，求CD的长；
（2）过点D作FD∥EC，交EA延长线于点F，连接CF，求证：EF+AF=BC．
21． 如图，△ABC中，∠BCA=90°，AC=BC，点D是BC的中点，CE⊥AD于E，BF∥AC交CE的延长线于点F．
（1）求证：BD=BF；
（2）AB与DF有何位置关系？请说明理由；
（3）求：的值．
22．如图所示，在等腰△ABC中，BC=AC，∠ACB=90°，D、E为斜边AB上的点，且∠DCE=45°【出处：21教育名师】
求证：DE2=AD2+BE2．
　
　
23．（2016?广东）如图，Rt△ABC中，∠B=30°，∠ACB=90°，CD⊥AB交AB于D，以CD为较短的直角边向△CDB的同侧作Rt△DEC，满足∠E=30°，∠DCE=90°，再用同样的方法作Rt△FGC，∠FCG=90°，继续用同样的方法作Rt△HIC，∠HCI=90°．若AC=a，求CI的长．
24．（2016?安徽模拟）定义：若三角形三个内角的度数分别是x、y和z，满足x2+y2=z2，则称这个三角形为勾股三角形．
（1）根据上述定义，“直角三角形是勾股三角形”是真命题还是假命题；
（2）已知一勾股三角形三个内角从小到大依次为x、y和z，且xy=2160，求x+y的值；
（3）如图，△ABC中，AB=，BC=2，AC=1+，求证：△ABC是勾股三角形．
25．（2016春?临清市期中）如图：四边形ABCD中，AB=CB=，CD=，DA=1，且AB⊥CB于B．
试求：（1）∠BAD的度数；
（2）四边形ABCD的面积．
26．（2016春?孝南区校级月考）已知，如图，在四边形ABCD中，∠ABC=90°，CD⊥AD，AD2+CD2=2AB2，求证：AB=BC．
27． 已知△ABC中，AB=AC．
（1）如图1，在△ADE中，若AD=AE，且∠DAE=∠BAC，求证：CD=BE；
（2）如图2，在△ADE中，若∠DAE=∠BAC=60°，且CD垂直平分AE，AD=3，CD=4，求BD的长；
（3）如图3，在△ADE中，当BD垂直平分AE于H，且∠BAC=2∠ADB时，试探究CD2，BD2，AH2之间的数量关系，并证明．
　

2.7勾股定理同步练习
参考答案与试题解析
　
一．选择题（共12小题）
1． 下列说法中，正确的有（　　）
①有一个角为60°的等腰三角形是等边三角形
②三边分别是1，，3的三角形是直角三角形
③一边上的中线等于这条边的一半的三角形是直角三角形
④三个角之比为3：4：5的三角形是直角三角形
A．1个 B．2个 C．3个 D．4个
【分析】分别根据等边三角形及直角三角形的判定定理解答．
【解答】解：①正确，符合等边三角形的判定定理；
②正确，因为12+32=（）2，所以三边分别是1，，3的三角形是直角三角形；
③正确，根据矩形对角线的性质的逆命题；
④错误，三边之比为3：4：5的三角形是直角三角形．
故选C．
【点评】本题考查的是等边三角形及直角三角形的判定定理，比较简单．
　
2．（2016春?马山县校级月考）如图，已知长方形ABCD中，AD=6，AB=8，P是AD边上的点，将△ABP沿BP折叠，使点A落在点E上，PE、BE与CD分别交于点O、F，且OD=OE，则AP的长为（　　）
A．4.8 B．5 C．5.2 D．5.4
【分析】由矩形的性质得出∠A=∠C=∠D=90°，CD=AB=8，BC=AD=6，由折叠的性质得出EP=AP，BE=AB=8，∠E=∠A=90°，由ASA证明△ODP≌△OEF，得出PD=FE，OP=OF，因此DF=EP=AP，设AP=x，则DF=x，FE=PD=6﹣x，得出CF=CD﹣DF=8﹣x，BF=BE﹣FE=x+2，在Rt△BCF中，由勾股定理得出方程，解方程即可．
【解答】解：∵四边形ABCD是长方形，
∴∠A=∠C=∠D=90°，CD=AB=8，BC=AD=6，
由折叠的性质得：EP=AP，BE=AB=8，∠E=∠A=90°，
在△ODP和△OEF中，，
∴△ODP≌△OEF（ASA），
∴PD=FE，OP=OF，
∴DF=EP=AP，
设AP=x，则DF=x，FE=PD=6﹣x，
∴CF=CD﹣DF=8﹣x，BF=BE﹣FE=x+2，
在Rt△BCF中，BC2+CF2=BF2，
即62+（8﹣x）2=（x+2）2，
解得：x=4.8；
故选：A．
【点评】本题考查了矩形的性质、折叠的性质、勾股定理、全等三角形的判定与性质；熟练掌握矩形和折叠的性质，证明三角形全等进一步得出DF=EP是解决问题的关键．
　
3．（2016春?江汉区期中）如图，在Rt△ABC中，∠B=90°，AB=3cm，AC=5cm，将△ABC沿DE折叠，使点C与点A重合，则AE的长等于（　　）21·cn·jy·com
A．4cm B．cm C．cm D．cm
【分析】设AE=xcm，根据勾股定理求出BC，用x表示出BE，根据勾股定理列出方程，解方程即可．
【解答】解：设AE=xcm，由翻折变换的性质可知，EC=xcm，
∵∠B=90°，AB=3cm，AC=5cm，
∴BC==4cm，
∴BE=BC﹣CE=（4﹣x）cm，
在Rt△ABE中，AE2=AB2+BE2，即x2=32+（4﹣x）2，
解得，x=，
故选：C．
【点评】本题考查的是翻折变换的性质和勾股定理的应用，翻折变换是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
　
4．（2016春?深圳校级期中）已知正方形ABCD的边长为3，E是BC上一点，BE=，Q是CD上一动点，将△CEQ沿直线EQ折叠后，点C落在点P处，连接PA，点Q从点C出发，沿线段CD向点D运动，当PA的长度最小时，CQ的长为（　　）
A．3﹣3 B．3﹣ C． D．3
【分析】先求得AE和CE的长，然后由翻折的性质得到PE=EC，最后根据当点A、P、E一条直线上时，AP有最小值求解即可．2·1·c·n·j·y
【解答】解：如图所示：
在Rt△ABE中，AE===2．
∵BC=3，BE=，
∴EC=3﹣．
由翻折的性质可知：PE=CE=3﹣．
∵AP+PE≥AE，
∴AP≥AE﹣PE．
∴当点A、P、E一条直线上时，AP有最小值．
∴AP=AE﹣PE=2﹣（3﹣）=3﹣3．
故选：A．
【点评】本题主要考查的是翻折的性质、勾股定理的应用，明确当点A、P、E在一条直线上时，AP有最小值是解题的关键．【来源：21·世纪·教育·网】
　
5．（2016?市南区一模）如图，在△ABC中，∠C=90°，AB=5cm，AC=4cm，点D在AC上，将△BCD沿着BD所在直线翻折，使点C落在斜边AB上的点E处，则DC的长为（　　）
A．cm B．cm C．2cm D．cm
【分析】首先由勾股定理求出BC，由折叠的性质可得∠BED=∠C=90°，BE=BC=3cm，得出AE=AB﹣BE=2cm，设DC=xcm，则DE=xcm，AD=（4﹣x）cm，由勾股定理得出方程，解方程即可．
【解答】解：∵∠C=90°，AB=5cm，AC=4cm，
∴BC==3cm，
∵将△BCD沿着直线BD翻折，使点C落在斜边AB上的点E处，
∴△BED≌△BCD，
∴∠BED=∠C=90°，BE=BC=3cm，
∴AE=AB﹣BE=2cm，
设DC=xcm，则DE=xcm，AD=（4﹣x）cm，
由勾股定理得：AE2+DE2=AD2，
即22+x2=（4﹣x）2，
解得：x=．
故选：B．
【点评】本题主要考查翻折变换的性质，全等三角形的性质，勾股定理；熟练掌握翻折变换的性质，由勾股定理得出方程是解决问题的关键．21世纪教育网版权所有
　
6．（2016?安徽模拟）如图，四边形ABCD是矩形，AB=4，AD=3，把矩形沿直线AC折叠，点B落在点E处，AE交CD于点F．连接DE，则DF的长是（　　）
A． B． C． D．
【分析】由四边形ABCD是矩形与△AEC由△ABC翻折得到，AD=CE，∠ADF=∠CEF，由AAS证得△ADF≌△CEF，的长FA=FC，设DF=x，则FA=4﹣x，由勾股定理得：DA2+DF2=AF2，即可求出DF的长．
【解答】解：∵四边形ABCD是矩形，
∴AD=BC，AB=DC=4，∠ADF=90°，∵△AEC由△ABC翻折得到，
∴BC=EC，∠CEF=∠ABC=90°，
∴AD=CE，∠ADF=∠CEF，
在△ADF与△CEF中，
，
∴△ADF≌△CEF（AAS），
∴FA=FC，
设DF=x，则FA=FC=DC﹣DF=4﹣x，
在Rt△DFA中，由勾股定理得：DA2+DF2=AF2，
即32+x2=（4﹣x）2，
解得：x=，
即DF的长是．
故选C．
【点评】本题主要考查了折叠的性质、矩形的性质、全等三角形的判定与性质、勾股定理等知识；熟练掌握折叠的性质，得到相等的线段与角是解决问题的关键．
　
7．（2016?淄博）如图，正方形ABCD的边长为10，AG=CH=8，BG=DH=6，连接GH，则线段GH的长为（　　）
A． B．2 C． D．10﹣5
【分析】延长BG交CH于点E，根据正方形的性质证明△ABG≌△CDH≌△BCE，可得GE=BE﹣BG=2、HE=CH﹣CE=2、∠HEG=90°，由勾股定理可得GH的长．
【解答】解：如图，延长BG交CH于点E，
在△ABG和△CDH中，
，
∴△ABG≌△CDH（SSS），
AG2+BG2=AB2，
∴∠1=∠5，∠2=∠6，∠AGB=∠CHD=90°，
∴∠1+∠2=90°，∠5+∠6=90°，
又∵∠2+∠3=90°，∠4+∠5=90°，
∴∠1=∠3=∠5，∠2=∠4=∠6，
在△ABG和△BCE中，
，
∴△ABG≌△BCE（ASA），
∴BE=AG=8，CE=BG=6，∠BEC=∠AGB=90°，
∴GE=BE﹣BG=8﹣6=2，
同理可得HE=2，
在RT△GHE中，GH===2，
故选：B．
【点评】本题主要考查正方形的性质、全等三角形的判定与性质、勾股定理及其逆定理的综合运用，通过证三角形全等得出△GHE为等腰直角三角形是解题的关键．
　
8．（2016?荆门）如图，△ABC中，AB=AC，AD是∠BAC的平分线．已知AB=5，AD=3，则BC的长为（　　）21*cnjy*com
A．5 B．6 C．8 D．10
【分析】根据等腰三角形的性质得到AD⊥BC，BD=CD，根据勾股定理即可得到结论．
【解答】解：∵AB=AC，AD是∠BAC的平分线，
∴AD⊥BC，BD=CD，
∵AB=5，AD=3，
∴BD==4，
∴BC=2BD=8，
故选C．
【点评】本题考查了勾股定理，等腰三角形的性质，熟练掌握等腰三角形的性质是解题的关键．
　
9．（2016?漳州）如图，在△ABC中，AB=AC=5，BC=8，D是线段BC上的动点（不含端点B、C）．若线段AD长为正整数，则点D的个数共有（　　）
A．5个 B．4个 C．3个 D．2个
【分析】首先过A作AE⊥BC，当D与E重合时，AD最短，首先利用等腰三角形的性质可得BE=EC，进而可得BE的长，利用勾股定理计算出AE长，然后可得AD的取值范围，进而可得答案．
【解答】解：过A作AE⊥BC，
∵AB=AC，
∴EC=BE=BC=4，
∴AE==3，
∵D是线段BC上的动点（不含端点B、C）．
∴3≤AD＜5，
∴AD=3或4，
∵线段AD长为正整数，
∴点D的个数共有3个，
故选：C．
【点评】此题主要考查了等腰三角形的性质和勾股定理，关键是正确利用勾股定理计算出AD的最小值，然后求出AD的取值范围．
　
10．（2016?株洲）如图，以直角三角形a、b、c为边，向外作等边三角形，半圆，等腰直角三角形和正方形，上述四种情况的面积关系满足S1+S2=S3图形个数有（　　）
A．1 B．2 C．3 D．4
【分析】根据直角三角形a、b、c为边，应用勾股定理，可得a2+b2=c2．
（1）第一个图形中，首先根据等边三角形的面积的求法，表示出3个三角形的面积；然后根据a2+b2=c2，可得S1+S2=S3．
（2）第二个图形中，首先根据圆的面积的求法，表示出3个半圆的面积；然后根据a2+b2=c2，可得S1+S2=S3．
（3）第三个图形中，首先根据等腰直角三角形的面积的求法，表示出3个等腰直角三角形的面积；然后根据a2+b2=c2，可得S1+S2=S3．
（4）第四个图形中，首先根据正方形的面积的求法，表示出3个正方形的面积；然后根据a2+b2=c2，可得S1+S2=S3．
【解答】解：（1）S1=a2，S2=b2，S3=c2，
∵a2+b2=c2，
∴a2+b2=c2，
∴S1+S2=S3．
（2）S1=a2，S2=b2，S3=c2，
∵a2+b2=c2，
∴a2+b2=c2，
∴S1+S2=S3．
（3）S1=a2，S2=b2，S3=c2，
∵a2+b2=c2，
∴a2+b2=c2，
∴S1+S2=S3．
（4）S1=a2，S2=b2，S3=c2，
∵a2+b2=c2，
∴S1+S2=S3．
综上，可得
面积关系满足S1+S2=S3图形有4个．
故选：D．
【点评】（1）此题主要考查了勾股定理的应用，要熟练掌握，解答此题的关键是要明确：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
（2）此题还考查了等腰直角三角形、等边三角形、圆以及正方形的面积的求法，要熟练掌握．
　
11．（2016?青海）如图，正方形ABCD的边长为2，其面积标记为S1，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S2，…，按照此规律继续下去，则S9的值为（　　）
A．（）6 B．（）7 C．（）6 D．（）7
【分析】根据等腰直角三角形的性质可得出S2+S2=S1，写出部分Sn的值，根据数的变化找出变化规律“Sn=（）n﹣3”，依此规律即可得出结论．
【解答】解：在图中标上字母E，如图所示．
∵正方形ABCD的边长为2，△CDE为等腰直角三角形，
∴DE2+CE2=CD2，DE=CE，
∴S2+S2=S1．
观察，发现规律：S1=22=4，S2=S1=2，S3=S2=1，S4=S3=，…，
∴Sn=（）n﹣3．
当n=9时，S9=（）9﹣3=（）6，
故选：A．
【点评】本题考查了等腰直角三角形的性质、勾股定理以及规律型中数的变化规律，解题的关键是找出规律“Sn=（）n﹣3”．本题属于中档题，难度不大，解决该题型题目时，写出部分Sn的值，根据数值的变化找出变化规律是关键．　　21*cnjy*com
　
12．（2016?黄冈校级自主招生）如图，四边形ABCD的对角线AC与BD互相垂直，若AB=3，BC=4，CD=5，则AD的长为（　　）
A．3 B．4 C．2 D．4
【分析】在Rt△AOB、Rt△DOC中分别表示出AO2、DO2，从而在Rt△ADO中利用勾股定理即可得出AD的长度．
【解答】解：在Rt△AOB中，AO2=AB2﹣BO2；
Rt△DOC中可得：DO2=DC2﹣CO2；
∴可得AD2=AO2+DO2=AB2﹣BO2+DC2﹣CO2=18，
即可得AD==3．
故选A．
【点评】此题考查了勾股定理的知识，解答本题的关键是在Rt△AOB、Rt△DOC中分别表示出AO2、DO2，需要我们熟练掌握勾股定理的表达形式．
　
二．填空题（共6小题）
13．（2016?金华）如图，Rt△ABC纸片中，∠C=90°，AC=6，BC=8，点D在边BC 上，以AD为折痕△ABD折叠得到△AB′D，AB′与边BC交于点E．若△DEB′为直角三角形，则BD的长是　2或5　．
14．（2016?甘孜州）直角三角形斜边长是5，一直角边的长是3，则此直角三角形的面积为　6　．
【分析】根据直角三角形的斜边与一条直角边，可利用勾股定理求出另一条直角边的长度，再根据三角形的面积公式求出面积即可．
【解答】解：∵直角三角形斜边长是5，一直角边的长是3，
∴另一直角边长为=4．
该直角三角形的面积S=×3×4=6．
故答案为：6．
【点评】本题考查了勾股定理以及三角形的面积公式，解题的关键是根据勾股定理求出另一条直角边的长度．本题属于基础题，难度不大，解决该题型题目时，根据勾股定理找出直角三角形的三边关系是关键．
　
　
15．（2016?烟台）如图，O为数轴原点，A，B两点分别对应﹣3，3，作腰长为4的等腰△ABC，连接OC，以O为圆心，CO长为半径画弧交数轴于点M，则点M对应的实数为　　．
【分析】先利用等腰三角形的性质得到OC⊥AB，则利用勾股定理可计算出OC=，然后利用画法可得到OM=OC=，于是可确定点M对应的数．
【解答】解：∵△ABC为等腰三角形，OA=OB=3，
∴OC⊥AB，
在Rt△OBC中，OC===，
∵以O为圆心，CO长为半径画弧交数轴于点M，
∴OM=OC=，
∴点M对应的数为．
故答案为．
【点评】本题考查了勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．也考查了等腰三角形的性质．
　
16．（2016?泰兴市二模）如图，△ABC中，AB=AC=10，BC=8，AD平分∠BAC交BC于点D，点E为AC的中点，连接DE，则△CDE的周长为　14　．
【分析】根据等腰三角形三线合一的性质可得AD⊥BC，CD=BD，再根据直角三角形斜边上的中线等于斜边的一半可得DE=CE=AC，然后根据三角形的周长公式列式计算即可得解．
【解答】解：∵AB=AC，AD平分∠BAC，BC=8，
∴AD⊥BC，CD=BD=BC=4，
∵点E为AC的中点，
∴DE=CE=AC=5，
∴△CDE的周长=CD+DE+CE=4+5+5=14．
故答案为14．
【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质，等腰三角形三线合一的性质，熟记性质并准确识图是解题的关键．
　
17．（2016?黄冈模拟）如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，点D在AB上，AD=AC，AF⊥CD交CD于点E，交CB于点F，则CF的长是　1.5　．
【分析】连接DF，由勾股定理求出AB=5，由等腰三角形的性质得出CE=DE，由线段垂直平分线的性质得出CF=DF，由SSS证明△ADF≌△ACF，得出∠ADF=∠ACF=∠BDF=90°，设CF=DF=x，则BF=4﹣x，在Rt△BDF中，由勾股定理得出方程，解方程即可．
【解答】解：连接DF，如图所示：
∵在Rt△ABC中，∠ACB=90°，AC=3，BC=4，
∴AB==5，
∵AD=AC=3，AF⊥CD，
∴CE=DE，BD=AB﹣AD=2，
∴CF=DF，
在△ADF和△ACF中，，
∴△ADF≌△ACF（SSS），
∴∠ADF=∠ACF=90°，
∴∠BDF=90°，
设CF=DF=x，则BF=4﹣x，
在Rt△BDF中，由勾股定理得：DF2+BD2=BF2，
即x2+22=（4﹣x）2，
解得：x=1.5；
∴CF=1.5；
故答案为：1.5．
【点评】本题考查了勾股定理、全等三角形的判定与性质、等腰三角形的性质、线段垂直平分线的性质；熟练掌握勾股定理，证明三角形全等是解决问题的关键．
　
　
18．（2016?长春模拟）如图，在△ABC中，∠C=90°，AC=6，BC=8．以点A为圆心，AC长为半径作圆弧交边AB于点D，则BD的长为　4　．
【分析】首先利用勾股定理可以算出AB的长，再根据题意可得到AD=AC，根据BD=AB﹣AD即可算出答案．
【解答】解：∵AC=6，BC=8，
∴AB==10，
∵以点A为圆心，AC长为半径画弧，交AB于点D，
∴AD=AC，
∴AD=6，
∴BD=AB﹣AD=10﹣6=4．
故答案为：4．
【点评】此题主要考查了勾股定理，关键是熟练掌握勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
【分析】先依据勾股定理求得AB的长，然后由翻折的性质可知：AB′=10，DB=DB′，接下来分为∠B′DE=90°和∠B′ED=90°，两种情况画出图形，设DB=DB′=x，然后依据勾股定理列出关于x的方程求解即可．
【解答】解：∵Rt△ABC纸片中，∠C=90°，AC=6，BC=8，
∴AB=10，
∵以AD为折痕△ABD折叠得到△AB′D，
∴BD=DB′，AB′=AB=10．
如图1所示：当∠B′DE=90°时，过点B′作B′F⊥AF，垂足为F．
设BD=DB′=x，则AF=6+x，FB′=8﹣x．
在Rt△AFB′中，由勾股定理得：AB′2=AF2+FB′2，即（6+x）2+（8﹣x）2=102．
解得：x1=2，x2=0（舍去）．
∴BD=2．
如图2所示：当∠B′ED=90°时，C与点E重合．
∵AB′=10，AC=6，
∴B′E=4．
设BD=DB′=x，则CD=8﹣x．
在Rt△′BDE中，DB′2=DE2+B′E2，即x2=（8﹣x）2+42．
解得：x=5．
∴BD=5．
综上所述，BD的长为2或5．
故答案为：2或5．
【点评】本题主要考查的是翻折的性质、勾股定理的应用，根据勾股定理列出关于x的方程是解题的关键．
　
三、解答题（共9小题）　
19．（2016?临清市二模）如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”．21cnjy.com
（1）请用直尺和圆规在图①中画一个以AB为边的“好玩三角形”；
（2）如图②，在Rt△ABC中，∠C=90°，，求证：△ABC是“好玩三角形”．
【分析】（1）先作AB的垂直平分线得到AB的中点D，然后以D为端点任意画线段CD=AB，再连结AC、BC，则△ACB满足条件；www-2-1-cnjy-com
（2）取AC的中点D，连结BD，如图②，设AC=2x，则CD=AD=x，利用得到BC=x，再在Rt△BCD中利用勾股定理计算出BD=2x，则BD=AC，然后根据“好玩三角形”即可得到结论．
【解答】（1）解：如图①，△ABC为所作；
（2）证明：取AC的中点D，连结BD，如图②，
设AC=2x，则CD=AD=x，
∵，
∴BC=x，
在Rt△BCD中，BD===2x，
∴BD=AC，
∴△ABC是“好玩三角形”．
【点评】本题考查了作图﹣复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．
　
20． 如图，在Rt△ABC中，∠ACB=90°，点D为AB的中点，点E为AC下方一点，AE∥BC且CE⊥CD于点C．
（1）若AC=6，BC=8，求CD的长；
（2）过点D作FD∥EC，交EA延长线于点F，连接CF，求证：EF+AF=BC．
【分析】（1）根据勾股定理可求得AB的长，再根据直角三角形斜边中线是斜边一半可以求得CD的长；
（2）延长FD交BC于点G，易证△ADF≌△BDG和△CFG≌△FCA，可得AF=BG和EF=CG即可解题．
【解答】解：（1）∵Rt△ABC中，∠ACB=90°，AC=6，BC=8，
∴AB==10，
∵点D为AB的中点，
∴CD=AB=5；
（2）延长FD交BC于点G，
∵EF∥BC，
∴∠FAD=∠GBD，
在△ADF和△BDG中，
，
∴△ADF≌△BDG，（ASA）
∴AF=BG，
∵EF∥BC，DF∥CE，
∴∠CFE=∠BCF，∠CFD=∠FCE，
在△CFG和△FCA中，
，
∴△CFG≌△FCE（ASA），
∴EF=CG，
∵BC=BG+CG，
∴BC=EF+AF．
【点评】本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，考查了斜边中线是斜边一半的性质，本题中求证△ADF≌△BDG和△CFG≌△FCA是解题的关键．
　
21． 如图，△ABC中，∠BCA=90°，AC=BC，点D是BC的中点，CE⊥AD于E，BF∥AC交CE的延长线于点F．
（1）求证：BD=BF；
（2）AB与DF有何位置关系？请说明理由；
（3）求：的值．
【分析】（1）求出∠CAD=∠BCF，∠CBF=∠ACD，证△ACD≌△CBF，推出CD=BF即可；
（2）求出∠CBA=∠FBA，根据等腰三角形的性质得出即可；
（3）设CD=BD=BF=x，得出AC=BC=2x，根据勾股定理求出AD、DF，即可得出答案．
【解答】（1）证明：∵∠ACD=90°，CE⊥AD，
∴∠CED=90°，
∴∠CAD+∠CDA=90°，∠CDE+∠BCF=90°，
∴∠CAD=∠BCF，
∵BF∥AC，∠ACB=90°，
∴∠CBF=90°=∠ACD，
在△ACD和△CBF中
∴△ACD≌△CBF，
∴CD=BF，
∵D为BC的中点，
∴CD=BD，
∴BD=BF；
（2）解：AB垂直平分DF，
理由是：∵∠ACB=90°，AC=BC，
∴∠CBA=∠CAB=45°，
∵∠CBF=90°，
∴∠FBA=45°=∠CBA，
∵BD=BF，
∴AB垂直平分DF；
（3）解：设CD=BD=BF=x，
则AC=BC=2x，
在Rt△ACD中，由勾股定理得：AD==x，
在Rt△DBF中，由勾股定理得：DF==x，
则==．
【点评】本题考查了勾股定理，全等三角形的性质和判定，等腰直角三角形，等腰三角形性质的应用，主要考查了学生的推理能力，综合性比较强，有一定的难度．
　
22．如图所示，在等腰△ABC中，BC=AC，∠ACB=90°，D、E为斜边AB上的点，且∠DCE=45°21·世纪*教育网
求证：DE2=AD2+BE2．
【分析】如图，将△ADC绕点C逆时针旋转90°到△CBF的位置；证明∠A=∠ABC=∠CBF=45°，得到EF2=AD2+BE2
证明△DCE≌△FCE，得到DE=EF，故DE2=AD2+BE2．
【解答】证明：如图，将△ADC绕点C逆时针旋转90°到△CBF的位置；
则CD=CE，AD=BF；∠BCF=∠ACD，∠CBF=∠A；
∵BC=AC，∠ACB=90°，
∴∠A=∠ABC=∠CBF=45°，
∴∠EBF=90°，EF2=BE2+BF2=AD2+BE2；
∵∠DCE=45°，∠ACB=90°，
∴∠ACD+∠BCE=90°﹣45°=45°，而∠ACD=∠BCF，
∴∠ECF=∠ECD=45°；在△DCE与△FCE中，
，
∴△DCE≌△FCE（SAS），
∴DE=EF，
∴DE2=AD2+BE2．
【点评】该题主要考查了旋转变换的性质、全等三角形的判定及其性质、勾股定理等几何知识点及其应用问题；解题的关键是作旋转变换，将分散的条件集中到某个三角形中．
　
　
23．（2016?广东）如图，Rt△ABC中，∠B=30°，∠ACB=90°，CD⊥AB交AB于D，以CD为较短的直角边向△CDB的同侧作Rt△DEC，满足∠E=30°，∠DCE=90°，再用同样的方法作Rt△FGC，∠FCG=90°，继续用同样的方法作Rt△HIC，∠HCI=90°．若AC=a，求CI的长．
【分析】在Rt△ACD中，利用30度角的性质和勾股定理求CD的长；同理在Rt△ECD中求FC的长，在Rt△FCG中求CH的长；最后在Rt△HCI中，利用30度角的性质和勾股定理求CI的长．
【解答】解：在Rt△ACB中，∠B=30°，∠ACB=90°，
∴∠A=90°﹣30°=60°，
∵CD⊥AB，
∴∠ADC=90°，
∴∠ACD=30°，
在Rt△ACD中，AC=a，
∴AD=a，
由勾股定理得：CD==，
同理得：FC=×=，CH=×=，
在Rt△HCI中，∠I=30°，
∴HI=2HC=，
由勾股定理得：CI==，
答：CI的长为．
【点评】本题考查了勾股定理和直角三角形含30°角的性质，在直角三角形中，30°角所对的直角边等于斜边的一半，这一性质经常运用，必须熟练掌握；同时在运用勾股定理和直角三角形含30°角的性质时，一定要书写好所在的直角三角形，尤其是此题多次运用了这一性质．
　
24．（2016?安徽模拟）定义：若三角形三个内角的度数分别是x、y和z，满足x2+y2=z2，则称这个三角形为勾股三角形．
（1）根据上述定义，“直角三角形是勾股三角形”是真命题还是假命题；
（2）已知一勾股三角形三个内角从小到大依次为x、y和z，且xy=2160，求x+y的值；
（3）如图，△ABC中，AB=，BC=2，AC=1+，求证：△ABC是勾股三角形．
【分析】（1）直接根据“勾股三角形”的定义，判断得出即可；
（2）利用已知得出等量量关系组成方程组，进而求出x+y的值；
（3）过B作BH⊥AC于H，设AH=x，利用勾股定理首先得出AH=BH=，HC=1，进而得出∠A=45°，∠C=60°，∠B=75°，即可得出结论．
【解答】（1）解：“直角三角形是勾股三角形”是假命题；理由如下：
∵对于任意的三角形，设其三个角的度数分别为x°、y°和z°，
若满足x2+y2=z2，则称这个三角形为勾股三角形，
∴无法得到，所有直角三角形是勾股三角形，故是假命题；
（2）解：由题意可得：，
解得：x+y=102；
（3）证明：过B作BH⊥AC于H，如图所示：
设AH=x
Rt△ABH中，BH=，
Rt△CBH中，（）2+（1+﹣x）2=4，
解得：x=，
∴AH=BH=，HC=1，
∴∠A=∠ABH=45°，
∴tan∠HBC===，
∴∠HBC=30°，
∴∠BCH=60°，∠B=75°，
∴452+602=752
∴△ABC是勾股三角形．
【点评】此题主要考查了新定义、多元方程组解法、勾股定理和锐角三角函数关系，利用勾股定理得出AH，HC的长是解题关键．
　
25．（2016春?临清市期中）如图：四边形ABCD中，AB=CB=，CD=，DA=1，且AB⊥CB于B．
试求：（1）∠BAD的度数；
（2）四边形ABCD的面积．
【分析】连接AC，则在直角△ABC中，已知AB，BC可以求AC，根据AC，AD，CD的长可以判定△ACD为直角三角形，
（1）根据∠BAD=∠CAD+∠BAC，可以求解；
（2）根据四边形ABCD的面积为△ABC和△ACD的面积之和可以解题．
【解答】解：（1）连接AC，
∵AB⊥CB于B，
∴∠B=90°，
在△ABC中，∵∠B=90°，
∴AB2+BC2=AC2，
又∵AB=CB=，
∴AC=2，∠BAC=∠BCA=45°，
∵CD=，DA=1，
∴CD2=5，DA2=1，AC2=4．
∴AC2+DA2=CD2，
由勾股定理的逆定理得：∠DAC=90°，
∴∠BAD=∠BAC+∠DAC=45°+90°=135°；
（2）∵∠DAC=90°，AB⊥CB于B，
∴S△ABC=，S△DAC=，
∵AB=CB=，DA=1，AC=2，
∴S△ABC=1，S△DAC=1
而S四边形ABCD=S△ABC+S△DAC，
∴S四边形ABCD=2．
【点评】本题考查了勾股定理在直角三角形中的运用，考查了根据勾股定理逆定理判定直角三角形，考查了直角三角形面积的计算，本题中求证△ACD是直角三角形是解题的关键．
　
26．（2016春?孝南区校级月考）已知，如图，在四边形ABCD中，∠ABC=90°，CD⊥AD，AD2+CD2=2AB2，求证：AB=BC．2-1-c-n-j-y
【分析】由勾股定理得出AB2+BC2=AC2，AD2+CD2=AC2，再由已知条件得出AB2+BC2=2AB2，AB2=BC2，即可得出结论．
【解答】证明：∵∠ABC=90°，
∴AB2+BC2=AC2，
∵CD⊥AD，
∴∠ADC=90°，
∴AD2+CD2=AC2，
∵AD2+CD2=2AB2，
∴AC2=2AB2，
∴AB2+BC2=2AB2，
∴AB2=BC2，
∴AB=BC．
【点评】本题考查了勾股定理、线段相等的证明方法；熟练掌握勾股定理，并能进行推理论证是解决问题的关键．
　
27．已知△ABC中，AB=AC．
（1）如图1，在△ADE中，若AD=AE，且∠DAE=∠BAC，求证：CD=BE；
（2）如图2，在△ADE中，若∠DAE=∠BAC=60°，且CD垂直平分AE，AD=3，CD=4，求BD的长；
（3）如图3，在△ADE中，当BD垂直平分AE于H，且∠BAC=2∠ADB时，试探究CD2，BD2，AH2之间的数量关系，并证明．
【分析】（1）求出∠DAC=∠BAE，再利用“边角边”证明△ACD和△ABE全等，再根据全等三角形对应边相等即可得证；
（2）连接BE，先求出△ADE是等边三角形，再根据全等三角形对应边相等可得BE=CD，全等三角形对应角相等可得∠BEA=∠CDA=30°，然后求出∠BED=90°，再利用勾股定理列式进行计算即可得解；
（3）过B作BF⊥BD，且BF=AE，连接DF，先求出四边形ABFE是平行四边形，根据平行四边形对边相等可得AB=EF，设∠AEF=x，∠AED=y，根据平行四边形的邻角互补与等腰三角形的性质求出∠CAD，从而得到∠CAD=∠FED，然后利用“边角边”证明△ACD和△EFD全等，根据全等三角形对应边相等可得CD=DF，然后利用勾股定理列式计算即可得解．
【解答】（1）如图1，证明：∵∠DAE=∠BAC，
∴∠DAE+∠CAE=∠BAC+∠CAE，
即∠DAC=∠BAE．
在△ACD与△ABE中，
，
∴△ACD≌△ABE（SAS），
∴CD=BE；
（2）连接BE，
∵AD=AE，∠DAE=60°，
∴△ADE是等边三角形，
∵CD垂直平分AE，
∴∠CDA=∠ADE=×60°=30°，
∵△ABE≌△ACD，
∴BE=CD=4，∠BEA=∠CDA=30°，
∴BE⊥DE，DE=AD=3，
∴BD=5；
（3）如图，过B作BF⊥BD，且BF=AE，连接DF，
则四边形ABFE是平行四边形，
∴AB=EF，
设∠AEF=x，∠AED=y，
则∠FED=x+y，
∠BAE=180°﹣x，∠EAD=∠AED=y，∠BAC=2∠ADB=180°﹣2y，
∠CAD=360°﹣∠BAC﹣∠BAE﹣∠EAD=360°﹣（180°﹣2y）﹣（180°﹣x）﹣y=x+y，
∴∠FED=∠CAD，
在△ACD和△EFD中，
，
∴△ACD≌△EFD（SAS），
∴CD=DF，
而BD2+BF2=DF2，
∴CD2=BD2+4AH2．
【点评】本题考查了勾股定理，全等三角形的判定与 性质，线段垂直平分线上的点到线段两端点的距离相等的性质，等边三角形的判定与性质，综合性较强，难度较大，作辅助线构造出全等三角形与直角三角形是解题的关键．www.21-cn-jy.com