相似三角形的性质及应用
图片预览

文档简介
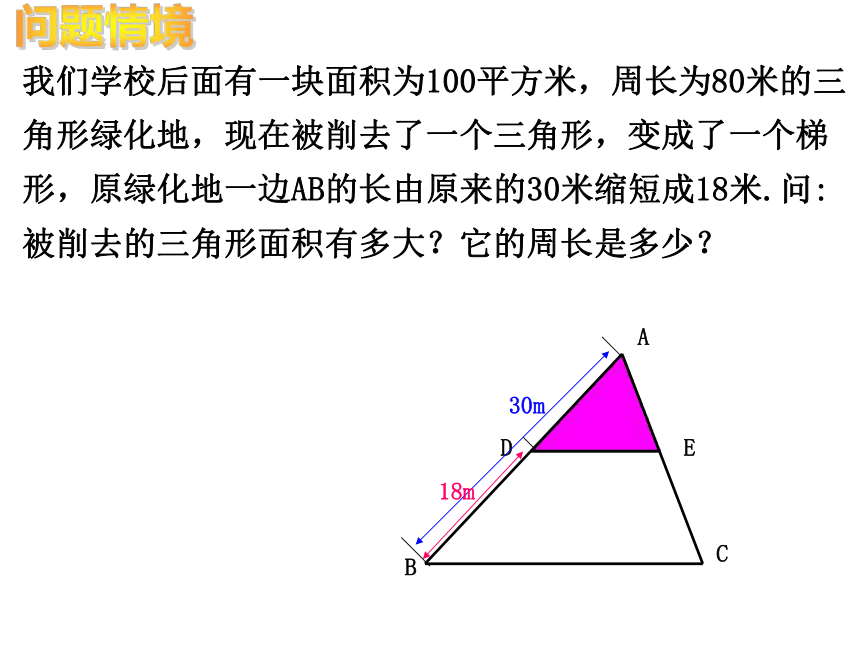
课件17张PPT。4。4相似三角形的性质及其应用(1)后洋中学 丁慧辉我们学校后面有一块面积为100平方米,周长为80米的三角形绿化地,现在被削去了一个三角形,变成了一个梯形,原绿化地一边AB的长由原来的30米缩短成18米.问:被削去的三角形面积有多大?它的周长是多少?问题情境30mΔABC与ΔA′B′C′的相似比是多少?
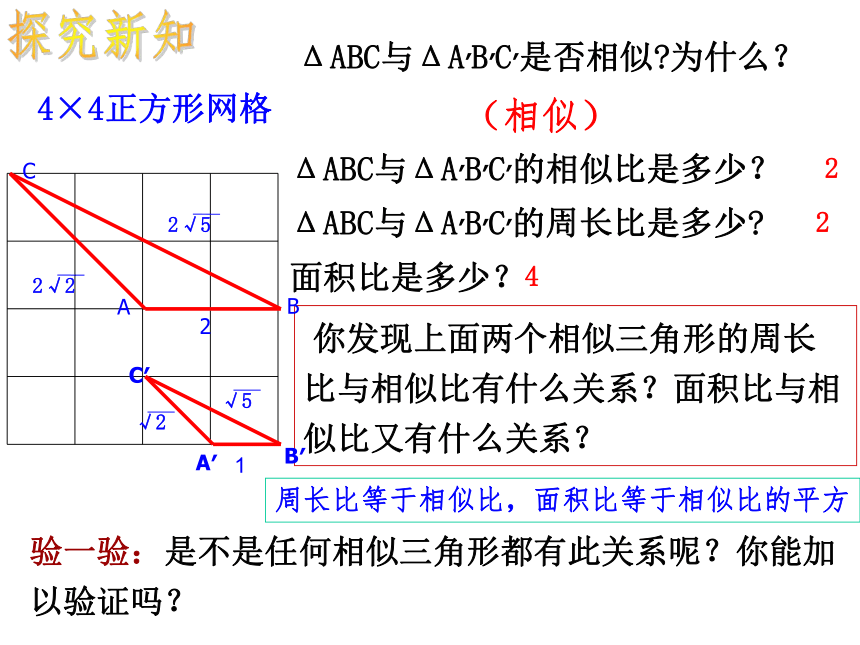
ΔABC与ΔA′B′C′的周长比是多少?
面积比是多少?4×4正方形网格ΔABC与ΔA′B′C′是否相似?为什么? 验一验:是不是任何相似三角形都有此关系呢?你能加以验证吗? 你发现上面两个相似三角形的周长比与相似比有什么关系?面积比与相似比又有什么关系?(相似)周长比等于相似比,面积比等于相似比的平方探究新知CABA′C′
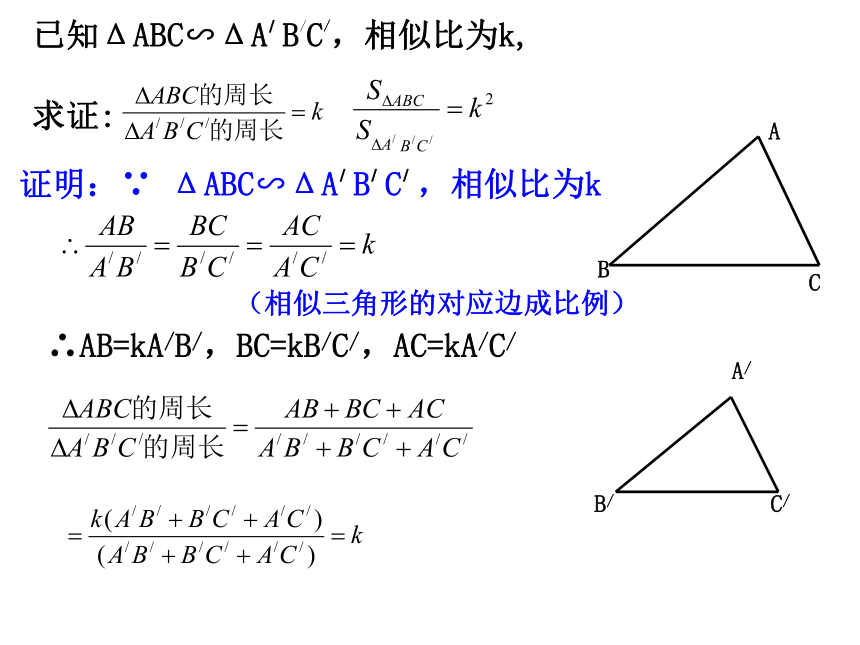
B′224A/已知ΔABC∽ΔA/ B/C/,相似比为k,
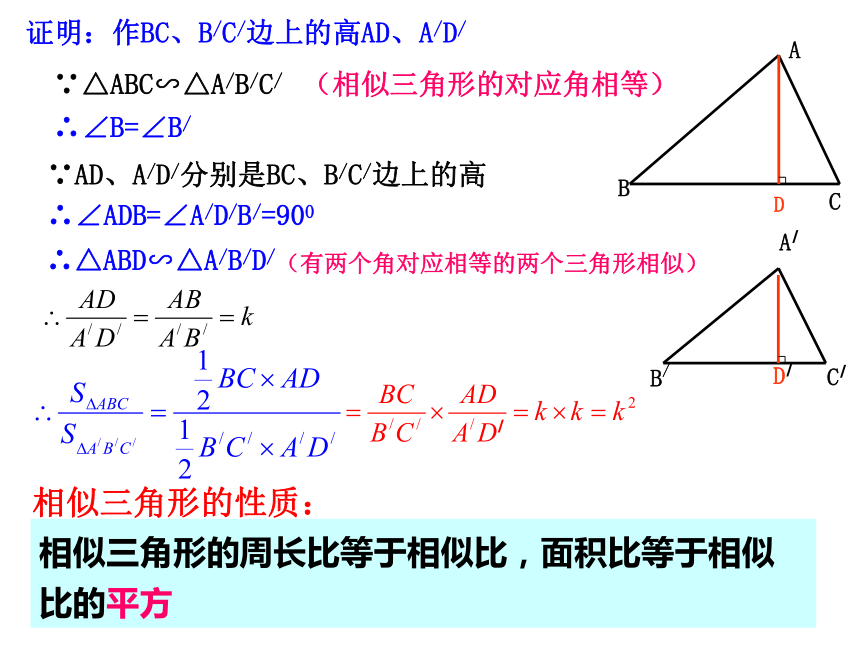
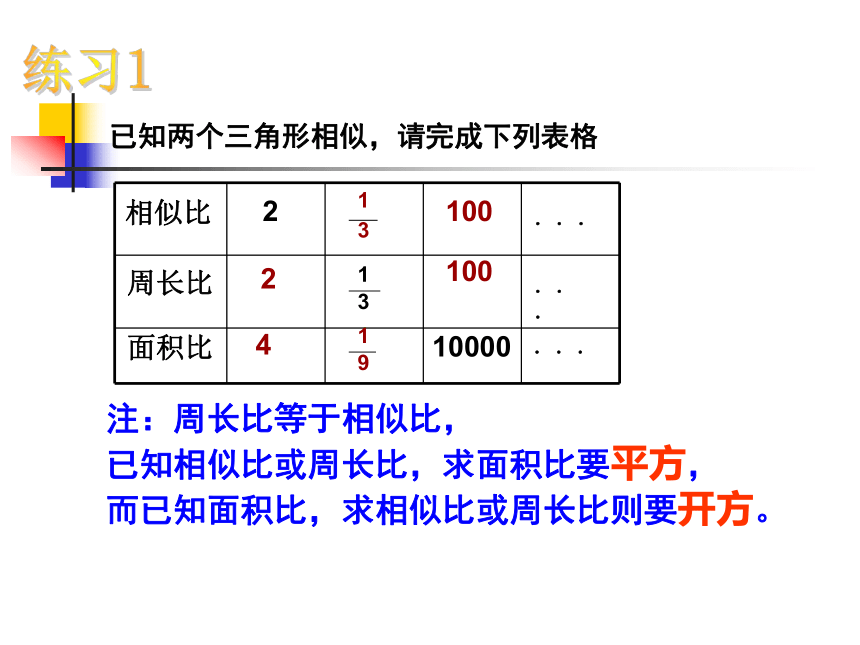
求证:证明:∵ ΔABC∽ΔA/ B/ C/ ,相似比为k∴AB=kA/B/,BC=kB/C/,AC=kA/C/(相似三角形的对应边成比例)B/C/相似三角形的周长比等于相似比,面积比等于相似比的平方证明:作BC、B/C/边上的高AD、A/D/∵△ABC∽△A/B/C/∴∠B=∠B/(相似三角形的对应角相等)∵AD、A/D/分别是BC、B/C/边上的高∴∠ADB=∠A/D/B/=900∴△ABD∽△A/B/D/相似三角形的性质:(有两个角对应相等的两个三角形相似)已知两个三角形相似,请完成下列表格相似比周长比面积比注:周长比等于相似比,
已知相似比或周长比,求面积比要平方,
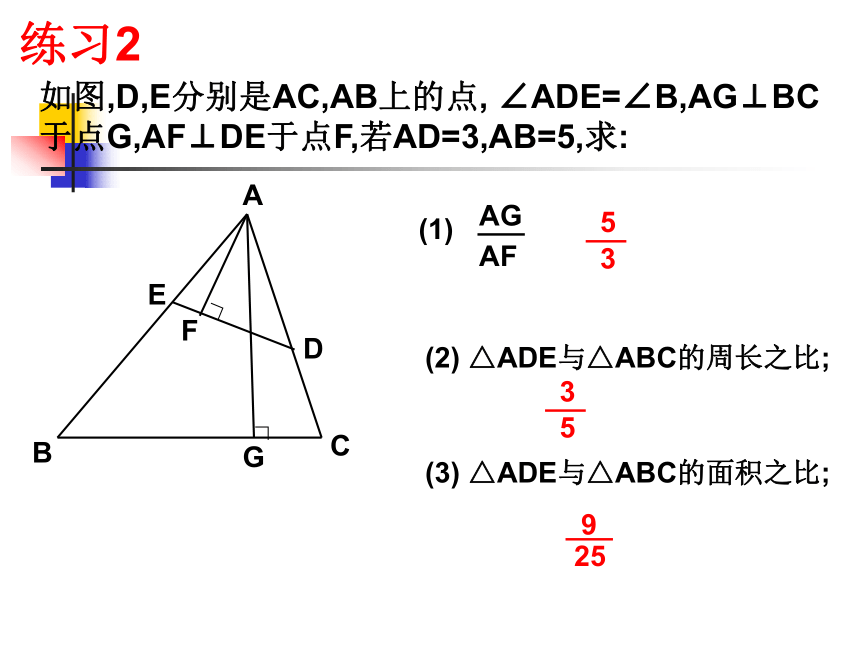
而已知面积比,求相似比或周长比则要开方。练习124100100100002.........练习2如图,D,E分别是AC,AB上的点, ∠ADE=∠B,AG⊥BC于点G,AF⊥DE于点F,若AD=3,AB=5,求:∟∟ABCGEDF(1)(2) △ADE与△ABC的周长之比;(3) △ADE与△ABC的面积之比;例1如图:是某市部分街道图,比例尺为1:10 000;请估计三条道路围成的三角形地块ABC的实际周长和面积。其中测得:AB=3.4cm, BC=3.8cm,AC=2.5cm,高AD=2.2cmCD解:△ABC的周长=3.4+3.8+2.5=9.7cm∴三角形地块的实际周长为9.7×104cm,即970m∵S△ABC=3.8×2.2÷2=4.18(cm2)∴三角形地块的实际面积为4.18×108cm2,即41800m2答:估计三角形地块的周长为970cm,实际面积为41800m2。AB探究活动 已知△ABC如图,如果要作与BC平行的直线把△ABC划分成两部分,使这两部分(三角形与四边形)的面积之比为1:1,该怎样作?如果要使划分成的两部分的面积之比为1:2呢?如果要使划分成的两部分的面积之比为1:n呢?1、在△ABC中,DE??BC,E、D分别在AC、AB上,EC=2AE,则S △ ADE:S四边形DBCE的比为______尝试运用2、如图, △ABC中,DE??FG??BC,AD=DF=FB,则S△ADE:S四边形DFGE:S四边形FBCG
= 1:3: 5如图,已知DE//BC,AB=30m,BD=18m,ΔABC的周长为80m,面积为100m2,求ΔADE的周长和面积问题解决30m答: ΔADE的周长是32m,面积为16m2小结本节课你有哪些收获? 作业当天作业: 课堂作业本
回家作业: 同步练习
挑战作业:
求证:相似三角形的对应高的比,
对应中线的比与对应角平分线的比
都等于相似比。
笛卡尔说过:我所解决的每一个问题都将成为一个范例,以用于解决其他问题,这便是学习数学的真谛!请用心体会下面这句话谢谢,再见!ADE1.过E作EF//AB交BC于F,其他条件不变,则ΔEFC的面积等于多少? 2.若设sΔABC=S, SΔADE=S1, SΔEFC=S2.请猜想:S与S1、S2之间存在怎样的关系?你能加以验证吗?BC拓展延伸36m2证明:DE//BCEF//AB1636类比猜想
ΔABC与ΔA′B′C′的周长比是多少?
面积比是多少?4×4正方形网格ΔABC与ΔA′B′C′是否相似?为什么? 验一验:是不是任何相似三角形都有此关系呢?你能加以验证吗? 你发现上面两个相似三角形的周长比与相似比有什么关系?面积比与相似比又有什么关系?(相似)周长比等于相似比,面积比等于相似比的平方探究新知CABA′C′
B′224A/已知ΔABC∽ΔA/ B/C/,相似比为k,
求证:证明:∵ ΔABC∽ΔA/ B/ C/ ,相似比为k∴AB=kA/B/,BC=kB/C/,AC=kA/C/(相似三角形的对应边成比例)B/C/相似三角形的周长比等于相似比,面积比等于相似比的平方证明:作BC、B/C/边上的高AD、A/D/∵△ABC∽△A/B/C/∴∠B=∠B/(相似三角形的对应角相等)∵AD、A/D/分别是BC、B/C/边上的高∴∠ADB=∠A/D/B/=900∴△ABD∽△A/B/D/相似三角形的性质:(有两个角对应相等的两个三角形相似)已知两个三角形相似,请完成下列表格相似比周长比面积比注:周长比等于相似比,
已知相似比或周长比,求面积比要平方,
而已知面积比,求相似比或周长比则要开方。练习124100100100002.........练习2如图,D,E分别是AC,AB上的点, ∠ADE=∠B,AG⊥BC于点G,AF⊥DE于点F,若AD=3,AB=5,求:∟∟ABCGEDF(1)(2) △ADE与△ABC的周长之比;(3) △ADE与△ABC的面积之比;例1如图:是某市部分街道图,比例尺为1:10 000;请估计三条道路围成的三角形地块ABC的实际周长和面积。其中测得:AB=3.4cm, BC=3.8cm,AC=2.5cm,高AD=2.2cmCD解:△ABC的周长=3.4+3.8+2.5=9.7cm∴三角形地块的实际周长为9.7×104cm,即970m∵S△ABC=3.8×2.2÷2=4.18(cm2)∴三角形地块的实际面积为4.18×108cm2,即41800m2答:估计三角形地块的周长为970cm,实际面积为41800m2。AB探究活动 已知△ABC如图,如果要作与BC平行的直线把△ABC划分成两部分,使这两部分(三角形与四边形)的面积之比为1:1,该怎样作?如果要使划分成的两部分的面积之比为1:2呢?如果要使划分成的两部分的面积之比为1:n呢?1、在△ABC中,DE??BC,E、D分别在AC、AB上,EC=2AE,则S △ ADE:S四边形DBCE的比为______尝试运用2、如图, △ABC中,DE??FG??BC,AD=DF=FB,则S△ADE:S四边形DFGE:S四边形FBCG
= 1:3: 5如图,已知DE//BC,AB=30m,BD=18m,ΔABC的周长为80m,面积为100m2,求ΔADE的周长和面积问题解决30m答: ΔADE的周长是32m,面积为16m2小结本节课你有哪些收获? 作业当天作业: 课堂作业本
回家作业: 同步练习
挑战作业:
求证:相似三角形的对应高的比,
对应中线的比与对应角平分线的比
都等于相似比。
笛卡尔说过:我所解决的每一个问题都将成为一个范例,以用于解决其他问题,这便是学习数学的真谛!请用心体会下面这句话谢谢,再见!ADE1.过E作EF//AB交BC于F,其他条件不变,则ΔEFC的面积等于多少? 2.若设sΔABC=S, SΔADE=S1, SΔEFC=S2.请猜想:S与S1、S2之间存在怎样的关系?你能加以验证吗?BC拓展延伸36m2证明:DE//BCEF//AB1636类比猜想
同课章节目录
