2.2 切线长定理学案1(无答案)
图片预览

文档简介
2.2切线长定理
学案
学习目标:
1..通过操作经历切线长定理的探索过程。
2.会用切线长定理进行简单
的推理论证和
有关计算。即看见从圆外一点引了圆的两条切线能得到有关
的直接结论与间接结论。
3.能
掌握本节课的常见重点图形。
4.通过完成自主探究的5明白探索结论型的题目的思路是观察,猜想,证明。
5.通过完成自主探究的6明白几何题目可以用代数法(方程思想)解决。
学习过程:
一
自主探究,明确疑难。
1,操作。
在一张纸上画一个⊙O,在⊙O上任取一点A,过点A作⊙O的切线PA,再沿直线PO将⊙O对折,设⊙O上与点A重合的点为
B,然后将纸展开铺平,连接PB,OA,OB。
2提出问题。由1可知道
OB是⊙O的一条半径
吗?
PB是⊙O的一条切线吗?
经过点P的切线有几条?那么
是不是过圆外一点可以引圆的两条切线?
你发现PA,PB的长有什么关系?
∠APO与∠BPO相等吗?
上述结论的理由是什么?
掌握概念:点到圆的切线长。
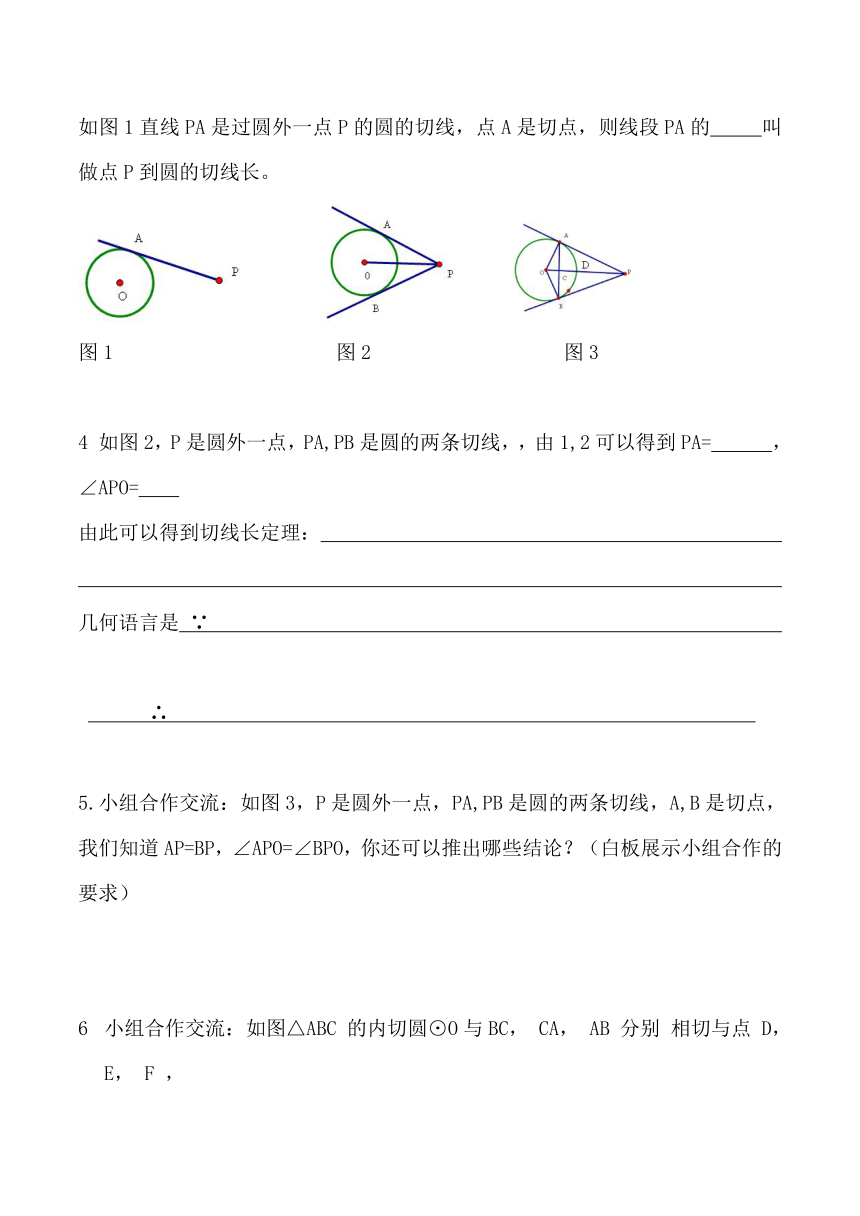
如图1直线PA是过圆外一点P的圆的切线,点A是切点,则线段PA的
叫做点P到圆的切线长。
图1
图2
图3
4
如图2,P是圆外一点,PA,PB是圆的两条切线,,由1,2可以得到PA=
,∠APO=
由此可以得到切线长定理:
几何语言是
∵
∴
小组合作交流:如图3,P是圆外一点,PA,PB是圆的两条切线,A,B是切点,我们知道AP=BP,∠APO=∠BPO,你还可以推出哪些结论?(白板展示小组合作的要求)
小组合作交流:如图△ABC
的内切圆⊙O与BC,
CA,
AB
分别
相切与点
D,
E,
F
,
且BC=a
AC=b
AB=c
则BD=
图4
二
交流展示,形成规律。
交流学习成果
小组展示(语言及掌声鼓励与小组分数奖励)
2.补充完善,揭示规律。
教师点拨(重点强调应用)
1.切线长定理(直接结论2个与多个间接结论,有关
的辅助线3条)
2.自主探究的5明白探索结论型的题目的思路是观察,猜想,证明
3.自主探究的6明白几何题目可以用代数法(方程思想)解决
三
运用规律
巩固新知
初步应用
如图5,P是圆外一点,PA,PB是圆的两条切线,A,B是切点,∠APO=350,,则∠APB=
PA=10
则PB=
。
图5
图6
已知⊙O的半径为3,点P和圆心O
的距离为6,过P点引⊙O的一条切线,则这条切线的长为
如图6
,P是圆外一点,PA,PB是圆的两条切线,,OP交⊙O于
点C,写出5
个正确
的结论(不再
添加字母)
2
练习拓展
课本课内练习1,2.
课本作业题1,2.
3.课本习题3.及试一试
四
自我评价
检测反馈
学习体会
本
节
课有什么收获?有什么困惑?
当堂检测
如图7
,P是圆外一点,PA,PB是圆的两条切线,OP交AB于
点C,则图中相等的线段有(
)对。
(A
)1
(
B
)
2
(
C
)
3
(
D
)
4
图7
图8
2.如图7,P是圆外一点,PA,PB是圆的两条切线,A,B是切点,∠APB=600
⊙O的半径是3,则PA
的长
为
3如图8,P是圆外一点,PA,PB是圆的两条切线,A,B是切点,CD切⊙O于
E
,∠APB=500
则∠COD的度数
是
。如果AP=8,则△PCE的周长等于
.
4
如图9,△ABC
的内切圆⊙O与BC,
CA,
AB
分别
相切与点
D,
E,
F
,且AB
=9
BC=14
CA=13
,求AF
,
BD
,CE
的长?
图9
学案
学习目标:
1..通过操作经历切线长定理的探索过程。
2.会用切线长定理进行简单
的推理论证和
有关计算。即看见从圆外一点引了圆的两条切线能得到有关
的直接结论与间接结论。
3.能
掌握本节课的常见重点图形。
4.通过完成自主探究的5明白探索结论型的题目的思路是观察,猜想,证明。
5.通过完成自主探究的6明白几何题目可以用代数法(方程思想)解决。
学习过程:
一
自主探究,明确疑难。
1,操作。
在一张纸上画一个⊙O,在⊙O上任取一点A,过点A作⊙O的切线PA,再沿直线PO将⊙O对折,设⊙O上与点A重合的点为
B,然后将纸展开铺平,连接PB,OA,OB。
2提出问题。由1可知道
OB是⊙O的一条半径
吗?
PB是⊙O的一条切线吗?
经过点P的切线有几条?那么
是不是过圆外一点可以引圆的两条切线?
你发现PA,PB的长有什么关系?
∠APO与∠BPO相等吗?
上述结论的理由是什么?
掌握概念:点到圆的切线长。
如图1直线PA是过圆外一点P的圆的切线,点A是切点,则线段PA的
叫做点P到圆的切线长。
图1
图2
图3
4
如图2,P是圆外一点,PA,PB是圆的两条切线,,由1,2可以得到PA=
,∠APO=
由此可以得到切线长定理:
几何语言是
∵
∴
小组合作交流:如图3,P是圆外一点,PA,PB是圆的两条切线,A,B是切点,我们知道AP=BP,∠APO=∠BPO,你还可以推出哪些结论?(白板展示小组合作的要求)
小组合作交流:如图△ABC
的内切圆⊙O与BC,
CA,
AB
分别
相切与点
D,
E,
F
,
且BC=a
AC=b
AB=c
则BD=
图4
二
交流展示,形成规律。
交流学习成果
小组展示(语言及掌声鼓励与小组分数奖励)
2.补充完善,揭示规律。
教师点拨(重点强调应用)
1.切线长定理(直接结论2个与多个间接结论,有关
的辅助线3条)
2.自主探究的5明白探索结论型的题目的思路是观察,猜想,证明
3.自主探究的6明白几何题目可以用代数法(方程思想)解决
三
运用规律
巩固新知
初步应用
如图5,P是圆外一点,PA,PB是圆的两条切线,A,B是切点,∠APO=350,,则∠APB=
PA=10
则PB=
。
图5
图6
已知⊙O的半径为3,点P和圆心O
的距离为6,过P点引⊙O的一条切线,则这条切线的长为
如图6
,P是圆外一点,PA,PB是圆的两条切线,,OP交⊙O于
点C,写出5
个正确
的结论(不再
添加字母)
2
练习拓展
课本课内练习1,2.
课本作业题1,2.
3.课本习题3.及试一试
四
自我评价
检测反馈
学习体会
本
节
课有什么收获?有什么困惑?
当堂检测
如图7
,P是圆外一点,PA,PB是圆的两条切线,OP交AB于
点C,则图中相等的线段有(
)对。
(A
)1
(
B
)
2
(
C
)
3
(
D
)
4
图7
图8
2.如图7,P是圆外一点,PA,PB是圆的两条切线,A,B是切点,∠APB=600
⊙O的半径是3,则PA
的长
为
3如图8,P是圆外一点,PA,PB是圆的两条切线,A,B是切点,CD切⊙O于
E
,∠APB=500
则∠COD的度数
是
。如果AP=8,则△PCE的周长等于
.
4
如图9,△ABC
的内切圆⊙O与BC,
CA,
AB
分别
相切与点
D,
E,
F
,且AB
=9
BC=14
CA=13
,求AF
,
BD
,CE
的长?
图9
