3.2 实数课件（共22张PPT）

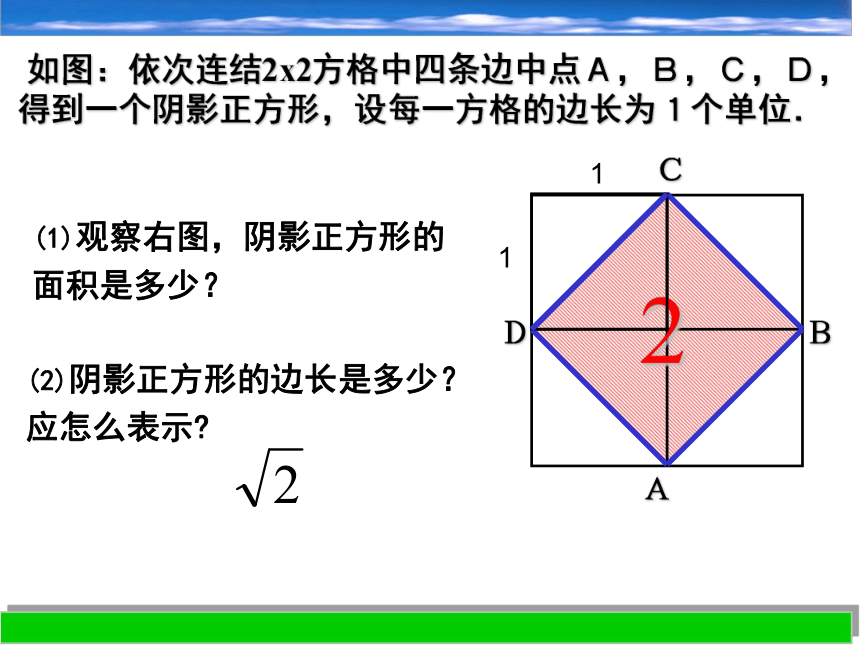
课件22张PPT。3.2 实数(1)观察右图，阴影正方形的面积是多少？(2)阴影正方形的边长是多少？应怎么表示?　如图：依次连结2x2方格中四条边中点Ａ，Ｂ，Ｃ，Ｄ，得到一个阴影正方形，设每一方格的边长为１个单位．ＡＢＣＤ2S1=S2=S3= 1 2124即 介于1和2之间探究 介于哪两个整数之间？探究 到底是一个什么样的数？12=1, ( )2=2, 22=41.412=1.9881, ( )2=2, 1.422=2.01641.41< <1.42 1.42=1.96 ( )2=2, 1.52=2.251.4< <1.51< < 2=1. =1.4=1.41
1.414 213 562 373 095 048 801 688 724 209 6……我们把这种无限不循环小数叫做无理数。=它既不是有限小数,也不是无限循环小数　也就是说 不是有理数
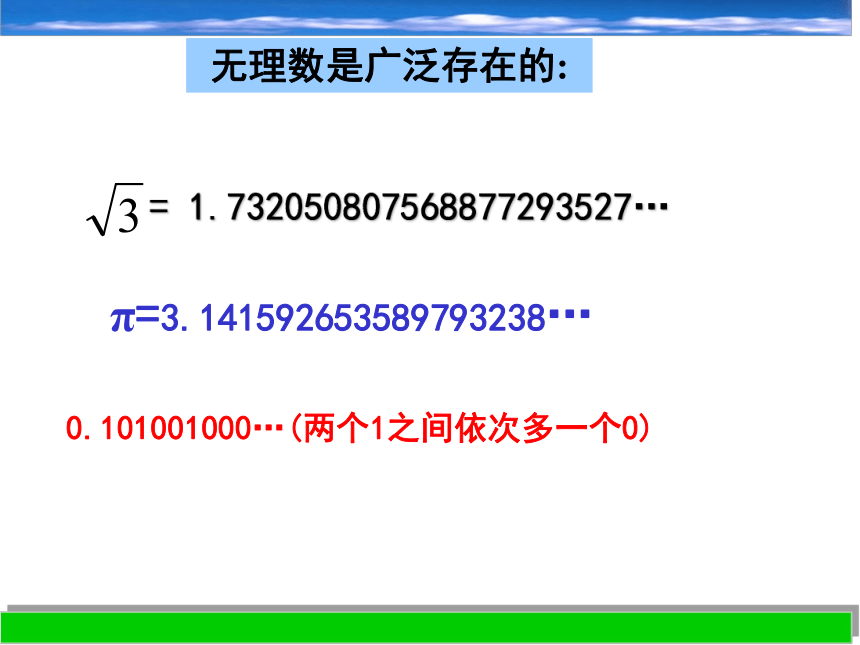
0.101001000…(两个1之间依次多一个0)π=3.141592653589793238…= 1.732050807568877293527…无理数是广泛存在的:无理数可分为正无理数和负无理数有理数和无理数统称为实数 数的扩充如: , ,π是正无理数. -π,- ,- 是负无理数 .
, -8，5， , -3.61， ,
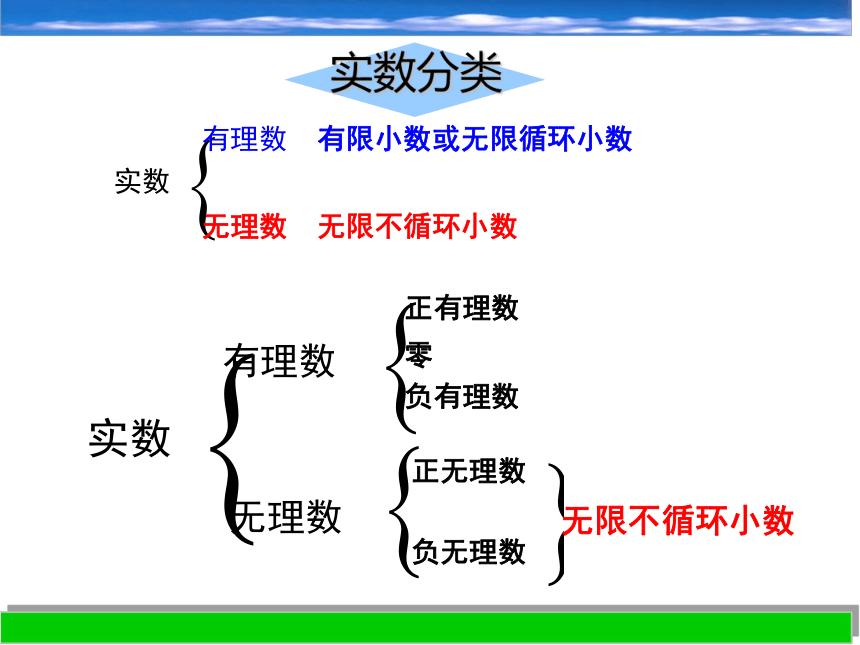
０，29 ,　 实数有理数无理数,-8，5， ,０，29 , -3.61,有限小数或无限循环小数无限不循环小数将下列各实数按一定角度分类,1.313113…（两个3之间依次多一个1）..实数有理数无理数有限小数或无限循环小数无限不循环小数实数有理数无理数正有理数负有理数零正无理数负无理数无限不循环小数实数分类 把数从有理数扩充到实数以后,有理数中的相反数和绝对值在实数中具有相同的意义.如 : 和 是互为相反数 . ==填空：
（1） 的相反数是_____
（2） 的相反数是_____
（3） ______
（4）绝对值等于 的数是_________速度大比拼无理数是否也可以用数轴上的点表示出来呢?
能否把 ,π表示在数轴上呢?　ＡＢＣＤ2边长为1个单位小正方形的对角线= -2 -1 0 1 2 3 4 5··实数 数轴上的点一一对应数轴上的每一个点都表示一个实数。每一个实数都可以用数轴上的一个点来表示。 把下列实数表示在数轴上,并比较它们　 的大小(用“＜”连接)
1.4 , , 3.3 , - , 1.5 ,在数轴上表示的两个实数，右边的数总比左边的数大。例两个无理数的和一定是无理数。（ ）两个无理数的积一定是无理数。（ ）××判断下面的说法是否正确,并举例说明理由.这节课我们都学了
哪些知识？我们来谈谈1.作业本
2.书本课后题布置作业:祖冲之
(南北朝) 刘徽
（魏晋时期） 阿基米德
（古希腊） ??刘徽（约公元3世纪）首创了一种割圆术的数学方法，算出π的近似值为3.1416，计算圆周率精确到了小数点后第3位（后人称之为徽率）。割圆术的数学思想，用刘徽的原话讲就是：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”实际上，割圆术已孕育了微积分的思想。
祖冲之（公元429—500年）是继刘徽之后的一位杰出的数学家，他把刘徽创造的割圆术成果又向前推进了一步，计算圆周率精确到小数点后第七位，即3.1415926<π <3.1415927 还得到π的两个近似值：约率22/7 和密率355/113 。密率是一个很好的近似分数值，它是分子分母在1000以内最接近π值的分数． 1593年，也就是1000多年后，才被德国数学家鄂图（otto）重新得到。无理数是否也可以用数轴上的点表示出来呢?大的正方形边长=小正方形的对角线=边长为１个单位长度