增长率问题和四边形中的动点问题(解析版)
文档属性
| 名称 | 增长率问题和四边形中的动点问题(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 224.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-01 08:55:02 | ||
图片预览


文档简介
增长率问题和四边形中的动点问题20160610
一.解答题(共19小题)
1.(2016 宝应县一模)某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.6万元,设可变成本平均每年增长的百分率为x.
(1)用含x的代数式表示第3年的可变成本为 万元;
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年增长的百分率x.
2.(2016 临沭县校级一模)某企业2010年盈利1500万元,2012年克服全球金融危机的不利影响,仍实现盈利2160万元.从2010年到2012年,如果该企业每年盈利的年增长率相同,求:
(1)该企业2011年盈利多少万元?
(2)若该企业盈利的年增长率继续保持不变,预计2013年盈利多少万元?
3.(2016 安徽四模)随着市民环保意识的增强,烟花爆竹销售量逐年下降.常德市2012年销售烟花爆竹20万箱,到2014年烟花爆竹销售量为9.8万箱.求常德市2012年到2014年烟花爆竹年销售量的平均下降率.
4.(2016 景德镇校级二模)某地区2014年投入教育经费1000万元,至2016年三年总计投入教育经费3640万元,假设2014年至2016年该地区投入教育经费的平均增长率相同,根据这个年平均增长率,预计2017年该地区将投入教育经费多少万元?
5.(2015 柳州)如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=12cm,BC=18cm,点P从点A出发以2cm/s的速度沿A→D→C运动,点P从点A出发的同时点Q从点C出发,以1cm/s的速度向点B运动,当点P到达点C时,点Q也停止运动.设点P,Q运动的时间为t秒.
(1)从运动开始,当t取何值时,PQ∥CD?
(2)从运动开始,当t取何值时,△PQC为直角三角形?
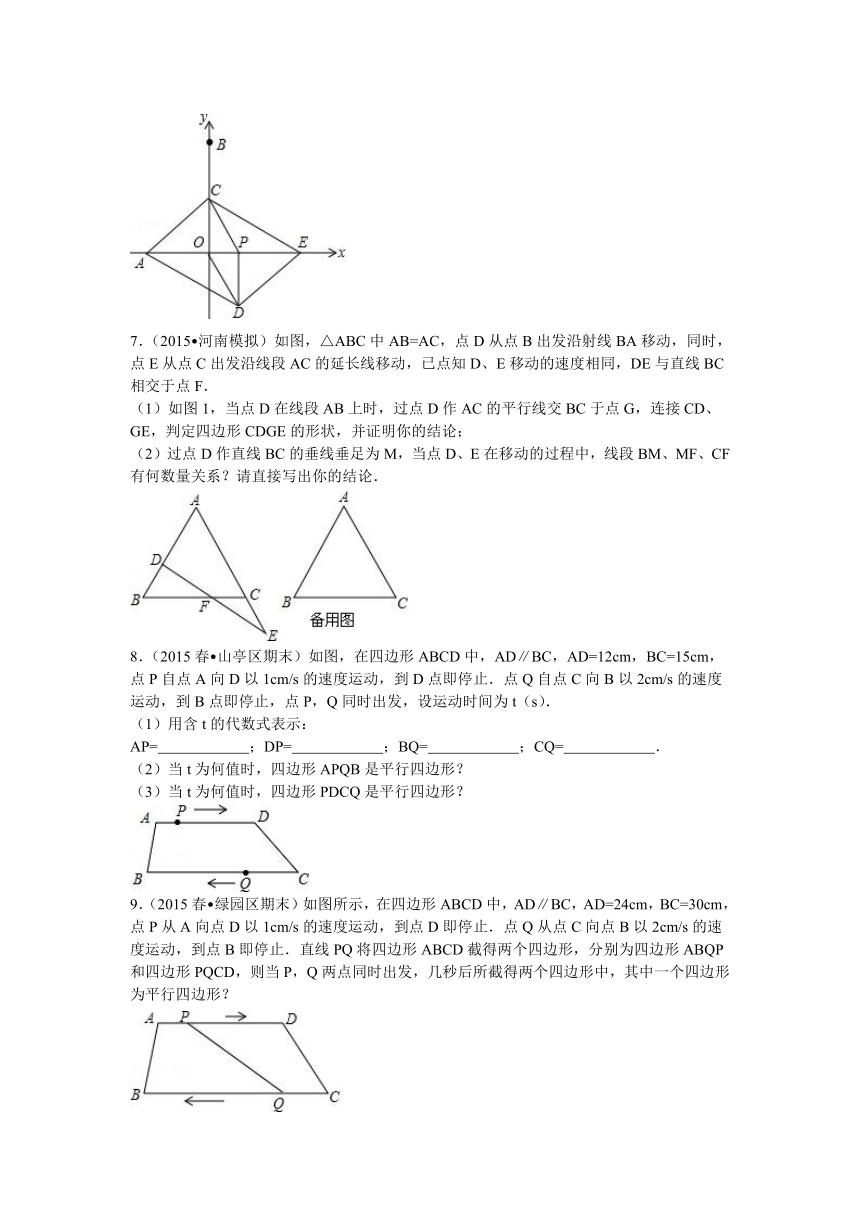
6.(2015 昌邑市校级模拟)如图,在平面直角坐标系中,点A,B的坐标分别是(﹣3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造□PCOD.在线段OP延长线上一动点E,且满足PE=AO.
(1)当点C在线段OB上运动时,求证:四边形ADEC为平行四边形;
(2)当点P运动的时间为秒时,求此时四边形ADEC的周长是多少?
7.(2015 河南模拟)如图,△ABC中AB=AC,点D从点B出发沿射线BA移动,同时,点E从点C出发沿线段AC的延长线移动,已点知D、E移动的速度相同,DE与直线BC相交于点F.
(1)如图1,当点D在线段AB上时,过点D作AC的平行线交BC于点G,连接CD、GE,判定四边形CDGE的形状,并证明你的结论;
(2)过点D作直线BC的垂线垂足为M,当点D、E在移动的过程中,线段BM、MF、CF有何数量关系?请直接写出你的结论.
8.(2015春 山亭区期末)如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP= ;DP= ;BQ= ;CQ= .
(2)当t为何值时,四边形APQB是平行四边形?
(3)当t为何值时,四边形PDCQ是平行四边形?
9.(2015春 绿园区期末)如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从A向点D以1cm/s的速度运动,到点D即停止.点Q从点C向点B以2cm/s的速度运动,到点B即停止.直线PQ将四边形ABCD截得两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形?
10.(2015 杭州模拟)如图,平行四边形ABCD中,AC=6,BD=8,点P从点A出发以每秒1cm的速度沿射线AC移动,点Q从点C出发以每秒1cm的速度沿射线CA移动.
(1)经过几秒,以P,Q,B,D为顶点的四边形为矩形?
(2)若BC⊥AC垂足为C,求(1)中矩形边BQ的长.
11.(2015春 长清区期末)如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1cm/s的速度运动,点Q从C点开始沿CB边向B以2cm/s的速度运动,如果P、Q分别从A、C同时出发,设运动时间为t秒.
求:(1)当t为何值时,四边形ABQP为矩形?
(2)当t为何值时,四边形PQCD为平行四边形?
12.(2016 开江县二模)如图,在△ABD中,AB=AD,AO平分∠BAD,过点D作AB的平行线交AO的延长线于点C,连接BC.
(1)求证:四边形ABCD是菱形;
(2)如果OA,OB(OA>OB)的长(单位:米)是一元二次方程x2﹣7x+12=0的两根,求AB的长以及菱形ABCD的面积;
(3)若动点M从A出发,沿AC以2m/S的速度匀速直线运动到点C,动点N从B出发,沿BD以1m/S的速度匀速直线运动到点D,当M运动到C点时运动停止.若M、N同时出发,问出发几秒钟后,△MON的面积为?
13.(2016春 丹阳市校级月考)如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点B出发,沿BA方向以每秒cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设Q点运动的时间t秒,若四边形QPBP′为菱形,求t的值多少秒?并说明理由.
14.(2016春 江阴市校级月考)如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=16cm,BC=22cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒.
(1)当t为多少时,四边形ABQP成为矩形?
(2)四边形PBQD是否能成为菱形?若能,求出t的值;若不能,请说明理由,并探究如何改变Q点的速度(匀速运动),使四边形PBQD在某一时刻为菱形,求点Q的速度.
15.(2015 元阳县校级一模)如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,点P从点A出发,以1cm/s的速度向点D运动(不与D重合).设点P运动的时间为t秒,请用t表示PD的长;
(3)当t为何值时,四边形PBQD是菱形?
16.(2015 郑州校级三模)如图,在△ABC中,AB=AC=10cm,BC=12cm,E是BA延长线的一点.
(1)利用尺规∠EAC的平分线AD(保留作图痕迹,不写作法);
(2)若点P在射线AD上从点A开始运动,点Q在线段CB上从点C向点点B运动,运动的速度均为1cm/s,运动时间为t,若P、Q同时运动.
①连接PQ交AC于点O.求证:AO=CO;
②填空:当t= 秒时四边形APCQ一定是矩形;
③填空:当t= 秒时四边形APCQ一定是菱形.
17.(2015春 江西期末)如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以lcm/s的速度运动,同时点F从点B出发沿线射BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)当t为多少时,四边形ACFE是菱形.
18.(2015春 日照期末)如图,矩形ABCD中,对角线AC、BD相交于点O,点P是线段AD上一动点(不与与点D重合),PO的延长线交BC于Q点.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=6cm,AD=8cm,P从点A出发.以1cm/秒的速度向点D匀速运动.设点P运动时间为t秒,问四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
19.(2014春 兴业县期末)如图,已知△ABC和△DEF是两个边长为10cm的等边三角形,且B、D、C、E都在同一直线上.连接AD、CF.
(1)求证:四边形ADFC是平行四边形;
(2)若BD=4cm,△ABC沿着BE的方向以每秒2cm的速度运动,设△ABC运动时间为t秒,当t为何值时, ADFC是菱形?请说明你的理由.
增长率问题和四边形中的动点问题20160610
参考答案与试题解析
一.解答题(共19小题)
1.(2016 宝应县一模)某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.6万元,设可变成本平均每年增长的百分率为x.
(1)用含x的代数式表示第3年的可变成本为 2.6(1+x)2 万元;
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年增长的百分率x.
【分析】(1)根据增长率问题由第1年的可变成本为2.6万元就可以表示出第二年的可变成本为2.6(1+x),则第三年的可变成本为2.6(1+x)2,故得出答案;
(2)根据养殖成本=固定成本+可变成本建立方程求出其解即可
【解答】解:(1)由题意,得
第3年的可变成本为:2.6(1+x)2,
故答案为:2.6(1+x)2;
(2)由题意,得
4+2.6(1+x)2=7.146,
解得:x1=0.1,x2=﹣2.1(不合题意,舍去).
答:可变成本平均每年增长的百分率为10%.
2.(2016 临沭县校级一模)某企业2010年盈利1500万元,2012年克服全球金融危机的不利影响,仍实现盈利2160万元.从2010年到2012年,如果该企业每年盈利的年增长率相同,求:
(1)该企业2011年盈利多少万元?
(2)若该企业盈利的年增长率继续保持不变,预计2013年盈利多少万元?
【分析】(1)设每年盈利的年增长率为x,就可以表示出2012年的盈利,根据2012年的盈利为2160万元建立方程求出x的值就可以求出2011年的盈利;
(2)根据(1)求出的年增长率就可以求出结论.
【解答】(1)设每年盈利的年增长率为x,根据意,得
1500(1+x)2=2160
解得:x1=0.2,x2=﹣2.2(不合题意,舍去)
∴该企业2011年盈利为:1500(1+0.2)=1800万元.
答:2011年该企业盈利1800万元;
(2)由题意,得
2160(1+0.2)=2592万元
答:预计2013年该企业盈利2592万元.
3.(2016 安徽四模)随着市民环保意识的增强,烟花爆竹销售量逐年下降.常德市2012年销售烟花爆竹20万箱,到2014年烟花爆竹销售量为9.8万箱.求常德市2012年到2014年烟花爆竹年销售量的平均下降率.
【分析】先设常德市2012年到2014年烟花爆竹年销售量的平均下降率是x,那么把2012年的烟花爆竹销售量看做单位1,在此基础上可求2013年的年销售量,以此类推可求2014年的年销售量,而2014年烟花爆竹销售量为9.8万箱,据此可列方程,解即可.
【解答】解:设常德市2012年到2014年烟花爆竹年销售量的平均下降率是x,依题意得
20(1﹣x)2=9.8,
解这个方程,得x1=0.3,x2=1.7,
由于x2=1.7不符合题意,即x=0.3=30%.
答:常德市2012年到2014年烟花爆竹年销售量的平均下降率为30%.
4.(2016 景德镇校级二模)某地区2014年投入教育经费1000万元,至2016年三年总计投入教育经费3640万元,假设2014年至2016年该地区投入教育经费的平均增长率相同,根据这个年平均增长率,预计2017年该地区将投入教育经费多少万元?
【分析】一般用增长后的量=增长前的量×(1+增长率),2015年要投入教育经费是1000(1+x)万元,在2016年的基础上再增长x,就是2016年的教育经费数额,即可列出方程求解.利用求得的增长率来求2017年该地区将投入教育经费.
【解答】解:设增长率为x,根据题意可得:1000+1000(1+x)+1000(1+x)2=3640,
化简得:25x2+75x﹣16=0,
解得:(舍去),
所以2016年该地区投入教育经费为,
根据所得的年平均增长率,预计2017年该地区将投入教育经费为1440×1.2=1728万元.
答:2017年该地区将投入教育经费1728万元.
5.(2015 柳州)如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=12cm,BC=18cm,点P从点A出发以2cm/s的速度沿A→D→C运动,点P从点A出发的同时点Q从点C出发,以1cm/s的速度向点B运动,当点P到达点C时,点Q也停止运动.设点P,Q运动的时间为t秒.
(1)从运动开始,当t取何值时,PQ∥CD?
(2)从运动开始,当t取何值时,△PQC为直角三角形?
【分析】(1)已知AD∥BC,添加PD=CQ即可判断以PQDC为顶点的四边形是平行四边形.
(2)点P处可能为直角,点Q处也可能是直角,而后求解即可.
【解答】解:(1)当PQ∥CD时,四边形PDCB是平行四边形,
此时PD=QC,
∴12﹣2t=t,
∴t=4.
∴当t=4时,四边形PQDC是平行四边形.
(2)过D点,DF⊥BC于F,
∴DF=AB=8.
FC=BC﹣AD=18﹣12=6,CD=10,
①当PQ⊥BC,
则BQ+CQ=18.即:2t+t=18,
∴t=6;
②当QP⊥PC,此时P一定在DC上,
CP1=10+12﹣2t=22﹣2t,CQ2=t,
易知,△CDF∽△CQ2P1,
∴,
解得:t=,
③情形:当PC⊥BC时,因∠DCB<90°,此种情形不存在.
∴当t=6或时,△PQC是直角三角形.
6.(2015 昌邑市校级模拟)如图,在平面直角坐标系中,点A,B的坐标分别是(﹣3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造□PCOD.在线段OP延长线上一动点E,且满足PE=AO.
(1)当点C在线段OB上运动时,求证:四边形ADEC为平行四边形;
(2)当点P运动的时间为秒时,求此时四边形ADEC的周长是多少?
【分析】(1)连接CD交AE于F,根据平行四边形的性质得到CF=DP,OF=PF,根据题意得到AF=EF,又CF=DP,根据平行四边形的判定定理证明即可;
(2)根据题意计算出OC、OP的长,根据勾股定理求出AC、CE,根据平行四边形的周长公式计算即可.
【解答】(1)证明:连接CD交AE于F,
∵四边形PCOD是平行四边形,
∴CF=DF,OF=PF,
∵PE=AO,
∴AF=EF,又CF=DP,
∴四边形ADEC为平行四边形;
(2)解:当点P运动的时间为秒时,OP=,OC=3,
则OE=,
由勾股定理得,AC==3,
CE==,
∵四边形ADEC为平行四边形,
∴周长为(3+)×2=6+.
7.(2015 河南模拟)如图,△ABC中AB=AC,点D从点B出发沿射线BA移动,同时,点E从点C出发沿线段AC的延长线移动,已点知D、E移动的速度相同,DE与直线BC相交于点F.
(1)如图1,当点D在线段AB上时,过点D作AC的平行线交BC于点G,连接CD、GE,判定四边形CDGE的形状,并证明你的结论;
(2)过点D作直线BC的垂线垂足为M,当点D、E在移动的过程中,线段BM、MF、CF有何数量关系?请直接写出你的结论.
【分析】(1)由题意得出BD=CE,由平行线的性质得出∠DGB=∠ACB,由等腰三角形的性质得出∠B=∠ACB,得出∠B=∠DGB,证出BD=GD=CE,即可得出结论;
(2)由(1)得:BD=GD=CE,由等腰三角形的三线合一性质得出BM=GM,由平行线得出GF=CF,即可得出结论.
【解答】解:(1)四边形CDGE是平行四边.理由如下:如图1所示:
∵D、E移动的速度相同,
∴BD=CE,
∵DG∥AE,
∴∠DGB=∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠DGB,
∴BD=GD=CE,
又∵DG∥CE,
∴四边形CDGE是平行四边形;
(2)BM+CF=MF;理由如下:如图2所示:
由(1)得:BD=GD=CE,
∵DM⊥BC,
∴BM=GM,
∵DG∥AE,
∴GF=CF,
∴BM+CF=GM+GF=MF.
8.(2015春 山亭区期末)如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP= t ;DP= 12﹣t ;BQ= 15﹣2t ;CQ= 2t .
(2)当t为何值时,四边形APQB是平行四边形?
(3)当t为何值时,四边形PDCQ是平行四边形?
【分析】(1)根据速度、路程以及时间的关系和线段之间的数量关系,即可求出AP,DP,BQ,CQ的长
(2)当AP=BQ时,四边形APQB是平行四边形,建立关于t的一元一次方程方程,解方程求出符合题意的t值即可;
(3)当PD=CQ时,四边形PDCQ是平行四边形;建立关于t的一元一次方程方程,解方程求出符合题意的t值即可.
【解答】解:(1)t,12﹣t,15﹣2t,2t
(2)根据题意有AP=t,CQ=2t,PD=12﹣t,BQ=15﹣2t.
∵AD∥BC,∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15﹣2t,解得t=5.
∴运动5s时四边形APQB是平行四边形;
(3)由AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,
∴PD=AD﹣AP=12﹣t,
如图1当PQ∥CD,且PQ=CD时,
∵AD∥BC,即PD∥QC,
∴四边形PQCD为平行四边形,
∴PQ=CD,PD=CQ,
∴12﹣t=2t,
解得t=4s,
即当t=4s时,四边形PDCQ是平行四边形.
9.(2015春 绿园区期末)如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从A向点D以1cm/s的速度运动,到点D即停止.点Q从点C向点B以2cm/s的速度运动,到点B即停止.直线PQ将四边形ABCD截得两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形?
【分析】①若四边形ABQP是平行四边形,则AP=BQ,进而求出t的值;②若四边形PQCD是平行四边形,则PD=CQ,进而求出t的值.
【解答】解:设当P,Q两点同时出发,t秒后,四边形ABQP或四边形PQCD是平行四边形,
根据题意可得:
AP=tcm,PD=(24﹣t)cm,CQ=2tcm,BQ=(30﹣2t)cm,
①若四边形ABQP是平行四边形,
则AP=BQ,
∴t=30﹣2t,
解得:t=10,
∴10s后四边形ABQP是平行四边形;
②若四边形PQCD是平行四边形,
则PD=CQ,
∴24﹣t=2t,
解得:t=8,
∴8s后四边形PQCD是平行四边形;
综上所述:当P,Q两点同时出发,8秒或10秒后,四边形ABQP或四边形PQCD是平行四边形.
10.(2015 杭州模拟)如图,平行四边形ABCD中,AC=6,BD=8,点P从点A出发以每秒1cm的速度沿射线AC移动,点Q从点C出发以每秒1cm的速度沿射线CA移动.
(1)经过几秒,以P,Q,B,D为顶点的四边形为矩形?
(2)若BC⊥AC垂足为C,求(1)中矩形边BQ的长.
【分析】(1)由四边形ABCD是平行四边形,AC=6,得到CP=AQ=1,PQ=BD=8,由OB=DO,OQ=OP,证得四边形BPDQ为平形四边形,根据对角线相等,证得四边形BPDQ为矩形;
(2)根据直角三角形的性质、勾股定理求得结论.
【解答】解:(1)当时间t=7秒时,四边形BPDQ为矩形.
理由如下:当t=7秒时,PA=QC=7,
∵AC=6,
∴CP=AQ=1
∴PQ=BD=8
∵四边形ABCD为平行四边形,BD=8
∴AO=CO=3
∴BO=DO=4
∴OQ=OP=4
∴四边形BPDQ为平形四边形,
∵PQ=BD=8
∴四边形BPDQ为矩形,
(2)由(1)得BO=4,CQ=7,
∵BC⊥AC
∴∠BCA=90°
BC2+CQ2=BQ2
∴BQ=.
11.(2015春 长清区期末)如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1cm/s的速度运动,点Q从C点开始沿CB边向B以2cm/s的速度运动,如果P、Q分别从A、C同时出发,设运动时间为t秒.
求:(1)当t为何值时,四边形ABQP为矩形?
(2)当t为何值时,四边形PQCD为平行四边形?
【分析】(1)四边形PQCD为矩形,即AP=BQ,列出等式,求解即可;
(2)四边形PQCD为平行四边形,即CQ=PD,列出等式求解;
【解答】解:(1)由题意知AP=t,CQ=2t,所以BQ=21﹣2t,
∵AD∥BC,
∴AP∥BQ,
又∵∠B=90°,
∴要使四边形ABQP为矩形,只需满足AP=BQ,
即:t=21﹣2t,
解得t=7,
∴当t=7s时,四边形ABQP为矩形;
(2)解:由题意知:AP=t,QC=2t,PD=18﹣t,当PT=QC时,四边形PACD为平形四边形,
即18﹣t=2t,
∴t=6,
∴当t=6时,四边形PQCD为平形四边形.
12.(2016 开江县二模)如图,在△ABD中,AB=AD,AO平分∠BAD,过点D作AB的平行线交AO的延长线于点C,连接BC.
(1)求证:四边形ABCD是菱形;
(2)如果OA,OB(OA>OB)的长(单位:米)是一元二次方程x2﹣7x+12=0的两根,求AB的长以及菱形ABCD的面积;
(3)若动点M从A出发,沿AC以2m/S的速度匀速直线运动到点C,动点N从B出发,沿BD以1m/S的速度匀速直线运动到点D,当M运动到C点时运动停止.若M、N同时出发,问出发几秒钟后,△MON的面积为?
【分析】(1)根据题意,用“一组对边平行且相等的四边形是平行四边形”先判定平行四边形,再用邻边相等证明菱形;
(2)解方程可得OA、OB的长,用勾股定理可求AB,根据“菱形的面积对应对角线积的一半”计算连线面积;
(3)根据点M、N运动过程中与O点的位置关系,分三种情况分别讨论.
【解答】(1)证明:∵AO平分∠BAD,AB∥CD
∴∠DAC=∠BAC=∠DCA
∴△ACD是等腰三角形,AD=DC
又∵AB=AD
∴AB=CD,
∴四边形ABCD为平行四边形,
又∵AB=AD,∴ ABCD是菱形;
(2)解:解方程x2﹣7x+12=0,得
OA=4,OB=3,
利用勾股定理AB==5,
S菱形ABCD=AC×BD=×8×6=24平方米.
(3)解:在第(2)问的条件下,设M、N同时出发x秒钟后,△MON的面积为,
当点M在OA上时,x≤2,S△MON=(4﹣2x)(3﹣x)=;
解得x1=,x2=(大于2,舍去);
当点M在OC上且点N在OB上时,2<x<3,S△MON=(3﹣x)(2x﹣4)=,
解得x1=x2=;
当点M在OC上且点N在OD上时,即3≤x≤4,S△MON=(2x﹣4)(x﹣3)=;
解得x1=,x2=(小于3,舍去).
综上所述:M,N出发秒,秒,秒钟后,△MON的面积为.
13.(2016春 丹阳市校级月考)如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点B出发,沿BA方向以每秒cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设Q点运动的时间t秒,若四边形QPBP′为菱形,求t的值多少秒?并说明理由.
【分析】根据等腰直角三角形的性质可得∠ABC=45°,再表示出BP、BQ,然后根据翻折的性质和菱形对角线互相垂直平分列出方程求解即可.
【解答】解:若四边形QPBP′为菱形,t=2秒;理由如下:
∵∠C=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,
∵点P的速度是每秒cm,点Q的速度是每秒1cm,
∴BP=tcm,BQ=(6﹣t)cm,
∵四边形QPBP′为菱形,
∴t×=,
解得:t=2;
即若四边形QPBP′为菱形,t的值为2秒.
14.(2016春 江阴市校级月考)如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=16cm,BC=22cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒.
(1)当t为多少时,四边形ABQP成为矩形?
(2)四边形PBQD是否能成为菱形?若能,求出t的值;若不能,请说明理由,并探究如何改变Q点的速度(匀速运动),使四边形PBQD在某一时刻为菱形,求点Q的速度.
【分析】(1)因为∠B=90°,AP∥BQ,由矩形的判定可知当AP=BQ时,四边形ABQP成为矩形;
(2)因为PD∥BQ,当PD=BQ=BP时,四边形PBQD能成为菱形,先由PD=BQ求出运动时间t的值,再代入求BP,发现BP≠PD,判断此时四边形PBQD不能成为菱形;设Q点的速度改变为vcm/s时,四边形PBQD在时刻t为菱形,根据PD=BQ=BP列出关于v、t的方程组,解方程组即可求出点Q的速度.
【解答】解:(1)∵∠B=90°,AP∥BQ,
∴当AP=BQ时,四边形ABQP成为矩形,
此时有t=22﹣3t,解得t=.
∴当t=s时,四边形ABQP成为矩形;
(2)四边形PBQD不能成为菱形.理由如下:
∵PD∥BQ,
∴当PD=BQ=BP时,四边形PBQD能成为菱形.
由PD=BQ,得16﹣t=22﹣3t,解得t=3,
当t=3时,PD=BQ=13,BP====≠13,
∴四边形PBQD不能成为菱形;
如果Q点的速度改变为vcm/s时,能够使四边形PBQD在时刻ts为菱形,
由题意,得,解得.
故点Q的速度为2cm/s时,能够使四边形PBQD在某一时刻为菱形.
15.(2015 元阳县校级一模)如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,点P从点A出发,以1cm/s的速度向点D运动(不与D重合).设点P运动的时间为t秒,请用t表示PD的长;
(3)当t为何值时,四边形PBQD是菱形?
【分析】(1)由矩形ABCD中,O为BD的中点,易证得△PDO≌△QBO(ASA),继而证得OP=OQ;
(2)AD=8cm,AP=tcm,即可用t表示PD的长;
(3)由四边形PBQD是菱形,可得PB=PD,即可得AB2+AP2=PD2,继而可得方程62+t2=(8﹣t)2,解此方程即可求得答案.
【解答】解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,
∵O为BD的中点,
∴DO=BO,
在△PDO和△QBO中,
,
∴△PDO≌△QBO(ASA),
∴OP=OQ;
(2)由题意知:AD=8cm,AP=tcm,
∴PD=8﹣t,
(3)∵PB=PD,
∴PB2=PD2,
即AB2+AP2=PD2,
∴62+t2=(8﹣t)2,
解得
t=,
∴当t=时,PB=PD.
16.(2015 郑州校级三模)如图,在△ABC中,AB=AC=10cm,BC=12cm,E是BA延长线的一点.
(1)利用尺规∠EAC的平分线AD(保留作图痕迹,不写作法);
(2)若点P在射线AD上从点A开始运动,点Q在线段CB上从点C向点点B运动,运动的速度均为1cm/s,运动时间为t,若P、Q同时运动.
①连接PQ交AC于点O.求证:AO=CO;
②填空:当t= 6 秒时四边形APCQ一定是矩形;
③填空:当t= 秒时四边形APCQ一定是菱形.
【分析】(1)利用尺规作图作出已知角的平分线即可;
(2)根据平行四边形的性质、矩形的性质及菱形的性质分别求得t的值即可.
【解答】解:(1)作图如下:
(2)①∵AP平分∠EAC,∠EAC=2∠B=2∠C,
∴∠PAC=∠C,
∴AP∥BC,
∵点P和点Q的速度均为1cm/s,
∴AP=CQ,
∴AO=CO;
②∵当∠AQC=90°时,四边形AQCP为矩形,
此时AQ⊥BC,CQ=BC=6,
∴当t=6时,四边形AQCP为矩形;
③如图3:当四边形APCQ是菱形时,AQ=CQ,
作AD⊥CQ于点D,
则CD=BC=6,
CQ=AQ=t,QD=t﹣6,
在Rt△AQD中,
AQ2=QD2+AD2,
即:t2=(t﹣6)2+82,
解得:t=,
∴当t=时,四边形AQCP为菱形.
17.(2015春 江西期末)如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以lcm/s的速度运动,同时点F从点B出发沿线射BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)当t为多少时,四边形ACFE是菱形.
【分析】(1)由题意得到AD=CD,再由AG与BC平行,利用两直线平行内错角相等得到两对角相等,利用AAS即可得证;
(2)若四边形ACFE是菱形,则有CF=AC=AE=6,由E的速度求出E运动的时间即可.
【解答】(1)证明:∵AG∥BC,
∴∠EAD=∠DCF,∠AED=∠DFC,
∵D为AC的中点,
∴AD=CD,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS);
(2)解:①若四边形ACFE是菱形,则有CF=AC=AE=6,
则此时的时间t=6÷1=6(s).
故答案为:6s.
18.(2015春 日照期末)如图,矩形ABCD中,对角线AC、BD相交于点O,点P是线段AD上一动点(不与与点D重合),PO的延长线交BC于Q点.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=6cm,AD=8cm,P从点A出发.以1cm/秒的速度向点D匀速运动.设点P运动时间为t秒,问四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
【分析】(1)依据矩形的性质和平行线的性质,通过全等三角形的判定定理判定△POD≌△QOB,所以OP=OQ,则四边形PBQD的对角线互相平分,故四边形PBQD为平行四边形.
(2)点P从点A出发运动t秒时,AP=tcm,PD=(4﹣t)cm.当四边形PBQD是菱形时,PB=PD=(4﹣t)cm.在直角△ABP中,根据勾股定理得到AP2+AB2=PB2,即t2+32=(4﹣t)2,由此可以求得t的值.
【解答】(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,
在△POD和△QOB中,
,
∴△POD≌△QOB(ASA),
∴OP=OQ;
又∵OB=OD
∴四边形PBQD为平行四边形;
(2)答:能成为菱形;
证明:t秒后AP=t,PD=8﹣t,
若四边形PBQD是菱形,
∴PD=BP=8﹣t,
∵四边形ABCD是矩形,
∴∠A=90°,
在Rt△ABP中,由勾股定理得:AB2+AP2=BP2,
即62+t2=(8﹣t)2,
解得:t=.
即点P运动时间为秒时,四边形PBQD是菱形.
19.(2014春 兴业县期末)如图,已知△ABC和△DEF是两个边长为10cm的等边三角形,且B、D、C、E都在同一直线上.连接AD、CF.
(1)求证:四边形ADFC是平行四边形;
(2)若BD=4cm,△ABC沿着BE的方向以每秒2cm的速度运动,设△ABC运动时间为t秒,当t为何值时, ADFC是菱形?请说明你的理由.
【分析】(1)因为△ABC和△DEF是两个边长为10cm的等边三角形所以AC=DF,又由∠ACD=∠FDE=60°,可得AC∥DF,所以四边形ADFC是平行四边形;
(2)根据△ABC沿着BE的方向以每秒1cm的速度运动,所以当t==2秒时,B与D重合,这时四边形为菱形.
【解答】(1)证明:∵△ABC和△DEF是两个边长为10cm的等边三角形.
∴AC=DF,∠ACD=∠FDE=60°,
∴AC∥DF,
∴四边形ADFC是平行四边形;
(2)解:当t=2秒时,平行四边形ADFC是菱形,理由如下:
∵△ABC沿着BE的方向以每秒1cm的速度运动,
∴当t==2秒时,B与D重合,如图所示,
则AD=AE=BC=DE=DF=EF,
∴平行四边形ADFC是菱形;
一.解答题(共19小题)
1.(2016 宝应县一模)某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.6万元,设可变成本平均每年增长的百分率为x.
(1)用含x的代数式表示第3年的可变成本为 万元;
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年增长的百分率x.
2.(2016 临沭县校级一模)某企业2010年盈利1500万元,2012年克服全球金融危机的不利影响,仍实现盈利2160万元.从2010年到2012年,如果该企业每年盈利的年增长率相同,求:
(1)该企业2011年盈利多少万元?
(2)若该企业盈利的年增长率继续保持不变,预计2013年盈利多少万元?
3.(2016 安徽四模)随着市民环保意识的增强,烟花爆竹销售量逐年下降.常德市2012年销售烟花爆竹20万箱,到2014年烟花爆竹销售量为9.8万箱.求常德市2012年到2014年烟花爆竹年销售量的平均下降率.
4.(2016 景德镇校级二模)某地区2014年投入教育经费1000万元,至2016年三年总计投入教育经费3640万元,假设2014年至2016年该地区投入教育经费的平均增长率相同,根据这个年平均增长率,预计2017年该地区将投入教育经费多少万元?
5.(2015 柳州)如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=12cm,BC=18cm,点P从点A出发以2cm/s的速度沿A→D→C运动,点P从点A出发的同时点Q从点C出发,以1cm/s的速度向点B运动,当点P到达点C时,点Q也停止运动.设点P,Q运动的时间为t秒.
(1)从运动开始,当t取何值时,PQ∥CD?
(2)从运动开始,当t取何值时,△PQC为直角三角形?
6.(2015 昌邑市校级模拟)如图,在平面直角坐标系中,点A,B的坐标分别是(﹣3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造□PCOD.在线段OP延长线上一动点E,且满足PE=AO.
(1)当点C在线段OB上运动时,求证:四边形ADEC为平行四边形;
(2)当点P运动的时间为秒时,求此时四边形ADEC的周长是多少?
7.(2015 河南模拟)如图,△ABC中AB=AC,点D从点B出发沿射线BA移动,同时,点E从点C出发沿线段AC的延长线移动,已点知D、E移动的速度相同,DE与直线BC相交于点F.
(1)如图1,当点D在线段AB上时,过点D作AC的平行线交BC于点G,连接CD、GE,判定四边形CDGE的形状,并证明你的结论;
(2)过点D作直线BC的垂线垂足为M,当点D、E在移动的过程中,线段BM、MF、CF有何数量关系?请直接写出你的结论.
8.(2015春 山亭区期末)如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP= ;DP= ;BQ= ;CQ= .
(2)当t为何值时,四边形APQB是平行四边形?
(3)当t为何值时,四边形PDCQ是平行四边形?
9.(2015春 绿园区期末)如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从A向点D以1cm/s的速度运动,到点D即停止.点Q从点C向点B以2cm/s的速度运动,到点B即停止.直线PQ将四边形ABCD截得两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形?
10.(2015 杭州模拟)如图,平行四边形ABCD中,AC=6,BD=8,点P从点A出发以每秒1cm的速度沿射线AC移动,点Q从点C出发以每秒1cm的速度沿射线CA移动.
(1)经过几秒,以P,Q,B,D为顶点的四边形为矩形?
(2)若BC⊥AC垂足为C,求(1)中矩形边BQ的长.
11.(2015春 长清区期末)如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1cm/s的速度运动,点Q从C点开始沿CB边向B以2cm/s的速度运动,如果P、Q分别从A、C同时出发,设运动时间为t秒.
求:(1)当t为何值时,四边形ABQP为矩形?
(2)当t为何值时,四边形PQCD为平行四边形?
12.(2016 开江县二模)如图,在△ABD中,AB=AD,AO平分∠BAD,过点D作AB的平行线交AO的延长线于点C,连接BC.
(1)求证:四边形ABCD是菱形;
(2)如果OA,OB(OA>OB)的长(单位:米)是一元二次方程x2﹣7x+12=0的两根,求AB的长以及菱形ABCD的面积;
(3)若动点M从A出发,沿AC以2m/S的速度匀速直线运动到点C,动点N从B出发,沿BD以1m/S的速度匀速直线运动到点D,当M运动到C点时运动停止.若M、N同时出发,问出发几秒钟后,△MON的面积为?
13.(2016春 丹阳市校级月考)如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点B出发,沿BA方向以每秒cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设Q点运动的时间t秒,若四边形QPBP′为菱形,求t的值多少秒?并说明理由.
14.(2016春 江阴市校级月考)如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=16cm,BC=22cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒.
(1)当t为多少时,四边形ABQP成为矩形?
(2)四边形PBQD是否能成为菱形?若能,求出t的值;若不能,请说明理由,并探究如何改变Q点的速度(匀速运动),使四边形PBQD在某一时刻为菱形,求点Q的速度.
15.(2015 元阳县校级一模)如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,点P从点A出发,以1cm/s的速度向点D运动(不与D重合).设点P运动的时间为t秒,请用t表示PD的长;
(3)当t为何值时,四边形PBQD是菱形?
16.(2015 郑州校级三模)如图,在△ABC中,AB=AC=10cm,BC=12cm,E是BA延长线的一点.
(1)利用尺规∠EAC的平分线AD(保留作图痕迹,不写作法);
(2)若点P在射线AD上从点A开始运动,点Q在线段CB上从点C向点点B运动,运动的速度均为1cm/s,运动时间为t,若P、Q同时运动.
①连接PQ交AC于点O.求证:AO=CO;
②填空:当t= 秒时四边形APCQ一定是矩形;
③填空:当t= 秒时四边形APCQ一定是菱形.
17.(2015春 江西期末)如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以lcm/s的速度运动,同时点F从点B出发沿线射BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)当t为多少时,四边形ACFE是菱形.
18.(2015春 日照期末)如图,矩形ABCD中,对角线AC、BD相交于点O,点P是线段AD上一动点(不与与点D重合),PO的延长线交BC于Q点.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=6cm,AD=8cm,P从点A出发.以1cm/秒的速度向点D匀速运动.设点P运动时间为t秒,问四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
19.(2014春 兴业县期末)如图,已知△ABC和△DEF是两个边长为10cm的等边三角形,且B、D、C、E都在同一直线上.连接AD、CF.
(1)求证:四边形ADFC是平行四边形;
(2)若BD=4cm,△ABC沿着BE的方向以每秒2cm的速度运动,设△ABC运动时间为t秒,当t为何值时, ADFC是菱形?请说明你的理由.
增长率问题和四边形中的动点问题20160610
参考答案与试题解析
一.解答题(共19小题)
1.(2016 宝应县一模)某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.6万元,设可变成本平均每年增长的百分率为x.
(1)用含x的代数式表示第3年的可变成本为 2.6(1+x)2 万元;
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年增长的百分率x.
【分析】(1)根据增长率问题由第1年的可变成本为2.6万元就可以表示出第二年的可变成本为2.6(1+x),则第三年的可变成本为2.6(1+x)2,故得出答案;
(2)根据养殖成本=固定成本+可变成本建立方程求出其解即可
【解答】解:(1)由题意,得
第3年的可变成本为:2.6(1+x)2,
故答案为:2.6(1+x)2;
(2)由题意,得
4+2.6(1+x)2=7.146,
解得:x1=0.1,x2=﹣2.1(不合题意,舍去).
答:可变成本平均每年增长的百分率为10%.
2.(2016 临沭县校级一模)某企业2010年盈利1500万元,2012年克服全球金融危机的不利影响,仍实现盈利2160万元.从2010年到2012年,如果该企业每年盈利的年增长率相同,求:
(1)该企业2011年盈利多少万元?
(2)若该企业盈利的年增长率继续保持不变,预计2013年盈利多少万元?
【分析】(1)设每年盈利的年增长率为x,就可以表示出2012年的盈利,根据2012年的盈利为2160万元建立方程求出x的值就可以求出2011年的盈利;
(2)根据(1)求出的年增长率就可以求出结论.
【解答】(1)设每年盈利的年增长率为x,根据意,得
1500(1+x)2=2160
解得:x1=0.2,x2=﹣2.2(不合题意,舍去)
∴该企业2011年盈利为:1500(1+0.2)=1800万元.
答:2011年该企业盈利1800万元;
(2)由题意,得
2160(1+0.2)=2592万元
答:预计2013年该企业盈利2592万元.
3.(2016 安徽四模)随着市民环保意识的增强,烟花爆竹销售量逐年下降.常德市2012年销售烟花爆竹20万箱,到2014年烟花爆竹销售量为9.8万箱.求常德市2012年到2014年烟花爆竹年销售量的平均下降率.
【分析】先设常德市2012年到2014年烟花爆竹年销售量的平均下降率是x,那么把2012年的烟花爆竹销售量看做单位1,在此基础上可求2013年的年销售量,以此类推可求2014年的年销售量,而2014年烟花爆竹销售量为9.8万箱,据此可列方程,解即可.
【解答】解:设常德市2012年到2014年烟花爆竹年销售量的平均下降率是x,依题意得
20(1﹣x)2=9.8,
解这个方程,得x1=0.3,x2=1.7,
由于x2=1.7不符合题意,即x=0.3=30%.
答:常德市2012年到2014年烟花爆竹年销售量的平均下降率为30%.
4.(2016 景德镇校级二模)某地区2014年投入教育经费1000万元,至2016年三年总计投入教育经费3640万元,假设2014年至2016年该地区投入教育经费的平均增长率相同,根据这个年平均增长率,预计2017年该地区将投入教育经费多少万元?
【分析】一般用增长后的量=增长前的量×(1+增长率),2015年要投入教育经费是1000(1+x)万元,在2016年的基础上再增长x,就是2016年的教育经费数额,即可列出方程求解.利用求得的增长率来求2017年该地区将投入教育经费.
【解答】解:设增长率为x,根据题意可得:1000+1000(1+x)+1000(1+x)2=3640,
化简得:25x2+75x﹣16=0,
解得:(舍去),
所以2016年该地区投入教育经费为,
根据所得的年平均增长率,预计2017年该地区将投入教育经费为1440×1.2=1728万元.
答:2017年该地区将投入教育经费1728万元.
5.(2015 柳州)如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=12cm,BC=18cm,点P从点A出发以2cm/s的速度沿A→D→C运动,点P从点A出发的同时点Q从点C出发,以1cm/s的速度向点B运动,当点P到达点C时,点Q也停止运动.设点P,Q运动的时间为t秒.
(1)从运动开始,当t取何值时,PQ∥CD?
(2)从运动开始,当t取何值时,△PQC为直角三角形?
【分析】(1)已知AD∥BC,添加PD=CQ即可判断以PQDC为顶点的四边形是平行四边形.
(2)点P处可能为直角,点Q处也可能是直角,而后求解即可.
【解答】解:(1)当PQ∥CD时,四边形PDCB是平行四边形,
此时PD=QC,
∴12﹣2t=t,
∴t=4.
∴当t=4时,四边形PQDC是平行四边形.
(2)过D点,DF⊥BC于F,
∴DF=AB=8.
FC=BC﹣AD=18﹣12=6,CD=10,
①当PQ⊥BC,
则BQ+CQ=18.即:2t+t=18,
∴t=6;
②当QP⊥PC,此时P一定在DC上,
CP1=10+12﹣2t=22﹣2t,CQ2=t,
易知,△CDF∽△CQ2P1,
∴,
解得:t=,
③情形:当PC⊥BC时,因∠DCB<90°,此种情形不存在.
∴当t=6或时,△PQC是直角三角形.
6.(2015 昌邑市校级模拟)如图,在平面直角坐标系中,点A,B的坐标分别是(﹣3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造□PCOD.在线段OP延长线上一动点E,且满足PE=AO.
(1)当点C在线段OB上运动时,求证:四边形ADEC为平行四边形;
(2)当点P运动的时间为秒时,求此时四边形ADEC的周长是多少?
【分析】(1)连接CD交AE于F,根据平行四边形的性质得到CF=DP,OF=PF,根据题意得到AF=EF,又CF=DP,根据平行四边形的判定定理证明即可;
(2)根据题意计算出OC、OP的长,根据勾股定理求出AC、CE,根据平行四边形的周长公式计算即可.
【解答】(1)证明:连接CD交AE于F,
∵四边形PCOD是平行四边形,
∴CF=DF,OF=PF,
∵PE=AO,
∴AF=EF,又CF=DP,
∴四边形ADEC为平行四边形;
(2)解:当点P运动的时间为秒时,OP=,OC=3,
则OE=,
由勾股定理得,AC==3,
CE==,
∵四边形ADEC为平行四边形,
∴周长为(3+)×2=6+.
7.(2015 河南模拟)如图,△ABC中AB=AC,点D从点B出发沿射线BA移动,同时,点E从点C出发沿线段AC的延长线移动,已点知D、E移动的速度相同,DE与直线BC相交于点F.
(1)如图1,当点D在线段AB上时,过点D作AC的平行线交BC于点G,连接CD、GE,判定四边形CDGE的形状,并证明你的结论;
(2)过点D作直线BC的垂线垂足为M,当点D、E在移动的过程中,线段BM、MF、CF有何数量关系?请直接写出你的结论.
【分析】(1)由题意得出BD=CE,由平行线的性质得出∠DGB=∠ACB,由等腰三角形的性质得出∠B=∠ACB,得出∠B=∠DGB,证出BD=GD=CE,即可得出结论;
(2)由(1)得:BD=GD=CE,由等腰三角形的三线合一性质得出BM=GM,由平行线得出GF=CF,即可得出结论.
【解答】解:(1)四边形CDGE是平行四边.理由如下:如图1所示:
∵D、E移动的速度相同,
∴BD=CE,
∵DG∥AE,
∴∠DGB=∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠DGB,
∴BD=GD=CE,
又∵DG∥CE,
∴四边形CDGE是平行四边形;
(2)BM+CF=MF;理由如下:如图2所示:
由(1)得:BD=GD=CE,
∵DM⊥BC,
∴BM=GM,
∵DG∥AE,
∴GF=CF,
∴BM+CF=GM+GF=MF.
8.(2015春 山亭区期末)如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP= t ;DP= 12﹣t ;BQ= 15﹣2t ;CQ= 2t .
(2)当t为何值时,四边形APQB是平行四边形?
(3)当t为何值时,四边形PDCQ是平行四边形?
【分析】(1)根据速度、路程以及时间的关系和线段之间的数量关系,即可求出AP,DP,BQ,CQ的长
(2)当AP=BQ时,四边形APQB是平行四边形,建立关于t的一元一次方程方程,解方程求出符合题意的t值即可;
(3)当PD=CQ时,四边形PDCQ是平行四边形;建立关于t的一元一次方程方程,解方程求出符合题意的t值即可.
【解答】解:(1)t,12﹣t,15﹣2t,2t
(2)根据题意有AP=t,CQ=2t,PD=12﹣t,BQ=15﹣2t.
∵AD∥BC,∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15﹣2t,解得t=5.
∴运动5s时四边形APQB是平行四边形;
(3)由AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,
∴PD=AD﹣AP=12﹣t,
如图1当PQ∥CD,且PQ=CD时,
∵AD∥BC,即PD∥QC,
∴四边形PQCD为平行四边形,
∴PQ=CD,PD=CQ,
∴12﹣t=2t,
解得t=4s,
即当t=4s时,四边形PDCQ是平行四边形.
9.(2015春 绿园区期末)如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从A向点D以1cm/s的速度运动,到点D即停止.点Q从点C向点B以2cm/s的速度运动,到点B即停止.直线PQ将四边形ABCD截得两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形?
【分析】①若四边形ABQP是平行四边形,则AP=BQ,进而求出t的值;②若四边形PQCD是平行四边形,则PD=CQ,进而求出t的值.
【解答】解:设当P,Q两点同时出发,t秒后,四边形ABQP或四边形PQCD是平行四边形,
根据题意可得:
AP=tcm,PD=(24﹣t)cm,CQ=2tcm,BQ=(30﹣2t)cm,
①若四边形ABQP是平行四边形,
则AP=BQ,
∴t=30﹣2t,
解得:t=10,
∴10s后四边形ABQP是平行四边形;
②若四边形PQCD是平行四边形,
则PD=CQ,
∴24﹣t=2t,
解得:t=8,
∴8s后四边形PQCD是平行四边形;
综上所述:当P,Q两点同时出发,8秒或10秒后,四边形ABQP或四边形PQCD是平行四边形.
10.(2015 杭州模拟)如图,平行四边形ABCD中,AC=6,BD=8,点P从点A出发以每秒1cm的速度沿射线AC移动,点Q从点C出发以每秒1cm的速度沿射线CA移动.
(1)经过几秒,以P,Q,B,D为顶点的四边形为矩形?
(2)若BC⊥AC垂足为C,求(1)中矩形边BQ的长.
【分析】(1)由四边形ABCD是平行四边形,AC=6,得到CP=AQ=1,PQ=BD=8,由OB=DO,OQ=OP,证得四边形BPDQ为平形四边形,根据对角线相等,证得四边形BPDQ为矩形;
(2)根据直角三角形的性质、勾股定理求得结论.
【解答】解:(1)当时间t=7秒时,四边形BPDQ为矩形.
理由如下:当t=7秒时,PA=QC=7,
∵AC=6,
∴CP=AQ=1
∴PQ=BD=8
∵四边形ABCD为平行四边形,BD=8
∴AO=CO=3
∴BO=DO=4
∴OQ=OP=4
∴四边形BPDQ为平形四边形,
∵PQ=BD=8
∴四边形BPDQ为矩形,
(2)由(1)得BO=4,CQ=7,
∵BC⊥AC
∴∠BCA=90°
BC2+CQ2=BQ2
∴BQ=.
11.(2015春 长清区期末)如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1cm/s的速度运动,点Q从C点开始沿CB边向B以2cm/s的速度运动,如果P、Q分别从A、C同时出发,设运动时间为t秒.
求:(1)当t为何值时,四边形ABQP为矩形?
(2)当t为何值时,四边形PQCD为平行四边形?
【分析】(1)四边形PQCD为矩形,即AP=BQ,列出等式,求解即可;
(2)四边形PQCD为平行四边形,即CQ=PD,列出等式求解;
【解答】解:(1)由题意知AP=t,CQ=2t,所以BQ=21﹣2t,
∵AD∥BC,
∴AP∥BQ,
又∵∠B=90°,
∴要使四边形ABQP为矩形,只需满足AP=BQ,
即:t=21﹣2t,
解得t=7,
∴当t=7s时,四边形ABQP为矩形;
(2)解:由题意知:AP=t,QC=2t,PD=18﹣t,当PT=QC时,四边形PACD为平形四边形,
即18﹣t=2t,
∴t=6,
∴当t=6时,四边形PQCD为平形四边形.
12.(2016 开江县二模)如图,在△ABD中,AB=AD,AO平分∠BAD,过点D作AB的平行线交AO的延长线于点C,连接BC.
(1)求证:四边形ABCD是菱形;
(2)如果OA,OB(OA>OB)的长(单位:米)是一元二次方程x2﹣7x+12=0的两根,求AB的长以及菱形ABCD的面积;
(3)若动点M从A出发,沿AC以2m/S的速度匀速直线运动到点C,动点N从B出发,沿BD以1m/S的速度匀速直线运动到点D,当M运动到C点时运动停止.若M、N同时出发,问出发几秒钟后,△MON的面积为?
【分析】(1)根据题意,用“一组对边平行且相等的四边形是平行四边形”先判定平行四边形,再用邻边相等证明菱形;
(2)解方程可得OA、OB的长,用勾股定理可求AB,根据“菱形的面积对应对角线积的一半”计算连线面积;
(3)根据点M、N运动过程中与O点的位置关系,分三种情况分别讨论.
【解答】(1)证明:∵AO平分∠BAD,AB∥CD
∴∠DAC=∠BAC=∠DCA
∴△ACD是等腰三角形,AD=DC
又∵AB=AD
∴AB=CD,
∴四边形ABCD为平行四边形,
又∵AB=AD,∴ ABCD是菱形;
(2)解:解方程x2﹣7x+12=0,得
OA=4,OB=3,
利用勾股定理AB==5,
S菱形ABCD=AC×BD=×8×6=24平方米.
(3)解:在第(2)问的条件下,设M、N同时出发x秒钟后,△MON的面积为,
当点M在OA上时,x≤2,S△MON=(4﹣2x)(3﹣x)=;
解得x1=,x2=(大于2,舍去);
当点M在OC上且点N在OB上时,2<x<3,S△MON=(3﹣x)(2x﹣4)=,
解得x1=x2=;
当点M在OC上且点N在OD上时,即3≤x≤4,S△MON=(2x﹣4)(x﹣3)=;
解得x1=,x2=(小于3,舍去).
综上所述:M,N出发秒,秒,秒钟后,△MON的面积为.
13.(2016春 丹阳市校级月考)如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点B出发,沿BA方向以每秒cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设Q点运动的时间t秒,若四边形QPBP′为菱形,求t的值多少秒?并说明理由.
【分析】根据等腰直角三角形的性质可得∠ABC=45°,再表示出BP、BQ,然后根据翻折的性质和菱形对角线互相垂直平分列出方程求解即可.
【解答】解:若四边形QPBP′为菱形,t=2秒;理由如下:
∵∠C=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,
∵点P的速度是每秒cm,点Q的速度是每秒1cm,
∴BP=tcm,BQ=(6﹣t)cm,
∵四边形QPBP′为菱形,
∴t×=,
解得:t=2;
即若四边形QPBP′为菱形,t的值为2秒.
14.(2016春 江阴市校级月考)如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=16cm,BC=22cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒.
(1)当t为多少时,四边形ABQP成为矩形?
(2)四边形PBQD是否能成为菱形?若能,求出t的值;若不能,请说明理由,并探究如何改变Q点的速度(匀速运动),使四边形PBQD在某一时刻为菱形,求点Q的速度.
【分析】(1)因为∠B=90°,AP∥BQ,由矩形的判定可知当AP=BQ时,四边形ABQP成为矩形;
(2)因为PD∥BQ,当PD=BQ=BP时,四边形PBQD能成为菱形,先由PD=BQ求出运动时间t的值,再代入求BP,发现BP≠PD,判断此时四边形PBQD不能成为菱形;设Q点的速度改变为vcm/s时,四边形PBQD在时刻t为菱形,根据PD=BQ=BP列出关于v、t的方程组,解方程组即可求出点Q的速度.
【解答】解:(1)∵∠B=90°,AP∥BQ,
∴当AP=BQ时,四边形ABQP成为矩形,
此时有t=22﹣3t,解得t=.
∴当t=s时,四边形ABQP成为矩形;
(2)四边形PBQD不能成为菱形.理由如下:
∵PD∥BQ,
∴当PD=BQ=BP时,四边形PBQD能成为菱形.
由PD=BQ,得16﹣t=22﹣3t,解得t=3,
当t=3时,PD=BQ=13,BP====≠13,
∴四边形PBQD不能成为菱形;
如果Q点的速度改变为vcm/s时,能够使四边形PBQD在时刻ts为菱形,
由题意,得,解得.
故点Q的速度为2cm/s时,能够使四边形PBQD在某一时刻为菱形.
15.(2015 元阳县校级一模)如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,点P从点A出发,以1cm/s的速度向点D运动(不与D重合).设点P运动的时间为t秒,请用t表示PD的长;
(3)当t为何值时,四边形PBQD是菱形?
【分析】(1)由矩形ABCD中,O为BD的中点,易证得△PDO≌△QBO(ASA),继而证得OP=OQ;
(2)AD=8cm,AP=tcm,即可用t表示PD的长;
(3)由四边形PBQD是菱形,可得PB=PD,即可得AB2+AP2=PD2,继而可得方程62+t2=(8﹣t)2,解此方程即可求得答案.
【解答】解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,
∵O为BD的中点,
∴DO=BO,
在△PDO和△QBO中,
,
∴△PDO≌△QBO(ASA),
∴OP=OQ;
(2)由题意知:AD=8cm,AP=tcm,
∴PD=8﹣t,
(3)∵PB=PD,
∴PB2=PD2,
即AB2+AP2=PD2,
∴62+t2=(8﹣t)2,
解得
t=,
∴当t=时,PB=PD.
16.(2015 郑州校级三模)如图,在△ABC中,AB=AC=10cm,BC=12cm,E是BA延长线的一点.
(1)利用尺规∠EAC的平分线AD(保留作图痕迹,不写作法);
(2)若点P在射线AD上从点A开始运动,点Q在线段CB上从点C向点点B运动,运动的速度均为1cm/s,运动时间为t,若P、Q同时运动.
①连接PQ交AC于点O.求证:AO=CO;
②填空:当t= 6 秒时四边形APCQ一定是矩形;
③填空:当t= 秒时四边形APCQ一定是菱形.
【分析】(1)利用尺规作图作出已知角的平分线即可;
(2)根据平行四边形的性质、矩形的性质及菱形的性质分别求得t的值即可.
【解答】解:(1)作图如下:
(2)①∵AP平分∠EAC,∠EAC=2∠B=2∠C,
∴∠PAC=∠C,
∴AP∥BC,
∵点P和点Q的速度均为1cm/s,
∴AP=CQ,
∴AO=CO;
②∵当∠AQC=90°时,四边形AQCP为矩形,
此时AQ⊥BC,CQ=BC=6,
∴当t=6时,四边形AQCP为矩形;
③如图3:当四边形APCQ是菱形时,AQ=CQ,
作AD⊥CQ于点D,
则CD=BC=6,
CQ=AQ=t,QD=t﹣6,
在Rt△AQD中,
AQ2=QD2+AD2,
即:t2=(t﹣6)2+82,
解得:t=,
∴当t=时,四边形AQCP为菱形.
17.(2015春 江西期末)如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以lcm/s的速度运动,同时点F从点B出发沿线射BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)当t为多少时,四边形ACFE是菱形.
【分析】(1)由题意得到AD=CD,再由AG与BC平行,利用两直线平行内错角相等得到两对角相等,利用AAS即可得证;
(2)若四边形ACFE是菱形,则有CF=AC=AE=6,由E的速度求出E运动的时间即可.
【解答】(1)证明:∵AG∥BC,
∴∠EAD=∠DCF,∠AED=∠DFC,
∵D为AC的中点,
∴AD=CD,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS);
(2)解:①若四边形ACFE是菱形,则有CF=AC=AE=6,
则此时的时间t=6÷1=6(s).
故答案为:6s.
18.(2015春 日照期末)如图,矩形ABCD中,对角线AC、BD相交于点O,点P是线段AD上一动点(不与与点D重合),PO的延长线交BC于Q点.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=6cm,AD=8cm,P从点A出发.以1cm/秒的速度向点D匀速运动.设点P运动时间为t秒,问四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
【分析】(1)依据矩形的性质和平行线的性质,通过全等三角形的判定定理判定△POD≌△QOB,所以OP=OQ,则四边形PBQD的对角线互相平分,故四边形PBQD为平行四边形.
(2)点P从点A出发运动t秒时,AP=tcm,PD=(4﹣t)cm.当四边形PBQD是菱形时,PB=PD=(4﹣t)cm.在直角△ABP中,根据勾股定理得到AP2+AB2=PB2,即t2+32=(4﹣t)2,由此可以求得t的值.
【解答】(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,
在△POD和△QOB中,
,
∴△POD≌△QOB(ASA),
∴OP=OQ;
又∵OB=OD
∴四边形PBQD为平行四边形;
(2)答:能成为菱形;
证明:t秒后AP=t,PD=8﹣t,
若四边形PBQD是菱形,
∴PD=BP=8﹣t,
∵四边形ABCD是矩形,
∴∠A=90°,
在Rt△ABP中,由勾股定理得:AB2+AP2=BP2,
即62+t2=(8﹣t)2,
解得:t=.
即点P运动时间为秒时,四边形PBQD是菱形.
19.(2014春 兴业县期末)如图,已知△ABC和△DEF是两个边长为10cm的等边三角形,且B、D、C、E都在同一直线上.连接AD、CF.
(1)求证:四边形ADFC是平行四边形;
(2)若BD=4cm,△ABC沿着BE的方向以每秒2cm的速度运动,设△ABC运动时间为t秒,当t为何值时, ADFC是菱形?请说明你的理由.
【分析】(1)因为△ABC和△DEF是两个边长为10cm的等边三角形所以AC=DF,又由∠ACD=∠FDE=60°,可得AC∥DF,所以四边形ADFC是平行四边形;
(2)根据△ABC沿着BE的方向以每秒1cm的速度运动,所以当t==2秒时,B与D重合,这时四边形为菱形.
【解答】(1)证明:∵△ABC和△DEF是两个边长为10cm的等边三角形.
∴AC=DF,∠ACD=∠FDE=60°,
∴AC∥DF,
∴四边形ADFC是平行四边形;
(2)解:当t=2秒时,平行四边形ADFC是菱形,理由如下:
∵△ABC沿着BE的方向以每秒1cm的速度运动,
∴当t==2秒时,B与D重合,如图所示,
则AD=AE=BC=DE=DF=EF,
∴平行四边形ADFC是菱形;
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
