3.1圆的概念练习题(解析版)
图片预览



文档简介
圆的概念练习题20160922
一.选择题(共10小题)
1.下列命题正确的个数有( )
①过两点可以作无数个圆;
②经过三点一定可以作圆;
③任意一个三角形有一个外接圆,而且只有一个外接圆;
④任意一个圆有且只有一个内接三角形.
A.1个
B.2个
C.3个
D.4个
2.下列说法正确的是( )
A.一个点可以确定一条直线
B.两个点可以确定两条直线
C.三个点可以确定一个圆
D.不在同一直线上的三点确定一个圆
3.有下列四个命题,其中正确的有( )
①圆的对称轴是直径;
②经过三个点一定可以作圆;
③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.
A.4个
B.3个
C.2个
D.1个
4.过圆上一点可以作出圆的最长弦的条数为( )
A.1条
B.2条
C.3条
D.无数条
5.⊙O的半径r=5cm,圆心到直线l的距离OM=4cm,在直线l上有一点P,且PM=3cm,则点P( )
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.可能在⊙O上或在⊙O内
6.⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是( )
A.点P在⊙O内
B.点P的⊙O上
C.点P在⊙O外
D.点P在⊙O上或⊙O外
7.圆心在坐标原点,其半径为7的圆,则下列各点在圆外的是( )
A.(3,4)
B.(4,4)
C.(4,5)
D.(4,6)
8.如图,点ABC在同一条直线上,点D在直线AB外,过这四点中的任意3个点,能画圆的个数是( )
A.1个
B.2个
C.3个
D.4个
9.Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,则它的外心与直角顶点的距离是为( )
A.2cm
B.2.5cm
C.3cm
D.4cm
10.如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( )
A.42°
B.28°
C.21°
D.20°
二.填空题(共12小题)
11.圆上各点到圆心的距离都等于______,到圆心距离等于半径的点都在______.
12.若⊙O的半径为6cm,则⊙O中最长的弦为______厘米.
13.圆心在原点O,半径为5的⊙O,则点P(﹣3,4)在⊙O______.
14.若⊙O的半径为5cm,点A到圆心O的距离为4cm,那么点A与⊙O的位置关系是______.
15.已知圆O的直径为6,点M到圆心O的距离为4,则点M与⊙O的位置关系是______.
16.直角三角形的两直角边长分别为6和8,它的外接圆的半径是______.
17.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是______.
18.如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为______cm.
19.如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是______.
20.如图△ABC中外接圆的圆心坐标是______.
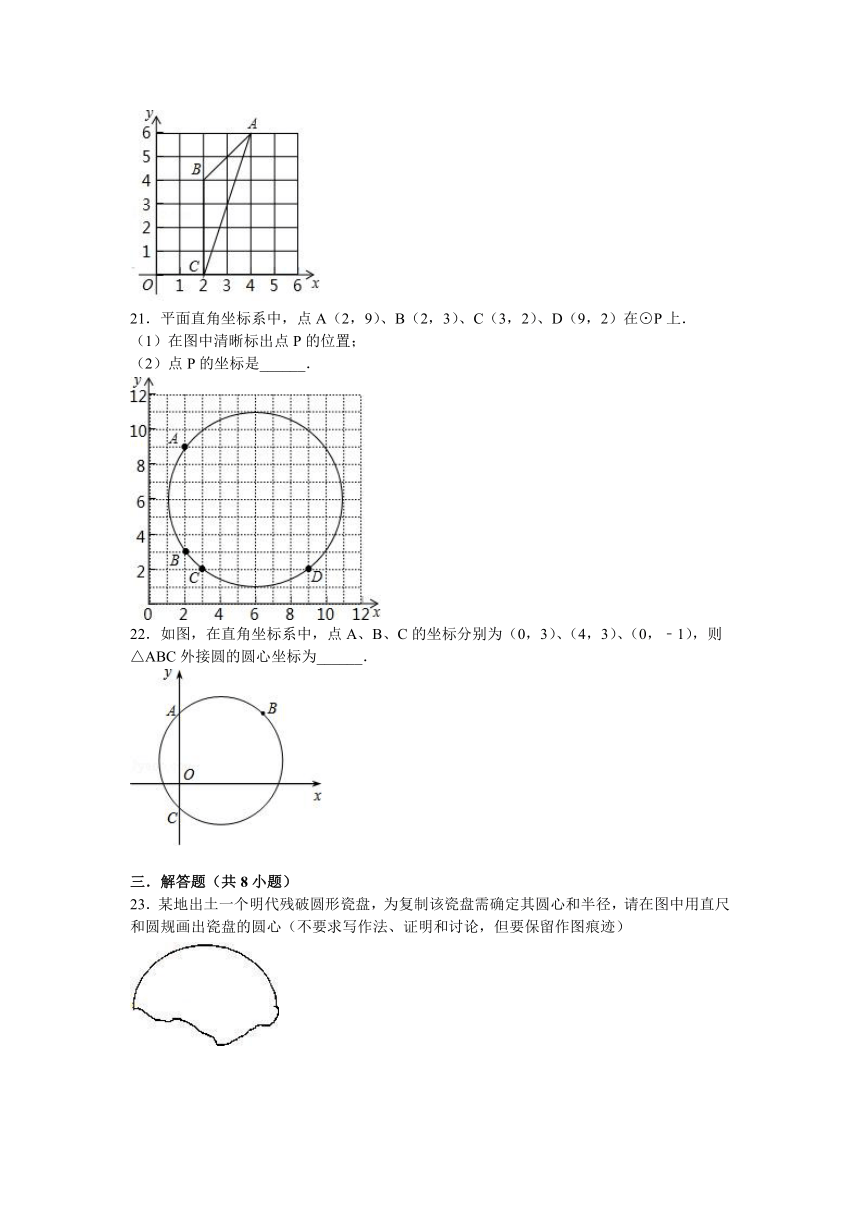
21.平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是______.
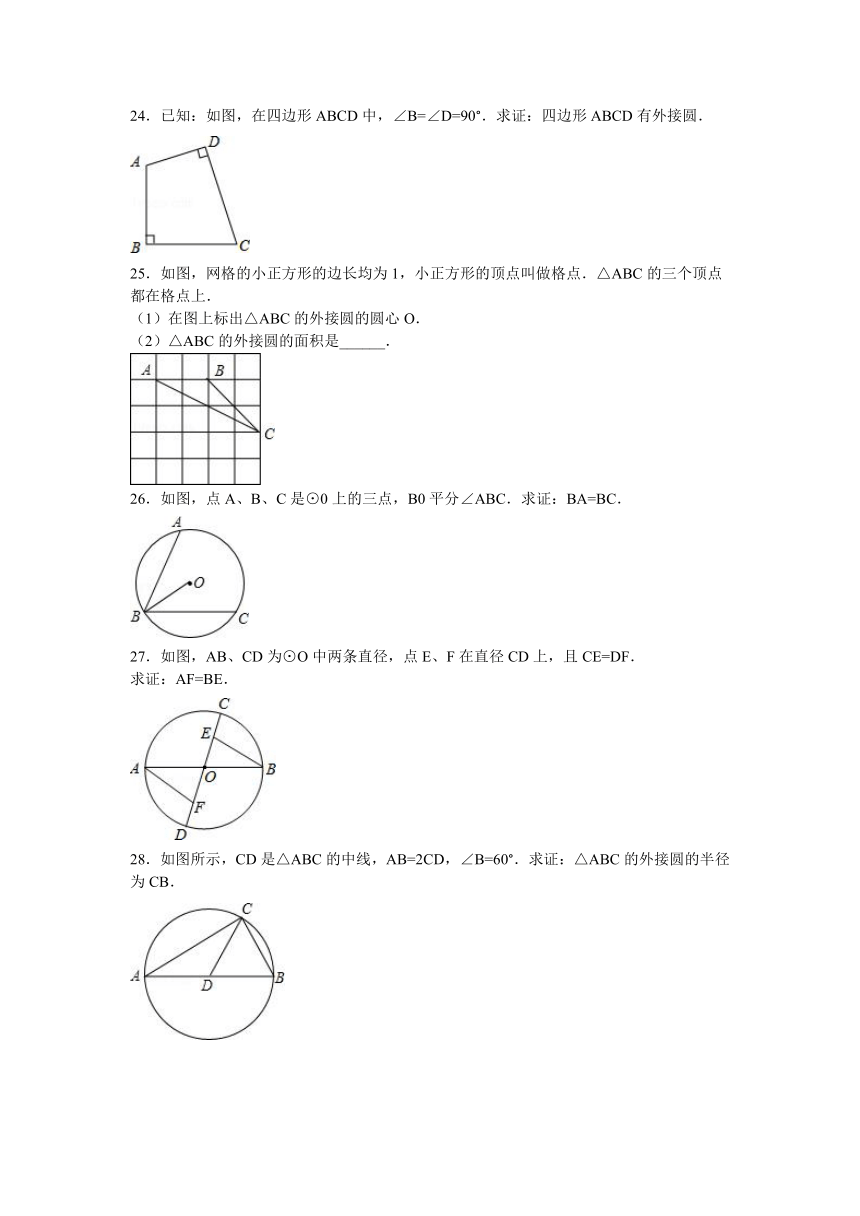
22.如图,在直角坐标系中,点A、B、C的坐标分别为(0,3)、(4,3)、(0,﹣1),则△ABC外接圆的圆心坐标为______.
三.解答题(共8小题)
23.某地出土一个明代残破圆形瓷盘,为复制该瓷盘需确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心(不要求写作法、证明和讨论,但要保留作图痕迹)
24.已知:如图,在四边形ABCD中,∠B=∠D=90°.求证:四边形ABCD有外接圆.
25.如图,网格的小正方形的边长均为1,小正方形的顶点叫做格点.△ABC的三个顶点都在格点上.
(1)在图上标出△ABC的外接圆的圆心O.
(2)△ABC的外接圆的面积是______.
26.如图,点A、B、C是⊙0上的三点,B0平分∠ABC.求证:BA=BC.
27.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
28.如图所示,CD是△ABC的中线,AB=2CD,∠B=60°.求证:△ABC的外接圆的半径为CB.
29.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
30.已知点P到圆的最大距离为11,最小距离为7,则此圆的半径为多少?(要求作图解答)
圆的概念练习题20160922
参考答案与试题解析
一.选择题(共10小题)
1.(2015春 杭州月考)下列命题正确的个数有( )
①过两点可以作无数个圆;
②经过三点一定可以作圆;
③任意一个三角形有一个外接圆,而且只有一个外接圆;
④任意一个圆有且只有一个内接三角形.
A.1个
B.2个
C.3个
D.4个
【考点】确定圆的条件;命题与定理.
【分析】分别利用确定圆的条件判断后即可确定正确的选项.
【解答】解:①过两点可以作无数个圆,正确;
②经过三点一定可以作圆,错误;
③任意一个三角形有一个外接圆,而且只有一个外接圆,正确;
④任意一个圆有且只有一个内接三角形,错误,
正确的有2个,
故选B.
2.(2013秋 仪征市校级期末)下列说法正确的是( )
A.一个点可以确定一条直线
B.两个点可以确定两条直线
C.三个点可以确定一个圆
D.不在同一直线上的三点确定一个圆
【考点】确定圆的条件;直线的性质:两点确定一条直线.
【分析】根据确定圆的条件进行判断后即可求解.
【解答】解:A、根据两点确定一条直线可知说法错误;
B、两点可以确定两条直线,故说法错误;
C、不在同一直线上的三点确定一个圆,故说法错误;
D、正确;
故选D.
3.(2015春 安岳县月考)有下列四个命题,其中正确的有( )
①圆的对称轴是直径;
②经过三个点一定可以作圆;
③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.
A.4个
B.3个
C.2个
D.1个
【考点】三角形的外接圆与外心;圆的认识;确定圆的条件.
【分析】根据圆中的有关概念、定理进行分析判断.
【解答】解:①圆的对称轴是直径所在的直线;
故此选项错误;
②当三点共线的时候,不能作圆,故此选项错误;
③三角形的外心是三角形三边的垂直平分线的交点,所以三角形的外心到三角形各顶点的距离都相等,故此选项正确;
④在同圆或等圆中,能够互相重合的弧是等弧,所以半径相等的两个半圆是等弧,故此选项正确.
故选:C.
4.(2016春 高密市期末)过圆上一点可以作出圆的最长弦的条数为( )
A.1条
B.2条
C.3条
D.无数条
【考点】圆的认识.
【分析】由于直径是圆的最长弦,经过圆心的弦是直径,两点确定一条直线,所以过圆上一点可以作出圆的最长弦的条数为一条.
【解答】解:圆的最长的弦是直径,直径经过圆心,过圆上一点和圆心可以确定一条直线,所以过圆上一点可以作出圆的最长弦的条数为一条.
故选A.
5.(2017 德州校级自主招生)⊙O的半径r=5cm,圆心到直线l的距离OM=4cm,在直线l上有一点P,且PM=3cm,则点P( )
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.可能在⊙O上或在⊙O内
【考点】点与圆的位置关系.
【分析】由条件计算出OP的长度与半径比较大小即可.
【解答】解:由题意可知△OPM为直角三角形,且PM=3,OM=4,
由勾股定理可求得OP=5=r,
故点P在⊙O上,
故选B.
6.(2016 陕西校级模拟)⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是( )
A.点P在⊙O内
B.点P的⊙O上
C.点P在⊙O外
D.点P在⊙O上或⊙O外
【考点】点与圆的位置关系;坐标与图形性质.
【分析】根据点到圆心的距离与圆的半径之间的关系:“点到圆心的距离为d,则当d=r时,点在圆上;当d>r时,点在圆外;当d<r时,点在圆内”来求解.
【解答】解:∵圆心O的坐标为(0,0),点P的坐标为(4,2),
∴OP==<5,因而点P在⊙O内.
故选A.
7.(2016春 盐都区月考)圆心在坐标原点,其半径为7的圆,则下列各点在圆外的是( )
A.(3,4)
B.(4,4)
C.(4,5)
D.(4,6)
【考点】点与圆的位置关系;坐标与图形性质.
【分析】求得各点到圆心的距离,然后利用距离与半径的大小关系即可判断.
【解答】解:A、d=5<r,所以在圆内;
B、d=4<r,所以在圆内;
C、d=<r,所以在圆内;
D、d=2>r,所以在圆外.
故选D.
8.(2014秋 宝应县校级期中)如图,点ABC在同一条直线上,点D在直线AB外,过这四点中的任意3个点,能画圆的个数是( )
A.1个
B.2个
C.3个
D.4个
【考点】确定圆的条件.
【分析】根据不在同一直线上的三点确定一个圆,进而得出答案.
【解答】解:根据题意得出:点D、A、B;点D、A、C;点D、B、C可以确定一个圆.
故过这四点中的任意3个点,能画圆的个数是3个.
故选:C.
9.(2015 会宁县一模)Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,则它的外心与直角顶点的距离是为( )
A.2cm
B.2.5cm
C.3cm
D.4cm
【考点】三角形的外接圆与外心.
【分析】先利用勾股定理计算出AB=5cm,再利用直角三角形的外心为斜边的中点得到外接圆的半径为2.5cm,于是得到它的外心与直角顶点的距离.
【解答】解:Rt△ABC中,∵∠C=90°,AC=3cm,BC=4cm,
∴AB==5cm,
∴Rt△ABC为外接圆的直径为5cm,
即△ABC的外心为AB的中点,
∴它的外心与直角顶点的距离是cm.
故选B.
10.(2016 平南县一模)如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( )
A.42°
B.28°
C.21°
D.20°
【考点】圆的认识;等腰三角形的性质.
【分析】利用半径相等得到DO=DE,则∠E=∠DOE,根据三角形外角性质得∠1=∠DOE+∠E,所以∠1=2∠E,同理得到∠AOC=∠C+∠E=3∠E,然后利用∠E=∠AOC进行计算即可.
【解答】解:连结OD,如图,
∵OB=DE,OB=OD,
∴DO=DE,
∴∠E=∠DOE,
∵∠1=∠DOE+∠E,
∴∠1=2∠E,
而OC=OD,
∴∠C=∠1,
∴∠C=2∠E,
∴∠AOC=∠C+∠E=3∠E,
∴∠E=∠AOC=×84°=28°.
故选B.
二.填空题(共12小题)
11.(2013秋 仪征市校级期末)圆上各点到圆心的距离都等于 圆的半径 ,到圆心距离等于半径的点都在 圆上 .
【考点】圆的认识.
【分析】根据圆的定义求解.
【解答】解:圆上各点到圆心的距离都等于圆的半径,到圆心的距离等于半径的点都在圆上.
故答案为圆的半径,圆上.
12.(2015春 高密市期末)若⊙O的半径为6cm,则⊙O中最长的弦为 12 厘米.
【考点】圆的认识.
【分析】根据直径为圆的最长弦求解.
【解答】解:∵⊙O的半径为6cm,
∴⊙O的直径为12cm,
即圆中最长的弦长为12cm.
故答案为12.
13.(2016 德州校级自主招生)圆心在原点O,半径为5的⊙O,则点P(﹣3,4)在⊙O 上 .
【考点】点与圆的位置关系;坐标与图形性质.
【分析】先由勾股定理求得点P到圆心O的距离,再根据点P与圆心的距离与半径的大小关系,来判断出点P与⊙O的位置关系.
【解答】解:∵点P的坐标为(﹣3,4),
∴由勾股定理得,点P到圆心O的距离==5,
∴点P在⊙O上.
故答案为上.
14.(2015秋 江都区校级期末)若⊙O的半径为5cm,点A到圆心O的距离为4cm,那么点A与⊙O的位置关系是 点A在圆内 .
【考点】点与圆的位置关系.
【分析】要确定点与圆的位置关系,主要确定点与圆心的距离与半径的大小关系;利用d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内判断出即可.
【解答】解:∵⊙O的半径为5cm,点A到圆心O的距离为4cm,
∴d<r,
∴点A与⊙O的位置关系是:点A在圆内,
故答案为:点A在圆内.
15.(2015秋 宝应县校级月考)已知圆O的直径为6,点M到圆心O的距离为4,则点M与⊙O的位置关系是 在圆外 .
【考点】点与圆的位置关系.
【分析】要确定点与圆的位置关系,主要确定点与圆心的距离与半径的大小关系;若设点到圆心的距离为d,圆的半径为r,则d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
【解答】解:∵⊙O的直径为6,
∴⊙O的半径为3,
∵点M到圆心O的距离为4,
∴4>3,
∴点M在⊙O外.
故答案为:在圆外.
16.(2015秋 姜堰市期中)直角三角形的两直角边长分别为6和8,它的外接圆的半径是 5 .
【考点】三角形的外接圆与外心.
【分析】首先根据勾股定理,得斜边是10,再根据其外接圆的半径是斜边的一半,得出其外接圆的半径.
【解答】解:∵直角边长分别为6和8,
∴斜边是10,
∴这个直角三角形的外接圆的半径为5.
故答案为:5.
17.(2015秋 邗江区校级月考)如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是 10 .
【考点】圆的认识;勾股定理.
【分析】先连接OC,在Rt△ODC中,根据勾股定理得出OC的长,即可求出AB的长.
【解答】解:连接OC,
∵CD=4,OD=3,
在Rt△ODC中,
∴OC===5,
∴AB=2OC=10,
故答案为:10.
18.(2014秋 天河区校级期中)如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为 4 cm.
【考点】圆的认识;等边三角形的判定与性质.
【分析】利用半径相等可判断△OAB为等边三角形,然后根据等边三角形的性质易得AB=4cm.
【解答】解:∵OA=OB,
而∠AOB=60°,
∴△OAB为等边三角形,
∴AB=OA=4cm.
故答案为4.
19.(2015 盐城)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 3<r<5 .
【考点】点与圆的位置关系.
【分析】要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
【解答】解:在直角△ABD中,CD=AB=4,AD=3,
则BD==5.
由图可知3<r<5.
故答案为:3<r<5.
20.(2011秋 清河区校级期末)如图△ABC中外接圆的圆心坐标是 (6,2) .
【考点】确定圆的条件;坐标与图形性质.
【分析】本题可借助网格在网格中根据三角形三边的位置作出它们的垂直平分线,垂直平分线相交于一点,该点就是圆心,根据网格中的单位长度即可求解.
【解答】解:分别做三角形的三边的垂直平分线,可知相交于点(6,2),
即△ABC中外接圆的圆心坐标是(6,2).
故答案为:(6,2).
21.(2005 江西)平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是 (6,6) .
【考点】确定圆的条件;坐标与图形性质.
【分析】点P的坐标是弦AB,CD的垂直平分线的交点.
【解答】解:弦AB的垂直平分线是y=6,弦CD的垂直平分线是x=6,因而交点P的坐标是(6,6).
22.(2015 高淳县二模)如图,在直角坐标系中,点A、B、C的坐标分别为(0,3)、(4,3)、(0,﹣1),则△ABC外接圆的圆心坐标为 (2,1) .
【考点】三角形的外接圆与外心;坐标与图形性质.
【分析】根据垂径定理的推论“弦的垂直平分线必过圆心”,作两条弦的垂直平分线,交点即为圆心.
【解答】解:根据垂径定理的推论,则
作弦AB、AC的垂直平分线,交点O1即为圆心,
∵点A、B、C的坐标分别为(0,3)、(4,3)、(0,﹣1),
∴O1的坐标是(2,1).
故答案为:(2,1).
三.解答题(共8小题)
23.(2009秋 河西区期末)某地出土一个明代残破圆形瓷盘,为复制该瓷盘需确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心(不要求写作法、证明和讨论,但要保留作图痕迹)
【考点】确定圆的条件.
【分析】根据垂径定理,在残破的圆形瓷盘上任取两个弦,分别作弦的垂直平分线即可.
【解答】解:在圆上取两个弦,根据垂径定理,
垂直平分弦的直线一定过圆心,
所以作出两弦的垂直平分线即可.
24.(2015秋 阜宁县期中)已知:如图,在四边形ABCD中,∠B=∠D=90°.求证:四边形ABCD有外接圆.
【考点】三角形的外接圆与外心.
【分析】根据直角三角形的斜边是其外接圆的直径,可得A,B,C,D都在以AC为直径的圆上.
【解答】证明:∵∠ABC=90°,
∴AC是△ABC的外接圆⊙O的直径,
而∠ADC=90°,
∴点D在⊙O上,
即四边形ABCD有外接圆.
25.(2013秋 如皋市期中)如图,网格的小正方形的边长均为1,小正方形的顶点叫做格点.△ABC的三个顶点都在格点上.
(1)在图上标出△ABC的外接圆的圆心O.
(2)△ABC的外接圆的面积是 10π .
【考点】三角形的外接圆与外心.
【分析】(1)根据三角形外心的确定方法得出O点位置即可;
(2)利用勾股定理得出AO的长,再利用圆的面积公式得出即可.
【解答】
解:(1)在图上标出
的外接圆的圆心O;
(2)∵AO==,
∴外接圆的面积是10π.
故答案为:10π.
26.(2012 道外区二模)如图,点A、B、C是⊙0上的三点,B0平分∠ABC.求证:BA=BC.
【考点】圆的认识;全等三角形的判定与性质.
【分析】连OA、OC,利用半径都相等得到OA=OB,OB=OC,根据等腰三角形的性质有∠ABO=∠BAO,∠CBO=∠BCO,而B0平分∠ABC,则∠ABO=∠CBO,根据三角形全等的判定得到△OAB≌△OCB,即可得到结论.
【解答】证明:连OA、OC,如图,
∵OA=OB,OB=OC,
∴∠ABO=∠BAO,∠CBO=∠BCO,
∵B0平分∠ABC,
∴∠ABO=∠CBO,
∴∠BAO=∠BCO,
∴△OAB≌△OCB,
∴AB=BC.
27.(2012 淮安模拟)如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
【考点】圆的认识;全等三角形的判定与性质.
【分析】根据AB、CD为⊙O中两条直径,得出OA=OB,OC=OD,再根据CE=DF,得出OE=OF,从而证出△AOF和△BOE全等,即可得出答案.
【解答】解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
28.如图所示,CD是△ABC的中线,AB=2CD,∠B=60°.求证:△ABC的外接圆的半径为CB.
【考点】三角形的外接圆与外心.
【分析】利用三角形中线的性质以及等边三角形的判定方法得出△BDC是等边三角形,进而得出∠ACB=90°,求出BC=AB,即可得出答案.
【解答】证明:∵CD是△ABC的中线,AB=2CD,
∴AD=BD=CD,
∵∠B=60°,
∴△CDB是等边三角形,
∴∠BDC=∠DCB=60°,
∴∠A=∠ACD=30°,
∴∠ACB=90°,
∴AB是△ABC的外接圆的直径,
∵∠A=30°,∠ACB=90°,
∴BC=AB,
∴△ABC的外接圆的半径为CB.
29.(2016春 海口校级月考)如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
【考点】圆的认识;等腰三角形的性质.
【分析】连接OD,如图,由AB=2DE,AB=2OD得到OD=DE,根据等腰三角形的性质得∠DOE=∠E=20°,再利用三角形外角性质得到∠CDO=40°,加上∠C=∠ODC=40°,然后再利用三角形外角性质即可计算出∠AOC.
【解答】解:连接OD,如图,
∵AB=2DE,
而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°,
而OC=OD,
∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
30.(2013秋 榆阳区校级期末)已知点P到圆的最大距离为11,最小距离为7,则此圆的半径为多少?(要求作图解答)
【考点】点与圆的位置关系.
【分析】点P应分为位于圆的内部位于外部两种情况讨论.当点P在圆内时,点到圆的最大距离与最小距离的和是直径;当点P在圆外时,点到圆的最大距离与最小距离的差是直径,由此得解.
【解答】解:如图,分为两种情况:
①当点P在圆内时,最近点的距离为7,最大距离为11,则直径是18,因而半径是9;
②当点P在圆外时,最近点的距离为7,最大距离为11,则直径是4,因而半径是2.
故此圆的半径为2或9.
一.选择题(共10小题)
1.下列命题正确的个数有( )
①过两点可以作无数个圆;
②经过三点一定可以作圆;
③任意一个三角形有一个外接圆,而且只有一个外接圆;
④任意一个圆有且只有一个内接三角形.
A.1个
B.2个
C.3个
D.4个
2.下列说法正确的是( )
A.一个点可以确定一条直线
B.两个点可以确定两条直线
C.三个点可以确定一个圆
D.不在同一直线上的三点确定一个圆
3.有下列四个命题,其中正确的有( )
①圆的对称轴是直径;
②经过三个点一定可以作圆;
③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.
A.4个
B.3个
C.2个
D.1个
4.过圆上一点可以作出圆的最长弦的条数为( )
A.1条
B.2条
C.3条
D.无数条
5.⊙O的半径r=5cm,圆心到直线l的距离OM=4cm,在直线l上有一点P,且PM=3cm,则点P( )
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.可能在⊙O上或在⊙O内
6.⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是( )
A.点P在⊙O内
B.点P的⊙O上
C.点P在⊙O外
D.点P在⊙O上或⊙O外
7.圆心在坐标原点,其半径为7的圆,则下列各点在圆外的是( )
A.(3,4)
B.(4,4)
C.(4,5)
D.(4,6)
8.如图,点ABC在同一条直线上,点D在直线AB外,过这四点中的任意3个点,能画圆的个数是( )
A.1个
B.2个
C.3个
D.4个
9.Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,则它的外心与直角顶点的距离是为( )
A.2cm
B.2.5cm
C.3cm
D.4cm
10.如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( )
A.42°
B.28°
C.21°
D.20°
二.填空题(共12小题)
11.圆上各点到圆心的距离都等于______,到圆心距离等于半径的点都在______.
12.若⊙O的半径为6cm,则⊙O中最长的弦为______厘米.
13.圆心在原点O,半径为5的⊙O,则点P(﹣3,4)在⊙O______.
14.若⊙O的半径为5cm,点A到圆心O的距离为4cm,那么点A与⊙O的位置关系是______.
15.已知圆O的直径为6,点M到圆心O的距离为4,则点M与⊙O的位置关系是______.
16.直角三角形的两直角边长分别为6和8,它的外接圆的半径是______.
17.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是______.
18.如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为______cm.
19.如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是______.
20.如图△ABC中外接圆的圆心坐标是______.
21.平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是______.
22.如图,在直角坐标系中,点A、B、C的坐标分别为(0,3)、(4,3)、(0,﹣1),则△ABC外接圆的圆心坐标为______.
三.解答题(共8小题)
23.某地出土一个明代残破圆形瓷盘,为复制该瓷盘需确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心(不要求写作法、证明和讨论,但要保留作图痕迹)
24.已知:如图,在四边形ABCD中,∠B=∠D=90°.求证:四边形ABCD有外接圆.
25.如图,网格的小正方形的边长均为1,小正方形的顶点叫做格点.△ABC的三个顶点都在格点上.
(1)在图上标出△ABC的外接圆的圆心O.
(2)△ABC的外接圆的面积是______.
26.如图,点A、B、C是⊙0上的三点,B0平分∠ABC.求证:BA=BC.
27.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
28.如图所示,CD是△ABC的中线,AB=2CD,∠B=60°.求证:△ABC的外接圆的半径为CB.
29.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
30.已知点P到圆的最大距离为11,最小距离为7,则此圆的半径为多少?(要求作图解答)
圆的概念练习题20160922
参考答案与试题解析
一.选择题(共10小题)
1.(2015春 杭州月考)下列命题正确的个数有( )
①过两点可以作无数个圆;
②经过三点一定可以作圆;
③任意一个三角形有一个外接圆,而且只有一个外接圆;
④任意一个圆有且只有一个内接三角形.
A.1个
B.2个
C.3个
D.4个
【考点】确定圆的条件;命题与定理.
【分析】分别利用确定圆的条件判断后即可确定正确的选项.
【解答】解:①过两点可以作无数个圆,正确;
②经过三点一定可以作圆,错误;
③任意一个三角形有一个外接圆,而且只有一个外接圆,正确;
④任意一个圆有且只有一个内接三角形,错误,
正确的有2个,
故选B.
2.(2013秋 仪征市校级期末)下列说法正确的是( )
A.一个点可以确定一条直线
B.两个点可以确定两条直线
C.三个点可以确定一个圆
D.不在同一直线上的三点确定一个圆
【考点】确定圆的条件;直线的性质:两点确定一条直线.
【分析】根据确定圆的条件进行判断后即可求解.
【解答】解:A、根据两点确定一条直线可知说法错误;
B、两点可以确定两条直线,故说法错误;
C、不在同一直线上的三点确定一个圆,故说法错误;
D、正确;
故选D.
3.(2015春 安岳县月考)有下列四个命题,其中正确的有( )
①圆的对称轴是直径;
②经过三个点一定可以作圆;
③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.
A.4个
B.3个
C.2个
D.1个
【考点】三角形的外接圆与外心;圆的认识;确定圆的条件.
【分析】根据圆中的有关概念、定理进行分析判断.
【解答】解:①圆的对称轴是直径所在的直线;
故此选项错误;
②当三点共线的时候,不能作圆,故此选项错误;
③三角形的外心是三角形三边的垂直平分线的交点,所以三角形的外心到三角形各顶点的距离都相等,故此选项正确;
④在同圆或等圆中,能够互相重合的弧是等弧,所以半径相等的两个半圆是等弧,故此选项正确.
故选:C.
4.(2016春 高密市期末)过圆上一点可以作出圆的最长弦的条数为( )
A.1条
B.2条
C.3条
D.无数条
【考点】圆的认识.
【分析】由于直径是圆的最长弦,经过圆心的弦是直径,两点确定一条直线,所以过圆上一点可以作出圆的最长弦的条数为一条.
【解答】解:圆的最长的弦是直径,直径经过圆心,过圆上一点和圆心可以确定一条直线,所以过圆上一点可以作出圆的最长弦的条数为一条.
故选A.
5.(2017 德州校级自主招生)⊙O的半径r=5cm,圆心到直线l的距离OM=4cm,在直线l上有一点P,且PM=3cm,则点P( )
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.可能在⊙O上或在⊙O内
【考点】点与圆的位置关系.
【分析】由条件计算出OP的长度与半径比较大小即可.
【解答】解:由题意可知△OPM为直角三角形,且PM=3,OM=4,
由勾股定理可求得OP=5=r,
故点P在⊙O上,
故选B.
6.(2016 陕西校级模拟)⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是( )
A.点P在⊙O内
B.点P的⊙O上
C.点P在⊙O外
D.点P在⊙O上或⊙O外
【考点】点与圆的位置关系;坐标与图形性质.
【分析】根据点到圆心的距离与圆的半径之间的关系:“点到圆心的距离为d,则当d=r时,点在圆上;当d>r时,点在圆外;当d<r时,点在圆内”来求解.
【解答】解:∵圆心O的坐标为(0,0),点P的坐标为(4,2),
∴OP==<5,因而点P在⊙O内.
故选A.
7.(2016春 盐都区月考)圆心在坐标原点,其半径为7的圆,则下列各点在圆外的是( )
A.(3,4)
B.(4,4)
C.(4,5)
D.(4,6)
【考点】点与圆的位置关系;坐标与图形性质.
【分析】求得各点到圆心的距离,然后利用距离与半径的大小关系即可判断.
【解答】解:A、d=5<r,所以在圆内;
B、d=4<r,所以在圆内;
C、d=<r,所以在圆内;
D、d=2>r,所以在圆外.
故选D.
8.(2014秋 宝应县校级期中)如图,点ABC在同一条直线上,点D在直线AB外,过这四点中的任意3个点,能画圆的个数是( )
A.1个
B.2个
C.3个
D.4个
【考点】确定圆的条件.
【分析】根据不在同一直线上的三点确定一个圆,进而得出答案.
【解答】解:根据题意得出:点D、A、B;点D、A、C;点D、B、C可以确定一个圆.
故过这四点中的任意3个点,能画圆的个数是3个.
故选:C.
9.(2015 会宁县一模)Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,则它的外心与直角顶点的距离是为( )
A.2cm
B.2.5cm
C.3cm
D.4cm
【考点】三角形的外接圆与外心.
【分析】先利用勾股定理计算出AB=5cm,再利用直角三角形的外心为斜边的中点得到外接圆的半径为2.5cm,于是得到它的外心与直角顶点的距离.
【解答】解:Rt△ABC中,∵∠C=90°,AC=3cm,BC=4cm,
∴AB==5cm,
∴Rt△ABC为外接圆的直径为5cm,
即△ABC的外心为AB的中点,
∴它的外心与直角顶点的距离是cm.
故选B.
10.(2016 平南县一模)如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( )
A.42°
B.28°
C.21°
D.20°
【考点】圆的认识;等腰三角形的性质.
【分析】利用半径相等得到DO=DE,则∠E=∠DOE,根据三角形外角性质得∠1=∠DOE+∠E,所以∠1=2∠E,同理得到∠AOC=∠C+∠E=3∠E,然后利用∠E=∠AOC进行计算即可.
【解答】解:连结OD,如图,
∵OB=DE,OB=OD,
∴DO=DE,
∴∠E=∠DOE,
∵∠1=∠DOE+∠E,
∴∠1=2∠E,
而OC=OD,
∴∠C=∠1,
∴∠C=2∠E,
∴∠AOC=∠C+∠E=3∠E,
∴∠E=∠AOC=×84°=28°.
故选B.
二.填空题(共12小题)
11.(2013秋 仪征市校级期末)圆上各点到圆心的距离都等于 圆的半径 ,到圆心距离等于半径的点都在 圆上 .
【考点】圆的认识.
【分析】根据圆的定义求解.
【解答】解:圆上各点到圆心的距离都等于圆的半径,到圆心的距离等于半径的点都在圆上.
故答案为圆的半径,圆上.
12.(2015春 高密市期末)若⊙O的半径为6cm,则⊙O中最长的弦为 12 厘米.
【考点】圆的认识.
【分析】根据直径为圆的最长弦求解.
【解答】解:∵⊙O的半径为6cm,
∴⊙O的直径为12cm,
即圆中最长的弦长为12cm.
故答案为12.
13.(2016 德州校级自主招生)圆心在原点O,半径为5的⊙O,则点P(﹣3,4)在⊙O 上 .
【考点】点与圆的位置关系;坐标与图形性质.
【分析】先由勾股定理求得点P到圆心O的距离,再根据点P与圆心的距离与半径的大小关系,来判断出点P与⊙O的位置关系.
【解答】解:∵点P的坐标为(﹣3,4),
∴由勾股定理得,点P到圆心O的距离==5,
∴点P在⊙O上.
故答案为上.
14.(2015秋 江都区校级期末)若⊙O的半径为5cm,点A到圆心O的距离为4cm,那么点A与⊙O的位置关系是 点A在圆内 .
【考点】点与圆的位置关系.
【分析】要确定点与圆的位置关系,主要确定点与圆心的距离与半径的大小关系;利用d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内判断出即可.
【解答】解:∵⊙O的半径为5cm,点A到圆心O的距离为4cm,
∴d<r,
∴点A与⊙O的位置关系是:点A在圆内,
故答案为:点A在圆内.
15.(2015秋 宝应县校级月考)已知圆O的直径为6,点M到圆心O的距离为4,则点M与⊙O的位置关系是 在圆外 .
【考点】点与圆的位置关系.
【分析】要确定点与圆的位置关系,主要确定点与圆心的距离与半径的大小关系;若设点到圆心的距离为d,圆的半径为r,则d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
【解答】解:∵⊙O的直径为6,
∴⊙O的半径为3,
∵点M到圆心O的距离为4,
∴4>3,
∴点M在⊙O外.
故答案为:在圆外.
16.(2015秋 姜堰市期中)直角三角形的两直角边长分别为6和8,它的外接圆的半径是 5 .
【考点】三角形的外接圆与外心.
【分析】首先根据勾股定理,得斜边是10,再根据其外接圆的半径是斜边的一半,得出其外接圆的半径.
【解答】解:∵直角边长分别为6和8,
∴斜边是10,
∴这个直角三角形的外接圆的半径为5.
故答案为:5.
17.(2015秋 邗江区校级月考)如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是 10 .
【考点】圆的认识;勾股定理.
【分析】先连接OC,在Rt△ODC中,根据勾股定理得出OC的长,即可求出AB的长.
【解答】解:连接OC,
∵CD=4,OD=3,
在Rt△ODC中,
∴OC===5,
∴AB=2OC=10,
故答案为:10.
18.(2014秋 天河区校级期中)如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为 4 cm.
【考点】圆的认识;等边三角形的判定与性质.
【分析】利用半径相等可判断△OAB为等边三角形,然后根据等边三角形的性质易得AB=4cm.
【解答】解:∵OA=OB,
而∠AOB=60°,
∴△OAB为等边三角形,
∴AB=OA=4cm.
故答案为4.
19.(2015 盐城)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 3<r<5 .
【考点】点与圆的位置关系.
【分析】要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
【解答】解:在直角△ABD中,CD=AB=4,AD=3,
则BD==5.
由图可知3<r<5.
故答案为:3<r<5.
20.(2011秋 清河区校级期末)如图△ABC中外接圆的圆心坐标是 (6,2) .
【考点】确定圆的条件;坐标与图形性质.
【分析】本题可借助网格在网格中根据三角形三边的位置作出它们的垂直平分线,垂直平分线相交于一点,该点就是圆心,根据网格中的单位长度即可求解.
【解答】解:分别做三角形的三边的垂直平分线,可知相交于点(6,2),
即△ABC中外接圆的圆心坐标是(6,2).
故答案为:(6,2).
21.(2005 江西)平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是 (6,6) .
【考点】确定圆的条件;坐标与图形性质.
【分析】点P的坐标是弦AB,CD的垂直平分线的交点.
【解答】解:弦AB的垂直平分线是y=6,弦CD的垂直平分线是x=6,因而交点P的坐标是(6,6).
22.(2015 高淳县二模)如图,在直角坐标系中,点A、B、C的坐标分别为(0,3)、(4,3)、(0,﹣1),则△ABC外接圆的圆心坐标为 (2,1) .
【考点】三角形的外接圆与外心;坐标与图形性质.
【分析】根据垂径定理的推论“弦的垂直平分线必过圆心”,作两条弦的垂直平分线,交点即为圆心.
【解答】解:根据垂径定理的推论,则
作弦AB、AC的垂直平分线,交点O1即为圆心,
∵点A、B、C的坐标分别为(0,3)、(4,3)、(0,﹣1),
∴O1的坐标是(2,1).
故答案为:(2,1).
三.解答题(共8小题)
23.(2009秋 河西区期末)某地出土一个明代残破圆形瓷盘,为复制该瓷盘需确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心(不要求写作法、证明和讨论,但要保留作图痕迹)
【考点】确定圆的条件.
【分析】根据垂径定理,在残破的圆形瓷盘上任取两个弦,分别作弦的垂直平分线即可.
【解答】解:在圆上取两个弦,根据垂径定理,
垂直平分弦的直线一定过圆心,
所以作出两弦的垂直平分线即可.
24.(2015秋 阜宁县期中)已知:如图,在四边形ABCD中,∠B=∠D=90°.求证:四边形ABCD有外接圆.
【考点】三角形的外接圆与外心.
【分析】根据直角三角形的斜边是其外接圆的直径,可得A,B,C,D都在以AC为直径的圆上.
【解答】证明:∵∠ABC=90°,
∴AC是△ABC的外接圆⊙O的直径,
而∠ADC=90°,
∴点D在⊙O上,
即四边形ABCD有外接圆.
25.(2013秋 如皋市期中)如图,网格的小正方形的边长均为1,小正方形的顶点叫做格点.△ABC的三个顶点都在格点上.
(1)在图上标出△ABC的外接圆的圆心O.
(2)△ABC的外接圆的面积是 10π .
【考点】三角形的外接圆与外心.
【分析】(1)根据三角形外心的确定方法得出O点位置即可;
(2)利用勾股定理得出AO的长,再利用圆的面积公式得出即可.
【解答】
解:(1)在图上标出
的外接圆的圆心O;
(2)∵AO==,
∴外接圆的面积是10π.
故答案为:10π.
26.(2012 道外区二模)如图,点A、B、C是⊙0上的三点,B0平分∠ABC.求证:BA=BC.
【考点】圆的认识;全等三角形的判定与性质.
【分析】连OA、OC,利用半径都相等得到OA=OB,OB=OC,根据等腰三角形的性质有∠ABO=∠BAO,∠CBO=∠BCO,而B0平分∠ABC,则∠ABO=∠CBO,根据三角形全等的判定得到△OAB≌△OCB,即可得到结论.
【解答】证明:连OA、OC,如图,
∵OA=OB,OB=OC,
∴∠ABO=∠BAO,∠CBO=∠BCO,
∵B0平分∠ABC,
∴∠ABO=∠CBO,
∴∠BAO=∠BCO,
∴△OAB≌△OCB,
∴AB=BC.
27.(2012 淮安模拟)如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
【考点】圆的认识;全等三角形的判定与性质.
【分析】根据AB、CD为⊙O中两条直径,得出OA=OB,OC=OD,再根据CE=DF,得出OE=OF,从而证出△AOF和△BOE全等,即可得出答案.
【解答】解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
28.如图所示,CD是△ABC的中线,AB=2CD,∠B=60°.求证:△ABC的外接圆的半径为CB.
【考点】三角形的外接圆与外心.
【分析】利用三角形中线的性质以及等边三角形的判定方法得出△BDC是等边三角形,进而得出∠ACB=90°,求出BC=AB,即可得出答案.
【解答】证明:∵CD是△ABC的中线,AB=2CD,
∴AD=BD=CD,
∵∠B=60°,
∴△CDB是等边三角形,
∴∠BDC=∠DCB=60°,
∴∠A=∠ACD=30°,
∴∠ACB=90°,
∴AB是△ABC的外接圆的直径,
∵∠A=30°,∠ACB=90°,
∴BC=AB,
∴△ABC的外接圆的半径为CB.
29.(2016春 海口校级月考)如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
【考点】圆的认识;等腰三角形的性质.
【分析】连接OD,如图,由AB=2DE,AB=2OD得到OD=DE,根据等腰三角形的性质得∠DOE=∠E=20°,再利用三角形外角性质得到∠CDO=40°,加上∠C=∠ODC=40°,然后再利用三角形外角性质即可计算出∠AOC.
【解答】解:连接OD,如图,
∵AB=2DE,
而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°,
而OC=OD,
∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
30.(2013秋 榆阳区校级期末)已知点P到圆的最大距离为11,最小距离为7,则此圆的半径为多少?(要求作图解答)
【考点】点与圆的位置关系.
【分析】点P应分为位于圆的内部位于外部两种情况讨论.当点P在圆内时,点到圆的最大距离与最小距离的和是直径;当点P在圆外时,点到圆的最大距离与最小距离的差是直径,由此得解.
【解答】解:如图,分为两种情况:
①当点P在圆内时,最近点的距离为7,最大距离为11,则直径是18,因而半径是9;
②当点P在圆外时,最近点的距离为7,最大距离为11,则直径是4,因而半径是2.
故此圆的半径为2或9.
同课章节目录
