1.4二次函数的实际应用学案(无答案）

天天享学初三数学一对一讲义
主讲人：徐泓标（PEC教师）
授课时间：
学生姓名：
课后完成质量：
【解决最优问题】
对于二次函数
二次函数的性质1——最值
a＞0
a＜0
二次函数的性质2——单调性
a＞0
a＜0
例题
某宾馆有50个房间供游客住宿，当每个房间的价格为每天180元时，房间会全部住满。当每个房间每天的房价每增加10元时，就会有一个房间空闲。宾馆需对游客居住的每个房间每天支出20元的各种费用。根据规定，每个房间每天的房价不得高于340元。设每个房间的房价增加x元（x为10的正整数倍）。
（1）设一天订住的房间数为y，直接写出y与x的函数关系式及自变量的取值范围；
（2）设宾馆一天的利润为w元，求w与x的函数关系式；
（3）一天订住多少个房间时，宾馆的利润最大？最大为多少？
【解决几个球】
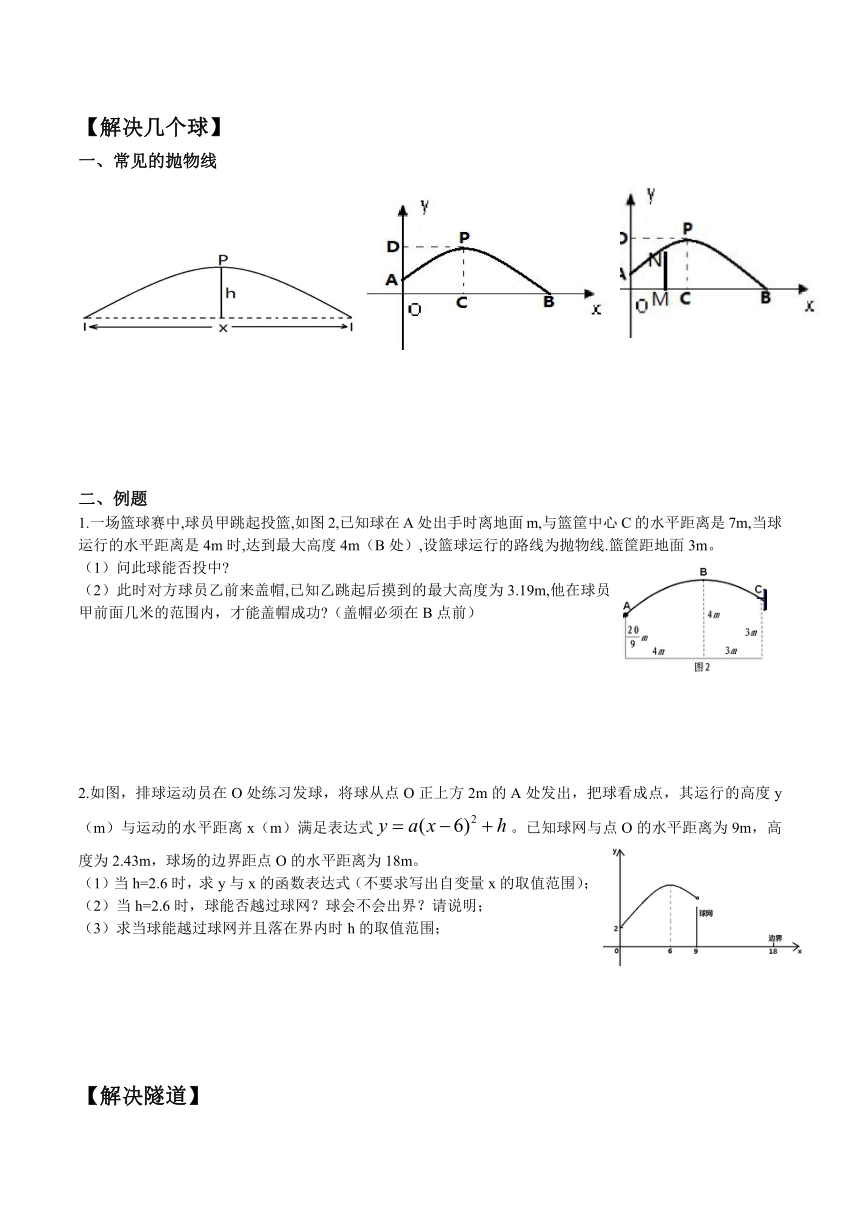
常见的抛物线
二、例题
1.一场篮球赛中,球员甲跳起投篮,如图2,已知球在A处出手时离地面m,与篮筐中心C的水平距离是7m,当球运行的水平距离是4m时,达到最大高度4m（B处）,设篮球运行的路线为抛物线.篮筐距地面3m。
（1）问此球能否投中
（2）此时对方球员乙前来盖帽,已知乙跳起后摸到的最大高度为3.19m,他在球员甲前面几米的范围内，才能盖帽成功 （盖帽必须在B点前）
2.如图，排球运动员在O处练习发球，将球从点O正上方2m的A处发出，把球看成点，其运行的高度y（m）与运动的水平距离x（m）满足表达式。已知球网与点O的水平距离为9m，高度为2.43m，球场的边界距点O的水平距离为18m。
（1）当h=2.6时，求y与x的函数表达式（不要求写出自变量x的取值范围）；
（2）当h=2.6时，球能否越过球网？球会不会出界？请说明；
（3）求当球能越过球网并且落在界内时h的取值范围；
【解决隧道】
一、过隧道：桥洞或隧道的通过问题指的是讨论矩形物体（简单化后的车、船等）能否通过二次函数曲线的隧道或桥洞，如图为常见模型（以隧道为例），该模型的主要特点：
①抛物线模型和计算二次函数表达式与桥洞模型类似；
②抛物线内的矩形为货车简化图，为尽可能通过隧道，一般货车行驶在隧道中央，其高度为h；
③Q在抛物线上，PQ表示当货车左侧在P点时，隧道在此处的高度。且PQ=PR-QR。
例题
如图，小河上有一拱桥，拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、DE、DB组成，已知河底DE是水平的，DE=16m，AE=8m，抛物线的顶点C到DE的距离是11m，以DE所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系。
求该抛物线的解析式；
现有一艘货船需要载着每块长6m，宽4m，的木材通过此桥洞。已知货船吃重后船上沿距离河底DE恒定为4m，求从船上沿往上放置木材，最多一次性能放置多高？
【针对练习题】
1.某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元，为了扩大销售，增加盈利，尽快减少库存，商场判定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件。
若商场平均每天要盈利1200元，每件衬衫应降价多少元？
每件衬衫降低多少元时，商场平均每天盈利最多？
2.某公司新开发一种电子产品，现准备从国内和国外两种销售方案中选择一种进行销售。若只在国内销售，销售价格y（元/件）与月销量x（件）之间的函数关系式为，成本为20元/件，无论销售多少，每月还需支出广告费62500元，设月利润为w内（元）（利润=销售额—成本—广告费）。若只在国外销售，销售价格为150元/件，受各种不确定因素影响，成本为a元/件（a为常数，）当月销量为x（件）时，每月还需缴纳元的附加费，设月利润为w外（元）（利润=销售额—成本—附加费）。
（1）若在国内销售，当月销售量为1000件，该产品的销售价格和月利润分别是多少元？当月销售量为多少件时，在国内销售的月利润最大？最大利润是多少？
（2）若在国外销售月利润的最大值与在国内销售月利润的最大值相同，求a的值；
（3）如果某月要将5000件产品全部销售完，请你通过分析帮助公司决策，选择在国内销售还是在国外销售才能使所获月利润较大？
3.如图，在体育测试时，一位初三同学掷铅球，已知铅球所经过的路线是二次函数的一部分，如果这个同学出手点A的坐标为（0，2），铅球路线最高处B的坐标为（6，5）
求这条二次函数的解析式；
（2）该生能把铅球掷多远？（精确到0.01米，≈3.873）
4.某校运动会上，某运动员掷铅球时，他所掷的铅球的高
与水平的距离
，则该运动员的成绩是(
)
A.
6m
B.
10m
C.
8m
D.
12m
5.小敏在今年的校运动会跳远比赛中跳出了满意一跳，函数h=3．5
t－4．9
t2(t的单位s；h中的单位：m）可以描述他跳跃时
重心高度的变化．如图1－2－41，则他起跳后到重心最高时所用的时间是（
）
A．0．71s
B．0.70s
C．0.63s
D．0．36s
6.有一座抛物线形拱桥，在正常水位时水面AB的宽为20m，如果水位上升3m时，水面CD的宽为10m。
（1）建立如图所示直角坐标系，求此抛物线的解析式；
（2）现有一辆载有救援物质的货车从甲地出发需经过此桥开往乙地，已知甲地距此桥
280km（桥长忽略不计）货车正以
40km／h的速度开往乙地，当行驶1小时，忽然接到通知；前方连降暴雨，造成水位以每小时0．25m的速度持续上涨（货车接到通知时水位在CD处，当水位到达最高点O时，禁止车辆通行）试问：如果货车按原来速度行驶，能否安全通过此桥？若能，请说明理由，若不能，要使货车安全通过此桥，速度应超过每小时多少千米？
7.如图1－2－47，隧道的截面由抛物线AED和矩形ABCD构成，矩形的长BC为
8m，宽
AB为
2m，以
BC所在的直线为x轴，线段BC的中垂线为y轴，建立平面直角坐标系，y轴是抛物线的对称轴，顶点
E到坐标原点O的距离为6m。
（1）求抛物线的解析式；
（2）如果该隧道内设双行道，现有一辆货运卡车高4.2m，宽2.4m，这辆货运卡车能否通过该隧道？通过计算说明你的结论。