3.3 垂径定理课件

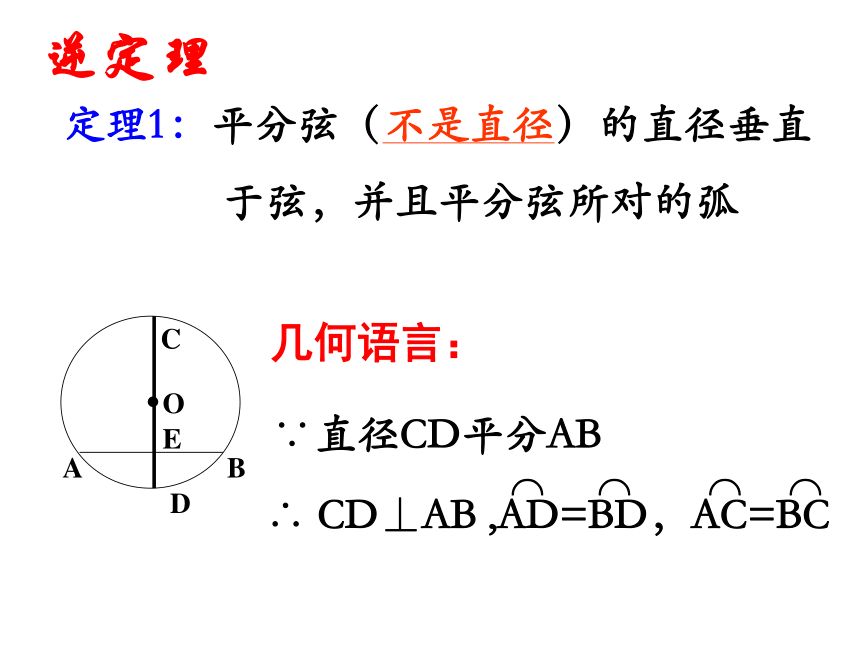
课件21张PPT。3.3垂径定理（2）复习回顾1.什么是垂径定理？ 垂直于弦的直径平分这条弦，并且平分弦所对的弧2.垂径定理的题设与结论分别是什么？题 设：垂直于弦的直径结论1：直径平分弦（不是直径）结论2：直径平分弧已知：⊙O的直径CD交弦AB（不是直径）于点E，且AE=BE.求证：CD⊥AB，AD＝BD，AC＝BC.证明：连结OA，OB，则OA=OB∴△AOB是等腰三角形∵AE=BE,∴CD⊥AB（等腰三角形三线合一）逆定理定理1：平分弦（不是直径）的直径垂直
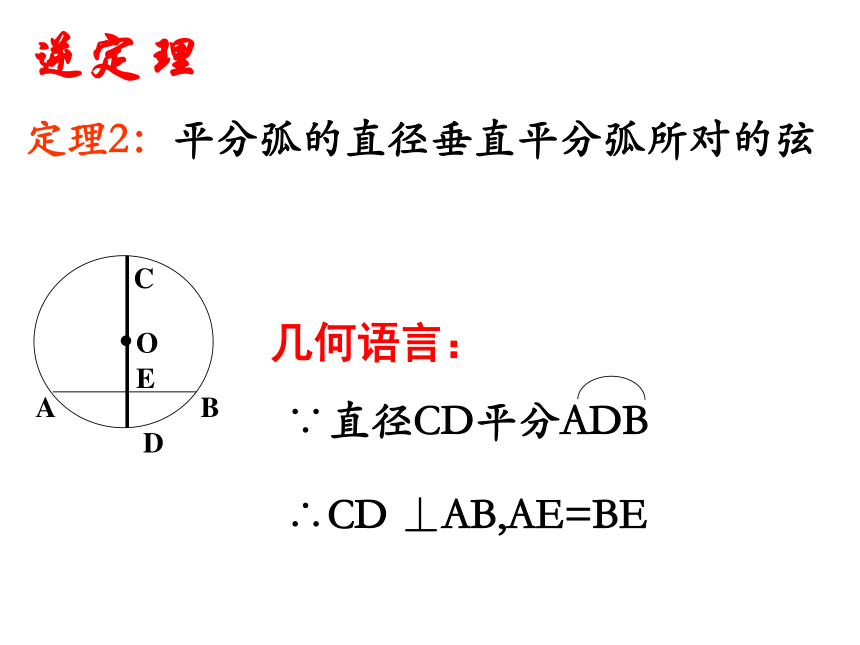
于弦，并且平分弦所对的弧几何语言：∵直径CD平分AB已知：CD是⊙O的直径，且AD=BD。⌒⌒求证：CD⊥AB，AE=BE∴点A与B重合即A,B关于直线CD对折∴ CD⊥AB，AE=BE逆定理定理2：平分弧的直径垂直平分弧所对的弦几何语言：∴CD ⊥AB,AE=BE 垂直于弦的直径平分这条弦，并且平分弦所对的弧逆定理定理1：平分弦（不是直径）的直径垂直
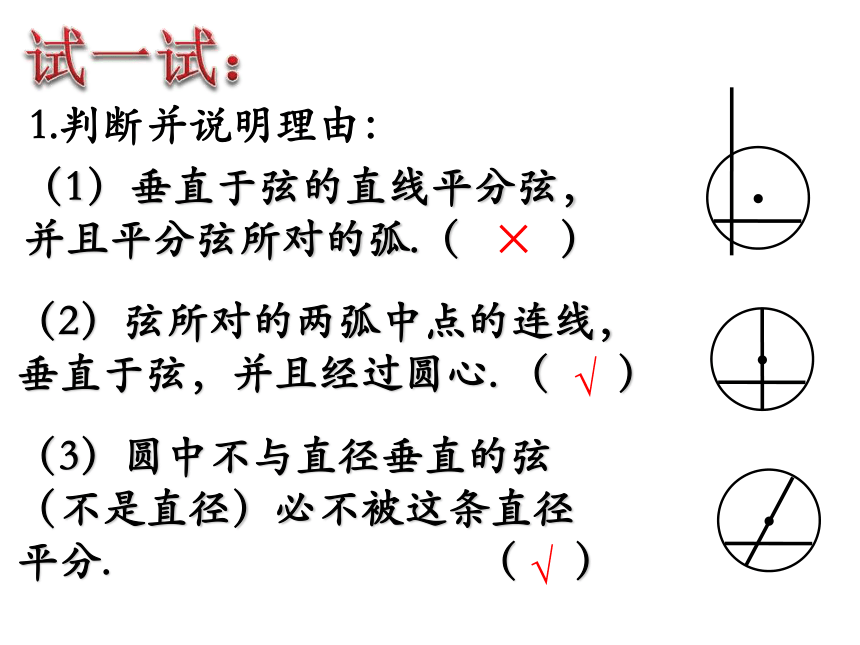
于弦，并且平分弦所对的弧定理2：平分弧的直径垂直平分弧所对的弦垂径定理试一试：1.判断并说明理由：（1）垂直于弦的直线平分弦，并且平分弦所对的弧.（ ）×（2）弦所对的两弧中点的连线，垂直于弦，并且经过圆心. （ ）√（3）圆中不与直径垂直的弦（不是直径）必不被这条直径平分. （ ）√（4）平分弦的直径垂直于弦，并且平分弦所对的两条弧（ ）（5）圆内两条非直径的弦不能互相平分. （ ）√×（6）平分弦的直径，平分这条弦所对的弧。 （ ）×（7）平分弦的直线，必定过圆心。 （ ）×（8）弦的垂直平分线一定是圆的直径。 （ ）（9）平分弧的直线，平分这条弧所对的弦。 （ ）（10）弦垂直于直径，这条直径就被弦平分。 （ ）×××2.已知，如图，在以点O为圆心的两个圆中，大圆的弦AB和小圆交于点C,D。
求证：AC=BD.E3.已知：如图,⊙O的直径PQ分别交弦AB,CD于点M,N,AM=BM,AB∥CD.
求证：DN=CN.BACDOPQMN例1.已知赵州桥的跨径（桥拱圆弧所对弦的长）为37.02m，拱高（桥拱圆弧中点到弦的距离）为7.23m。求赵州桥的桥拱圆弧的半径（精确到0.1m）.BACDOR37.027.231.如图，一圆弧形钢梁的拱高为8m，跨径为40m，求钢梁圆弧的半径长。BA408做一做：例2.已知⊙O的半径为5cm，弦AB ∥CD, AB=6cm,CD=8cm.求AB与CD之间的距离。课堂小结: 解决有关弦的问题，经常是过圆心作弦的垂线，或作垂直于弦的直径，连结半径等辅助线，为应用垂径定理创造条件。能力提升练习：1.已知：如图，M是弧AB的中点，过点M的弦MN交AB于点C，设⊙O的半径为4cm,mn=4 cm.
(1)求圆心到弦MN的距离。
(2)求∠ACM的度数。BACOMND2.在半径为1的⊙O中，弦AB,AC的长分别为 和 ，求∠BAC的度数。BACOC3.某条公路隧道的形状如图，半圆拱的圆心离地面2m，半径为1.5m，一辆高3m，宽为2.3m的集装箱卡车能顺利通过这个隧道吗？如果要使高度不超过4m，宽为2.3m的大货车也能顺利通过这个隧道，且不改变圆心到地面的距离，半圆拱的半径至少为多少米？21.5OAB4.已知，如图，抛物线y=ax2+bx+c经过A（1,0），B（5,0），C（0,5）三点。（1）求抛物线的函数关系式。yxCOABE（2）若过点C的直线y=kx+b与抛物线相交于点E（4，m），请求出△BCE的面积S的值。（3）在抛物线上找出所有使得△ABP为等腰三角形的P点，一共有几个P点。P1P2P3P4P5P6P7再见！