2.8 直角三角形全等的判定 课件 (共21张PPT)
文档属性
| 名称 | 2.8 直角三角形全等的判定 课件 (共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-09 18:21:29 | ||
图片预览







文档简介
课件21张PPT。2.8 直角三角形全等的判定 问题1 如图,舞台背景的形状是两个直角三角形,
为了美观,工作人员想知道这两个直角三角形是否全
等,但每个三角形都有一条直角边被花盆遮住无法测
量.你能帮工作人员想个办法吗? (1)如果用直尺和量角器两种工具,你能解决这个
问题吗?探究新知 (2)如果只用直尺,你能解决这个问题吗? 问题1 如图,舞台背景的形状是两个直角三角形,
为了美观,工作人员想知道这两个直角三角形是否全
等,但每个三角形都有一条直角边被花盆遮住无法测
量.你能帮工作人员想个办法吗? 问题2 任意画一个Rt△ABC,使∠C =90°,再画
一个Rt△A'B'C',使∠C'=90°,B'C'=BC,
A'B'=AB,然后把画好的Rt△A'B'C'剪下来放到
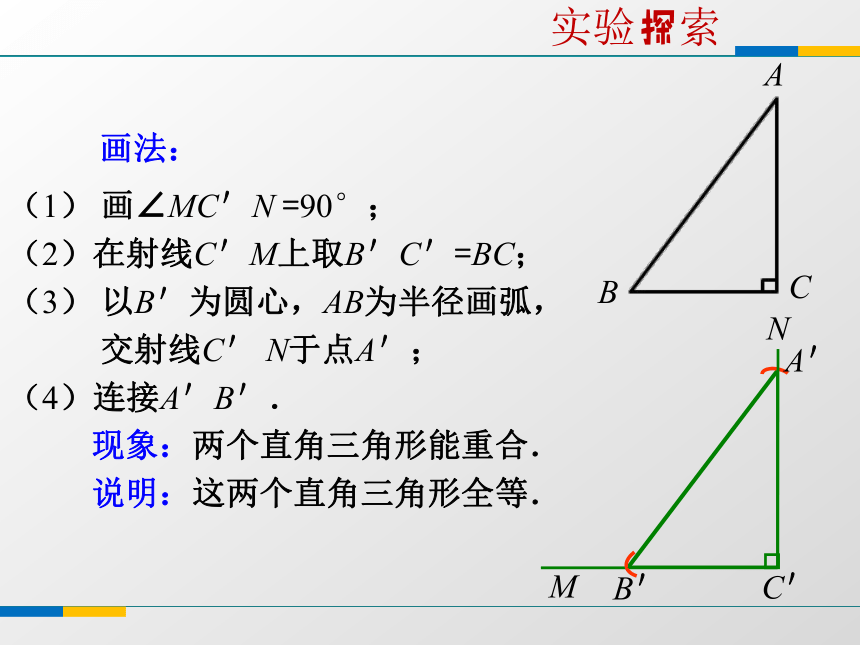
Rt△ABC上,你发现了什么?Rt△ABC ≌ Rt△A'B'C'(1) 画∠MC'N =90°;
(2)在射线C'M上取B'C'=BC;
(3) 以B'为圆心,AB为半径画弧,
交射线C' N于点A';
(4)连接A'B'. 现象:两个直角三角形能重合.
说明:这两个直角三角形全等. 画法:实验探索 斜边和一条直角边分别相等的两个直角三角形全等
(简写为“斜边、直角边”或“HL”).几何语言:
∵ 在Rt△ABC 和 Rt△A'B'C'中,
AB =A'B',
BC =B'C',
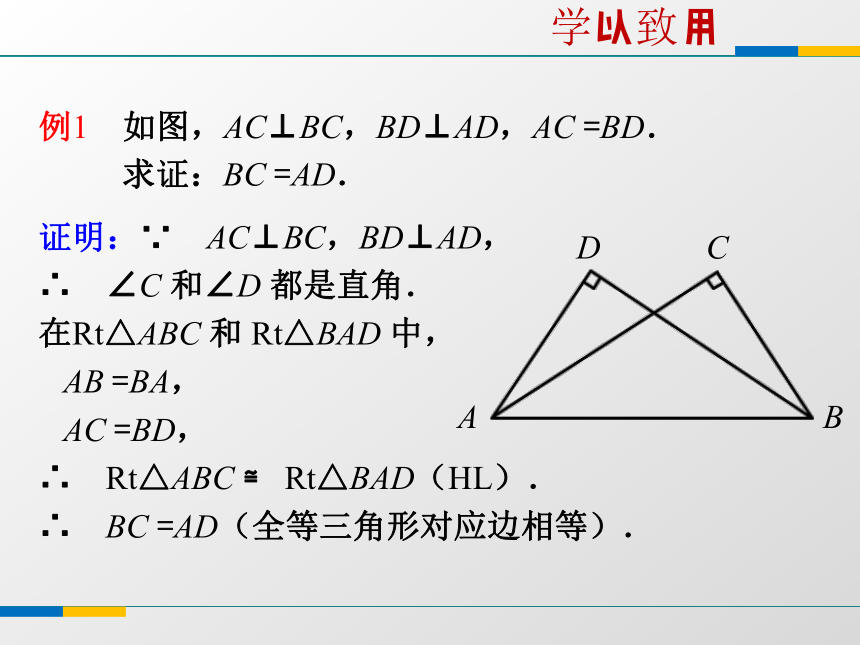
∴ Rt△ABC ≌ Rt△A'B'C'(HL) .探究归纳证明:∵ AC⊥BC,BD⊥AD,
∴ ∠C 和∠D 都是直角.
在Rt△ABC 和 Rt△BAD 中,
AB =BA,
AC =BD,
∴ Rt△ABC ≌ Rt△BAD(HL).
∴ BC =AD(全等三角形对应边相等).例1 如图,AC⊥BC,BD⊥AD,AC =BD.
求证:BC =AD.学以致用 变式1 如图,AC⊥BC,BD⊥AD,要证△ABC
≌△BAD,需要添加一个什么条件?请说明理由.
(1) ( );
(2) ( );
(3) ( );
(4) ( ).AD = BCAC = BD∠DAB = ∠CBA∠DBA = ∠CABHLHLAASAAS变式训练 问题3 如图,要在S 区建一个广告牌P,使它到
两条高速公路的距离相等,离两条公路交叉处500 m,
请你帮忙设计一下,这个广告牌P 应建于何处(在图上
标出它的位置,比例尺为1:20 000)? 继续探究 问题4 交换角的平分线的性质中的已知和结论,
你能得到什么结论,这个新结论正确吗?在一个角的内部, 且到角的两边距离相等的点在这个角的平分线上.如图,
∵ PD=PE, PD⊥OA, PE⊥OB,
垂足分别是D, E(已知),
∴点P在∠AOB的平分线上.
(在一个角的内部,且到角的两边距离相等的点在这个角的平分线上). 这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.角的内部到角的两边距离相等的点在角的平分线上.探究归纳已知: 如图所示, PD=PE, PD⊥OA,
PE⊥OB, 垂足分别是D,E.
求证: 点P在∠AOB的平分线上.证明:∵ PD⊥OA ,PE⊥OB
∴ △POD和△POE都是Rt△
∵ PD=PE,OP=OP
∴ Rt△POD≌Rt△POE(HL)
∴ ∠POD= ∠POE
∴ OC是∠AOB的平分线
∴ 点P在∠AOB的平分线上探索证明例2 如图, △ABC的角平分线BM, CN相交于点P, 求证:点P到三边AB、BC、CA 的距离相等.证明:过点P作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F
∵ BM为△ABC的角平分线
∴PD=PE
同理, PE=PF.
∴PD=PE=PF
即点P到三边AB、BC、CA的距离相等学以致用X 1.判断题:
(1)如图,若QM =QN,则OQ 平分∠AOB;( )课堂练习X 1.判断题:
(2)如图,若QM⊥OA 于M,QN⊥OB 于N,则OQ是∠AOB 的平分线; ( ) √ 1.判断题:
(3)已知:Q 到OA 的距离等于2 cm, 且Q 到OB 距离等于2 cm,则Q 在∠AOB 的平分线上.( )2. 如图,有两个长度相同的滑梯,左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,两个滑梯 的倾斜角∠ABC 和∠DFE 的大小有什么关系?为什么?∠ABC +∠DFE =90° 证明:∵ AC⊥AB,DE⊥DF,
∴ ∠CAB 和∠FDE 都是直角.
在Rt△ABC 和 Rt△DEF 中,∴ Rt△ABC ≌ Rt△DEF(HL). 2. 如图,有两个长度相同的滑梯,左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,两个滑梯 的倾斜角∠ABC 和∠DFE 的大小有什么关系?为什么?证明:∴ ∠ABC =∠DEF
(全等三角形对应角相等).
∵ ∠DEF +∠DFE =90°,
∴ ∠ABC +∠DFE =90°. 2. 如图,有两个长度相同的滑梯,左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,两个滑梯 的倾斜角∠ABC 和∠DFE 的大小有什么关系?为什么?(1)“HL”判定方法应满足什么条件?与之前所学
的四种判定方法有什么不同?
(2)判定两个直角三角形全等有哪些方法?课堂小结(3)角平分线的性质定理的掌握与应用教科书作业题第2、3、4题.课后作业
为了美观,工作人员想知道这两个直角三角形是否全
等,但每个三角形都有一条直角边被花盆遮住无法测
量.你能帮工作人员想个办法吗? (1)如果用直尺和量角器两种工具,你能解决这个
问题吗?探究新知 (2)如果只用直尺,你能解决这个问题吗? 问题1 如图,舞台背景的形状是两个直角三角形,
为了美观,工作人员想知道这两个直角三角形是否全
等,但每个三角形都有一条直角边被花盆遮住无法测
量.你能帮工作人员想个办法吗? 问题2 任意画一个Rt△ABC,使∠C =90°,再画
一个Rt△A'B'C',使∠C'=90°,B'C'=BC,
A'B'=AB,然后把画好的Rt△A'B'C'剪下来放到
Rt△ABC上,你发现了什么?Rt△ABC ≌ Rt△A'B'C'(1) 画∠MC'N =90°;
(2)在射线C'M上取B'C'=BC;
(3) 以B'为圆心,AB为半径画弧,
交射线C' N于点A';
(4)连接A'B'. 现象:两个直角三角形能重合.
说明:这两个直角三角形全等. 画法:实验探索 斜边和一条直角边分别相等的两个直角三角形全等
(简写为“斜边、直角边”或“HL”).几何语言:
∵ 在Rt△ABC 和 Rt△A'B'C'中,
AB =A'B',
BC =B'C',
∴ Rt△ABC ≌ Rt△A'B'C'(HL) .探究归纳证明:∵ AC⊥BC,BD⊥AD,
∴ ∠C 和∠D 都是直角.
在Rt△ABC 和 Rt△BAD 中,
AB =BA,
AC =BD,
∴ Rt△ABC ≌ Rt△BAD(HL).
∴ BC =AD(全等三角形对应边相等).例1 如图,AC⊥BC,BD⊥AD,AC =BD.
求证:BC =AD.学以致用 变式1 如图,AC⊥BC,BD⊥AD,要证△ABC
≌△BAD,需要添加一个什么条件?请说明理由.
(1) ( );
(2) ( );
(3) ( );
(4) ( ).AD = BCAC = BD∠DAB = ∠CBA∠DBA = ∠CABHLHLAASAAS变式训练 问题3 如图,要在S 区建一个广告牌P,使它到
两条高速公路的距离相等,离两条公路交叉处500 m,
请你帮忙设计一下,这个广告牌P 应建于何处(在图上
标出它的位置,比例尺为1:20 000)? 继续探究 问题4 交换角的平分线的性质中的已知和结论,
你能得到什么结论,这个新结论正确吗?在一个角的内部, 且到角的两边距离相等的点在这个角的平分线上.如图,
∵ PD=PE, PD⊥OA, PE⊥OB,
垂足分别是D, E(已知),
∴点P在∠AOB的平分线上.
(在一个角的内部,且到角的两边距离相等的点在这个角的平分线上). 这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.角的内部到角的两边距离相等的点在角的平分线上.探究归纳已知: 如图所示, PD=PE, PD⊥OA,
PE⊥OB, 垂足分别是D,E.
求证: 点P在∠AOB的平分线上.证明:∵ PD⊥OA ,PE⊥OB
∴ △POD和△POE都是Rt△
∵ PD=PE,OP=OP
∴ Rt△POD≌Rt△POE(HL)
∴ ∠POD= ∠POE
∴ OC是∠AOB的平分线
∴ 点P在∠AOB的平分线上探索证明例2 如图, △ABC的角平分线BM, CN相交于点P, 求证:点P到三边AB、BC、CA 的距离相等.证明:过点P作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F
∵ BM为△ABC的角平分线
∴PD=PE
同理, PE=PF.
∴PD=PE=PF
即点P到三边AB、BC、CA的距离相等学以致用X 1.判断题:
(1)如图,若QM =QN,则OQ 平分∠AOB;( )课堂练习X 1.判断题:
(2)如图,若QM⊥OA 于M,QN⊥OB 于N,则OQ是∠AOB 的平分线; ( ) √ 1.判断题:
(3)已知:Q 到OA 的距离等于2 cm, 且Q 到OB 距离等于2 cm,则Q 在∠AOB 的平分线上.( )2. 如图,有两个长度相同的滑梯,左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,两个滑梯 的倾斜角∠ABC 和∠DFE 的大小有什么关系?为什么?∠ABC +∠DFE =90° 证明:∵ AC⊥AB,DE⊥DF,
∴ ∠CAB 和∠FDE 都是直角.
在Rt△ABC 和 Rt△DEF 中,∴ Rt△ABC ≌ Rt△DEF(HL). 2. 如图,有两个长度相同的滑梯,左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,两个滑梯 的倾斜角∠ABC 和∠DFE 的大小有什么关系?为什么?证明:∴ ∠ABC =∠DEF
(全等三角形对应角相等).
∵ ∠DEF +∠DFE =90°,
∴ ∠ABC +∠DFE =90°. 2. 如图,有两个长度相同的滑梯,左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,两个滑梯 的倾斜角∠ABC 和∠DFE 的大小有什么关系?为什么?(1)“HL”判定方法应满足什么条件?与之前所学
的四种判定方法有什么不同?
(2)判定两个直角三角形全等有哪些方法?课堂小结(3)角平分线的性质定理的掌握与应用教科书作业题第2、3、4题.课后作业
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
