1.2 二次函数图象间的关系 课件 (共19张PPT)
文档属性
| 名称 | 1.2 二次函数图象间的关系 课件 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-10 07:57:28 | ||
图片预览





文档简介
课件19张PPT。1.2 二次函数图象间的关系y=ax2+ky=a(x-h)^2+ky=a(x-h)^2y=ax2 问题1
(1)二次函数 y = ax 2 的图象是什么?
(2)它具有怎样的图象特征?
(3)你是怎么研究的?回顾探究 问题2
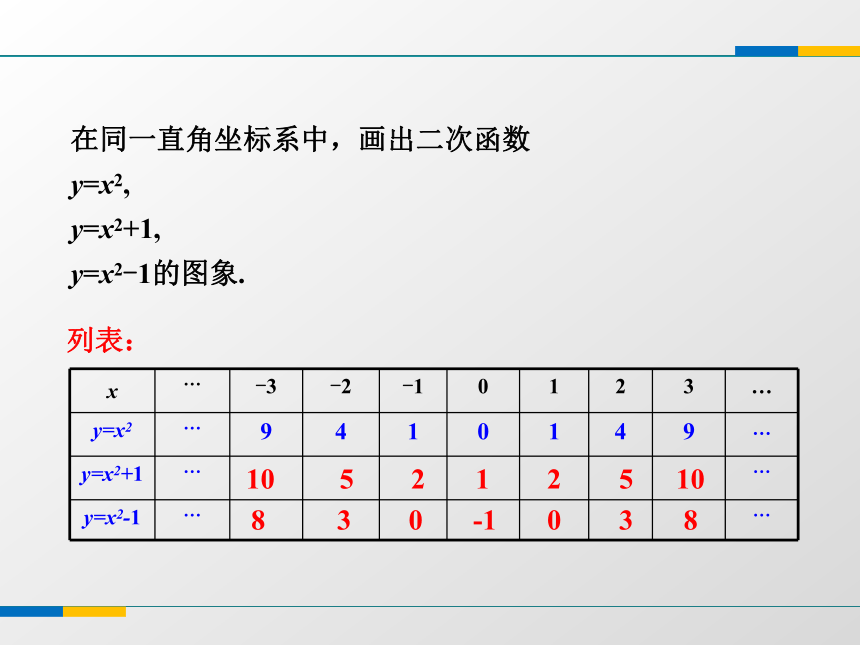
类比 y = ax 2 的研究内容和研究方法,画出二次函数y = x 2 + 1, y = x 2 - 1 的图象,并探究它们图象间的关系.在同一直角坐标系中,画出二次函数
y=x2,
y=x2+1,
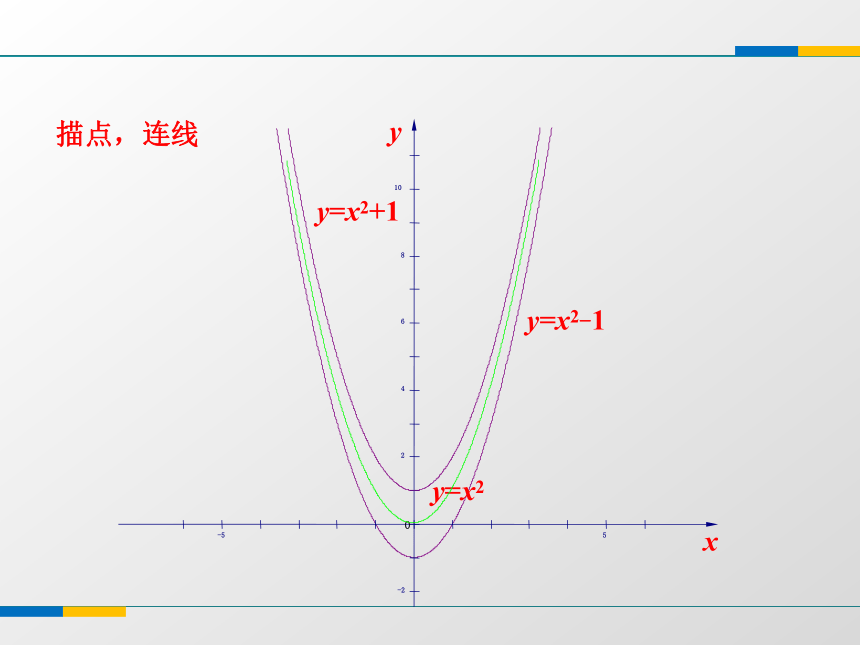
y=x2-1的图象.列表:10 5 2 1 2 5 108 3 0 -1 0 3 8 y=x2+1108642-2-55xy y=x2-1y=x2O描点,连线抛物线 y = ax 2 + k 与抛物线 y = ax 2图象间有什么关系?归纳:
当 k>0 时,把抛物线 y = ax 2 向上平移 k 个单位,就得到抛物线 y = ax 2 + k;
当 k<0 时,把抛物线 y = ax 2 向下平移|k|个单位,就得到抛物线 y = ax 2 + k.探究追问 在同一直角坐标系中,画出二次函数 的图象,并探究它们图象间的关系.继续探究-2-8-4.5-200-2-8-4.5-2 抛物线 与抛物线 图象间有什么关系? 抛物线 与抛物线 y = ax 2 有什么关系?归纳:
当 h>0 时,把抛物线 y = ax 2 向右平移 h 个单位长度,就得到抛物线 ;
当 h<0 时,把 y = ax 2 向左平移|h|个单位长度,就得到抛物线 .探究归纳例2 对于二次函数 请回答下列问题:1) 把函数 的图象作怎样的平移变换,就能得到函数 的图象.2)说出函数 的图象的顶点坐标和对称轴.向右平移4个单位 顶点坐标是(4,0)对称轴是直线 x=4例题探究 你能说出 的图象特征吗?它与抛物线 有什么关系?你能说出
的图象特征吗?类比探究向左平移1个单位向下平移1个单位向左平移1个单位向下平移1个单位平移方法1:平移方法2:x=-1抛物线 有什么关系? 抛物线 有如下特点:
(1)当 a>0 时,开口向上;当 a<0 时,开口向下.
(2)对称轴为直线 x = h.
(3)顶点坐标(h,k).巩固训练1. 按下列要求求出二次函数的解析式:
(1)已知抛物线y=a(x-h)2经过点(-3,2)(-1,0),求该抛物线线的解析式 . (2)形状与y=-2(x+3)2的图象形状相同,但开口方向不同,顶点坐标是(1,0)的抛物线解析式.2. 要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为 1 m 处达到最高,高度为 3 m,水柱落地处离池中心 3 m,水管应多长?C(3,0)B(1,3) A解: 如图建立直角坐标系,点(1,3)是图中这段抛物线的顶点.因此可设这段抛物线对应的函数是∵这段抛物线经过点(3,0)∴ 0=a(3-1)2+3解得:因此抛物线的解析式为:y=a(x-1)2+3 (0≤x≤3)当x=0时, y=2.25∴水管长应为2.25m. (1)本节课学了哪些主要内容?
(2)抛物线y = ax 2 ,y = ax 2 + k ,y=a(x-h)^2,
y=a(x-h)^2+k之间的区别与联系?课堂小结 教科书习题A组 第 1,2,3题.课后作业
(1)二次函数 y = ax 2 的图象是什么?
(2)它具有怎样的图象特征?
(3)你是怎么研究的?回顾探究 问题2
类比 y = ax 2 的研究内容和研究方法,画出二次函数y = x 2 + 1, y = x 2 - 1 的图象,并探究它们图象间的关系.在同一直角坐标系中,画出二次函数
y=x2,
y=x2+1,
y=x2-1的图象.列表:10 5 2 1 2 5 108 3 0 -1 0 3 8 y=x2+1108642-2-55xy y=x2-1y=x2O描点,连线抛物线 y = ax 2 + k 与抛物线 y = ax 2图象间有什么关系?归纳:
当 k>0 时,把抛物线 y = ax 2 向上平移 k 个单位,就得到抛物线 y = ax 2 + k;
当 k<0 时,把抛物线 y = ax 2 向下平移|k|个单位,就得到抛物线 y = ax 2 + k.探究追问 在同一直角坐标系中,画出二次函数 的图象,并探究它们图象间的关系.继续探究-2-8-4.5-200-2-8-4.5-2 抛物线 与抛物线 图象间有什么关系? 抛物线 与抛物线 y = ax 2 有什么关系?归纳:
当 h>0 时,把抛物线 y = ax 2 向右平移 h 个单位长度,就得到抛物线 ;
当 h<0 时,把 y = ax 2 向左平移|h|个单位长度,就得到抛物线 .探究归纳例2 对于二次函数 请回答下列问题:1) 把函数 的图象作怎样的平移变换,就能得到函数 的图象.2)说出函数 的图象的顶点坐标和对称轴.向右平移4个单位 顶点坐标是(4,0)对称轴是直线 x=4例题探究 你能说出 的图象特征吗?它与抛物线 有什么关系?你能说出
的图象特征吗?类比探究向左平移1个单位向下平移1个单位向左平移1个单位向下平移1个单位平移方法1:平移方法2:x=-1抛物线 有什么关系? 抛物线 有如下特点:
(1)当 a>0 时,开口向上;当 a<0 时,开口向下.
(2)对称轴为直线 x = h.
(3)顶点坐标(h,k).巩固训练1. 按下列要求求出二次函数的解析式:
(1)已知抛物线y=a(x-h)2经过点(-3,2)(-1,0),求该抛物线线的解析式 . (2)形状与y=-2(x+3)2的图象形状相同,但开口方向不同,顶点坐标是(1,0)的抛物线解析式.2. 要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为 1 m 处达到最高,高度为 3 m,水柱落地处离池中心 3 m,水管应多长?C(3,0)B(1,3) A解: 如图建立直角坐标系,点(1,3)是图中这段抛物线的顶点.因此可设这段抛物线对应的函数是∵这段抛物线经过点(3,0)∴ 0=a(3-1)2+3解得:因此抛物线的解析式为:y=a(x-1)2+3 (0≤x≤3)当x=0时, y=2.25∴水管长应为2.25m. (1)本节课学了哪些主要内容?
(2)抛物线y = ax 2 ,y = ax 2 + k ,y=a(x-h)^2,
y=a(x-h)^2+k之间的区别与联系?课堂小结 教科书习题A组 第 1,2,3题.课后作业
同课章节目录
