2.4 概率的简单应用 课件(共15张PPT)
文档属性
| 名称 | 2.4 概率的简单应用 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-10 08:19:50 | ||
图片预览




文档简介
课件15张PPT。2.4 概率的简单应用1.什么叫概率?事件发生的可能性的大小叫这一事件发生的概率.2.概率的计算公式:若事件发生的所有可能结果总数为n,事件A发生的可能结果数为m,则P(A)=3.估计概率在实际生活中,我们常用频率来估计概率,在大量重复的实验中发现频率接近于哪个数,把这个数作为概率.学科网 旧知回顾1. 如果有人买了彩票,一定希望知道中奖的概率有多大.
那么怎么样来估计中奖的概率呢?2. 出门旅行的人希望知道乘坐哪一种交通工具发生事故的可能性较小? 概率与人们生活密切相关,在生活,生产和科研等各个领域都有着广泛的应用.例1. 某商场举办有奖销售活动,每张奖券获奖的可能性相同,以每10000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖100个,问1张奖券中一等奖的概率是多少?中奖的概率是多少?解: 因为10000张奖券中能中一等奖的张数是10张, 所以1张奖券中一等奖的概率是:
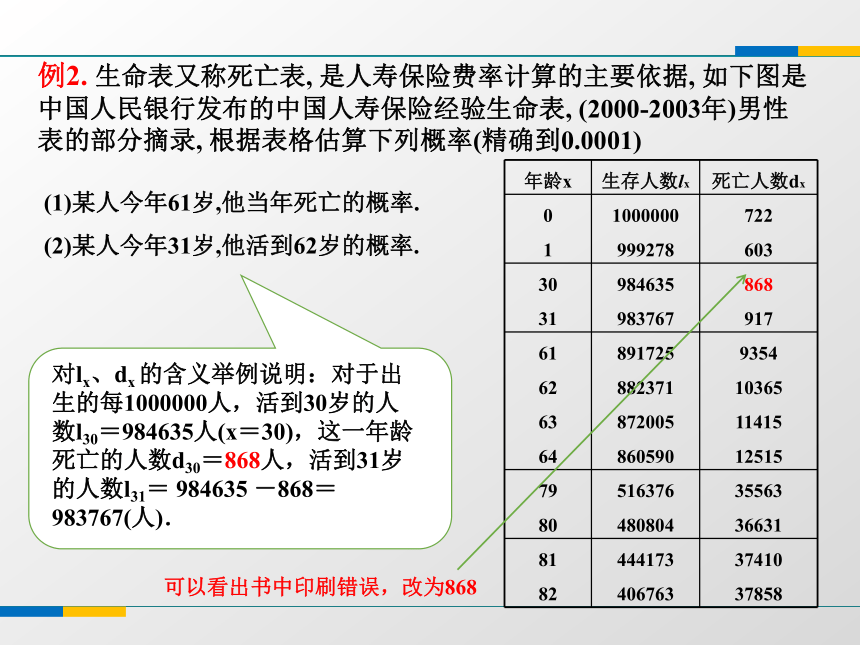
又因为10000张奖券中能中奖的奖券总数是1+10+100=111(张)所以1张奖券中奖的概率是 例题探究例2. 生命表又称死亡表, 是人寿保险费率计算的主要依据, 如下图是中国人民银行发布的中国人寿保险经验生命表, (2000-2003年)男性表的部分摘录, 根据表格估算下列概率(精确到0.0001)(1)某人今年61岁,他当年死亡的概率.
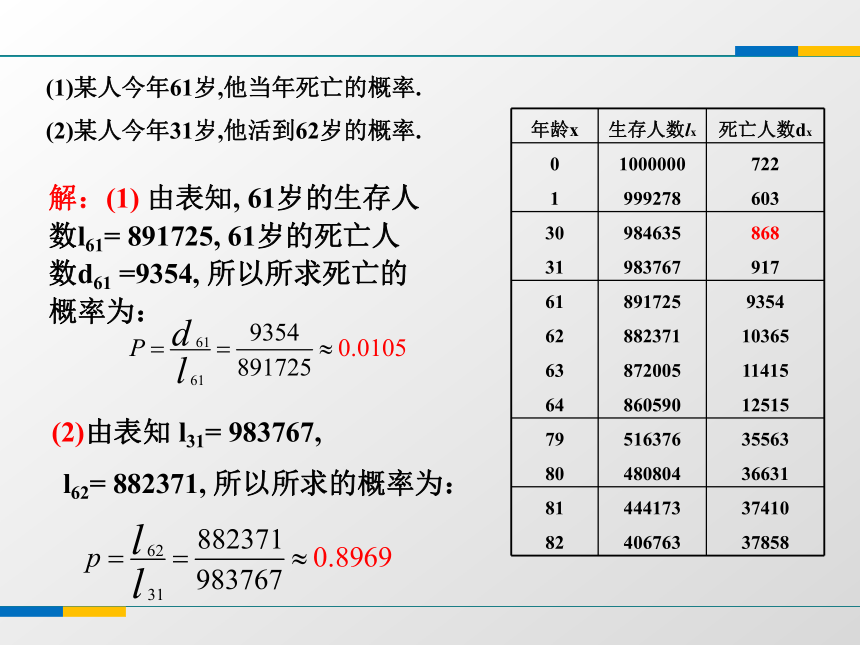
(2)某人今年31岁,他活到62岁的概率.可以看出书中印刷错误,改为868(1)某人今年61岁,他当年死亡的概率.
(2)某人今年31岁,他活到62岁的概率.解:(1) 由表知, 61岁的生存人数l61= 891725, 61岁的死亡人数d61 =9354, 所以所求死亡的概率为:(2)由表知 l31= 983767,
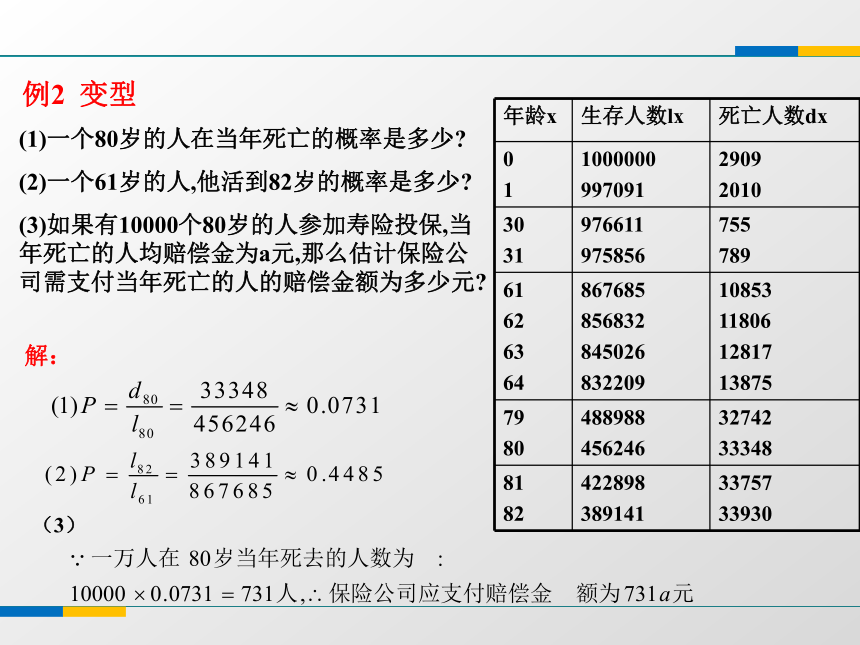
l62= 882371, 所以所求的概率为:(1)一个80岁的人在当年死亡的概率是多少?
(2)一个61岁的人,他活到82岁的概率是多少?
(3)如果有10000个80岁的人参加寿险投保,当年死亡的人均赔偿金为a元,那么估计保险公司需支付当年死亡的人的赔偿金额为多少元?例2 变型解:(3)1. 九年级三班同学作了关于私家车乘坐人数的统计, 在100辆私家车中,统计结果如下表: 根据以上结果,估计抽查一辆私家车而它载有超过2名乘客的概率是多少?课堂练习2. 有一种游戏,班级里每位同学及数学老师的手中都有1点,2点,3点三张扑克,游戏规则一:每位同学任意抽一张,数学老师也抽一张,如果同学抽到的点数和老师抽到的点数相同,那么这位同学就获得一份小礼物;游戏规则二:每位同学任意抽两张,数学老师也抽两张,如果同学抽到的这两张点数和老师抽到的两张点数相同,那么这位同学获得一份小礼物.问:
(1)游戏规则一,每位同学获得小礼物的概率是多少?
(2)游戏规则二,每位同学获得小礼物的概率是多少?1. 现有5根小木棒,长度分别为:2、3、4、5、7(单位:cm),从中任意取出3根,
(1)列出所选的3根小木棒的所有可能情况;
(2)如果用这3根小木棒首尾顺次相接,求它们能搭成三角形的概率.解:(1)根据题意可得:所选的3根小木棒的所有可能情况为:(2、3、4),(2、3、5),(2、3、7),(2、4、5),(2、4、7),(2、5、7),(3、4、5),(3、4、7),(3、5、7),(4、5、7);(2)∵能搭成三角形的结果有: (2、3、4),(2、4、5),
(3、4、5),(3、5、7),(4、5、7) 共5种巩固提升2. 有一组互不全等的三角形,它们的边长均为整数,每个三角形有两条边的长分别为5和7.
(1)请写出其中一个三角形的第三边的长;
(2)设组中最多有n个三角形,求n的值;
(3)当这组三角形个数最多时,从中任取一个,求该三角形周长为偶数的概率.解:(1)设三角形的第三边为x,
∵每个三角形有两条边的长分别为5和7,
∴7﹣5<x<5+7,∴2<x<12,
∴其中一个三角形的第三边的长可以为10.(2)∵ 2<x<12,它们的边长均为整数,
∴ x=3,4,5,6,7,8,9,10,11,
∴ 组中最多有9个三角形,∴n=9;(3)∵当x=4,6,8,10时,该三角形周长为偶数,
∴该三角形周长为偶数的概率是3. 已知甲同学手中藏有三张分别标有数字 , ,1的卡片,
乙同学手中藏有三张分别标有数字1,3,2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
(1)请你用树形图或列表法列出所有可能的结果.
(2)现制定这样一个游戏规则:若所选出的a,b能使得
有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请你用概率知识解释.甲1乙132∴(a,b)取值结果共有9种 ∴P(甲获胜)= P(Δ>0)=
>P(乙获胜) =(2)
∵Δ=b2-4a与对应(1)中的结果为:-1、2、7、0、3、8、-3、0、5 所以不公平4. 小明和小刚玩“石头、剪刀、布”的游戏,每一局游戏双方各自随机做出“石头”、“剪刀”、“布”三种手势的一种,规定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,相同的手势是和局.(1)用树形图或列表法计算在一局游戏中两人获胜的概率各是多少?解:(1)画树状图得: ∵总共有9种情况,每一种出现的机会均等,每人获胜的情形都是3种, ∴两人获胜的概率都是(2)由(1)可知,一局游戏每人胜、负、和的机会均等,都为 ,任选其中一人的情形可画树状图得:∵总共有9种情况,每一种出现的机会均等,当出现(胜,胜)或(负,负)这两种情形时,赢家产生.∴两局游戏能确定赢家的概率为:4. 小明和小刚玩“石头、剪刀、布”的游戏,每一局游戏双方各自随机做出“石头”、“剪刀”、“布”三种手势的一种,规定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,相同的手势是和局.
(2)如果两人约定:只要谁率先胜两局,就成了游戏的赢家.
用树形图或列表法求只进行两局游戏便能确定赢家的概率. 本节课你学到了什么?课堂小结
那么怎么样来估计中奖的概率呢?2. 出门旅行的人希望知道乘坐哪一种交通工具发生事故的可能性较小? 概率与人们生活密切相关,在生活,生产和科研等各个领域都有着广泛的应用.例1. 某商场举办有奖销售活动,每张奖券获奖的可能性相同,以每10000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖100个,问1张奖券中一等奖的概率是多少?中奖的概率是多少?解: 因为10000张奖券中能中一等奖的张数是10张, 所以1张奖券中一等奖的概率是:
又因为10000张奖券中能中奖的奖券总数是1+10+100=111(张)所以1张奖券中奖的概率是 例题探究例2. 生命表又称死亡表, 是人寿保险费率计算的主要依据, 如下图是中国人民银行发布的中国人寿保险经验生命表, (2000-2003年)男性表的部分摘录, 根据表格估算下列概率(精确到0.0001)(1)某人今年61岁,他当年死亡的概率.
(2)某人今年31岁,他活到62岁的概率.可以看出书中印刷错误,改为868(1)某人今年61岁,他当年死亡的概率.
(2)某人今年31岁,他活到62岁的概率.解:(1) 由表知, 61岁的生存人数l61= 891725, 61岁的死亡人数d61 =9354, 所以所求死亡的概率为:(2)由表知 l31= 983767,
l62= 882371, 所以所求的概率为:(1)一个80岁的人在当年死亡的概率是多少?
(2)一个61岁的人,他活到82岁的概率是多少?
(3)如果有10000个80岁的人参加寿险投保,当年死亡的人均赔偿金为a元,那么估计保险公司需支付当年死亡的人的赔偿金额为多少元?例2 变型解:(3)1. 九年级三班同学作了关于私家车乘坐人数的统计, 在100辆私家车中,统计结果如下表: 根据以上结果,估计抽查一辆私家车而它载有超过2名乘客的概率是多少?课堂练习2. 有一种游戏,班级里每位同学及数学老师的手中都有1点,2点,3点三张扑克,游戏规则一:每位同学任意抽一张,数学老师也抽一张,如果同学抽到的点数和老师抽到的点数相同,那么这位同学就获得一份小礼物;游戏规则二:每位同学任意抽两张,数学老师也抽两张,如果同学抽到的这两张点数和老师抽到的两张点数相同,那么这位同学获得一份小礼物.问:
(1)游戏规则一,每位同学获得小礼物的概率是多少?
(2)游戏规则二,每位同学获得小礼物的概率是多少?1. 现有5根小木棒,长度分别为:2、3、4、5、7(单位:cm),从中任意取出3根,
(1)列出所选的3根小木棒的所有可能情况;
(2)如果用这3根小木棒首尾顺次相接,求它们能搭成三角形的概率.解:(1)根据题意可得:所选的3根小木棒的所有可能情况为:(2、3、4),(2、3、5),(2、3、7),(2、4、5),(2、4、7),(2、5、7),(3、4、5),(3、4、7),(3、5、7),(4、5、7);(2)∵能搭成三角形的结果有: (2、3、4),(2、4、5),
(3、4、5),(3、5、7),(4、5、7) 共5种巩固提升2. 有一组互不全等的三角形,它们的边长均为整数,每个三角形有两条边的长分别为5和7.
(1)请写出其中一个三角形的第三边的长;
(2)设组中最多有n个三角形,求n的值;
(3)当这组三角形个数最多时,从中任取一个,求该三角形周长为偶数的概率.解:(1)设三角形的第三边为x,
∵每个三角形有两条边的长分别为5和7,
∴7﹣5<x<5+7,∴2<x<12,
∴其中一个三角形的第三边的长可以为10.(2)∵ 2<x<12,它们的边长均为整数,
∴ x=3,4,5,6,7,8,9,10,11,
∴ 组中最多有9个三角形,∴n=9;(3)∵当x=4,6,8,10时,该三角形周长为偶数,
∴该三角形周长为偶数的概率是3. 已知甲同学手中藏有三张分别标有数字 , ,1的卡片,
乙同学手中藏有三张分别标有数字1,3,2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
(1)请你用树形图或列表法列出所有可能的结果.
(2)现制定这样一个游戏规则:若所选出的a,b能使得
有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请你用概率知识解释.甲1乙132∴(a,b)取值结果共有9种 ∴P(甲获胜)= P(Δ>0)=
>P(乙获胜) =(2)
∵Δ=b2-4a与对应(1)中的结果为:-1、2、7、0、3、8、-3、0、5 所以不公平4. 小明和小刚玩“石头、剪刀、布”的游戏,每一局游戏双方各自随机做出“石头”、“剪刀”、“布”三种手势的一种,规定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,相同的手势是和局.(1)用树形图或列表法计算在一局游戏中两人获胜的概率各是多少?解:(1)画树状图得: ∵总共有9种情况,每一种出现的机会均等,每人获胜的情形都是3种, ∴两人获胜的概率都是(2)由(1)可知,一局游戏每人胜、负、和的机会均等,都为 ,任选其中一人的情形可画树状图得:∵总共有9种情况,每一种出现的机会均等,当出现(胜,胜)或(负,负)这两种情形时,赢家产生.∴两局游戏能确定赢家的概率为:4. 小明和小刚玩“石头、剪刀、布”的游戏,每一局游戏双方各自随机做出“石头”、“剪刀”、“布”三种手势的一种,规定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,相同的手势是和局.
(2)如果两人约定:只要谁率先胜两局,就成了游戏的赢家.
用树形图或列表法求只进行两局游戏便能确定赢家的概率. 本节课你学到了什么?课堂小结
同课章节目录
