浙教版九年级上册第1章 二次函数1.1 二次函数 课件
文档属性
| 名称 | 浙教版九年级上册第1章 二次函数1.1 二次函数 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-10 11:05:26 | ||
图片预览






文档简介
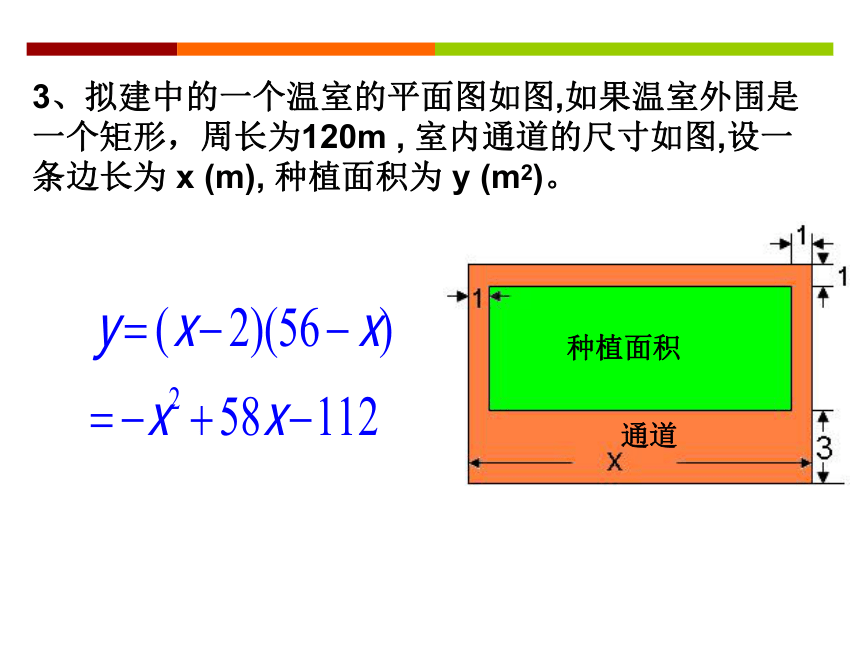
课件16张PPT。Q1:我们学过哪些函数?一次函数、正比例函数、反比例函数Q2:函数的定义是什么?在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地确定了一个y的值,那么我们称y是x的函数,其中x是自变量,y是因变量。1、有一根长12米的绳子,用它围成一个矩形,怎么样围能使这个矩形的面积达到最大?2、投篮时,篮球的运动路线是什么曲线?这两个问题,让我们在学习了本章二次函数之后,再来一起解答吧1.1 二次函数请用适当的函数解析式表示下列问题情境中的两个变量 y 与 X 之间的关系:1、圆的面积y (cm2)与圆的半径x (cm)。2、王先生存人银行2万元,先存一个一年定期,一年后银行将本息自动转存为又一个一年定期,设一年定期的年利率为x,两年后王先生共得本息y万元。3、拟建中的一个温室的平面图如图,如果温室外围是一个矩形,周长为120m , 室内通道的尺寸如图,设一条边长为 x (m), 种植面积为 y (m2)。上述函数解析式具有哪些共同的特征?经化简后都具有y=ax2+bx+c 的形式。一般的,我们把形如y=ax2+bx+c(其中a,b,c是常数,且a≠0)的函数叫做二次函数。a为二次项系数
b为一次项系数
c为常数项 做一做下列函数中,哪些是二次函数?y=x2y=2x2-x-1y=x(x-1)y=(x-1)2y=(x-1)2-(x-1)(x+1)说出下列二次函数的二次项系数、一次项系数和常数项: 试一试:二次函数y=ax2+bx+c中a≠0,但b、c可以为0。-158-112202-0.5130π00例1如图,矩形ABCD中,AB=6,BC=12,E为AB上一点,不与A、B重合,F为BC上一点,不与B、C重合,且BF=2BE。设BE=x,△DEF的面积为S。
求S关于x的函数解析式,并求出自变量x的取值范围。∵BE=x
∴AE=6-x,BF=2x,CF=12-2x
∵S△DEF=S矩形ABCD-S△ADE-S△BEF-S△CDF
∴S△DEF=12×6- ×12(6-x)- x·2x·6(12-2x)
=-x2+12x 由题意得,0用20米的篱笆围一个矩形的花圃(如图),设连墙的一边为x,矩形的面积为y。(2)当x=3时 练习1答:当x=3时,矩形的面积为42m2 。解:(1)由题意得花圃的长为(20-2x)m,则可得∴y关于x的函数关系解析式为y=2x2+20x(0 (2) 当x=3时,矩形的面积为多少?已知二次函数y=x2+bx-c,
当x=-1时,y=0;当x=3时,y=0, 求:(1)b、c的值; (2)当x=-2时,y的值解:(1)把x=-1,y=0;x=3,y=0,代入y=x2+bx-c(2)由(1)得y=x2-2x-3,
当x=-2时,
y=(-2)2-(-2)×2-3=5已知二次函数y=ax2+bx+3, 当x=2时,函数值为3, 当x= -2时, 函数值为2, 求这个二次函数的解析式.练习2课堂小结1、二次函数的概念:形如2、a为二次项系数、b为一次项系数、c为常数项3、用待定系数法求二次函数的解析式函数 (其中a、b、c为常数),当a、b、c满足什么条件时,
(1)它是二次函数;
(2)它是一次函数;
(3)它是正比例函数;当 时,是二次函数;当 时,是一次函数;当 时,是正比例函数;拓展提高函数 当m取何值时,
(1)它是二次函数?
(2)它是反比例函数?(1)若是二次函数,则 且
∴当 时,是二次函数。(2)若是反比例函数,则 且
∴当 时,是反比例函数。练习3
b为一次项系数
c为常数项 做一做下列函数中,哪些是二次函数?y=x2y=2x2-x-1y=x(x-1)y=(x-1)2y=(x-1)2-(x-1)(x+1)说出下列二次函数的二次项系数、一次项系数和常数项: 试一试:二次函数y=ax2+bx+c中a≠0,但b、c可以为0。-158-112202-0.5130π00例1如图,矩形ABCD中,AB=6,BC=12,E为AB上一点,不与A、B重合,F为BC上一点,不与B、C重合,且BF=2BE。设BE=x,△DEF的面积为S。
求S关于x的函数解析式,并求出自变量x的取值范围。∵BE=x
∴AE=6-x,BF=2x,CF=12-2x
∵S△DEF=S矩形ABCD-S△ADE-S△BEF-S△CDF
∴S△DEF=12×6- ×12(6-x)- x·2x·6(12-2x)
=-x2+12x 由题意得,0
当x=-1时,y=0;当x=3时,y=0, 求:(1)b、c的值; (2)当x=-2时,y的值解:(1)把x=-1,y=0;x=3,y=0,代入y=x2+bx-c(2)由(1)得y=x2-2x-3,
当x=-2时,
y=(-2)2-(-2)×2-3=5已知二次函数y=ax2+bx+3, 当x=2时,函数值为3, 当x= -2时, 函数值为2, 求这个二次函数的解析式.练习2课堂小结1、二次函数的概念:形如2、a为二次项系数、b为一次项系数、c为常数项3、用待定系数法求二次函数的解析式函数 (其中a、b、c为常数),当a、b、c满足什么条件时,
(1)它是二次函数;
(2)它是一次函数;
(3)它是正比例函数;当 时,是二次函数;当 时,是一次函数;当 时,是正比例函数;拓展提高函数 当m取何值时,
(1)它是二次函数?
(2)它是反比例函数?(1)若是二次函数,则 且
∴当 时,是二次函数。(2)若是反比例函数,则 且
∴当 时,是反比例函数。练习3
同课章节目录
