4.3相似三角形课件（公开课）

(共16张PPT)
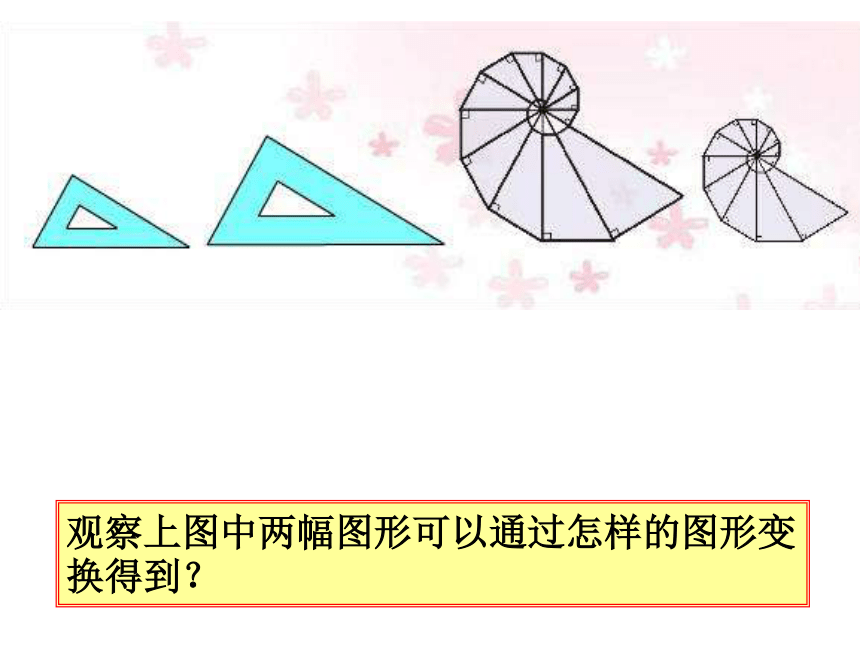
观察上图中两幅图形可以通过怎样的图形变换得到？
4.3 相似三角形
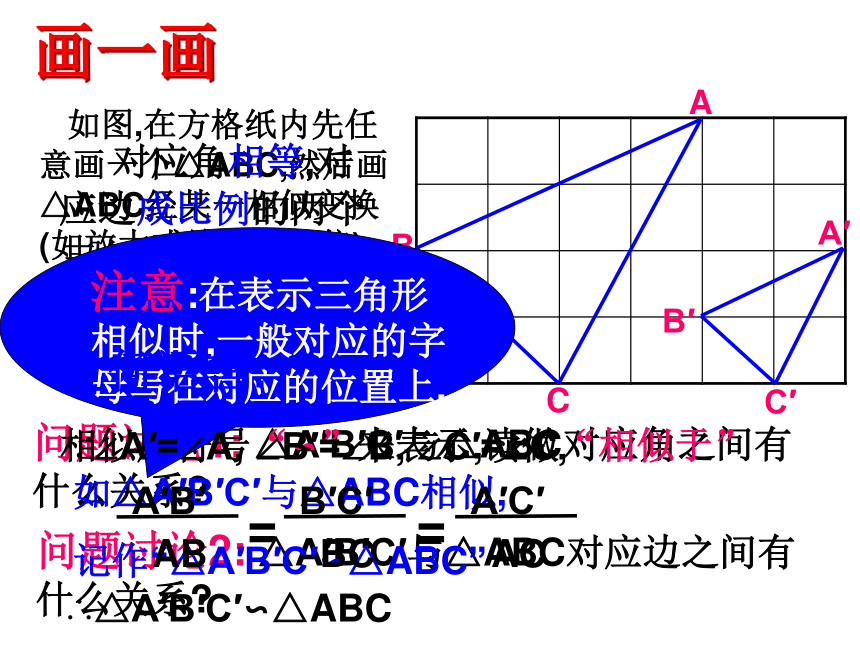
如图,在方格纸内先任意画一个△ABC,然后画△ABC经某一相似变换(如放大或缩小若干倍)后得到△A′B′C′(点A′,B′,C′分别对应点A,B,C,顶点在格点上).
问题讨论1: △A′B′C′与△ABC对应角之间有什么关系
问题讨论2: △A′B′C′与△ABC对应边之间有什么关系
C
A
B
B′
A′
C′
对应角相等,对应边成比例的两个三角形,叫做相似三角形.
相似用符号“∽”来表示,读做“相似于”
如△A′B′C′与△ABC相似,
记作“△A′B′C′∽△ABC”
注意:在表示三角形相似时,一般对应的字母写在对应的位置上.
几何语言:
∵∠A′=∠A, ∠B′=∠B, ∠C′=∠C,
AB
A′B′
BC
B′C′
AC
A′C′
=
=
∴△A′B′C′∽△ABC
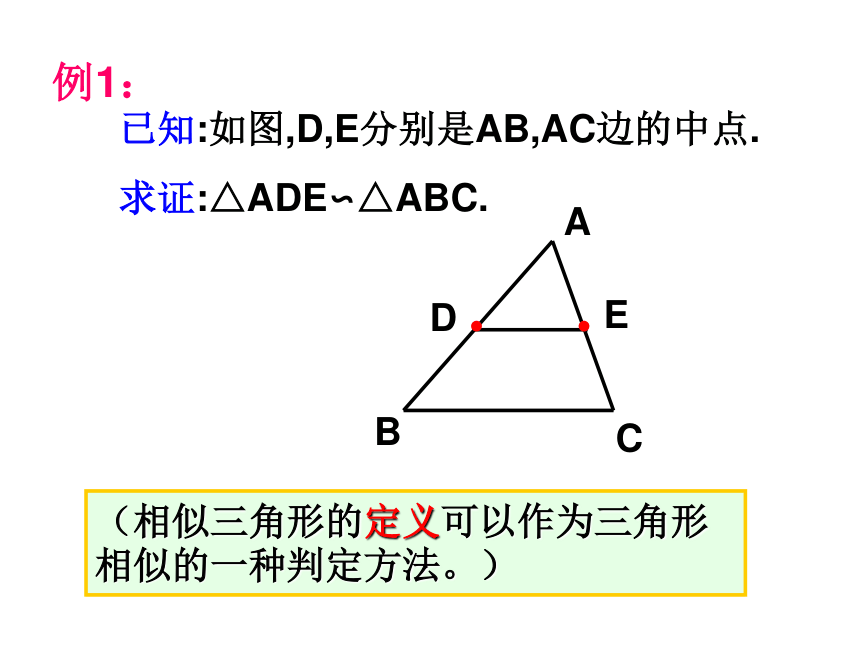
已知:如图,D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.
E
D
C
B
A
例1：
（相似三角形的定义可以作为三角形相似的一种判定方法。）
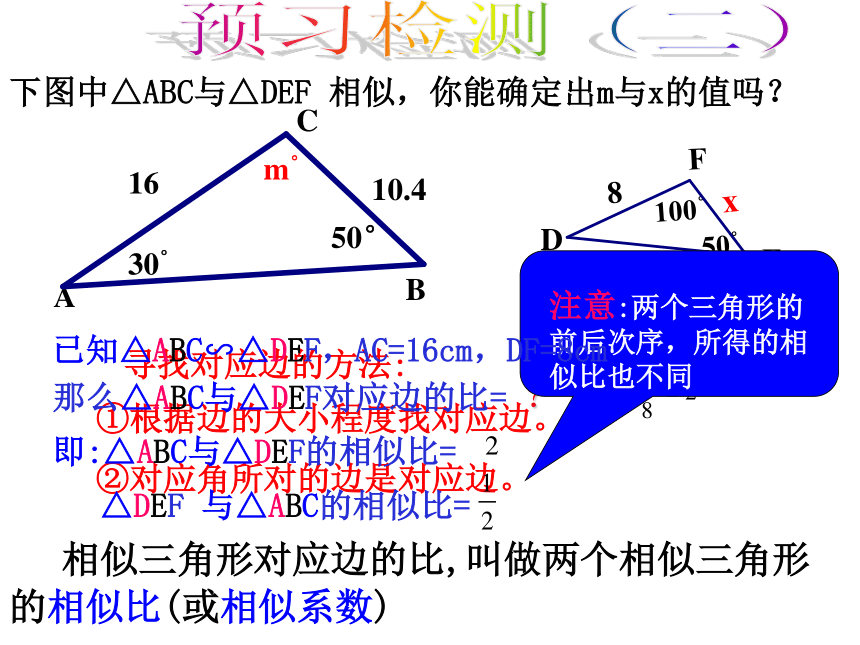
下图中△ABC与△DEF 相似，你能确定出m与x的值吗？
①根据边的大小程度找对应边。
②对应角所对的边是对应边。
30°
50°
16
10.4
A
B
C
m°
F
50°
100°
8
x
D
E
寻找对应边的方法:
那么△ABC与△DEF对应边的比= ？
相似三角形对应边的比,叫做两个相似三角形的相似比(或相似系数)
即:△ABC与△DEF的相似比=
△DEF 与△ABC的相似比=
注意:两个三角形的前后次序，所得的相似比也不同
已知△ABC∽△DEF，AC=16cm，DF=8cm
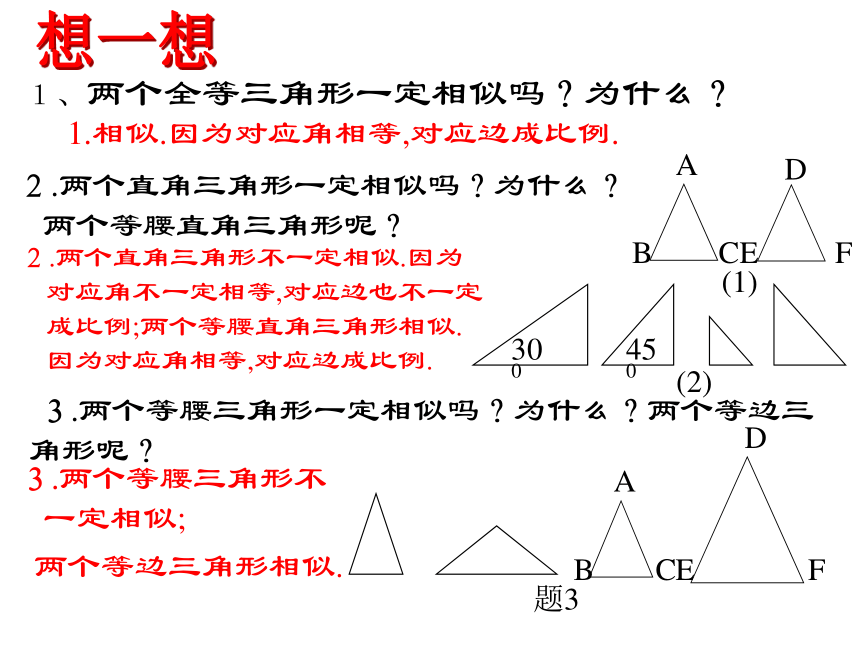
１、两个全等三角形一定相似吗？为什么？
２.两个直角三角形一定相似吗？为什么？两个等腰直角三角形呢？
３.两个等腰三角形一定相似吗？为什么？两个等边三角形呢？
(1)
B
C
D
E
F
A
题3
B
C
D
E
F
A
300
450
(2)
1.相似.因为对应角相等,对应边成比例.
２.两个直角三角形不一定相似.因为对应角不一定相等,对应边也不一定成比例;两个等腰直角三角形相似.因为对应角相等,对应边成比例.
３.两个等腰三角形不一定相似;
两个等边三角形相似.
为什么？
相似三角形的传递性：如果△ABC∽△A1B1C1 ，
而△A1B1C1 ∽△A2B2C2
那么△ABC∽△A2B2C2 。
如果△ABC∽△A1B1C1
而△A1B1C1 ∽△A2B2C2
那么△ABC与△A2B2C2
是否相似？
问题
例2、如图(1),D,E分别是△ABC的边BA, CA的延长线上的点, 点D与点B是对应点.△ADE ∽△ ABC。请你找到这两个三角形的对应角、对应边。
A
E
D
C
B
图1
已知AD﹕AB=1﹕2,BC=9cm,求DE的长.
变式1、如图(2),D,E分别是△ABC的边AB,AC上的点,点D与点B是对应点. △ ADE ∽△ ABC.请你找到这两个三角形的对应角、对应边。
A
D
E
B
C
图2
已知AD﹕DB=1﹕2,BC=9cm,求DE的长。
变式2：如图(3),D,E分别是△ABC的AB,AC边上的点，△ADE∽△ACB.∠ADE＝∠C
A
D
E
B
C
图3
AD＝2 cm,DB＝4 cm,AC＝10cm,求AE的长.
变式3、如图(4),D是△ABC的边AB上的点,
△ ACD ∽△ ABC. ∠ACD＝∠B
已知:AD＝9 cm, BD＝7cm,求AC的长.
图4
变式4、如图(5),D、E分别是△ABC的边BA、CA延长线上的点, 点D与点C是对应点. △ ADE ∽△ ACB.
AD＝2 cm,AB＝6 cm,AC＝ 4 cm,求AE的长.
A
D
E
B
C
图5
2、如图，AB，CD相交于点0, △AOC∽ △BOD 。
（1）如果OC：OD＝1：2,AC＝5,求BD的长；
（2）如果∠A＝35°, ∠AOC＝100°,求∠D的度数。
C
B
O
A
D
第2题
堂堂清练习：
如图,D是AB上一点, △ABC∽△ACD,且AD:AC=2:3, AD=4,∠ADC=65°, ∠B=43°
(1)求∠ACB, ∠ACD的度数;
(2求AB的长.
65°
43°
已知△ABC与△DEF相似, △ABC的三边为2,3,4, △DEF的最大边为8,求其余两边.
已知△ABC与△DEF相似, △ABC的三边为2,3,4, △DEF的一边为8,求其余两边.
4,6
4,6或12,16或16/3,32/3
梳理知识
利用相似三角形的性质来计算三角形的对应角、对应边。
对应角
对应边
记法
定义
对应角相等、对应边相等的两个三角形叫做全等三角形。
对应角相等
对应边相等
△ABC≌DEF
对应边成比例
对应角相等
对应角相等、对应边成比例的两个三角形叫做相似三角形
△ABC ∽ DEF
全等三角形是相似三角形的特殊情形（相似比为1）
相似三角形