3.1（1）直线与圆的位置关系

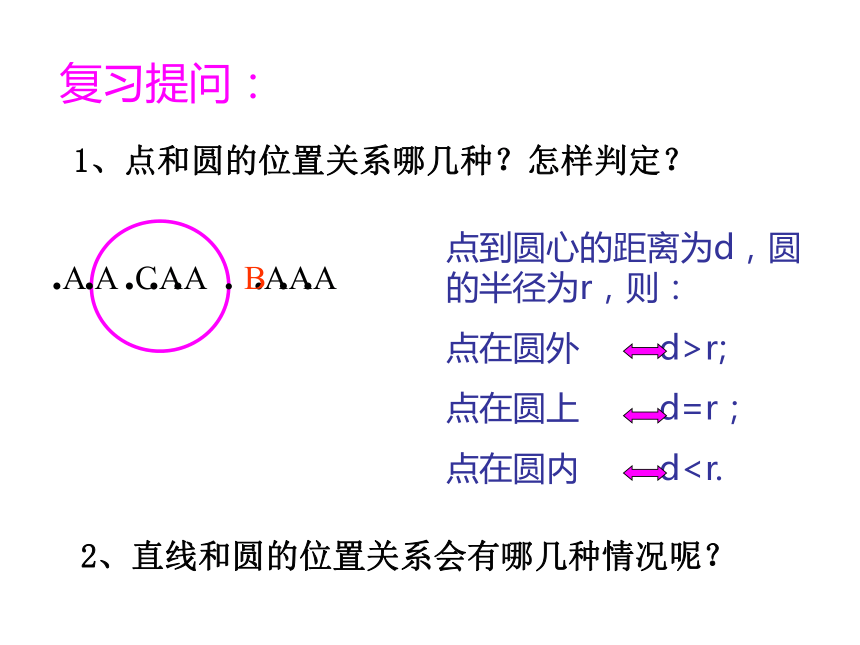
课件26张PPT。复习提问：1、点和圆的位置关系哪几种？怎样判定？.A.A.A . B.A.A.C.A.A点到圆心的距离为d，圆的半径为r，则：
点在圆外 d>r;
点在圆上 d=r；
点在圆内 d 如果把地平线看作一条直线，太阳看作一个圆，在“日落”过程中我们可以发现直线与圆有着不同位置关系. 海平面3.1 直线和圆的位置关系探索直线与圆有几种位置关系?
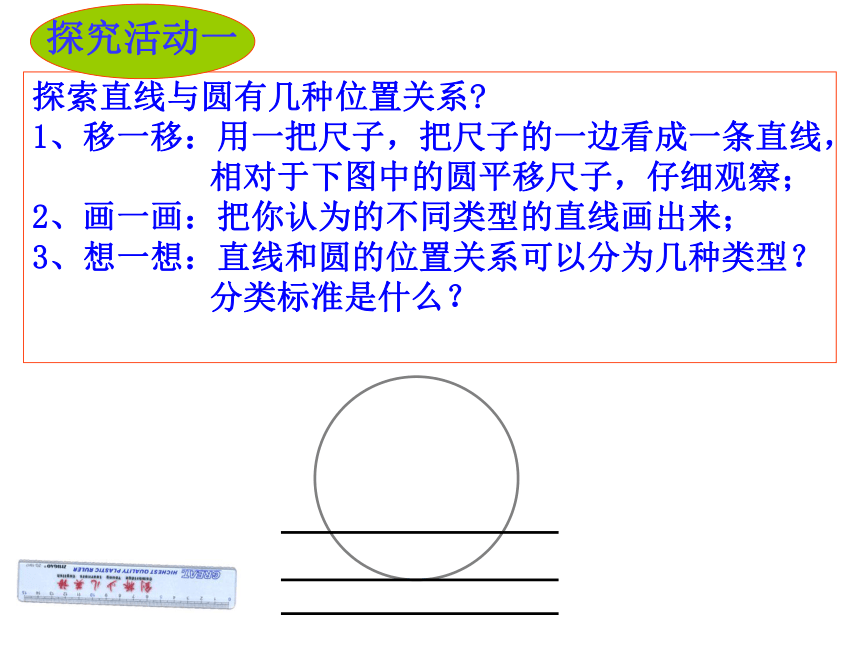
1、移一移：用一把尺子，把尺子的一边看成一条直线，相对于下图中的圆平移尺子，仔细观察；
2、画一画：把你认为的不同类型的直线画出来；
3、想一想：直线和圆的位置关系可以分为几种类型？分类标准是什么？直线和圆没有公共点时,叫做直线与圆相离.直线和圆有唯一公共点时,叫做直线与圆相切.直线和圆有两个公共点时,叫做直线与圆相交. 这时直线叫做圆的切线 ,
唯一公共点叫做直线与圆的切点.
直线与圆的位置关系用数学的眼光看生活用数学的眼光看生活用数学的眼光看生活辨真伪，说理由：（1）当直线和圆相离时，直线和圆一定没有公共点。（ ） √×（3）过⊙O内一点P作直线l,则直线l与⊙O相交。（ ）（4）过⊙O外一点P作直线l，则直线l与⊙O相切或相交。（ ）（5）过⊙O上一点p作直线l，则直线l与⊙O相切。（ ）（2）直线和圆有公共点时叫做直线和圆相切. （ ）√××运用：1、看图判断直线l与 ⊙O的位置关系（1）（2）（3）（4）（5）相离相切相交相交？lllll·O·O·O·O·O（5）？l 如果，公共点的个数不好判断，该怎么办？·O “直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析？·
A·
B1、过⊙O内一点P作直线l,则直线l与⊙O的位置关系是______
过⊙O上一点P作直线l,则直线l与⊙O的位置关系是______
过⊙O外一点P呢？_________________相交相交、相切或相离相切或相交如图.O为直线L外一点，OT⊥L，且OT=d.请以O为圆心，分别以 为半径画圆.所画的圆与直线L有什么位置关系?做一做直线与圆的位置关系d>r ，那么直线l与⊙O相离d=r ，那么直线l与⊙O相切dAB= = =5即 圆心C到AB的距离d=2.4cm
解：过C作CD⊥AB，垂足为D，则 在△ABC 中，∠ACB=90°，AC=3cm，BC=4cm，设⊙C的半径为r，请根据r的下列值，判断AB与⊙C的位置关系，并说明理由。(1) r = 2cm（2）r =2.4cm（3）r =３cm 考考你在Rt△ABC中，根据三角形的面积公式有ABCD3cm4cm(1) r = 2（2）r =2.4ABCD3cm4cm（３）r =３ABCD3cm4cm当r =2cm时，
d > r，
∴☉C 与
直线AB相离； 当r =2.4cm时，
d = r，
∴☉C 与直线AB相切； 当r =3cm时，
d < r，
∴☉C 与直线AB相交。2.4cm2.4cm2.4cm 在△ABC 中，∠ACB=90°，AC=3cm，BC=4cm，设⊙C的半径为r。比一比1、当r满足________________时，
⊙C与直线AB相离． 2、当r满足____________ 时，
⊙C与直线AB相切． r＜2.4cmr=2.4cmABCD3cm4cm2.4cm3、当r满足____________时，
⊙C与直线AB相交．r＞2.4cm4、当r满足_______________ 时,
⊙C与线段AB只有一个公共点.0cm<在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，r为半径作圆。想一想
?? 当r满足___________
_____________ 时,⊙C与线段AB只有一个公共点.r=2.4cmBCAD453 或3cm<≤4cm 例. 在码头A的北偏东60°方向有一个海岛，离该岛中心P的12海里范围内是一个暗礁区。货船从码头A由西向东方向航行，行驶了10海里到达B，这时岛中心P在北偏东45°方向。若货船不改变航向，问货船会不会进入暗礁区？用一用例. 在码头A的北偏东60°方向有一个海岛，离该岛中心P的12海里范围内是一个暗礁区。货船从码头A由西向东方向航行，行驶了10海里到达B，这时岛中心P在北偏东45°方向。若货船不改变航向，问货船会不会进入暗礁区？解:如图,作PH⊥AB,垂足为H.则∠PAH=30°∠PBH=45°，∴货船不会进入暗礁区H45°∵AH-BH=AB=10∵13.66＞12┏小结：0d>r1d=r切点切线2d 的个数来判断；（2）根据性质，由_______________________________的关系来判断．在实际应用中，常采用第二种方法判定．两直线与圆的公共点圆心到直线的距离d与半径r3、常用的辅助线是：圆心到直线的_______________垂线段再见