5.5平行四边形的判定(1)

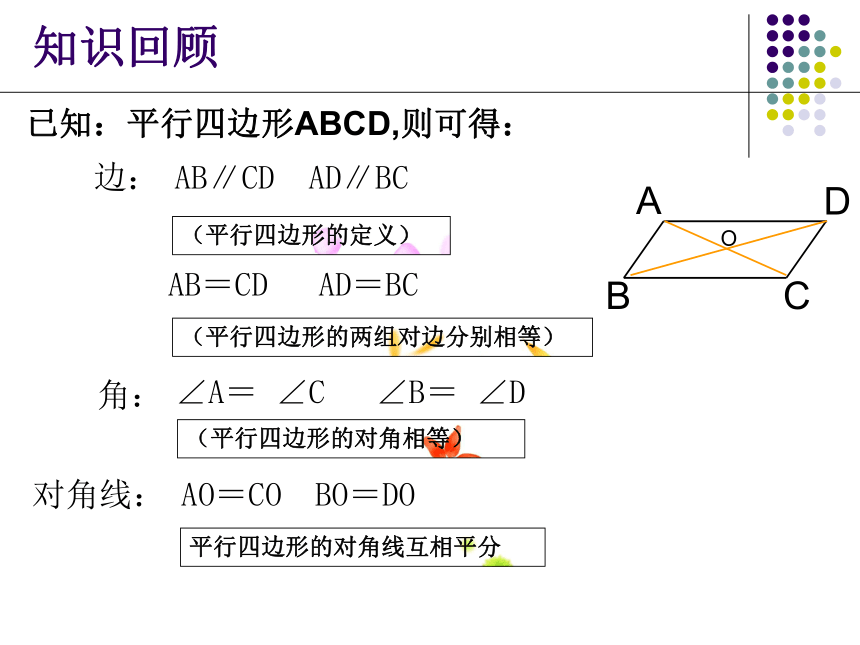
课件15张PPT。数学5.5 平行四边形的判定(1)已知：平行四边形ABCD,则可得：边：角：对角线：AB＝CD　 AD＝BCAB∥CD　AD∥BC
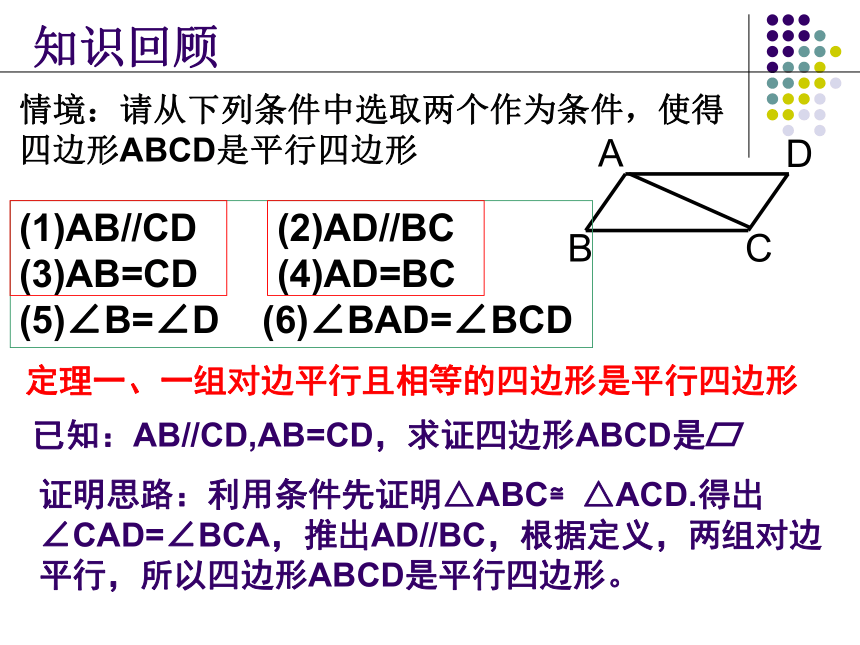
（平行四边形的定义）（平行四边形的两组对边分别相等）（平行四边形的对角相等）∠A＝ ∠C　 ∠B＝ ∠DAO＝CO　BO＝DO平行四边形的对角线互相平分知识回顾情境：请从下列条件中选取两个作为条件，使得
四边形ABCD是平行四边形知识回顾(1)AB//CD (2)AD//BC
(3)AB=CD (4)AD=BC
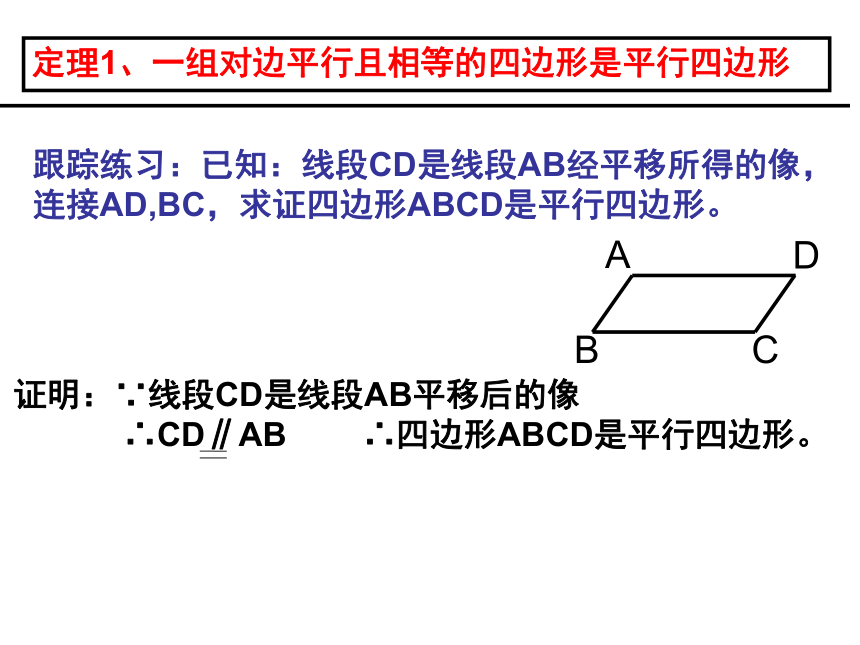
(5)∠B=∠D (6)∠BAD=∠BCD定理一、一组对边平行且相等的四边形是平行四边形已知：AB//CD,AB=CD，求证四边形ABCD是证明思路：利用条件先证明△ABC≌△ACD.得出∠CAD=∠BCA，推出AD//BC，根据定义，两组对边平行，所以四边形ABCD是平行四边形。定理1、一组对边平行且相等的四边形是平行四边形跟踪练习：已知：线段CD是线段AB经平移所得的像，连接AD,BC，求证四边形ABCD是平行四边形。证明：∵线段CD是线段AB平移后的像
∴CD∥AB ∴四边形ABCD是平行四边形。 情境：请从下列条件中选取两个作为条件，使得
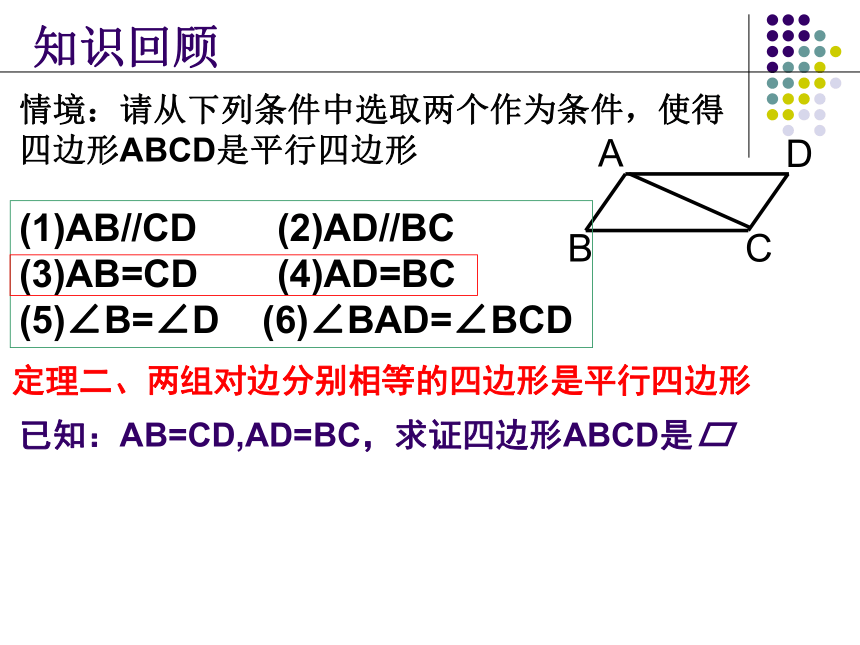
四边形ABCD是平行四边形知识回顾(1)AB//CD (2)AD//BC
(3)AB=CD (4)AD=BC
(5)∠B=∠D (6)∠BAD=∠BCD定理二、两组对边分别相等的四边形是平行四边形已知：AB=CD,AD=BC，求证四边形ABCD是定理2、两组对边分别相等的四边形是平行四边形跟踪练习：已知：线段AB,BC是平行四边形ABCD的两条邻边，请补充图形。根据定义：两组对边分别平行的四边形叫做平行四边形.
定理1 一组对边平行且相等的四边形是平行四边形.
定理2 两组对边分别相等的四边形是平行四边形.概念与定理平行四边形的判定方法:疑问举反例说明老师提示:举反例证明假命题千万不可忘记噢!一组对边平行，另一组对边相等的四边形是否一定是平行四边形？在四边形ABED中,可知AB=DE且AD∥BE,
但该四边形显然不是平行四边形,而是等腰梯形.ＤＡＢ已知：如图，在 ABCD中，E，F分别是边AB，
CD的中点.求证：EF//AD//BC.变式练习：
如图，在 ABCD中，若
AE：BE＝1：2，DF：CF＝1：2
求证：EF//AD//BC.例1 学以致用1.已知：如图，E,F分别是 的边AD,BC的中点。求证：BE=DF.D证明：∵四边形ABCD是平行四边形，∴AB∥CD (平行四边形的定义)AD=BC(平行四边形的对边分别相等)，∵E,F分别是AD,BC的中点，∴四边形EBFD是平行四边形（一组对边 平行并且相等的四边形是平行四边形）。∴BE=DF(平行四边形的对边分别相等)。课内练习1学以致用已知：如图，在△ABC中，AB=AC,点P是BC上一点，且PE//AC,PF//AB，问线段PE,PF,AB三者之间的数量关系。A课内练习2学以致用BCPEF已知：如图，在 ABCD中，E，F分别是AB，CD的中点，分别延长BA,DC于G,H,使得AG=CH.求证：GF//EHA课内练习3学以致用BCGEFDH直角坐标系内有平行四边形的三个顶点，它们的坐标分别是A（2，1）、B（-1，-2）、C（3 , -2 ），试找出第四个顶点的位置，并写出它的坐标。拓展与提高勇攀高峰太棒了！直角坐标系内四边形ABCD的四个顶点坐标分别为
A(-3，-2)、B(0,3)、C(3,2)，D(0,-3)
那么四边形ABCD是否平行四边形。拓展与提高勇攀高峰小结根据定义：两组对边分别平行的四边形叫做平行四边形.
定理1 一组对边平行且相等的四边形是平行四边形.
定理2 两组对边分别相等的四边形是平行四边形.
……平行四边形的判定方法: